Omni-directional damage detection and localization with a 2-D piezoelectric ultrasonic phased array

2.1. Cross-shaped array signal model

The layout of the cross-shaped array is as illustrated in Fig. 1. Two linear piezoelectric transducer (PZT) arrays labeled No. 1 and No. 2, consist of $M$ and $N$ PZT elements with inter-element spacing of $d_x$ and $d_y$ respectively, are aligned along the $x$ and $y$ axes, with the mid-point of each array meeting at the axes’ origin. For a distant point $P(\mathbf{r},\theta )$, $\mathbf{r}$ refers to the vector spanning from the origin topoint $P$. Because $d_x$, $d_y\ll r$ ($r=\left|\mathbf{r}\right|$), the rays connecting point $P$ and each of the respective sensors can be assumed to be parallel with each other, inclined at angle $\theta$.

Fig. 1Cross-shaped array

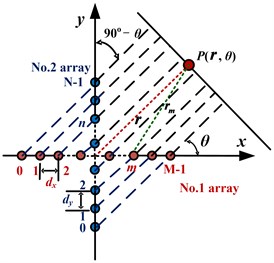
It is assumed that each PZT element of the cross-shaped array is excited and Lamb waves generated on the plate will reach point $P$. The synthetic signal $S_P$ can be broken down into signal components that excited all the piezoelectric patches of No. 1 and No. 2 arrays, denoted by $S_{Px}$ and $S_{Py}$ respectively.

For the far field case, ${\mathbf{r}}_m=\mathbf{r}$, ${\mathbf{\xi }}_m=\mathbf{\xi }={\mathbf{r}}_m\mathit{}/\left|{\mathit{r}}_m\right|$. If the weights are chosen as unity, $w_m=$1, and thus the synthetic wave front that reaches $P$, propagating from the total of $M$ PZT elements of the No. 1 array can be represented by:

where $\omega$ is wave frequency, $c$ is the Lamb wave velocity on the structure.

To steer the output wave front $S_{Px}(\mathbf{r},t)$ into a certain ${\varphi }_0$ direction, the delays $\mathrm{\Delta }m\left({\varphi }_0\right)$ are introduced. Eq. (1) becomes:

Similarly for $S_{Py}(\mathbf{r},t)$, the delays $\mathrm{\Delta }n\left({\varphi }_0\right)$ are introduced:

If the time delay is chosen as shown by Eqs. (4) and (5), the maximum of the beam forming factor can be achieved, and the synthetic signal $S_{Px}\left(\mathbf{r},t\right)$ will be strengthened by $M$ times with respect to the individual reference signal $f(t-r/c)$. Likewise, the synthetic signal $S_{Py}\left(\mathbf{r},t\right)$ will then be $N$ times the individual reference signal $f(t-r/c)$. The resulting forms of the synthetic signals are presented as in Eqs. (6) and (7):

Hence, the overall synthetic signal of cross-shaped array can be expressed as:

Based on the principle of reciprocity, the receiving process must be consistent with the exciting process, given that the same conditions apply within the two processes. Therefore, according to the stated principle, let’s say that the excited signals left the PZT elements within a set of specific time delays, the returning signals should be able to arrive at all the PZT elements at the same time:

2.2. Damage localization

When the signal beam points at the direction towards the damage location, all signals will be focused, and the energy of combined signal will be enhanced. Subsequently, the signal energy reflected by damage is also the strongest in this direction. Information related to the damage angle can thus be obtained according to this principle. By analyzing the signal in the damage direction, the damage distance r can be calculated as:

where $t$ is the time of arrival of the signal in the damage direction.

2.3. Image enhancement

The scan images can be obtained by displaying the energy of synthetic signal from all directions on the polar coordinate plane in a gray level resolution. The appearance of phantom images in the opposite side of cross-shaped array synthetic signal will affect the result of damage localization, especially for the case of multiple damages. An image enhancement method is proposed in order to make the damage scan image clearer. The synthetic signals is firstly normalized, and then the exponential function algorithm is taken into account. The function is shown below:

where $S$ is the amplitude of the synthetic signals before optimization, $S_1$ is the corresponding synthetic signal amplitude after the optimization. $k$ is the power of exponential function, which is equivalent to the size of the control value of the original image used to enhance the contrast of the gray value of each part.

3.1. The experimental system

It can be seen from Fig. 2(a) that the experimental setup consists of an aluminum plate, a cross-shaped PZT array and a multi-channel scanning systems developed by Nanjing University of Aeronautics and Astronautics laboratory [15]. The dimension of the aluminum plate is 1000 mm×1000 mm×2 mm, whereas the diameter and thickness of each of the PZT elements are 8 mm and 0.48 mm respectively. Each of the linear arrays of the cross-shaped PZT array is made up of seven PZT elements with a 9 mm spacing between two adjacent elements. The PZT elements for both linear arrays are labeled as PZT0 to PZT6. PZT3, being the mutual element, and also the center point of both linear arrays in this case, is set as the coordinate’s origin. A 2 kg weight with a diameter of 20 mm is used to simulate the damage.

Fig. 2Experiment setup and the damages position (unit: mm)

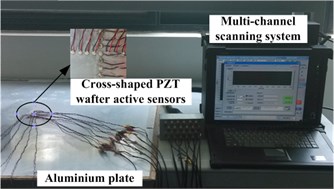
a) Experimental setup

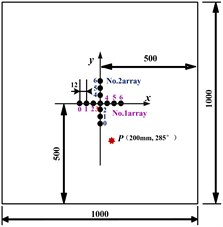
b) Single damage position

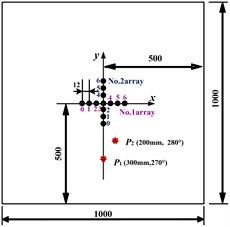
c) Multiple damages position

3.2. Single damage detection and localization

The excitation signal is the modulate five-cycle sine burst, while the excitation frequency is set at 40 kHz where $A_0$ mode sensor signal amplitude dominates that of the $S_0$ mode, which is believed to be conducive to the signals’ analysis. The sampling frequency is set at 2 MHz, and 1300 points are collected.

The positions of the damage and the PZT elements are as shown in Fig. 2(b). Actual damage point $P$ (200 mm, 285°) is adopted. Data collection is conducted in a round-robin pattern. In each turn, one element plays the role of a transmitter and sends out excitation while the rest serve as receivers and pick up the reflections of both arrays. All the elements in the array take turns to serve as transmitters. The received signals in the health status and the damage status are called the health and damage signals respectively. The differential signals between the health and damage signals are called damage reflection signals, which are delayed and superimposed according to the beam angle delay formula to obtain the synthetic damage reflection signal.

It can be found that when the maximum synthetic signal is directed at the actual damage angle of 285°, a mirrored synthetic signal shows up symmetrically at 75°, as shown in Fig. 3(a). It is proved that when there is only one working linear array, in this case, the No.1 array, a phantom image will also appear on the scan image. This phenomenon of inherent mirror symmetry subsequently results in the inspection area being limited to, at most, 180°.

Likewise, from what can be seen in Fig. 3(b), if only the No. 2 array is used to detect damage, problems will also occur. In this case, since the 285° damage angle is located very close to the array (or the $y$-axis), not only that a phantom image is seen, but it also appears to be connected to the image of the actual damage, which makes it more difficult to identify the actual damage location. Then, the fusion of two linear arrays’ signal detection algorithm is adopted. It was found that the resulting scan image displays the superposition of the the two problematic linear arrays’ scan image, as can be seen in Fig. 3(c).

Fig. 3Damage detection figure

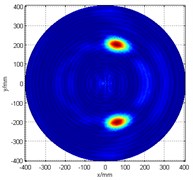
a) No. 1 array only

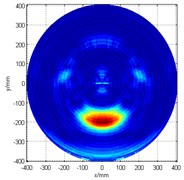
b) No. 2 array only

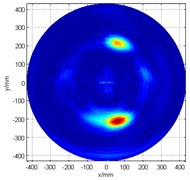
c)The original image

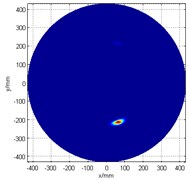
d) The image after enhancement

In order to reduce the effect of the unwanted phantom image as well as to improve the damage recognition quality, an image enhancement method is applied to optimize the image by setting the exponential power $k$ in Eq. (11) to 5. The enhanced damage scan image is shown in Fig. 3(d). The detection result is $P$ (210 mm, 287°), with an angular error of 2°, and positional error of less than 1 cm (actual damage location is $P$ (200 mm, 285°)). This result proved that the combination of the cross-shaped ultrasonic phased array and image enhancement method can effectively identify the structural damage.

3.3. Multiple-damage detection and localization

The combination of the cross-shaped ultrasonic phased array and the image enhancement method can also be used for multiple damages identification. Its principle and recognition process is similar to that of the singular damage identification. The damage positions and the layout of the piezoelectric elements are shown in Fig. 2(c). The actual damage points are $P_1$ (300 mm, 270°) and $P_2$ (200 mm, 280°).

Fig. 4Multiple-damage detection figure

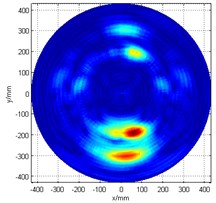
a) The original image of cross-shaped array

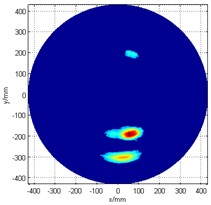
b) The image after enhancement

The pre-enhanced cross-shaped array damage scan image is as shown in Fig. 4(a). This time, a smaller power of exponential function was chosen to help ease the detection of damage $P_1$, since its energy is not so strong. A threshold setting (60 % of the maximum value of the synthetic signal) was firstly applied, and then for the image enhancement processing, the exponential power $k$ is set to 2. Fig. 4(b) presents the post-enhancement damage detection scan image. The damage detection results are $P_1$ (210 mm, 273°) and $P_2$ (195 mm, 284°), which means that the angular error is less 4°, and the positional error is less than 2 cm when compared to the actual damage $P_1$ (300 mm, 270°) and $P_2$ (200 mm, 280°).