Fractional derivative method to reduce noise and improve SNR for lamb wave signals

1. Introduction

A Lamb wave is a type of elastic stress waves propagating in the free boundary plate combining the transverse and longitudinal waves propagating in two parallel surfaces of the plate. In comparison with the bulk wave scanning method, the Lamb wave method has some advantages in structural health monitoring, such as the long spreading distance along the structure [1-4]. The experimental Lamb wave signal is complex in the actual environment because of the effect of different levels of noises that impact the detecting accuracy. Therefore, methods of noise reduction for Lamb wave signals are clearly desired.

There have been many studies regarding noise reduction for ultrasonic Lamb wave signals – mainly the empirical mode decomposition (EMD) method and the wavelet transform (WT) method [5-14]. The WT method is used in nondestructive testing due to its advantage in signal denoising. For example, Siqueira processed Lamb wave signals using the discrete WT with fixed threshold value [7]. Marchi used the warped WT to process multi-mode Lamb waves [8]. Matz evaluated the various WT techniques by the signal-to-noise ratio enhancement [9]. Liang used the optimal scale WT to identify the weak signal [10]. Pardo dealt with the grain noise reduction by using the undecimated WT [11]. However, the fixed threshold and soft threshold both have their own disadvantages. The performance of the WT method depends on the wavelet basis [12]. The EMD method can reduce noises adaptively according to the Lamb wave signal features; however, it cannot reduce noise completely, leaving noises in the rebuilt signals [13, 14].

Lamb wave signals have dispersive and multi-modal characteristics. The single mode Lamb wave signal could be excited by selecting the frequency bandwidth of the piezoelectric transducer [15]. Therefore, the signal of the single mode dispersive Lamb wave is processed in this paper.

To further study the noise reduction and signal-to-noise ratio (SNR) improvement method and improve the detecting accuracy, this paper presents a noise reduction method for Lamb wave signals based on the fractional derivative theory. Both the simulated and experimental data are used to evaluate this method both qualitatively and quantitatively. The Lamb wave signal method is also compared with the EMD method and the WT method to demonstrate its validity.

2. Method

The method mainly consists of three steps. First, the fractional derivative of the amplitude spectrum of the Lamb signal with noises at different derivative orders is obtained. Next, the characteristic parameters of the amplitude spectrum are calculated according to the proposed relationship between the peak amplitude and the derivative order as well as the relationship between the peak frequency and the derivative order. Finally, the Lamb wave signal without the various forms of noise is rebuilt by combining the amplitude and phase spectra.

Supposed a Lamb wave signal with the Gaussian envelope is $f\left(t\right)$, its amplitude spectrum $F\left(\omega \right)$ after the Fourier transform is:

where $t$ is the time, $\omega$ is the angular frequency, $\sigma$ is the peak width, $\mu$ is the peak position, and $A$ is the peak amplitude.

The fractional derivative $y\left(v\right)$ of the amplitude spectrum $F\left(\omega \right)$ is [16]:

where:

where $v$ is the derivative order, $h$ is the discrete step, $c$ is an initial value of $\omega$, and $⌊(\omega -c)/h⌋$ is the integer part of $(\omega -c)/h$.

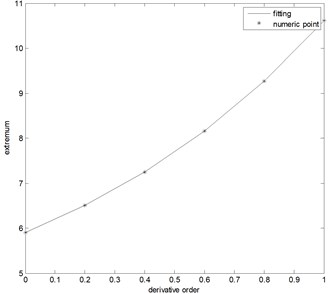
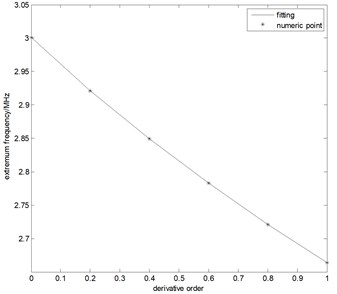
The fractional derivative functions of $F\left(\omega \right)$ at different derivative orders are shown in Fig. 1 when A is 5, $\mu$ is 3, and $\sigma$ is 0.33. The extremum $F_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and its corresponding frequency $f_m$ of the fractional differential functions change as the derivative order changes. The relationship between the extremum and the derivative order as well as that between the extremum frequency and the derivative order is quartic polynomial as shown in Figs. 2(a) and 2(b) when the derivative order is between 0 and 1. Their functions are:

where $c_0$, $c_1$, $c_2$, $c_3$, and $c_4$ are the coefficients of the quartic polynomial between the extremum and the derivative order; $d_0$, $d_1$, $d_2$, $d_3$, and $d_4$ are the coefficients of the quartic polynomial between the extremum frequency and the derivative order.

After the extremum and the extremum frequency curves are fit according to Eq. (4), their coefficients are calculated by means of the numeric method. By combining these coefficients with Eq. (1), the characteristic parameters of the amplitude spectrum, $\sigma$, $\mu$, and $A$, can be deduced. Because the signal-to-noise ratio reduces with the increase of the derivative order, we used a low order derivative from 0 to 1 to calculate the parameters. The expressions of the parameters can be written as:

After characteristic parameters, $\sigma$, $\mu$ and $A$, are obtained, the amplitude spectrum can be extracted. By combining the amplitude spectrum with the phase spectrum of the original signal, the Lamb wave signal without noises is rebuilt through the inverse Fourier transform.

Fig. 1The fractional derivative functions at different orders

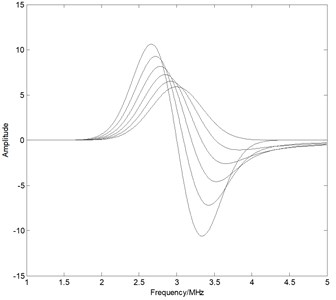
Fig. 2a) The extremum and b) the corresponding frequency at different derivative orders

a)

b)

3. Simulation test

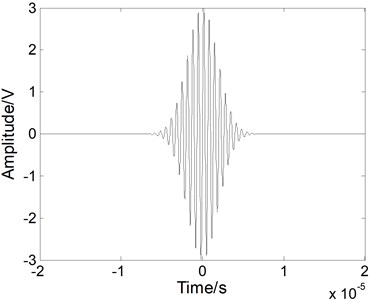
The noise reduction performance of the fractional derivative method is firstly verified using the simulated Lamb wave signal. A noise reduction process of a simulated Lamb signal [17, 18] was conducted and compared with the EMD method and the WT method. The WT method selects sys8 wavelet with the decomposition level 4. The simulated excitation signal is at a 2 MHz center frequency, as shown in Fig. 3(a). If an $S_0$ mode Lamb wave signal is excited in a 2 mm thickness steel plate, the simulated Lamb wave signal at a propagating distance of 100 mm can be written as [17]:

which is shown in Fig. 3(b). Here $x$ is the propagation distance and $c_p$ is the phase velocity of Lamb wave. Its duration becomes longer and its amplitude becomes lower in the time domain because of the dispersion effect.

Fig. 3a) The excitation signal and b) the simulated S0 mode Lamb wave signal at a propagating distance of 100 mm

a)

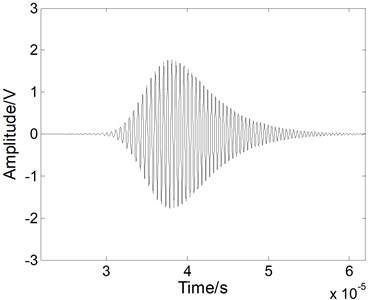
b)

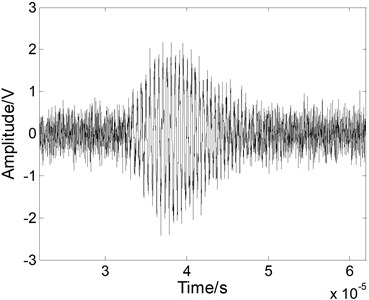
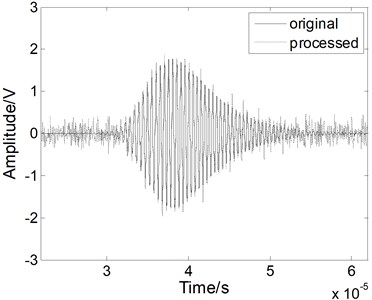
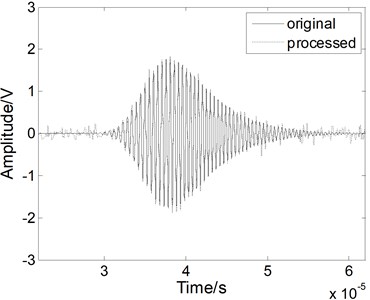
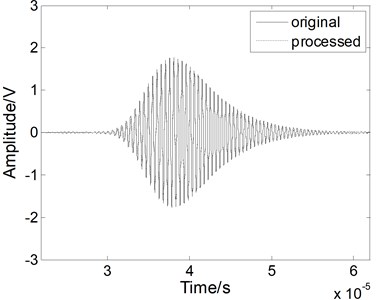
Fig. 4The Lamb wave signal: a) containing white noises, b) after EMD processing, c) after WT processing, and d) after fractional derivative processing when the SNR is 5 dB

a)

b)

c)

d)

A white noise with the SNR of 5 dB was mixed into the Lamb signal in the time domain, as shown in Fig. 4(a). In the time domain, we compared the method with the others. As shown in Fig. 4(b), when we use the EMD method, the noises cannot be eliminated effectively and the processed signal contains various forms of noise. As shown in Fig. 4(c), when we use the WT method, the performance of the noise reduction is improved compared to the EMD method, but the signal has some apparent distortions. When we use the fractional derivative method, both the signal is restored better than for the other methods, as shown in Fig. 4(d). Most of noises can be removed without burr. Above all, the fractional derivative method has the best noise reduction performance for the Lamb wave signal.

The noise reduction performance of the fractional derivative method is also verified using a simulated weak Lamb wave signal. The simulated weak Lamb signal with a SNR of 0 dB is shown in Fig. 5(a). The signal is completely masked by the noises. As shown in Figs. 5(b) and 5(c), when we use the EMD method and the WT method, the noises cannot be eliminated effectively and the processed signal still contains various forms of noise. The original weak signal is masked by the noises, even after the EMD or WT processing. When we use the fractional derivative method, both the main pulse signal and the small signal are restored better than in the case of the other methods, as shown in Fig. 5(d). Almost all of noise can be removed without burr. Therefore, the fractional derivative method has the best noise reduction performance for the weak Lamb wave signal.

Fig. 5The Lamb wave signal: a) containing noises, b) after EMD processing, c) after WT processing, and d) after fractional derivative processing when the SNR is 0 dB

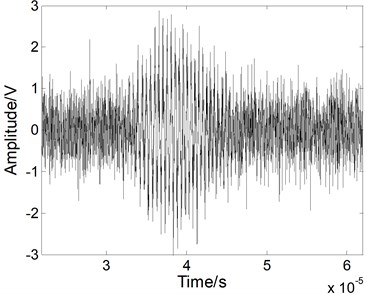
a)

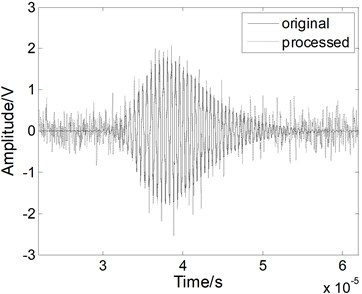
b)

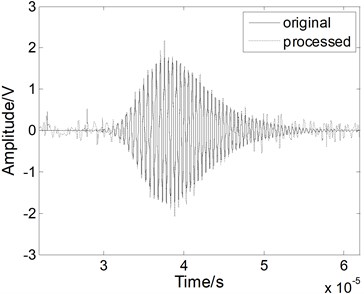
c)

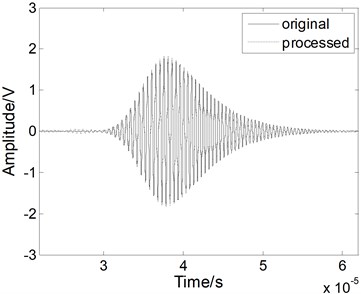
d)

To evaluate the noise reduction performance quantitatively, two performance parameters, i.e., signal-to-noise ratio (SNR) and the mean square error (MSE), are used. Comparisons of the evaluation parameters with the above three methods when the SNR is 5 dB and 0 dB are presented in Tables 1 and 2. As summarized in those tables, after comparing with the results of the EMD method and the WT method, the fractional derivative method can reduce the MSE and improve the SNR of the processed signal. Relative to those of the EMD method, the SNR is improved by 23 dB and the MSE is reduced by approximately 13 dB. Relative to those of the WT method, the SNR is improved by approximately 10 dB and the MSE is reduced by approximately 10 dB. Briefly, the fractional derivative method has the best noise reduction performance for the Lamb wave signal among the three methods.

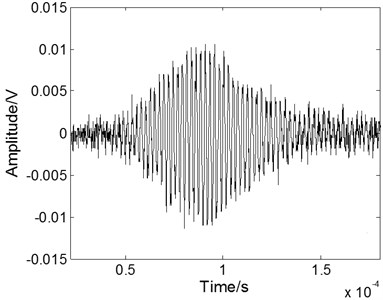
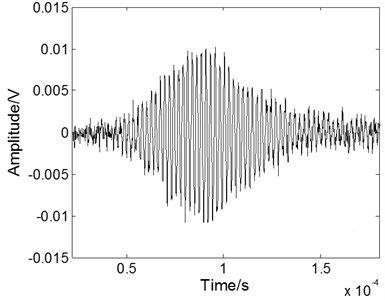
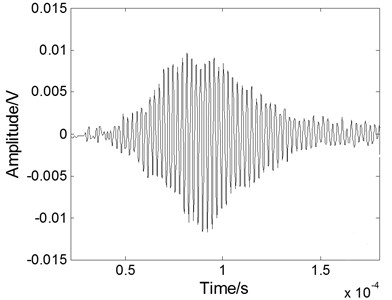
Fig. 6The experimental Lamb wave signal: a) containing noises, b) after WT processing, c) after EMD processing, and d) after fractional derivative processing

a)

b)

c)

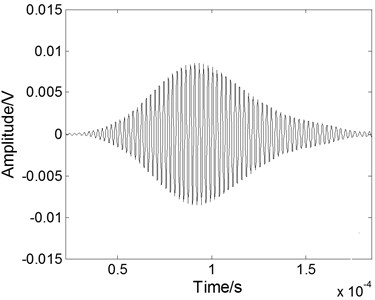
d)

4. Experimental results and discussion

To evaluate the performance of the fractional derivative method in practical application, the method has also been used to reduce the noise of an experimental Lamb wave signal [19] and compared with the results of the EMD method and the WT method. The experimental data are analyzed using the Matlab platform. The experimental noisy S0 mode Lamb wave signal at a propagating distance of 120 mm in a 500 mm-by-300 mm stainless steel plate is shown in Fig. 6(a). The excitation signal is at a 420 kHz central frequency with 8 cycles. The received Lamb signal becomes spreading in the time domain resulted from the dispersion effect. The processed signals with different methods are shown in Figs. 6(b) to 6(d). When we use the WT method, as shown in Fig. 6(b), the noise can be eliminated effectively, but the part of main pulse signal is lost. When we use the EMD method, as shown in Fig. 6(c), the noisy signal cannot be eliminated effectively because the noise frequency is often quite low and exists in each component after the empirical mode decomposition. As shown in Fig. 6(d), when we use the fractional derivative method, the restoration of the main pulse signal is better than that of the other methods and is free from the burr.

5. Conclusion

In the present study, a noise reduction and SNR improvement method based on the fractional derivative is proposed for ultrasonic Lamb wave signals. After the fractional of the amplitude, the relationship between the peak amplitude and the derivative order as well as that between the peak frequency and the derivative order is created to extract the characteristic parameters of the amplitude spectrum. In comparison with the EMD and the WT methods, the proposed method can reduce the MSE and improve the SNR of the processed signal, even when the SNR is low. In short, this method can effectively reduce the noise for Lamb wave signals.