Noise removing for Lamb wave signals by fractional differential

1. Introduction

Ultrasonic Lamb wave is a common form of guided waves in the ultrasonic nondestructive testing and evaluation. It has become an important tool for the nondestructive evaluation [1-3], especially the large plate-like structures [4-6]. Compared with the other conventional ultrasonic testing methods, Lamb wave method has some advantages, such as long distance spreading along the structure and large detection area. Therefore, ultrasonic Lamb wave testing can be used in the complicated environment conveniently.

The received Lamb wave signal component is very complex in the actual detection due to the signal affected by different levels of noises, which impact the reliability and accuracy of detecting directly. There is thus a clear call for effective methods of noise removing for ultrasonic Lamb wave signals.

Many studies have been carried out for the noise removing of ultrasonic Lamb wave signals, such as the empirical mode decomposition (EMD) method and the wavelet transform (WT) method [7-13]. Li et al. tried an empirical mode decomposition method without predicting the overall characteristic and local characteristic of the original signal. But the noise reduction performance is not ideal, resulting in leaving many features of noise signals [7]. A de-noising algorithm of redundant second-generation wavelet transform considering neighboring coefficients was selected as the best solution in order to overcome the drawbacks of conventional wavelet de-noising methods that lost information in transforms. It can also improve the performance indexes, such as signal-to-noise ratio (SNR), mean square error (MSE), and correlation coefficient [8]. Matz et al. presented a comparative study of the discrete wavelet transform, the discrete stationary wavelet transform and the wavelet packets de-noising methods based on the wavelet transform. The best-performing method was wavelet packet de-noising, with SNRE within 15-40 dB [9]. Both wavelet threshold de-noising and empirical mode decomposition de-noising have their respective advantages and disadvantages, the former is effective for high signal-to-noise ratio, while the latter is still noisy after noise elimination. A noise reduction method for Lamb wave signals based on the empirical mode decomposition and the adaptive threshold wavelet transform was proposed [10]. To reduce the noise in the inspection data of an electromagnetic acoustic transducer, Huang et al. put forward a de-noising method using an envelope regulation technique. The algorithm can suppress small amplitude and high frequency noise mixed in the signal, without damaging the main feature of the signal. And it can also effectively eliminate the clutter and burrs in the inspection data, and improve the signal-to-noise ratio [11]. However, an effective method suitable for Lamb wave signals has not been proposed yet.

In order to further study the noise removing method in enhancing the resolution and the SNR of the Lamb wave signal, this paper proposes a noise removing method for Lamb wave signals based on the fractional differential (FD) theory. Both simulated and experimental data are used to evaluate the performance of the developed method qualitatively. The performance of this method is also compared with the empirical mode decomposition method and the wavelet transform method.

2. Developed fractional differential method

The developed method mainly consists of three steps. Firstly, the fractional differential of the amplitude spectrum of the received noisy signal at different orders is obtained with the fractional differentiation. Then, the characteristic parameters of the amplitude spectrum are extracted with the developed parameter estimation model. The Gaussian peak is used as a model to assign the amplitude spectrum of the original signal correctly. Finally, the waveform of the Lamb wave is restored by combining the amplitude and phase spectrums.

2.2. Parameter estimation

The fractional differential functions of $F\left(\omega \right)$ at different orders are shown in Fig. 1. It is shown that the zero-crossing point $F_0$ and the peak extremum $F_{max}$ of the fractional differential functions change as its corresponding differential order change. The relationship between the zero-crossing and peak extremum and the differential order are cube polynomial. Their functions are:

5

$F_{max}\left(v\right)=d_3{v}^3+d_2{v}^2+d_{1}v+d_0,$
$F_0\left(v\right)=c_3{v}^3+c_2{v}^2+c_{1}v+c_0,$

where $c_0$, $c_1$, $c_2$, $c_3$ are the coefficients of the cubic polynomial between the peak extremum and its corresponding differential order, and $d_0$, $d_1$, $d_2$, $d_3$ are the coefficients of the cubic polynomial between the zero-crossing point and its corresponding differential order.

Fig. 1The fractional differential functions at different orders

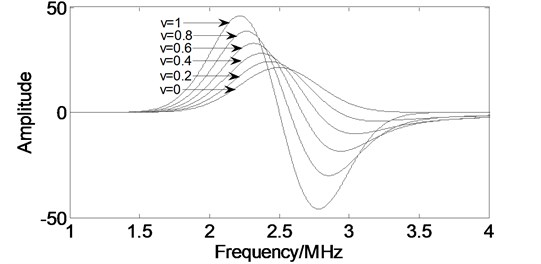
The zero-crossing point and the peak extremum are calculated by means of the numerical method. Two parameter estimation equations are modeled according to the relationship, and then we can obtain the parameter values of $\sigma$, $\mu$, and $A$. Due to the signal-to-noise ratio reduces with the increase of the differential order, we adopted low order differential to build parameter estimators. The expressions of the parameters can be written as:

6

$\left\{\begin{array}{l}\mu =c_3+c_2+c_1+c_0,\\ \sigma =\frac{d_0\sqrt{e}}{d_3+d_2+d_1+d_0},\\ A=d_0.\end{array}\right.$

The ultrasonic Lamb wave with the noise is analyzed based on the Fourier transform to obtain the amplitude and phase spectrums. Then the fractional differential of amplitude spectrum at different orders is gained with fractional differential. By the numerical method, we can get the value of the zero-crossing point and the peak extremum. The coefficients $c_0$, $c_1$, $c_2$, $c_3$, $d_0$, $d_1$, $d_2$, $d_3$ are fitted by the least square with the Eq. (5). The parameter values of $\sigma$, $\mu$, and $A$ can be gained by using the Eq. (6). Finally, the amplitude spectrum combines with the phase spectrum of the original signal to reconstruct the ultrasonic Lamb wave.

3. Simulation test

In this section, our purpose is to verify the noise removing performance of the developed FD method by using the simulated Lamb wave signal. A simulation is conducted [15] and compared with the empirical mode decomposition (EMD) method and the wavelet transform (WT) method. The simulated function mode of the Lamb wave signal with 3MHz center frequency and 800 kHz bandwidth is shown in Fig. 2. A normal white noise has been added to it in the time domain which SNR is 10 as shown in Fig. 3.

Fig. 2The original Lamb wave signal

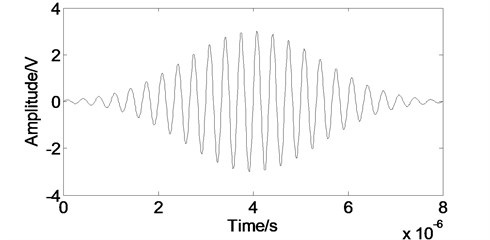
Fig. 3The Lamb wave signal with the noise

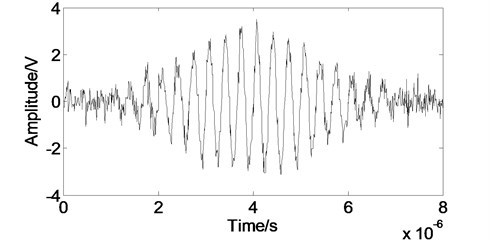
Fig. 4The Lamb wave signal after the EMD processing

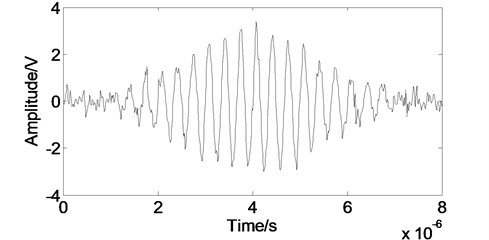
In the time domain, we compare the developed method with the others. As shown in Fig. 4, when we employ the EMD method, noise can not be eliminated effectively and the processed signal contains some noise burrs. As shown in Fig. 5, when we use the WT method, the noise removing effects is better than the EMD method, but some useful information are carried off. When we adopt the FD method, both the main pulse signal and the small signal are restored better than the others as shown in Fig. 6. Most of the white noise can be removed without burr. Above all, the developed method has the best noise removing performance for ultrasonic Lamb wave.

Fig. 5The Lamb wave signal after the WT processing

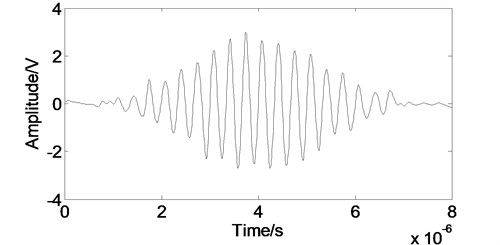
Fig. 6The Lamb wave signal after the developed processing

Different noise removing methods have their own advantages and limitations. In order to evaluate the noise removing performance quantitatively, which is based on three performance parameters, i.e. signal to noise ratio (SNR), the mean square error (MSE), and the smoothness index $r$.

Comparison of evaluation parameters with the above three methods when the SNR is 10 dB is shown in Table 1, meanwhile when the SNR is 5 dB is shown in Table 2. As summarized in the tables, after comparing with the EMD method and the WT method, the FD method can reduce MSE, $r$ and improve the SNR of the processed signal. Relative to those of the EMD method, the SNR is improved by about 11 dB and the MSE is reduced by about 13 dB. Relative to those of the WT method, the SNR is improved by about 9 dB and the MSE is reduced by about 11 dB. In a word, the FD method has the best noise removing performance for ultrasonic Lamb wave signals in the three methods.

4. Experiment

To evaluate the performance of the FD method in the practical application, a Lamb wave measurement system is set up to get the experimental Lamb wave signal. It is composed of the exciting probe, receiving probe, digital ultrasonic detector CTS-3000, RS232 interface, and the host computer [16]. The experimental process is controlled by the host computer.

In the experiment, the CTS-3000 detector is used to generate the excitation pulse and receive the ultrasonic Lamb signal. The detection sensitivity of CTS-3000 detector is up to 54 dB. The experimental workpiece is a stainless steel plate. The exciting and receiving probes are piezoelectric oblique longitudinal probes with wedges. They are coupled to the workpiece by the liquid film so that the ultrasonic wave can effectively be transmitted into the workpiece. The measurement data are sent to the host computer through the RS232 serial interface. The US3000 V1.0 software is used to record the data and save them into a text file for the later analysis. The experimental received noisy signal at a propagating distance of 3.5 cm is shown in Fig. 7.

Fig. 7The experimental Lamb wave signal

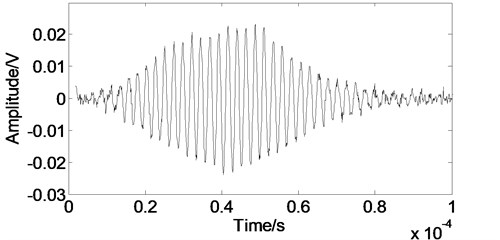
Fig. 8The Lamb wave signal after the WT processing

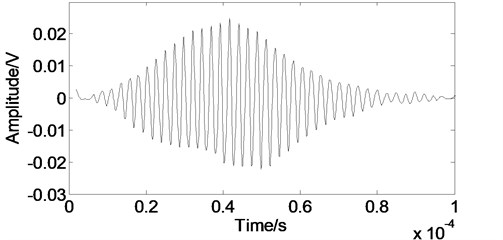
Fig. 9The Lamb wave signal after the EMD processing

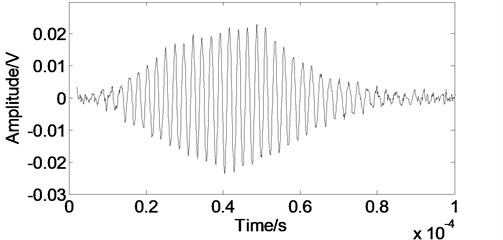
Fig. 10The Lamb wave signal after the developed processing

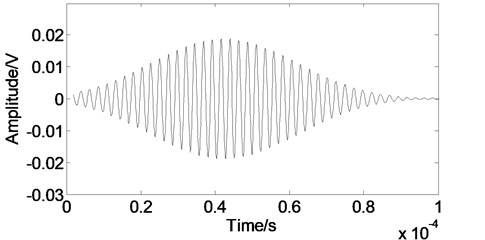
Fig. 11The spectrum of the experimental signal

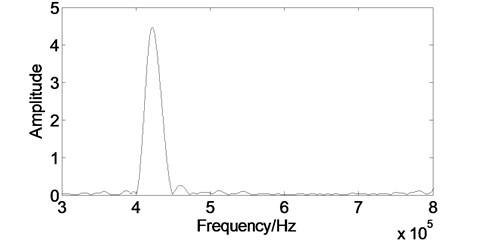
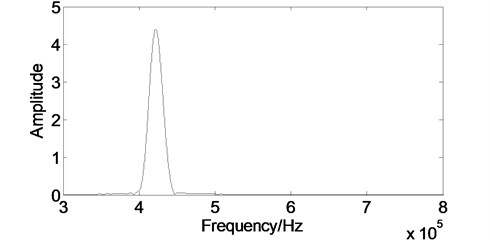
Fig. 12The spectrum after the WT processing

5. Results and discussion

To verify the performance of the developed method in practical applications, the developed method have also been applied to the experimental Lamb wave signal and compared with the EMD method and the WT method. The experimental data were analyzed on the Matlab platform. As shown in Fig. 8, when we employ the WT method, noise can be eliminated effectively, but part of the main pulse signal is lost. When we employ the EMD method as shown in Fig. 9, the received signal can not be eliminated effectively due to the noise frequency is often quite low and exists in each component after empirical mode decomposition. As shown in Fig. 10, when we use the developed method, the main pulse signal is restored better than the others and free from burr.

The effective of noise removing can not be accurately evaluated by those performance parameters quantitatively due to the experimental signal contains noise. So we considered the amplitude spectrum of the experimental signal as the comparison object. Fig. 11 is the amplitude spectrum of the original signal which reaches its maximum value at 0.42 MHz, and there are apparent noises in the amplitude spectrum. As shown in Fig. 12, when we employ the WT method, most of the white noise can be removed in the high frequency, but the method can not give a good performance near the main peak pulse. As shown in Fig. 13, when we adopt the EMD method, the amplitude spectrum is nearly as same as the original, thus the effect for removing the white noise is not obvious. As shown in Fig. 14, when we use the proposed method, the position of the main pulse peak values does not change, and the spectrum becomes smoother. Therefore, the developed method has better noise moving efficiency.

Fig. 13The spectrum after the EMD processing

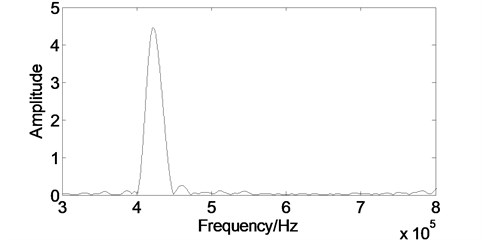
Fig. 14The spectrum after the developed processing

6. Conclusion

In this paper, a noise removing method based on the fractional differential is proposed for ultrasonic Lamb wave signals. Characteristic parameters of the amplitude spectrum can be calculated with parameters estimation model. By using the characteristic parameters we can restore the amplitude spectrum of the original signal correctly. The waveform of the ultrasonic lamb wave after noise removing is reconstructed by combining the amplitude spectrum with the phase spectrum. Compared with other methods, the developed method can reduce MSE, $r$ and improve the SNR of the processed signal. In short, the developed method has the best noise removing performance for ultrasonic Lamb wave signals.