Abstract
Modeling, identification and application of process damping in milling of titanium alloy is investigated. Titanium alloy used commonly in aviation industry is one typical difficult-to-machine material. Chatter usually occurs in cutting of titanium alloy, which results in poor surface quality and damaged tool. Thus, chatter is one important restriction for the quality and efficiency of titanium alloy manufacture. Process damping results from interference between flank face and machined surface, which is critical but usually ignored in chatter analysis for difficult-to-machine material. The paper presents one nonlinear dynamic model considering process damping for milling of titanium alloy and designs anti-vibration clearance angle to suppress chatter based on the model, besides, a practical approach based on Routh Criterion is proposed for the identification of process damping. The experimental and computational results indicate that the presented methods for modeling and identification of process damping are reasonable, and the anti-vibration clearance angle designed is effective in suppressing chatter and improving machining quality.
1. Introduction
Titanium alloy is used widely in aerospace industry, which possesses excellent overall performances owing to high specific strength, low density, strong heat and corrosion resistance. However, titanium alloy is also one typical type of difficult-to-cutting material, which possesses low machinability owing to poor thermal conductivity, high chemical activity and the severe hardening. Especially, due to large unit cutting force and low elastic modulus, chatter usually occurs in machining process. Vibration marks left on the machining surfaces is usually required to be removed manually, which result in low machining efficiency. Worse, it may result in scraped workpiece and destroyed tool. Chatter problem is one of the main restrictions to the machining quality and efficiency of titanium alloy.
The methods to suppress chatter can all be attributed to increase the damping of system. Damping of cutting system includes structural damping of machine tool and process damping (PD). Process damping results from interference between flank face of tool and undulations left on the workpiece. Tlusty and Ismail [1] showed that process damping has a significant effect on chatter stability decreasing with cutting speed. Structural damping can be identified using modal analysis easily. However, the identification and modeling of process damping has proved to be very difficult, and currently there is no practical method for its measurement or estimation. Altintas and Weck have addressed the process damping as the most challenging unsolved problems [2]. Therefore, in most of the studies, the effect of process damping is ignored, leading to significant errors in estimation of the stability limit [3-4].
In one of the early works, the regenerative chip thickness effect on process stability is modeled by Das and Tobias, where the contact between the tool flank face and the undulations left on the surface were not considered. In this work [5], a velocity term in addition to the structural damping is introduced into the system equations increasing process stability. Later on, the focus of the research on dynamic cutting force coefficients shifted toward the identification and modeling of dynamic cutting force coefficients. The results of the CIRP efforts on dynamic cutting are summarized by Tlusty [6], where the difficulty of the measurements and the inconsistency of the test data from different labs are discussed. Sission and Kegg [7], Wu [8], Lee et al. [9], and Elbestawi [10] showed that the contact forces due to flank-wave interaction contribute to the dynamic of the cutting process by increasing the overall damping acting on the system. Altintas et al. [11] developed a dynamic force model which includes chip thickness, velocity and acceleration terms. They identified dynamic cutting force coefficients from a series of dynamic cutting tests, where the cutting tool is oscillated by a fast tool servo at the desired frequency and amplitude.
Compared to turning, the reports on the process damping in milling are much fewer, because milling is one discontinuity and time-invariant cutting process and the descriptions of process damping are much more complicated. Huang C. Y. and Wang J. J. Junz [12-13] extended analytical modeling of the milling process to include process damping effects, two cutting mechanisms (shearing and plowing) and two process damping effects (direction and magnitude) are included. The analytical nature of this model makes it possible to determine unknown process damping coefficients from measured vibration signal during milling. Budak and Tunc [14-17] considered the effect of process damping as an additional damper in the zero order MFS. They identified the additional damping coefficients by measuring stability limits experimentally and fitting the results to the stability model, and investigated the effects of tool geometry and cutting conditions on process damping. Ahmadi and Ismail [18-19] simplified rocess damping to a piecewise linear viscous damper by assuming small amplitude of vibration, and integrated the equivalent viscous model of process damping into the Multi-Frequency Solution and the Semi-Discrete Method to establish the stability lobes in milling.
It can be known from above that higher stable cutting depth can be achieved under the effect of process damping, and high efficiency cutting can be achieved at low speeds. This can be important to increase machining productivity of titanium alloy, because low cutting speeds have to be used for longer tool life due to low machinability. Besides, process damping has a lot to do with tool geometry, design of tool geometry is very improtant in suppressing chatter. However, very few cases have been reported for the application of process damping in designing of tool for milling of titanium alloy.
In this paper, one nonlinear milling dynamic model considering process damping is presented. In the model, indentation area arises from face-wave interference is calculated and stability limit is predicted by time domain simulations. Based on the model, anti-vibration clearance angle is designed to increase process damping and expand stable region further. At last, one new method for analytical identification of process damping is presented, the process damping coefficients are identified directly and simply.
2. Modeling of process damping
2.1. Formation mechanism of process damping
The 2 DOF model shown in Fig. 1(a), is always used to describe the dynamics of the milling system [3, 4]. is the angular position of the th cutting tool, is the spindle speed. The vibration displacements of tool center determined in the workpiece coordinates (i.e., ) can be recorded as , the wave caused by vibration leave on the workpiece surface in direction (i.e., chip thickness or radial direction), direction represent the cutting speed direction. The interference between flank face and wave will occur when the chatter amplitude grows larger. Flank face intend into the wave left behind in radial direction as shown in Fig. 1. As a result, indentation forces (i.e., and ), arise in normal, , and frictional, , directions on the tool flank face as shown in Fig. 1(b), which create a damping effects. The damping forces in and directions acting on each tooth are oriented and summed up as a resultant damping force in and directions.
Fig. 1End milling system dynamics
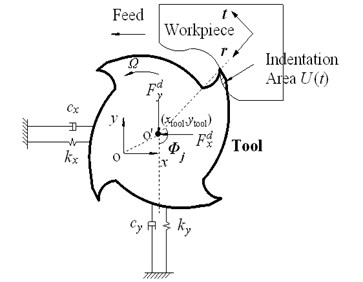
a)
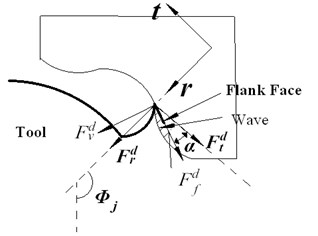
b)
Fig. 2Formation mechanism of indentation area
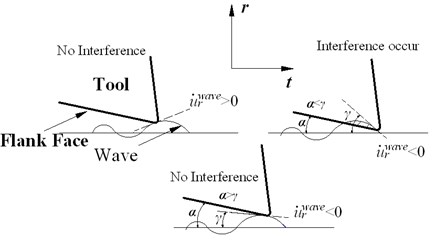
a)
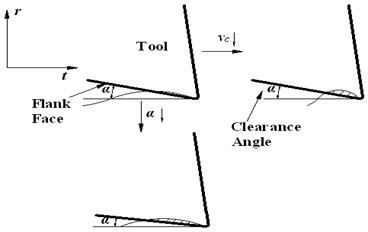
b)
Process damping is proportional to indentation area. In Fig. 2(a), is the clearance angle of tool, angle represent the slope of wave left in radial direction, is the radial coordinate values of wave, which represent the radial vibration displacement. The instantaneous slope of wave, represent the radial vibration speed (i.e., ). It is assumed that the tool does not indent the previous wave as shown in Fig. 2(a). Therefore, the interference between flank face and workpiece occurs only as the tool slide down the wave, where . The occurrence of interference is determined by the relationship between and . If satisfies the conditions:
The interference will occur. In Eq. (1), is the cutting speed, represents tangential arc length of tool edge, is time here. It can be known from Eq. (1) that interference is easy to occur as and decreases, indentation area and process damping will also increase. The law is also shown in Fig. 2(b).
2.2. Calculation of indentation area
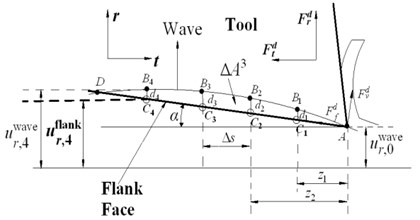
The calculation of indentation area shown in Fig. 1(a) is rather complicated. As shown in Fig. 3, the cutting tool is divided into a number of axial elements, elemental axial width is . In axial level , point represents the current position of the tool edge, which can be also seen in Fig. 4(a), correspondingly, is the current radial coordinate values of wave. As shown in Fig. 4(a), (1, 2, 3...) represent the point on the surface wave generated by the tool edge in the previous time step, corresponding radial coordinate values of wave calculated in previous time steps is . For every , is the corresponding point on the flank face, is its radial coordinate values. The distance between and is . is zero. The indentation area in every axial level is bounded by the tool flank face and the workpiece surface wave. This area is calculated at each simulation time step numerically.
Fig. 3Digitized end mill model
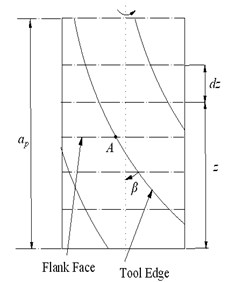
Fig. 4Calculation of indentation area
a)
b)
The calculation of is calculated according to Eq. (2), here, is the tangential arc length between adjacent two time point. is the simulation time step:
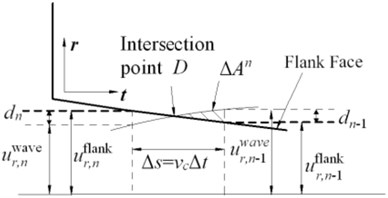
The intersection point of flank face and wave, , needs to be searched in the calculation process. As shown in Fig. 4(b), when , the calculation of indentation area can stop. The number of time step front and back intersection can be recorded as and respectively, here , , thus, indentation area can be calculated by summing up the discrete areas according to Eq. (3):
2.3. Effects of anti-vibration clearance angle on process damping
It can be seen from Eq. (1) that interference is much easier to occur and process damping is more significant as cutting speed decreases, smaller clearance angle can lead to the same effects. However, in the tool design, severe extrusion is easy to occur and the surface quality will become very poor if the clearance angle is too small. Therefore, transition edge needs to be adopted in design. As shown in Fig. 5, the tool modified have two clearance angle, and , is designed to be smaller to suppress vibration, which can be named anti-vibration angle, the length of its corresponding transition edge is .
Fig. 5Effects of anti-vibration clearance angle on indentation area
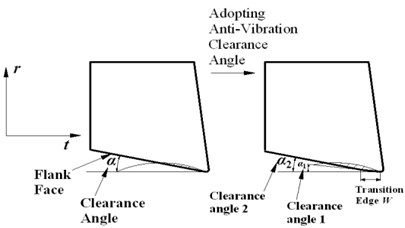
Fig. 6Calculation of indentation area with anti-vibration clearance angle
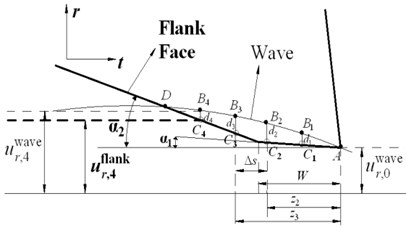
The calculation of indentation area follows the methods provided in Section 2.2, the main parameters in Fig. 6 is the same as ones in Fig. 4(a). Minor modification needs to be done because the adoption of anti-vibration clearance angle. The calculation of follows Eq. (4), then the calculation of indentation area also follow the Eq. (3):
3. Time domain simulations
3.1. Equations of milling dynamics
Dynamic cutting force model is of great importance in analysis of milling dynamics. At each axial level , the location of theth cutting tooth is determined by its angular position (as shown in Fig. 1):
In Eq. (5), is the number of teeth, is the helix angle (as shown in Fig. 3), is the tool radius. is the angular position of tool bottom (axial level ), calculated from angular velocity and the time : .
The dynamic cutting force is modeled using the linear-edge force model [20], where elemental tangential and radial forces, and , at flute, , are expressed in terms of cutting pressure coefficients, , cutting edge force coefficients, , instantaneous chip thickness, , and elemental axial width, (as shown in Fig. 3):
The differential cutting forces are then oriented in and directions using the forces in and directions as follows:
For the th cutting flute, differential indentation forces acting on the axial level, in normal, and in frictional directions are given as:
where is the indentation area at axial level , which is calculated by methods provided in Section 2.2-2.3. is the coefficient of contact friction between the flank face and the workpiece surface, is indentation coefficient. The process damping force in and directions are expressed in terms of the forces in direction and the friction coefficient (as shown in Fig. 1(b)):
The differential process damping forces are then oriented in and directions using the process damping forces in and directions as follows:
Thus, equations of milling dynamic can be modeled:
where, is the numbers of axial elements (, is axial cutting depth), milling at small radial immersion is adopted in the paper, generally, only one tooth is cutting workpiece in one tooth passing period. (), (), () are the modal mass, modal damping, modal stiffness respectively (as shown in Fig. 1(a)), which can be obtained from modal tests and analysis. () is the vibration displacement of tool, which is also shown in Fig. 1(a). is a unit step function which determines whether the tooth is in or out of the cutting, which will be discussed in Appendix. Besides, the calculation of dynamic chip thickness in Eq. (6) and in Eq. (2) are rather complicated, which will be also discussed in detail in Appendix.
3.2. Determining chatter stability lobes from time domain simulations
The Eq. (11) is solved using the classical 4th order Runge Kutta method, where time increment is adopted as 10-5 seconds. Using the following steps, the stability lobes are evaluated by finding the limiting axial cutting depth through a range of spindle speeds:
1. Modal parameters of machine tool structure, cutting tool geometry, feed rate, tool orientation, entry angle and exit angle, cutting force coefficients, and a starting axial cutting depth, , are specified.
2. A range of spindle speeds and a spindle speed step size are specified.
3. For a given spindle speed, a static time domain simulation is run (suppressing any tool and workpiece vibrations) and the maximum static uncut chip thickness, , is stored.
4. A second time domain simulation is run. For given spindle speed and cutting depth, Eq. (11) is solved, vibration displacements and dynamic chip thickness is obtained. The largest dynamic chip thickness of all cutting points on the tool, is stored for the last few revolutions of the simulation.
5. The non-dimensional chatter parameter, , is evaluated as:
6. If is greater than a pre-determined limit (1.25 is used in this thesis), the process is unstable, otherwise the process is stable. The criterion to judge is provided in [21].
7. If the process is stable, is set to the current value of , is doubled and steps 3-6 are repeated until chatter occurs. Then is set to the value of when chatter occurred.
If the process is unstable, is set to the current value of , is halved and steps 3-6 are repeated until the process is stable. Then is set to the stable axial cutting depth, .
8. Once the range to is found between which the limiting axial cutting depth lies, a bisection search is performed with , repeating steps 3-6 until the limiting axial cutting depth, , is found within a given tolerance.
4. Identification of process damping
Before the identification of process damping, one new approach to predict stability limits needs to be introduced.
4.1. Analysis of milling dynamic equations based on Routh criterion
If nonlinear effects such as process damping are ignored, linear time-delay model such as zero order solutions are always adopted in generating stability lobes [4], which can predict stability limit accurately at higher speed. According to classical zero order solutions [3], the equations of milling dynamics are shown in Eq. (13). , , , shown in Eq. (13) stand for the average directional coefficients, which relate the dynamic displacements to the dynamic cutting forces. is the axial cutting depth. The physical meanings of other parameters in Eq. (13) are the same as ones in Eq. (11), , :
The paper presents one new method to analyze the root reason of the occurrence of chatter.
Firstly, the Eq. (13) is converted from time to frequency domain:
Eq. (14) can be written simply:
where, is the dynamic stiffness matrix of milling system. The characteristic equations of milling system can be obtained from Eq. (15):
The expansion of Eq. (16) is shown as follows:
Additional damping elements:
Additional stiffness elements:
In Eq. (13), in general [3]. For regenerative chatter, the phase [3], thus . For additional damping terms, , , for additional stiffness terms, , . It is the non-diagonal elements that cause chatter, which can be verified by Routh criterion [22]. In Eq. (17), can be replaced by , and the equation can be transformed into Laplace domain:
Eq. (20) can be expanded:
where:
The first row of Routh criterion table is:
According to Routh criterion [22], the system becomes unstable when there are negative elements in Eq. (23). In Eqs. (18)-(19), thus then , then , as a result, decrease. The coefficient decreases obviously as a result of decreasing. Meanwhile, the other elements in Eq. (23) have no obvious trends to decrease. Thus, the limiting axial cutting depth can be predicted when the become negative as increases. The prediction method will be verified by milling experiments.
4.2. Identification of process damping
From Section 4.1, it could be concluded that the way to suppress chatter can be attributed to increase diagonal elements, () or eliminate non-diagonal elements , (), these ways can all increase the in Eq. (23) to increase stability. In [14-17], the effects of process damping is considered as an additional damper , . Obviously, the process damping can improve limiting axial cutting depth by increasing ().
Fig. 7Variations in absolute stability limits with cutting speed
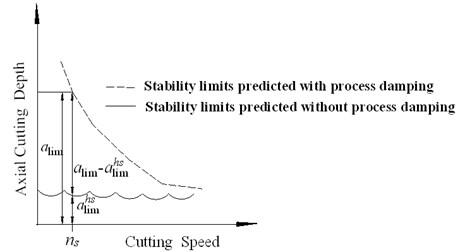
In general, according to linear time-delay model ignoring process damping, there is hardly any stability lobes and stability limits are very small at low speed as shown in Fig. 7, which is due to the many tightly packed vibration waves at each tooth period [3]. As discussed in Section 2, the indentation area and process damping increase as the cutting speed decreases, therefore the absolute stability limit commonly varies with cutting speed as shown in Fig. 7. The stability limit decreases at higher speeds, where the effect diminishes. For given speed , is the stability limits predicted ignoring process damping, which can be generated by time simulation methods provided in Section 3, where process damping force is ignored in Eq. (11). Whereas is generated when process damping force is considered in Eq. (11). The process damping is identified using the differences between and .
Considering the symmetry of tool structures, the modal parameters (, , , , ) in two different directions can be assumed as equal: , , . Structural damping ratio . Thus, for given spindle speed, the process damping can be identified following the steps as below:
1) Generate and .
2) Entitle value: .
3) Increase damping ratio: ( is taken as 0.0001).
4) For given , obtain new critical cutting depth . In the step, axial cutting depth , increases from until is negative, then .
5) If , go to step 3, otherwise, . Where, is total damping ratio, which is the sum of structural damping ratio and process damping ratio.
Then, the process damping can be obtained as follows:
5. Comparison of computational and experimental results
To verify the nonlinear model and identification method provided in Sec.1-4, the computations and experiments are all achieved. Computations are achieved in MATLAB according to time domain simulation provided in Section 3, the modal parameters in Eq. (11) are:
Natural frequency: 2061 Hz.
Modal damping ratio: 0.026.
Modal stiffness: 1.044×107 N/m.
Cutting force coefficients: tangential force coefficient 2000 MPa, 41 N/mm, radial force coefficients 1000 MPa, 77 N/mm, which are obtained by slot milling identification [3].
Process damping coefficients: indentation coefficient and friction coefficient , for titanium alloy Ti6AL4V were reported at 30,000 N/mm3 and 0.3 in [15]. To show the effects of process damping, the stability limits predicted without process damping are also generated.
Fig. 8The milling experiments scenes

Test scenes are shown in Fig. 8, experimental equipments:
Machine: Mikron UCP DURO800.
Tool 1: carbide end mill, 125 mm overall length, 70 mm overhang length, 30 mm edge length, 12 mm diameter, 4 flutes, 30° helix angle, 9° clearance angle.
Tool 2 (with anti-vibration clearance angle): clearance angle – is 4°, is 9°, length of transition edge – 60 μm, the other parameters are the same as tool 1.
Sensors: piezoelectric acceleration sensors to collect vibration signals of workpiece; AE sensors to collect sound signals.
Workpiece material: Ti6AL4V.
Data acquisition card: NIUSB9233.
Main parameters: radial cutting depth 1 mm, feed per tooth 0.06 mm/z, down milling, mist cooling.
Fig. 9Stability limits generated from computations and experiment
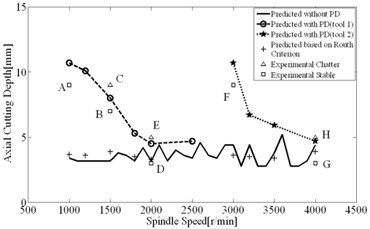
Fig. 10Process damping identified based on Routh criterion
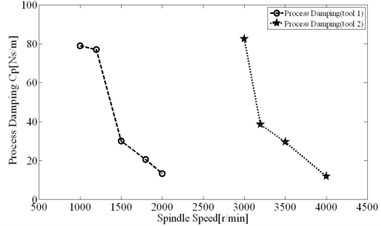
Fig. 11Spectral analysis results (tool 1)
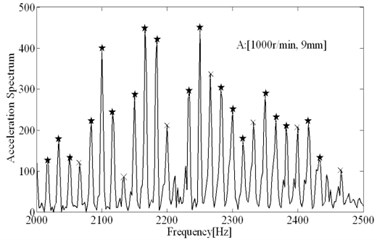
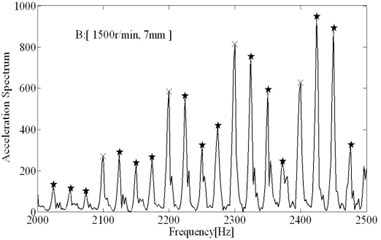
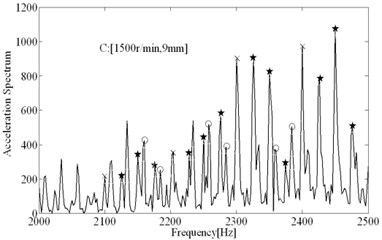
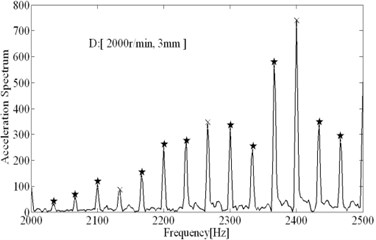
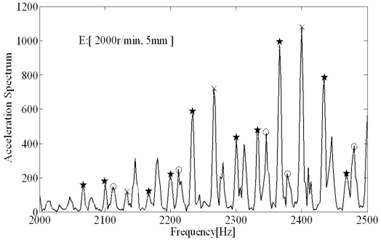
The comparisons of computational and experimental results are shown in Fig. 9, the spectral analysis results of vibration signals measured are shown in Figs. 11-12. From the spectral analysis of vibration and sound signals measured, it is observed that the frequency with high peak value concentrates on the region from 2000 Hz to 2500 Hz. Besides, chatter frequency is close to structural natural frequency [3]. Therefore, to see the spectrum clearly (spectral lines are very dense due to low rotating speed), the analytical region from 2000 Hz to 2500 Hz is shown in Figs. 11-12. It can be seen that the main frequency are all spindle rotating frequency (recorded as star) and tooth passing frequency (recorded as “×”) in stable conditions, while the chatter frequency (recorded as “○”) become prominent in unstable conditions. In unstable conditions (chatter), the phase and chatter frequency don’t coincide with spindle rotating frequency, the unstable types belong to Hopf bifurcation. From Fig. 9, it is seen that the estimations on the stable limits show a good agreement with the experimental results. Besides, the stability limits identified based on Routh criterions are shown in Fig. 9, which show a good agreements with stability limits predicted by time domain simulations. It indicates that the method for identification of process damping is reasonable. The process damping identified are shown in Fig. 10, For tool 1, the effect of process damping lasts until the spindle speed is up to 2000 r/min (cutting speed m/min). For tool 2, stable regions are expanded remarkably relative to tool 1. The effects of process damping increase due to anti-vibration clearance angle, which lasts until the spindle speed exceeds 3000 r/min (cutting speed 113 m/min).
Fig. 12Spectral analysis results (tool 2)
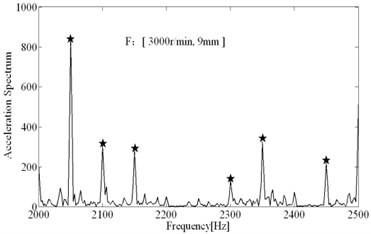
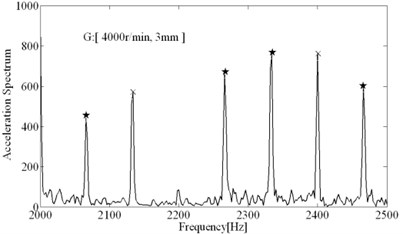
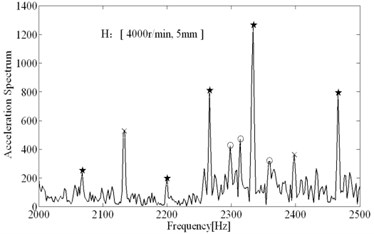
Fig. 13The comparisons of spectral analysis results
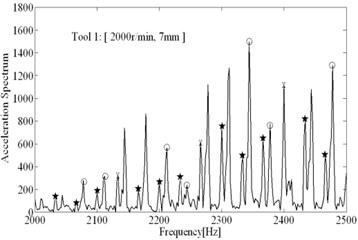
a) Tool 1
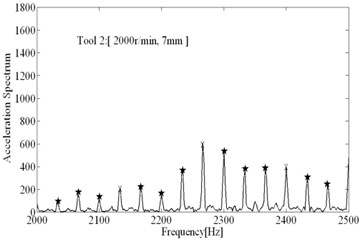
b) Tool 2
To show the performances of anti-vibration clearance angle in suppressing chatter well, the unstable condition (2000 r/min, 7 mm) when using tool 1 can be achieved with tool 2 again. As shown in Fig. 13, a) shows the spectral analysis results when using tool 1, chatter frequency is prominent; b) shows the spectral analysis results when using tool 2, the chatter frequency have been almost eliminated and main frequency all represents imposed vibration, besides the peak value are much lower than using tool 1, the effects of tool 2 in suppressing chatter are significant. In Fig. 14(a), lots of inclined vibration marks are left on the machined surface when using tool 1, which is the symbol of the occurrence of regenerative chatter. Whereas in Fig. 14(b), the surface is very smooth and only little straight marks are left (it indicates the slight imposed vibrations) when using tool 2, anti-vibration clearance angle have significant effects.
Fig. 14The comparisons of surface quality

a) Tool 1

b) Tool 2
For the same cutting parameters (2000 r/min, 7 mm), the dynamic chip thickness, , calculated under three different conditions are shown in Fig. 15, which can indicate the criterion to judge is provided in Section 3 is valid.
Fig. 15The dynamic chip thickness in different conditions
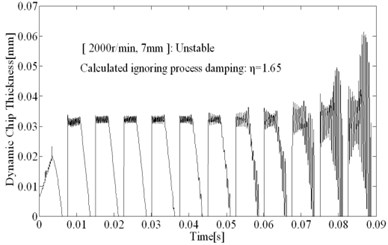
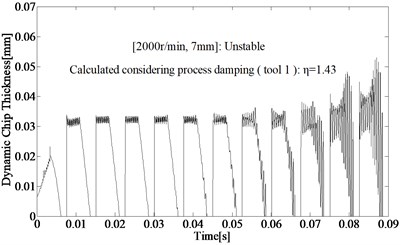
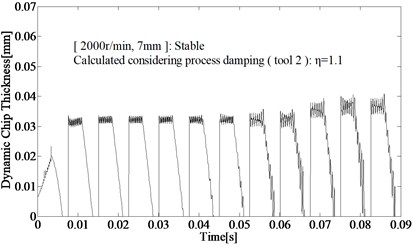
The comparative analysis of computational and experimental results show that the non- linear model considering process damping can predict stability limits at low speed in the milling of typical titanium alloy accurately, including the working conditions using tool with anti-vibration clearance angle. For tool 1, process damping can expand the stable regions significantly, limits can be improved from 3 mm to 10 mm at regular spindle speed such as 1000 r/min (cutting speed 40 m/min) in milling of titanium alloy. The tool 2 can increase the process damping further and expand the speed range of process damping effect, the laws presented by Eq. (1) are proved fully.
6. Discussions and conclusions
Chatter problem in milling of titanium alloy is one of the main restrictions to the quality and efficiency of aeronautical manufacture. In the machining of titanium alloy, quite low cutting speed is always adopted for ensuring the tool life. Stability limits predicted by regular model ignoring process damping is much lower than actual limits, which may lead to terrible machining efficiency. In the paper, one milling dynamic model considering process damping is presented to predict stability limit and one simple method based on Routh criterion is presented for identification of process damping. The computations and experiments indicates that the nonlinear model could provide accurate results and the identification method is reasonable. Besides the anti-vibration clearance angle designed could increase process damping to suppress chatter and improve machining surface quality effectively. Furthermore, the anti-vibration angle can expand speed range of process damping effects significantly, the conclusion has not been proposed in previous works.
However, it must be pointed out that the calculation model of process damping proposed in paper is a simplification of a much complicated interaction between the cutting edge, the flank face, and the workpiece. The interaction is highly dependent on the edge condition, and in particular on tool wear. In the current work, only sharp cutters were utilized.
In summary, although lots of simplifications have been adopted in computational model, the importance and effect of model can be also shown in paper. In future work, more complex tool geometry will be tried out, the effect of honed radius and flank wear will be investigated.
References
-
Tlusty J., Ismail F. Special aspects of chatter in milling. Journal of Engineering for Industry, Vol. 105, Issue 1, 1983, p. 24-32.
-
Altintas Y., Weck M. Chatter stability in metal cutting and grinding. CIRP Annals – Manufacturing Technology, Vol. 53, Issue 2, 2004, p. 619-642.
-
Altintas Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. Second Edition, Cambridge University Press, London, 2011.
-
Altintas Y., Stepan G., et al. Chatter stability of milling in frequency and discrete time domain. Journal of Manufacturing Science and Technology, Vol. 1, Issue 1, 2008, p. 35-44.
-
Das M. K., Tobias S. A. The relation between the static and the dynamic cutting of metals. International Journal of Machine Tool Design and Research, Vol. 7, Issue 2, 1967, p. 63-89.
-
Tlusty J. Analysis of the state of research in cutting dynamics. Annals of the CIRP, Vol. 27, Issue 2, p. 583-589.
-
Sisson T. R., Kegg R. L. An explanation of low-speed chatter effects. Journal of Engineering for Industry, Vol. 91, Issue 4, 1969, p. 951-958.
-
Wu D. W. A new approach of formulating the transfer function for dynamic cutting process. Journal of Engineering for Industry, Vol. 111, Issue 1, 1989, p. 37-47.
-
Lee B. Y., Tarng Y. S., Ma S. C. Modeling of the process damping force in chatter vibration. International Journal of Machine Tools and Manufacture, Vol. 35, Issue 7, 1995, p. 951-962.
-
Shawky A. M., Elbestawi M. A. An enhanced dynamic model in turning including the effect of ploughing forces. Journal of Manufacturing Science and Engineering, Vol. 119, Issue 1, 1997, p. 10-20.
-
Altintas Y., Eynian M., Onozuka H. Identification of dynamic cutting force coefficients and chatter stability with process damping. Journal of Manufacturing Science and Engineering, Vol. 57, Issue 1, 2008, p. 371-374.
-
Huang C. Y., Wang J. J. Junz Mechanistic modeling of process damping in peripheral milling. Journal of Manufacturing Science and Engineering, Vol. 129, 2007, p. 12-20.
-
Huang C. Y., Wang J. J. Junz Effects of cutting conditions on dynamic cutting factors and process damping in milling. International Journal of Machine Tools & Manufacture, Vol. 51, Issue 4, 2011, p. 320-330.
-
Budak E., Tunc L. T. A new method for identification and modeling of process damping in machining. Journal of Manufacturing Science and Engineering, Vol. 131, Issue 5, 2009, p. 1-10.
-
Budak E., Tunc L. T. Identification and modeling of process damping in turning and milling using a new approach. CIRP Annals-Manufacturing Technology, Vol. 59, Issue 1, 2010, p. 403-408.
-
Tunc L. T., Budak E. Effect of cutting conditions and tool geometry on process damping in machining. International Journal of Machine Tools and Manufacture, Vol. 57, 2012, p. 10-19.
-
Tunc L. T., Budak E. Identification and modeling of process damping in milling. Journal of Manufacturing Science and Engineering, Vol. 135, Issue 2, 2013, p. 1-12.
-
Ahmadi K., Ismail F. Experimental investigation of process damping nonlinearity in machining chatter. International Journal of Machine Tools and Manufacture, Vol. 50, Issue 11, 2010, p. 1006-1014.
-
Ahmadi K., Ismail F. Stability lobes in milling including process damping and utilizing multi frequency and semi-discretization methods. International Journal of Machine Tools and Manufacture, Vol. 54-55, 2012, p. 46-54.
-
Budak E., Altintas Y., Armarego E. J. A. Prediction of milling force coefficients from orthogonal Transactions of ASME Journal of Engineering, Vol. 118, Issue 2, 1996, p. 216-224.
-
Campomanes Marc L., Altintas Y. An improved time domain simulation for dynamic milling at small radial immersions. Journal of Manufacturing Science and Engineering, Vol. 125, 2003, p. 416-422.
-
Gupta S. Elements of Control Systems. China Machine Press, Beijing, 2004.
About this article
The research is sponsored by the National Natural Science Funds (No. 51475234, 51375236).
