Periodic solution to a nonlinear oscillator arising in micro electro mechanical system

Nikkar, A.; Jodeiri, H.; Ahari Abesh Ahmad, Sh.; Tariverdian, H.

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2015

Check for updates

Periodic solution to a nonlinear oscillator arising in micro electro mechanical system

A. Nikkar¹

H. Jodeiri²

Sh. Ahari Abesh Ahmad³

H. Tariverdian⁴

¹Young Researchers and Elite Club, Ahar Branch, Islamic Azad University, Ahar, Iran

²Young Researchers and Elite Club, Tabriz Branch, Islamic Azad University, Tabriz, Iran

³Faculty of Civil Engineering, University of Tabriz, Tabriz, Iran

⁴Department of Civil Engineering, Sardroud Branch, Islamic Azad University, Sardroud, Iran

Corresponding Author:

H. Jodeiri

Cite the article Download PDF

Downloads 1089

Abstract

In this paper, a periodic solution of nonlinear oscillator arising in the micro-beam based microelectromechanical system (MEMS) has been analytically achieved. The Amplitude Frequency Formulation (AFF) and Max Min Approach (MMA) have been used. In the second method (which is called MMA), an approximate solution of the nonlinear equation can be easily deduced by finding Maximal and minimal solution thresholds of this nonlinear problem. What we understood is that both methods, works properly and scales down the deal of the work. Compare conclusions with the results from fourth order Runge-Kutta method and energy balance method (EBM) shows that obtained results are of high accuracy and convenient.

1. Introduction

Study micro-electro-mechanical systems (MEMS) are batch-fabricated devices and structures at a microscale level [1] which can be defined as a system of small dimensions (less than one cubic centimeter) fulfilling a smart function. Since its inception, MEMS technologies are of tremendous importance in various engineering fields. Because of its small size, low power consumption and high reliability, we have seen many potential applications of MEMS devices which require few mechanical components and small voltage levels for actuation actuators and sensors in aerospace, optical and biomedical engineering [2-4]. MEMS devices are generally classified according to their actuation mechanisms. Actuation mechanisms for MEMS vary depending on the suitability to the application at hand. The most common actuation mechanisms are electrostatic, pneumatic, thermal, and piezoelectric [5]. With reported successes in applications ranging from signal filtering to chemical and mass sensing, electrostatically actuated resonant microbeam devices which form a broad class of MEMS devices due to their simplicity, as they require few mechanical components and small voltage levels for actuation [5] continue to be one of the most widely studied topics of the MEMS community.

Almost every natural event can be modeled with nonlinear equations; this is due to nature of the phenomena in the world. Although it is easy to find the solutions of some problems by using of computers, it is still difficult to solve nonlinear equations either numerically or analytically. Also it is very difficult to obtain the exact answer for these equations. Nonlinearity in MEMS which may cause some difficulties in computations, is made by Electrostatic actuation, large deflections and damping. According to these difficulties, some analytic techniques are available for nonlinear problems, such as MEMS [5-15]. Amplitude Frequency Formulation and Max Min approach (MMA), suggested by J. H. He. [16, 17]. Both methods are simple and effective methods to solve nonlinear oscillatory equations. In this paper, AFF and MMA are used to study a nonlinear oscillator arising in the micro-beam based MEMS where the mid plane stretching effect and distributed electrostatic force are both considered.

2. Problem description

Consider a clamped-clamped microbeam-based electromechanical resonator with uniform thickness $h$ , length $l$ , width $b$ ( $b \geq 5 h$ ), effective modulus $\bar{E} = E / (1 - ν)^{2}$ , Young’s modulus $E$ , Poisson’s ratio $v$ and density $q$ , as shown in Fig. 1 together with coordinate $o x y z$ , where $g_{0}$ is the initial gap and $V$ the electrostatic load. The equation of motion that governs the transverse deflection is written as:

1

\bar{E} I \frac{\partial^{4} w}{\partial x^{4}} + ρ S \frac{\partial^{2} w}{\partial t^{2}} - [\bar{N} + \frac{E S}{2 l} {\int_{0}^{l} (\frac{\partial w}{\partial x})}^{2}] \frac{\partial^{2} w}{\partial x^{2}} = q (x, t),

where $S = b h$ and $\bar{N}$ denotes the tensile or compressive axial load created by the mismatch of both thermal expansion coefficient and crystal lattice period between substrate and the thin film (microbeam). The second term on the right-hand side, $q (x, t)$ , denotes the driving force per unit length, resulting from electrostatic excitation [18]. Using the classical beam theory and taking into account of the mid-plane stretching effect as well as the distributed electrostatic force, the following dimensionless equation of motion for the microbeam can be formulated via the Galerkin method [18]:

2

\ddot{u} (a_{1} u^{4} + a_{2} u^{2} + a_{3}) + a_{4} u + a_{5} u^{3} + a_{6} u^{5} + a_{7} u^{7} = 0,

where:

3

a_{1} = \int_{0}^{1} ϕ^{6} d ζ,

4

a_{2} = - 2 \int_{0}^{1} ϕ^{4} d ζ,

5

a_{3} = \int_{0}^{1} ϕ^{2} d ζ,

6

a_{4} = \int_{0}^{1} (ϕ'''' ϕ - N ϕ'' ϕ - V^{2} ϕ) d ζ,

7

a_{5} = - \int_{0}^{1} (2 ϕ'''' ϕ^{3} - 2 N ϕ'' ϕ^{3} + α ϕ'' ϕ \int_{0}^{1} (ϕ')^{2} d ζ) d ζ,

8

a_{6} = \int_{0}^{1} (ϕ'''' ϕ^{5} - N ϕ'' ϕ^{5} + 2 α ϕ'' ϕ^{3} \int_{0}^{1} (ϕ')^{2} d ζ) d ζ,

9

a_{7} = - \int_{0}^{1} (α ϕ^{'' ϕ^{5} \int_{0}^{1} (ϕ')^{2}} d ζ) d ζ,

and

10

ϕ = 16 ξ^{2} (1 - ξ^{2}) .

Here, an overdot ( $∙$ ) represents differentiation with respect to the time variable, while a prime ( $'$ ) demonstrates the partial differentiation with respect to the coordinate variable $ξ$ .

3. Basic idea of amplitude frequency formulation (AFF)

To illustrate the basic idea of AFF method, the following nonlinear oscillator is considered:

11

\ddot{u} + N (\ddot{u}, \dot{u}, u, t) = 0, u (0) = A, \dot{u} (0) = 0 .

For a generalized nonlinear oscillator in Eq. (11), we use two trial functions:

12

u_{1} = A c o s ω_{1} t, ω_{1} = 1,

13

u_{2} = A c o s ω_{2} t, ω_{2} = ω,

where $ω$ is assumed to be the frequency of the nonlinear oscillator, Eq. (11). The residuals are:

14

R_{1} (t) = - c o s t + f (A c o s t),

15

R_{2} (t) = - ω^{2} c o s (ω t) + f (A c o s (ω t)) .

Fig. 1Schematics of a fixed microbeam-based electromechanical resonator [18]

We introduce $R_{11}$ and $R_{22}$ defined as:

16

R_{11} (t) = \frac{4}{T_{1}} \int_{0}^{\frac{T_{1}}{4}} R_{1} (t) \cos (t) d t, T_{1} = 2 π,

17

R_{22} (t) = \frac{4}{T_{2}} \int_{0}^{\frac{T_{2}}{4}} R_{2} (t) \cos (ω t) d t, T_{2} = \frac{2 π}{ω} .

Applying He’s frequency-amplitude formulation, we have:

18

ω^{2} = \frac{ω_{1}^{2} R_{22} (t) - ω_{2}^{2} R_{11} (t)}{R_{22} (t) - R_{11} (t)},

where $ω_{1} =$ 1 and $ω_{2} = ω$ .

4. Basic idea of max-min approach

In this section, MMA is applied to discuss the problem. To illustrate the basic idea of MMA method, the following nonlinear oscillator is considered:

19

\ddot{u} + N (\ddot{u}, \dot{u}, u, t) = 0, u (0) = A, \dot{u} (0) = 0 .

In order to the fact that small parameters or linear terms are not the requirements of MMA, Eq. (18) can be approximately solved by using the MMA. Considering $a$ , $b$ , $c$ and $d$ as the real numbers:

20

\frac{a}{b} < x < \frac{d}{c} .

Then:

21

\frac{a}{b} < \frac{m a + n d}{m b + n c} < \frac{d}{c},

where $m$ and $n$ are weighting factors and $x$ is a rough approximation of:

22

x = \frac{m a + n d}{m b + n c} .

Eq. (19) can be rewritten in the following form:

23

\ddot{u} + u f (\ddot{u}, \dot{u}, u, t) = 0 .

And the frequency can be identified as follows:

24

\frac{a}{b} < ϖ^{2} = \frac{m a + n d}{m b + n c} < \frac{d}{c} .

Then:

25

\ddot{u} + ϖ^{2} u = \ddot{u} + N (\ddot{u}, \dot{u}, u, t) + ρ (\ddot{u}, \dot{u}, u, t),

26

ρ (\ddot{u}, \dot{u}, u, t) = 0,

here $ϖ$ can be obtained by substitution of $A c o s (ϖ t)$ as initial assumption into Eq. (25).

5. Implementation of AFF

In this section, in order to assess the accuracy of He’s amplitude-frequency formulation for solving nonlinear governing equation of motion and to compare it with the other solutions, in this section we consider this method. According to He’s amplitude-frequency formulation, we choose two trial functions $u_{1} (t) = A c o s t$ and $u_{2} (t) = A c o s ω t$ , where $ω$ is assumed to be the frequency of the nonlinear oscillator Eq. (2). Substituting the trial functions into Eq. (10) results in, respectively, the following residuals:

27

R_{1} (t) = - (a_{1} A^{4} c o s (t)^{4} + a_{2} A^{2} c o s (t)^{2} + a_{3}) \times A c o s (t) + a_{4} A c o s (t) + a_{5} A^{3} c o s (t)^{3}

+ a_{6} A^{5} c o s (t)^{5} + a_{7} A^{7} c o s (t)^{7},

28

R_{2} (t) = - (a_{1} A^{4} c o s (ω t)^{4} + a_{2} A^{2} c o s (ω t)^{2} + a_{3}) \times A c o s (ω t)^{2} ω^{2} + a_{4} A c o s (ω t)

+ a_{5} A^{3} c o s (ω t)^{3} + a_{6} A^{5} c o s (ω t)^{5} + a_{7} A^{7} c o s (ω t)^{7} .

We introduce $R_{11}$ and $R_{22}$ defined as:

29

R_{11} (t) = \frac{4}{T_{1}} \int_{0}^{\frac{T_{1}}{4}} R_{1} (t) c o s (t) d t = \frac{1}{128} A \times (40 a_{6} A^{4} - 40 a_{1} A^{4} - 48 a_{2} A^{2} + 48 a_{5} A^{4}

+ 35 a_{7} A^{6} + 64 a_{4} - 64 a_{3}), T_{1} = 2 π,

30

R_{22} (t) = \frac{4}{T_{2}} \int_{0}^{\frac{T_{2}}{4}} R_{2} (t) \cos (ω t) d t = \frac{1}{128} A \times (48 a_{5} A^{2} + 40 a_{6} A^{4} + 35 a_{7} A^{6} + 64 a_{4}

- 64 ω^{2} a_{3} - 40 A^{4} ω^{2} a_{1} - 48 A^{2} ω^{2} a_{2}), T_{2} = \frac{2 π}{ω} .

Applying He’s frequency-amplitude formulation, we have:

31

ω^{2} = \frac{ω_{1}^{2} R_{22} (t) - ω_{2}^{2} R_{11} (t)}{R_{22} (t) - R_{11} (t)},

where $ω_{1} =$ 1 and $ω_{2} = ω$ . Finally, the amplitude-depended frequency can be approximated as:

32

ω_{A F F} = \frac{\sqrt{2}}{4} \frac{\sqrt{64 a_{4} + 48 a_{5} A^{2} + 40 a_{6} A^{4} + 35 a_{7} A^{6}}}{\sqrt{5 a_{1} A^{4} + 6 a_{2} A^{2} + 8 a_{3}}} .

Its approximate solution reads:

33

u (t) = A c o s (\frac{\sqrt{2}}{4} \frac{\sqrt{64 a_{4} + 48 a_{5} A^{2} + 40 a_{6} A^{4} + 35 a_{7} A^{6}}}{\sqrt{5 a_{1} A^{4} + 6 a_{2} A^{2} + 8 a_{3}}} t) .

6. Application of MMA

In this section, the MMA is applied to solve nonlinear sector. Eq. (2) can be rewritten in the following form:

34

\ddot{u} + (\frac{a_{1}}{a_{3}} u^{3} \ddot{u} + \frac{a_{2}}{a_{3}} u \ddot{u} + \frac{a_{4}}{a_{3}} + \frac{a_{5}}{a_{3}} u^{2} + \frac{a_{6}}{a_{3}} u^{4} + \frac{a_{7}}{a_{3}} u^{6}) u = 0 .

In addition, boundary conditions are considered. Here, if $u (t) = A c o s (ϖ t)$ be chosen as a trial function, then:

35

\frac{a_{4}}{a_{3}} < \frac{a_{1}}{a_{3}} u^{3} \ddot{u} + \frac{a_{2}}{a_{3}} u \ddot{u} + \frac{a_{4}}{a_{3}} + \frac{a_{5}}{a_{3}} u^{2} + \frac{a_{6}}{a_{3}} u^{4} + \frac{a_{7}}{a_{3}} u^{6}

< \frac{- a_{1} A^{4} ϖ^{2} - a_{2} A^{2} ϖ^{2} + a_{4} + a_{5} A^{2} + a_{6} A^{4} + a_{7} A^{6}}{a_{3}},

where $a_{4}$ is the minimum and $- a_{1} A^{4} ϖ^{2} - a_{2} A^{2} ϖ^{2} + a_{4} + a_{5} A^{2} + a_{6} A^{4} + a_{7} A^{6}$ is the maximum value of $\frac{a_{1}}{a_{3}} u^{3} \ddot{u} + \frac{a_{2}}{a_{3}} u \ddot{u} + \frac{a_{4}}{a_{3}} + \frac{a_{5}}{a_{3}} u^{2} + \frac{a_{6}}{a_{3}} u^{4} + \frac{a_{7}}{a_{3}} u^{6}$ .

Here the frequency value can be identified as follows:

36

ϖ^{2} = \frac{n}{(m + n)} \cdot \frac{- a_{1} A^{4} ϖ^{2} - a_{2} A^{2} ϖ^{2} + a_{4} + a_{5} A^{2} + a_{6} A^{4} + a_{7} A^{6}}{a_{3}} + \frac{m}{(m + n)} \cdot \frac{a_{4}}{a_{3}}

= \frac{k (- a_{1} A^{4} ϖ^{2} - a_{2} A^{2} ϖ^{2} + a_{5} A^{2} + a_{6} A^{4} + a_{7} A^{6})}{a_{3}} + \frac{a_{4}}{a_{3}},

where $m$ and $n$ are weighting factors, and $k = n / (m + n)$ . So the frequency can be approximated as follows:

37

ϖ = \sqrt{\frac{k (- a_{1} A^{4} ϖ^{2} - a_{2} A^{2} ϖ^{2} + a_{5} A^{2} + a_{6} A^{4} + a_{7} A^{6})}{a_{3}} + \frac{a_{4}}{a_{3}}} .

Then Eq. (24) can be rewritten as follows:

38

\ddot{u} + ϖ^{2} u = \ddot{u} + (\frac{a_{1}}{a_{3}} u^{3} \ddot{u} + \frac{a_{2}}{a_{3}} u \ddot{u} + \frac{a_{4}}{a_{3}} + \frac{a_{5}}{a_{3}} u^{2} + \frac{a_{6}}{a_{3}} u^{4} + \frac{a_{7}}{a_{3}} u^{6}) u + ρ,

where:

39

ρ = a_{3} (\frac{a_{1}}{a_{3}} u^{3} \ddot{u} + \frac{a_{2}}{a_{3}} u \ddot{u} + \frac{a_{4}}{a_{3}} + \frac{a_{5}}{a_{3}} u^{2} + \frac{a_{6}}{a_{3}} u^{4} + \frac{a_{7}}{a_{3}} u^{6}) u

+ (- k a_{1} A^{4} ϖ^{2} - k a_{2} A^{2} ϖ^{2} + a_{4} + k a_{5} A^{2} + k a_{7} A^{6}) u .

Combining $u (t) = A c o s (ϖ t)$ with $ρ$ , and using Fourier expansion series gives:

40

ρ (ϖ t) = \sum_{n = 0}^{\infty} δ_{2 n + 1} c o s [(2 n + 1) ϖ t] = δ_{1} c o s ϖ t + δ_{3} c o s 3 ϖ t + . . . ≅ δ_{1} c o s (ϖ t),

41

δ_{1} = (\frac{4}{π} \int_{0}^{\frac{π}{2}} ρ (ϕ) c o s (ϕ) d ϕ) = \frac{8}{315 π} (- 105 k a_{1} A^{4} ϖ^{2} - 105 k a_{2} A^{2} ϖ^{2} + 210 a_{4}

+ 105 k a_{5} A^{2} + 105 k a_{6} A^{4} + 105 k a_{7} A^{6} - 72 a_{1} A^{4} ϖ^{2} - 84 a_{2} A^{2} ϖ^{2} + 84 a_{5} A^{2}

+ 72 a_{6} A^{4} + 64 a_{7} A^{6}) .

In order to avoid secular term, the following equation can be set:

42

δ_{1} = 0 .

Then the following equation can be obtained:

43

k = \frac{2}{105} \frac{- 36 a_{1} A^{4} ϖ^{2} - 42 a_{2} A^{2} ϖ + 105 a_{4} + 42 a_{5} A^{2} + 36 a_{6} A^{4} + 32 a_{7} A^{6}}{A^{2} (- A^{2} a_{1} ϖ^{2} - a_{2} ϖ^{2} + a_{5} + A^{2} a_{6} + A^{4} a_{7})} .

Substituting Eq. (42) into Eq. (36), yields:

44

ϖ_{M M A} = \frac{\sqrt{3}}{3} \sqrt{\frac{84 a_{5} A^{2} + 64 a_{7} A^{6} + 72 a_{6} A^{4} + 105 a_{4}}{24 a_{1} A^{4} + 35 a_{3} + 28 a_{2} A^{2}}} .

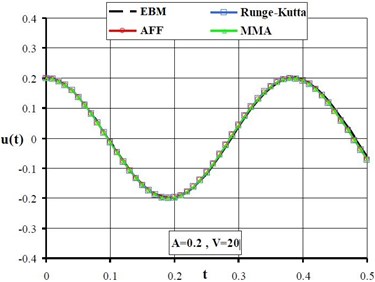
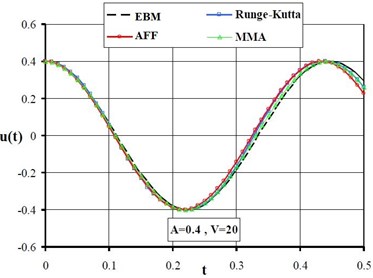
The answers of AFF method and max-min approach are plotted in Fig. 2. For comparison, results of energy balance [18] and numerical fourth-order Runge-Kutta method are plotted in these figures too. Herein the values of parameters are taken as $N =$ 15, $α =$ 10.

Fig. 2The results of MMA, AFF, EBM and Runge-Kutta method for A= 0.2 and 0.4, N= 15, α= 10

7. Conclusion

In this paper, the main purpose was to illustrate the application of amplitude frequency formulation (AFF) and max-min approach (MMA) in solving nonlinear oscillator arising in the microbeam based MEMS. Also, the capabilities and facile applications of these methods have been demonstrated in comparison with the numerical solution and energy balance method. By intensifying the value of voltage and initial condition A, it has been considered that the disagreement between the answers obtained by AFF, MMA and Runge-Kutta is very insignificant which indicates that these methods provide highly precise answers for nonlinear equations.

References

Lee S., Ramadoss R., Buck M., Bright V. M., Gupta K. C., Lee Y. C. Reliability testing of flexible printed circuit-based RF MEMS capacitive switches. Microelectronics Reliability, Vol. 44, Issue 2, 2004, p. 245-250.

Search CrossRef
Rhoads J. F., Shaw S. W., Turner K. L. The nonlinear response of resonant microbeam systems with purely-parametric electrostatic actuation. Journal of Micromechanics and Microengineering, Vol. 16, Issue 5, 2006, p. 890-899.

Search CrossRef
Kuehne I., Frey A., Marinkovic D., Eckstein G., Seidel H. Power MEMS – a capacitive vibration-to-electrical energy converter with built-in voltage. Sensors and Actuators A: Physical, Vol. 142, 2008, p. 263-269.

Search CrossRef
Czarnecki P., Rottenberg X., et al. Effect of substrate charging on the reliability of capacitive RF MEMS switches. Sensors and Actuators A: Physical, Vol. 154, 2009, p. 261-268.

Search CrossRef
Tocchio A., Langfelder G., Longoni A., Lasalandra E. In-plane and out-of-plane MEMS motion sensors based on fringe capacitances. Procedia Engineering, Vol. 5, 2010, p. 1392-1395.

Search CrossRef
Taghipor R., Akhlaghi T., Nikkar A. Explicit solution of the large amplitude transverse vibrations of a flexible string under constant tension. Latin American Journal of Solids and Structures, Vol. 11, 2014, p. 545-555.

Search CrossRef
Reza A., Sedighi H. M. Nonlinear vertical vibration of tension leg platforms with homotopy analysis method. Advances in Applied Mathematics and Mechanics, Vol. 7, 2015, p. 357-368.

Search CrossRef
Ghaffarzadeh H., Nikkar A. Explicit solution to the large deformation of a cantilever beam under point load at the free tip using the variational iteration method-II. Journal of Mechanical Science and Technology, Vol. 27, Issue 11, 2013, p. 3433-3438.

Search CrossRef
Nikkar A., Bagheri S., Saravi M. Dynamic model of large amplitude vibration of a uniform cantilever beam carrying an intermediate lumped mass and rotary inertia. Latin American Journal of Solids and Structures, Vol. 11, 2014, p. 320-329.

Search CrossRef
Sedighi H. M., Daneshmand F. Static and dynamic pull-in instability of multi-walled carbon nanotube probes by He’s iteration perturbation method. Journal of Mechanical Science and Technology, Vol. 28, Issue 9, 2013, p. 3459-3469.

Search CrossRef
Bagheri S., Nikkar A., Ghaffarzadeh H. Study of nonlinear vibration of Euler-Bernoulli beams by using analytical approximate techniques. Latin American Journal of Solids and Structures, Vol. 11, 2014, p. 157-168.

Search CrossRef
Bagheri S., Nikkar A. Higher order explicit solutions for nonlinear dynamic model of column buckling using variational approach and variational iteration algorithm-II. Journal of Mechanical Science and Technology, Vol. 28, Issue 11, 2014, p. 4605-4611.

Search CrossRef
Khan Y., Taghipour R., Falahian M., Nikkar A. A new approach to modified regularized long wave equation. Neural Computing and Applications, Vol. 23, 2013, p. 1335-1341.

Search CrossRef
Sedighi H. M., Daneshmand F. Nonlinear transversely vibrating beams by the homotopy perturbation method with an auxiliary term. Journal of Applied and Computational Mechanics, Vol. 1, Issue 1, 2014, p. 1-9.

Search CrossRef
Sedighi H. M., Daneshmand F., Abadyan M. Dynamic instability analysis of electrostatic functionally graded doubly-clamped nano-actuators. Composite Structures, Vol. 124, 2015, p. 55-64.

Search CrossRef
He J. H. Max-min approach to nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 9, Issue 2, 2008, p. 207-210.

Search CrossRef
He J. H. An improved amplitude-frequency formulation for nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 9, 2008, p. 211-212.

Search CrossRef
Fu Y., Zhang J., Wan L. Application of the energy balance method to a nonlinear oscillator arising in the microelectromechanical system (MEMS). Current Applied Physics, Vol. 11, 2011, p. 482-485.

Search CrossRef

About this article

Received

13 March 2015

Accepted

08 June 2015

Published

15 August 2015

SUBJECTS

Chaos, nonlinear dynamics and applications

Keywords

nonlinear oscillation

amplitude frequency formulation (AFF)

max min approach (MMA)

micro electro mechanical system

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.