Study of nonlinear dynamics of a particle on a rotating parabola by using efficient mathematical techniques

1. Introduction

Many phenomena exist in the environment where a particle's motion can be observed on them, such as centrifugation, centrifugal filters, industrial hopper, etc. Motion surface has different shapes especially for rotating application as it can be circular, parabolic or conical. On the other hand, the governing equations in most phenomena in applied sciences and engineering are nonlinear. In general, finding an exact or close-form solution for nonlinear problems is very difficult. So, with the rapid development of nonlinear science, there appears an ever-increasing interest of scientists in the analytical asymptotic techniques for nonlinear problems, and several analytical approximation methods have been developed; such as: homotopy perturbation method [1], variational iteration method [2], max-min approach [3], variational approach [4], Hamiltonian approach [5] and Laplace iteration method [6] .In recent years, these methods successfully applied arising in the applied sciences and engineering. For example; the vibrational behavior of quintic nonlinear in extensional beam on two-parameter elastic substrate based on the three mode assumptions is investigated by Sedighi [7]. He employed parameter expansion method to obtain the approximate expressions of nonlinear frequency-amplitude relationship for the first, second, and third modes of vibrations. A novel approach is applied to the analytic treatment of nonlinear fifth-order Equations by Saravi and Nikkar [8]. Ghaffarzadeh and Nikkar [9] applied a new analytical method called the variational iteration method-II (VIM-II) for the differential equation of the large deformation of a cantilever beam under point load at the free tip. Askari et al. [10] applied He’s energy balance method and He’s variational approach to frequency analysis of nonlinear oscillators with rational restoring force. Sedighi and Daneshmand [11] studied nonlinear transversely vibrating beams by the homotopy perturbation method with an auxiliary term. Barari et al. [12] studied non-linear vibration behavior of geometrically non-linear Euler-Bernoulli beams using variational iteration method and parameter perturbation method. Sedighi and Shirazi [13] presented a new asymptotic procedure to predict the nonlinear vibrational behaviour of classical micro-beams pre-deformed by an electric field using Parameter expansion method. Bagheri et al. [14] studied the nonlinear responses of clamped-clamped buckled beam. They used two efficient mathematical techniques called He’s variational approach and Laplace iteration method in order to obtain the responses of the beam vibrations. Salehi et al. [15] applied two efficient methods to consider large deformation of cantilever beams under point load. Younesian et al. [16] studied free oscillations of beams on nonlinear elastic foundations by VIM. Askari et al. [17] applied higher order Hamilton approach to nonlinear vibrating systems, and many other problems solved by these methods [18-21]. Recently, nonlinear dynamics of a particle on a rotating parabola are analyzed by means of the analytic and semi-analytic approaches by Mirzabeigy et al. [22].

The Variational Approach which is also called He’s variational approach, as well as the variational iteration method, was utilized here to obtain the analytical expression for the following model of nonlinear dynamics of a particle on a rotating parabola which introduced by Nayfeh and Mook [23]:

For validation of methods, we examine the advantages and disadvantages of applied methods by comparison of results with fourth-order Runge-Kutta solutions.

2. Basic concept of He’s variational approach

The variational approach to nonlinear oscillators was first proposed by Chinese mathemacian, Ji-Huan He [4]. We give a brief introduction of the method. To illustrate the method precisely, consider the following generalized nonlinear oscillations:

where $f\left(u\right)$ is a nonlinear function of $u$, $u\text{'}$ and $u\text{'}\text{'}$.

For simplicity, if function $f$ depends on $u$ only, its variational functional can be obtained as:

where $F$ is the potential, $dF/du=f$ and $T$ is the period of the nonlinear oscillator.

We assume that its approximate solution can be expressed as:

where $A$ and $\omega$ are the amplitude and frequency of the oscillator, respectively. Substituting Eq. (4) into Eq. (3), and setting $dJ/dA=0$, we can obtain an inexplicit amplitude-frequency relationship of Eq. (1).

3. Implementation of first order He’s variational approach

In this section, we solve Eq. (1) via variational approach. We can, now, easily obtain the following variational formulation:

Assume that its approximate solution can be expressed as:

where $\omega$ is the frequency to be determined and $A$ is the amplitude of oscillation. Substituting Eq. (6) into Eq. (5) results in:

Making $J$ stationary with respect to $A$, according to He’s method, we obtain:

Finally collocation at $\omega t=\pi /4$, the frequency can be approximated as:

and zero-order approximate solution from Eq. (22) is:

4. Basic concept of He’s variational iteration method

To clarify the basic ideas of He’s variational iteration method consider the following general differential equation:

where $L$ is a linear and $N$ is a nonlinear operator, $f\left(x\right)$ an inhomogeneous or forcing term. According to the variational iteration method, we can construct a correct functional as follows:

where $\lambda$ is a general Lagrange multiplier, which can be identified optimally via the variational theory, the subscript $n$ denotes the $n$th approximation, ${\tilde{u}}_n$ is considered as a restricted variation, i.e. $\delta {\tilde{u}}_n=$ 0.

For linear problems, its exact solution can be obtained by only one iteration step due to the fact that the Lagrange multiplier can be exactly identified. In this method, the problems are initially approximated with possible unknowns and it can be applied in non-linear problems without linearization or small parameters. The approximate solutions obtained by the proposed method rapidly converge to the exact solution.

5. Implementation of He’s variational iteration method

Now, for solving Eq. (1) by using VIM, first, we assume that the angular frequency of the system (1) is $\omega$, we have the following linearized equation:

So we can rewrite Eq. (1) in the form:

where $f\left(u\right)=({\epsilon }^2-{\omega }^2)u+4q^2{u}^2\ddot{u}+4q^{2}u{\dot{u}}^2=0$.

Applying the proposed method, the following iterative formula is formed as:

Its stationary conditions can be obtained as follows:

The Lagrange multiplier, therefore, can be identified as:

Substituting the identified multiplier into Eq. (15) results in the following iteration formula:

Assuming its initial approximate solution has the form:

And substituting Eq. (19) into Eq. (1) leads to the following residual:

By the Eq. (18), we can obtain:

In the same manner, the rest of the components of the iteration formula can be obtained. In order to ensure that no secular terms appear in $u_1$, resonance must be avoided. To do so, the coefficient of $\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$ in Eq. (20) requires being zero, i.e.:

6. Results and discussion

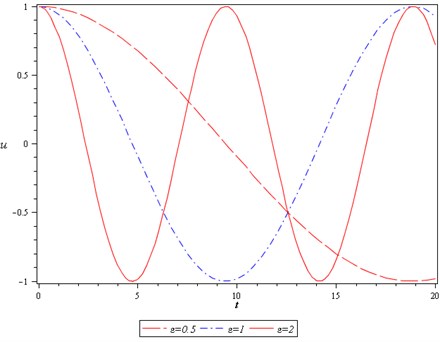
In this stage, we show the some figures to validation of the methods. In order to verify the precision of the presented methods, current results were compared with Runge-Kutta 4th order method, presented in Figs. 1, 2. It is observable that our results are in excellent agreement with the results provided by Runge-Kutta 4th order. Also, for show the effects of different parameters on the period, we presented Figs. 3, 4. We can see that period increases when value of the $\epsilon$ decreases or value of the $q$ increases and other parameters remain constant.

Fig. 1Comparison between the VIM, VA with the Runge-Kutta 4th order when ε= 1, q=A= 1

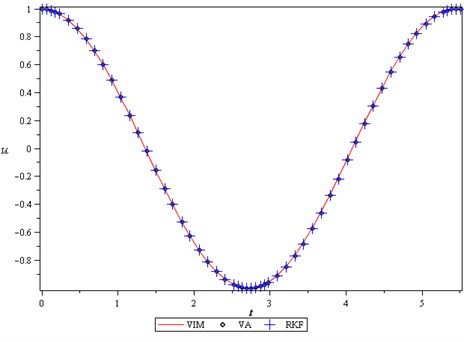
Fig. 2Comparison between the VIM, VA with the Runge-Kutta 4th order when ε= 1, q=A= 0.5

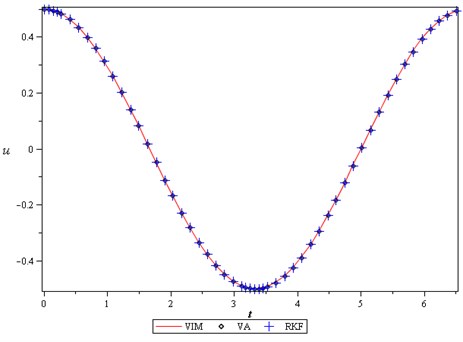
Fig. 3The effects of q on the period of motion when ε=A= 1

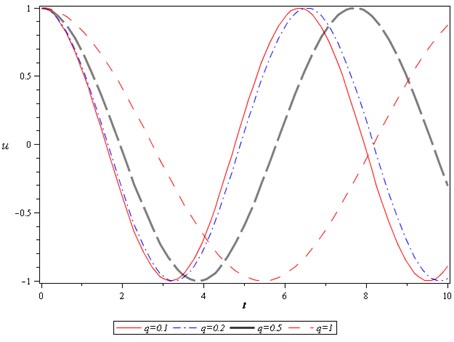
Fig. 4The effects of ɛ on the period of motion when q= 2 and A= 1

7. Conclusion

Study of nonlinear dynamics of a particle on a rotating parabola is main objective of this paper. We successfully applied two efficient and easy mathematical techniques called He’s variational iteration method and He’s variational approach to indicate the frequency-amplitude relationships. Comparison of results with numerical solutions are investigated. The performance and capability of applied methods are discussed by showing some figures.