Abstract
Regularization plays an important role in near-field acoustical holography (NAH), and determining an accurate regularization parameter is crucial to obtaining a meaningful solution. To choose better regularization parameters in the NAH based on equivalent source method (ESM), L-curve method, generalized cross validation (GCV) method and Hald empirical formula (HEF) method were compared at different source frequencies and holographic distances. The results show that the overall reconstruction precision and computational efficiency of HEF method is higher than GCV method and L-curve method, but the reconstruction precision of HEF method is slightly inferior to GCV method in the low and medium frequency. Further, a modified Hald empirical formula (MHEF) was proposed through exploring the relationship between the signal-to-noise ratio of measured sound pressure and the SNR value of HEF method. Then the HEF method, GCV method, and MHEF method were compared under different sound source positions, different measured sound pressure signal-to-noise ratios and different holographic array shapes, respectively. The results show that the reconstruction precision of MHEF method is the highest. Finally, an experiment was conducted to validate the correctness of the above conclusion.
1. Introduction
Noise source identification and quantification based on field measurements performed by a microphone array is a usual task in many fields of acoustical engineering. Several techniques such as NAH [1], beamforming [2] and inverse methods [3, 4] have been developed in order to tackle this problem. NAH is an advanced noise measurement and analysis technique for noise source identification and spatial sound field visualization. After more than thirty years, the holographic transform algorithm has achieved new breakthroughs, which is from the early NAH based on discrete Fourier transform (DFT) [1] to the NAH based on boundary element method (BEM) [3] and statistically optimal near-field acoustic holography (SONAH) [5], then to the NAH based on ESM [6]. Equivalent source method is derived from the wave superposition method based on simple source alternative which was proposed by Koopmann in 1989 [7]. Its basic principle is that the radiated sound field can be equivalent to the sound field superposition of a number of simple sources inside the radiation source. The ESM can be adapted to any form of sound source and array shape, at the same time has the ability to avoid the truncation, discrete and winding errors in the DFT [8], and also avoid the complex interpolation and singular integral treatment in the BEM [9]. With higher reconstruction precision and computational efficiency, the ESM has been widely studied and applied in recent years.
Because of the ill-posed inverse problem existing in the sound field reconstruction of ESM, measurement errors or environmental interference can cause the distortion of sound field reconstruction results. Therefore, in order to obtain the exact solution of the inverse problem, the regularization method should be utilized to reduce the ill-posed characteristic. The Tikhonov regularization method [10] is commonly adopted in the regularization process of ESM. And the main factor determining Tikhonov regularization effect is the regularization parameters selection. Without a priori noise information, regularization parameters are mainly determined by L-curve method [11] and GCV method [12]. With a priori noise information, regularization parameters are also determined by Morozov discrepancy principle (MDP) method [13], normalized cumulative periodogram (NCP) method [14] and Hald empirical formula (HEF) method [5]. Different regularization parameters determination methods have different influences on the sound field reconstruction precision, so a comparative study of the above regularization parameters determination methods is of great significance. Some scholars have explored it. In Ref. [15], based on planar NAH, the MDP method, GCV method and L-curve method were compared at different holography distances, source frequencies and signal-to-noise ratios, and the modified MDP method has achieved desired effect. Furthermore, the NCP method, GCV method and L-curve method were compared under inverse boundary element method (IBEM), SONAH and ESM by Gomes and Hansen [16]. The work presented in Ref. [16] shows that NCP method has poor performance than GCV method and L-curve method in the regularization process of ESM. In this paper, L-curve method, GCV method and HEF method are compared in the ESM and a modified Hald empirical formula is proposed. The simulations and experiment are conducted to validate the superiority of sound field reconstruction results of MHEF method.
The remainder of this paper develops as follows: first, in Section 2, the principle of ESM-based NAH is presented. Thereafter, in Section 3, the L-curve method, GCV method and HEF method are respectively illustrated and three methods are compared at different holography distances and source frequencies. Next, in Sections 4 and 5, the MHEF method is proposed and the HEF method, MHEF method and GCV method are compared under the different conditions. Then, in Section 6, the reconstruction results of L-curve method, GCV method, HEF method and MHEF method are compared based on a loudspeaker sound radiation experiment. Finally, Section 7 concludes the paper.
2. Theory
The key step of ESM-based NAH is to obtain the equivalent sources intensity, which can be solved by the measured sound pressure on holographic surface and the acoustic transfer function. The positional relationship between equivalent source surface, source surface, reconstruction surface and holographic surface is shown in Fig. 1. The holographic surface is shown in Fig. 2.
Fig. 1Diagram of ESM principle
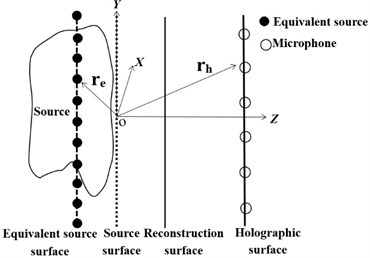
Fig. 2Holographic surface

The sound pressure of the point in the space is expressed as:
where is the column vector of equivalent source intensity; is transfer matrix between the equivalent source sequences and the sound pressure at the point.
In this paper, it has been assumed that measurement points are sampled by a microphone array and a set of equivalent sources are distributed on the source interior. The measured sound pressure on holographic surface can be expressed as:
where , is the column vector of measured sound pressure on holographic surface; is the transfer matrix between equivalent source sequences and measurement points, its expression is written as follow:
where is the density, Kg/m3; is sound velocity, m/s; is the wave-number, rad/m; is the distance vector between microphones and equivalent source sequence; is the distance vector from the th microphone on holographic surface to the source surface center (origin); is the distance vector from the th equivalent source to the source surface center.
The next step of ESM is to obtain the equivalent source intensity by the Eq. (2). In practice, the number of equivalent sources is larger than the number of measurement points, i.e. . This leads to an under-determined and ill-posed problem, and the solution of equivalent source intensity is not stable. Hence, the regularization method must be utilized in order to obtain a stable solution. In this paper, Tikhonov regularization method [10] is adopted and the regularization solution of equivalent source intensity is written as follow:
where the superscript “” represents the Hermitian transpose; is the regularization parameter; is the order identity matrix. The transfer matrix can be expressed by utilizing singular value decomposition (SVD):
where is a matrix containing singular values; and are the order and order unitary matrixes. Substituting Eq. (5) into Eq. (4), the regularization solution can be expressed as:
After the determination of equivalent source intensity, sound pressure of any point in the sound field can be calculated by the Eq. (1), so as to realize the entire sound field reconstruction.
3. Regularization parameters determination methods
When determining the Tikhonov regularization method, accurately obtaining regularization parameters is of great significance on improving the sound field reconstruction precision of ESM. In this section, regularization parameters were determined by L-curve method, GCV method and HEF method, and then the comparison of reconstruction precision of three methods was made.
3.1. L-curve method
The L-curve method, proposed by Hansen [11], is based on the long-known fact that a log-log parametric plot of , often has a distinct L-shape. The “corner point” of the L-curve defines an optimum value of regularization parameters. And the regularization parameter value of “corner point” can be obtained by solving maximum curvature of the L-curve. Due to its simplicity and intuitive appeal, the method has become popular in a number of application areas. But there are still some deficiencies. The work presented in Refs. [17, 18] indicates the L-curve corner may not even exist and L-curve does not have a strict convergence, leading to poor robustness of this method.
3.2. GCV method
The basic principle of GCV method is to construct a GCV function on the basis of the error model and regularization solution. The idea of GCV method in ESM is assuming that any one measurement point on holographic surface is not involved in the reconstruction calculation process, and sound pressure of the measurement point can be predicted accurately by the regularization solution of the resulting new model. The GCV function expression is given by:
where ; is the order identity matrix; represents the trace of a matrix. When taking the minimum value of GCV function, the corresponding regularization parameter is the optimum value. Ref. [19] indicates that GCV method has been observed to perform very well for reasonably large data sets with uncorrelated errors. However, it is known that for smaller data sets or correlated errors, the method is rather unstable, often resulting in under-smoothing. And the GCV function in Eq. (7) can be very flat near its minimum, it can have multiple local minima and the global minimum can be at the extreme endpoint.
3.3. HEF method
HEF method was applied in the regularization of SONAH [5]. In this paper, for the first time, it is used to determine regularization parameters in ESM, the formula is written as follow:
where is the wave-number, rad/m; is the distance between holographic surface and reconstruction surface, m; the recommended value of is the signal-to-noise ratio () of microphone sound pressure signals, dB. This method does not require a graph to select the optimum regularization parameter within a given range, but directly to determine regularization parameters by the known conditions. In SONAH, the sound field reconstruction results are stable, when regularization parameters are determined by this method [5, 20].
3.4. Comparison of three parameters determination methods
In order to compare the sound field reconstruction precision of ESM based on L-curve method, GCV method and HEF method, the reconstruction errors of three methods under different source frequencies and holographic distances were given in this section. The simulation conditions are as follows: taking the frequencies of 200-4000 Hz monopole point source for example, sound source is located at (0, 0, 0) m. Holographic surface is the Combo Array with the diameter of 0.65 m, which is shown in Fig. 2. The number of equivalent sources is 11×11 and equivalent sources are arranged evenly with the spacing of 0.02 m. Holographic distance () is 0.1-0.3 m and the distance between reconstruction surface and sound source is 0.05 m. The white Gaussian noise is added to microphone sound pressure with a signal-to-noise ratio of 50 dB. Hence, the value in Eq. (8) is 50 dB. Not special instructions, the following simulations are always the above simulation conditions. In this paper, the relative error () is introduced to evaluate the sound field reconstruction results; the expression of relative error [9] is as follow:
where the matrixes and represent the theory sound pressure values and corresponding reconstruction sound pressure values of the reconstruction surface, respectively; represents 2-norm of a vector. At the moment, the relative errors between the reconstruction results and theory results under three methods determining regularization parameters are shown in Fig. 3.
Fig. 3Reconstruction error curves based on L-curve method, GCV method and HEF method
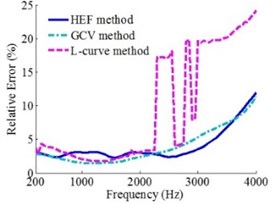
a)0.1 m
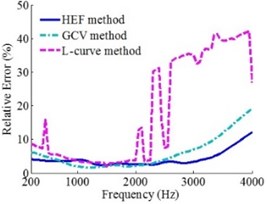
b)0.2 m
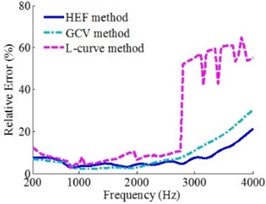
c)0.3 m
Fig. 3 shows that under the source frequencies of 200-4000 Hz and holographic distances of 0.1 m, 0.2 m and 0.3 m, the robustness of the reconstruction results based on HEF method and GCV method is much better than L-curve method. The reconstruction precision of all three methods is high in the low and medium frequency, but the GCV method is the highest. And when the frequencies are more than 2500 Hz, the reconstruction precision of HEF method is the highest. In addition, for this study, a 2.6 GHz Intel(R) Core(TM) i5-3230 M CPU was used to run the MATLAB programs. The single-frequency calculating time of L-curve method, GCV method and HEF method is 1.860 s, 2.037 s, 1.275 s, respectively.
To sum up: the robustness of reconstruction results based on HEF method and GCV method is much better than L-curve method. And the overall reconstruction precision and computational efficiency of the HEF method is higher than GCV method and L-curve method, but in the low and medium frequency, the reconstruction precision of HEF method is slightly inferior to GCV method, especially in the range of 400-1500 Hz.
4. Modification of the Hald empirical formula
Hald empirical formula is derived from the principle of SONAH, and the HEF method has good applicability in SONAH [20]. Known by the preceding analysis, the HEF method also has good applicability in ESM overall. But the reconstruction precision of this method is slightly inferior to GCV method in the low and medium frequency. In order to improve the reconstruction precision of this method in ESM, this section has further explored the Hald empirical formula. Under the given conditions, the wave-number and the distance between holographic surface and reconstruction surface are all constant in Eq. (8), while the value in the equation is only a recommended value that is the signal-to-noise ratio () of microphone sound pressure signals, so the optimum value is still uncertain. Hence, the relationship between the and the value of HEF method was firstly explored. Based on the foregoing simulation conditions, the holographic distance was set as 0.2 m and the was successively specified as 0-60 dB. When the value of was fixed, the value of Hald empirical formula at this time was successively specified as 0-60 dB. The contour maps of the relative errors under different and value are shown in Fig. 4. And the relationship between the and the optimum value of HEF method can be obtained from these contour maps.
Fig. 4Contour maps of the relative errors under different W and SNR value
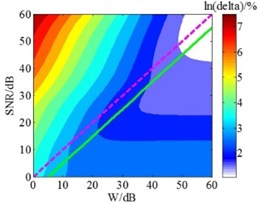
a) 200 Hz
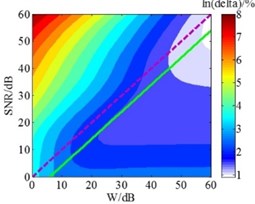
b) 500 Hz
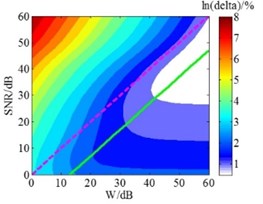
c) 1000 Hz
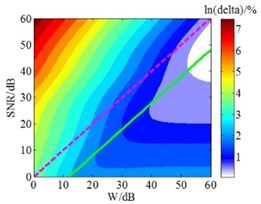
d) 1500 Hz
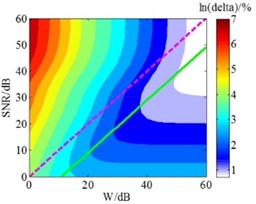
e) 2500 Hz
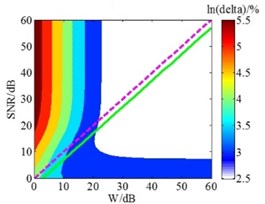
f) 4000 Hz
In Fig. 4, the is the relative error between reconstruction results and theory results; according to HEF method, dotted lines represent the recommended value which is equal to ; solid lines indicate the optimum value calculated in the simulation, which means the overall error is smallest. The Fig. 4 shows that when the frequencies are 200 Hz, 500 Hz, 1000 Hz, 1500 Hz, 2500 Hz and 4000 Hz, the optimum SNR values are smaller than the values 5 dB, 6 dB, 13 dB, 12 dB, 11 dB and 3 dB, respectively. Considering the entire frequency range, the relationship between the and the optimum at each frequency was obtained through further analysis. And the scatter plot was used fourth order polynomial curve fitting, the maximum residual modulus after the curve fitting is 6.82, which meets the precision requirements; the result is presented in Fig. 5.
Fig. 5Relationship of the frequency with the difference between W and optimum SNR
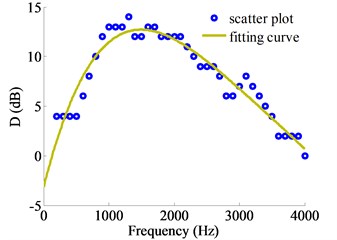
Fig. 5 shows that the relationship of frequency with the difference () between and optimum can be expressed as:
where is defined as the difference between and optimum , dB; is source frequency, Hz. On this basis, this paper proposed to modify the Hald empirical formula and the modified Hald empirical formula was given by:
where , dB; the remaining variables are the same ones in the Eq. (8).
5. Comparison of HEF method, MHEF method and GCV method
To validate the effectiveness that the MHEF method can improve the sound field reconstruction precision, the reconstruction errors of HEF method, MHEF method and GCV method were compared in this section under the conditions of different sound source positions, different measured sound pressure signal-to-noise ratios and different holographic array shapes, respectively. Because of the poor reconstruction precision and robustness, which has been discussed in the preceding analysis, the L-curve method is no longer compared in this section.
5.1. Comparison of three methods at different sound source positions
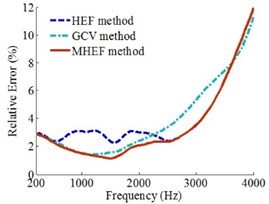
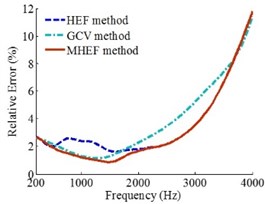
Based on the foregoing simulation conditions, when the sound source positions are at (0, 0, 0) m, (0.06, 0.06, 0) m and (0.09, 0.09, 0) m, three methods are compared. When the sound source position is at (0, 0, 0) m, the results are presented in Fig. 6.
Fig. 6 shows that when the sound source is at (0, 0, 0) m, the source frequencies are 200-4000 Hz and the holographic distances are separately specified as 0.1 m, 0.2 m and 0.3 m, the sound field reconstruction precision of MHEF method is higher than HEF method and GCV method in the entire frequency range. The reconstruction errors of MHEF method have been effectively improved in the low and medium frequency compared to the HEF method, especially in the range of 400-2500 Hz.
Fig. 6Error curves when source is at (0, 0, 0) m
a)0.1 m
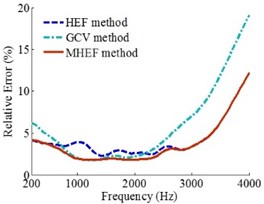
b)0.2 m
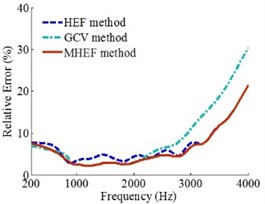
c)0.3 m
Fig. 7Error curves when source is at (0.06, 0.06, 0) m
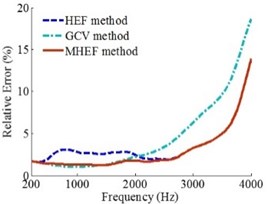
a)0.1 m
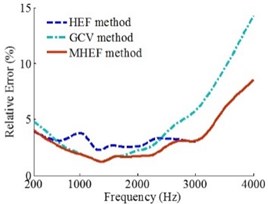
b)0.2 m
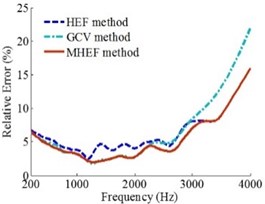
c)0.3 m
When the sound source positions are at (0.06, 0.06, 0) m and (0.09, 0.09, 0) m, the results are presented in Figs. 7 and 8, respectively.
Figs. 6, 7 and 8 show that when the sound source is at different positions, the source frequencies are 200-4000 Hz and the holographic distances are 0.1 m, 0.2 m and 0.3 m, the overall reconstruction precision of MHEF method is higher than HEF method and GCV method.
Fig. 8Error curves when source is at (0.09, 0.09, 0) m
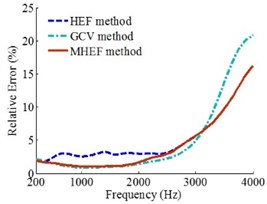
a)0.1 m
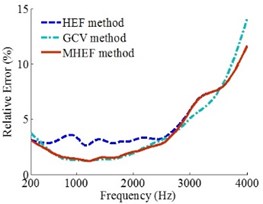
b)0.2 m
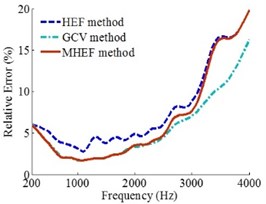
c)0.3 m
5.2. Comparison of three methods at different values of
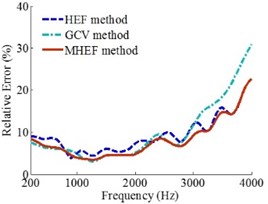
Based on the foregoing simulation conditions, three methods are also compared when the values of are 40 dB, 50 dB and 60 dB. When the value of is 50 dB, the analysis results are shown in Fig. 6. And when the values of are 40 dB and 60 dB, the analysis results are presented in Figs. 9 and 10, respectively.
Figs. 6, 9 and 10 show that when the values of are 50 dB, 40 dB and 60 dB, the source frequencies are 200-4000 Hz and the holographic distances are 0.1 m, 0.2 m and 0.3 m, the reconstruction precision of MHEF method is higher than HEF method and GCV method.
Fig. 9Error curves when the W is 40 dB
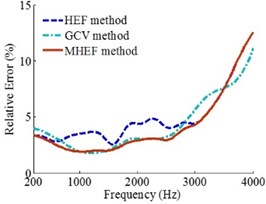
a)0.1 m
b)0.2 m
c)0.3 m
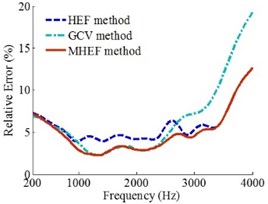
Fig. 10Error curves when the W is 60 dB
a)0.1 m
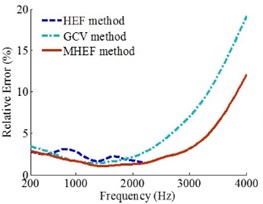
b)0.2 m
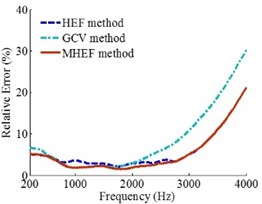
c)0.3 m
5.3. Comparison of three methods at different holographic array shapes
When holographic arrays are combo array, rectangular grid array and random arrangement circular array, the number of microphones on each array is equal and the effective array diameters are the same. The arranged forms of microphones on the rectangular grid array and random arrangement circular array are shown in Fig. 11. Based on the foregoing simulation conditions, the comparison of three methods was made. When holographic array is Combo array, the analysis results are shown in Fig. 6; and when holographic arrays are the rectangular grid array and random arrangement circular array, the analysis results are presented in Figs. 12 and 13, respectively.
Fig. 11Holographic array

a) Rectangular grid array

b) Random arrangement circular array
Figs. 6, 12 and 13 show that when holographic arrays are Combo array, rectangular grid array and random arrangement circular array, the source frequencies are 200-4000 Hz and the holographic distances are 0.1 m, 0.2 m and 0.3 m, the overall reconstruction precision of MHEF method is higher than HEF method and GCV method.
Fig. 12Error curves under rectangular grid array
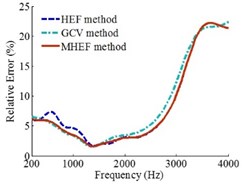
a)0.1 m
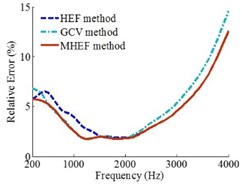
b)0.2 m
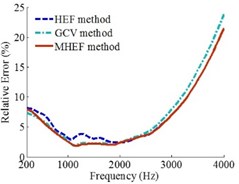
c)0.3 m
Fig. 13Error curves under random arrangement circular array
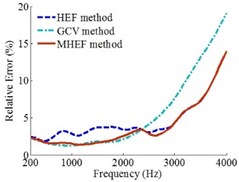
a)0.1 m
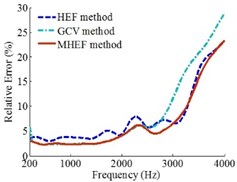
b)0.2 m
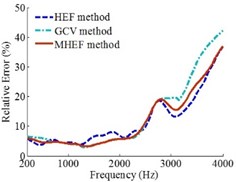
c)0.3 m
6. Validation experiment
In order to further validate the superiority of sound field reconstruction results of the MHEF method, an experiment with a loudspeaker located in a semi-anechoic chamber was conducted in this paper. Measurements were taken with the Brüel&Kjær 36-channel Combo Array at 0.1 m distance from the loudspeaker. The array has a diameter of 0.65 m and utilizes Brüel&Kjær Type 4951 microphones. Sound pressure signals received by microphones are acquired simultaneously by Brüel&Kjær 41-channel PULSE Type 3560D Data Acquisition System and then transferred to Brüel&Kjær PULSE LABSHOP Software where their cross-spectra are achieved. Eventually, through MATLAB programs, sound pressure signals are utilized to reconstruct the sound field where the distance between reconstruction surface and source surface is 0.05 m. The signal-to-noise ratio of microphone sound pressure signals measured in the experiment is about 40 dB. When source frequencies are 500 Hz, 1500 Hz and 2500 Hz, the measurement results at reconstruction location and the respective reconstruction results of L-curve method, GCV method, HEF method and MHEF method are shown in Fig. 14. The Fig. 15 shows the experimental site. In the experimental analysis frequency, the gaps of respective maximum sound pressure level (SPL) between the measurement results and reconstruction results at the reconstruction location are shown in Table 1; and the relative errors between measurement sound pressure values and reconstruction sound pressure values at the reconstruction location are presented in Fig. 16.
Table 1Gaps of maximum SPL between measurement results and reconstruction results
Frequency (Hz) | L-curve (dB) | GCV (dB) | HEF (dB) | MHEF (dB) |
300 | 0.94 | 2.12 | 0.88 | 0.64 |
500 | 2.59 | 0.43 | 1.64 | 0.36 |
800 | 0.67 | 0.49 | 0.93 | 0.48 |
1000 | 1.44 | 0.92 | 1.54 | 0.27 |
1500 | 0.66 | 0.68 | 1.53 | 0.34 |
2000 | 1.39 | 1.45 | 1.26 | 0.90 |
2500 | 0.95 | 1.03 | 0.85 | 0.54 |
3000 | 1.86 | 1.69 | 1.34 | 1.16 |
Fig. 14Experiment results
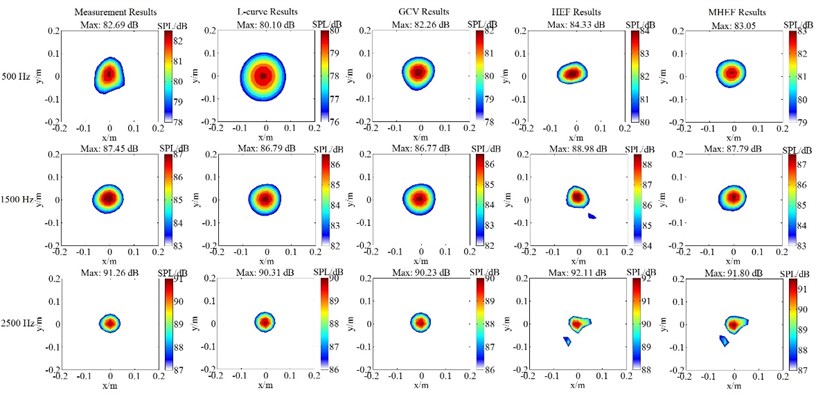
Fig. 15Experiment site

Fig. 16Relative errors of sound pressure value
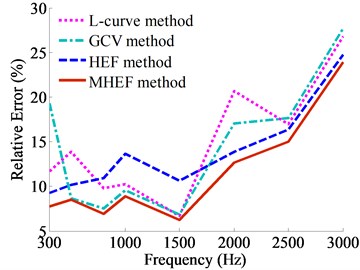
Fig. 14 shows that when the source frequencies are separately specified as 500 Hz, 1500 Hz and 2500 Hz, the reconstruction sound pressure contour plots of four regularization parameters determination methods can accurately achieve positioning of the sound source, and truthfully reflect the sound pressure values. Combined with the Fig. 14 and Table 1, in the frequencies of 300-3000 Hz, the gaps of maximum SPL between the measurement results and reconstruction results of MHEF method are the smallest among the four methods. In addition, from the Fig. 16, conclusion can be drawn that MHEF method acquires the highest sound field reconstruction precision with the smallest relative errors between the measurement sound pressure and reconstruction sound pressure. The experimental results have validated the correctness that the reconstruction precision of MHEF method is higher.
7. Conclusions
On the basis of the principle of ESM-based NAH, the regularization parameters determination methods of ESM-based NAH has been studied. First, the sound field reconstruction results are compared, whose regularization parameters are determined by L-curve method, GCV method and HEF method, respectively. The results show that the overall reconstruction precision and computational efficiency of HEF method is higher than GCV method and L-curve method, but the reconstruction precision of HEF method is slightly inferior to GCV method in low and medium frequency. The robustness of reconstruction results based on HEF method and GCV method is much better than L-curve method.
To improve the applicability of HEF method in ESM, the optimum value in Hald empirical formula is further explored. On this basis, a modified Hald empirical formula has been proposed to improve the sound field reconstruction precision. And the correctness that MHEF method can improve the sound field reconstruction precision has been validated under different sound source positions, different measured sound pressure signal-to-noise ratios and different holographic array shapes, respectively. Finally, an experiment is carried out to further validate the above conclusion. In a conclusion, the MHEF method not only inherits the advantages of HEF method such as good robustness, high computational efficiency and high reconstruction precision at high frequency, but also overcomes the deficiency of HEF method that the slightly poor reconstruction precision in the low and medium frequency, especially, the improvement has significant effect in the source frequencies of 400-2500 Hz.
References
-
Williams E. G., Maynard J. D., Skudrzyk E. Sound reconstruction using a microphone array. Journal of the Acoustical Society of America, Vol. 68, Issue 1, 1980, p. 340-344.
-
Chu Z. G., Yang Y. Comparison of deconvolution methods for the visualization of acoustic sources based on cross-spectral imaging function beamforming. Mechanical Systems and Signal Processing, Vol. 48, Issues 1-2, 2014, p. 404-422.
-
Kim B. K., Ih J. G. On the reconstruction of the vibro-acoustic field over the surface enclosing an interior space using the boundary element method. Journal of the Acoustical Society of America, Vol. 100, Issue 5, 1996, p. 3003-3016.
-
Kim Y., Nelson P. A. Optimal regularisation for acoustic source reconstruction by inverse methods. Journal of Sound and Vibration, Vol. 275, Issues 3-5, 2004, p. 463-487.
-
Hald J. Patch near-field acoustical holography using a new statistically optimal method. 32nd International Congress and Exposition on Noise Control Engineering, Jeju, Korea, 2003.
-
Leclere Q. Acoustic imaging using under-determined inverse approaches: frequency limitations and optimal regularization. Journal of Sound and Vibration, Vol. 321, Issues 3-5, 2009, p. 605-619.
-
Koopmann G. H., Song L., Fahnline J. A method for computing acoustic fields based on the principle of wave superposition. Journal of the Acoustical Society of America, Vol. 86, Issue 6, 1989, p. 2443-2438.
-
Williams E. G. Continuation of acoustic near-field. Journal of the Acoustical Society of America, Vol. 113, Issue 3, 2003, p. 1273-1281.
-
Valdivia N. P., Williams E. G. Study of the comparison of the methods of equivalent sources and boundary element methods for near-field acoustic holography. Journal of the Acoustical Society of America, Vol. 120, Issue 6, 2006, p. 3694-3705.
-
Tikhonov A. N. Solution of incorrectly formulated problems and the regularization method. Soviet Mathematics Doklady, Vol. 4, 1963, p. 1035-1038.
-
Hansen P. C., O’Leary D. P. The use of L-curve in the regularization of discrete ill-posed problems. SIAM Journal on Scientific Computing, Vol. 14, Issue 6, 1993, p. 1487-1503.
-
Golub G. H., Heat M., Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics, Vol. 21, Issue 2, 1979, p. 215-223.
-
Williams E. G. Regularization methods for near-field acoustical holography. Journal of the Acoustical Society of America, Vol. 110, Issue 4, 2001, p. 1976-1988.
-
Hansen P. C., Kilmer M. E., Kjeldsen R. H. Exploiting residual information in the parameter choice for discrete ill-posed problems. Bit Numerical Mathematics, Vol. 46, Issue 1, 2006, p. 41-59.
-
Li L. Z., Li J., Lu B. W. The determination of regularization parameters in planar near-field acoustic holography. Acta Acustica, Vol. 35, Issue 2, 2010, p. 169-178.
-
Gomes J., Hansen P. C. A study on regularization parameter choice in near-field acoustical holography. 7th European Conference on Noise Control, 2008, p. 2875-2880.
-
Bauer F., Lukas M. A. Comparing parameter choice methods for regularization of ill-posed problems. Mathematics and Computers in Simulation, Vol. 81, 2011, p. 1795-1841.
-
Hanke M. Limitations of the L-curve method in ill-posed problems. Bit Numerical Mathematics, Vol. 32, Issue 2, 1996, p. 287-301.
-
Lukas M. A. Robust GCV choice of the regularization parameter for correlated data. Journal of Integral Equations and Applications, Vol. 22, Issue 3, 2010, p. 519-547.
-
Hald J. Basic theory and properties of statistically optimized near-field acoustical holography. Journal of the Acoustical Society of America, Vol. 125, Issue 4, 2009, p. 2105-2120.
About this article
This work was supported by the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant No. CDJZR13110001).
