The substantiating of the dynamic parameters of the shaking conveyor mechanism

1. Introduction

The big application in various fields of the industry was received by the shaking conveyors applied to transportation of hot, poisonous, chemical aggressive cargoes by the supplement of complete tightness of their relocation [4], and also for transportation of the metallic cuttings damped with emulsion and oil, hot earth which has been beaten out from casting forms, small casting, foundry fusion mixture, etc. The shaking conveyor represents the chase hanged or supported to the fixed section. The chase commits oscillating motions hereupon the cargo which is in the chase, migrates concerning to the chase [5-8]. The nature of the flow and its parameters are determined by the nature of the oscillating committed by the chase. Shaking conveyors on the conditions of the chase flow and nature of cargo movement are subdivided on inertial (with variable and constant stress of cargo to the chase) in which [9] cargo under the influence of inertia force glides on the chase, and on vibrating in which cargo tears off the chase and migrates along the chase. The vibrating conveyors [1-3] are widely applied owing to a number of advantages in these latter days. The questions of the kinematic and dynamic study of the vibrating feeder intended for dosing of the fusion mixture loading of the melting furnaces of foundry production are considered in the presented work [11-15]. The principle of operation of the vibrating conveyor is described, and it is devoted the kinematic analysis of the action. The differential equation of the link move of the reduction of the vibrating conveyor is considered in the difference method (the approximate method) solutions of the equation of move of the vibrating conveyor is resulted [10]. It is devoted to the analysis of the equations solutions of conveyor move. Here tables of the results and relocation drawing and velocity of the leading link depending on time are resulted.

2. Materials and methods

2.1. Differential equations of the link move of the reduction of the vibrating conveyor

It is the action of the III class. The crew ВЕD basic crew from which there are three leads FЕ, АВ, GD. The link ОА is a leading link.

This action has one axis of motion, therefore relocation, velocities and speed-up of the driven link and action dots are functions of the relocation, velocities and speed-up of the leading link. Therefore we will find analytical dependences between relocations, velocities of the driven links and leading link. As the leading link enters into the rotational pair with the console we set function:

${\phi }_1={\phi }_1\left(t\right).$

Fig. 1Kinematic scheme of the shaking conveyor

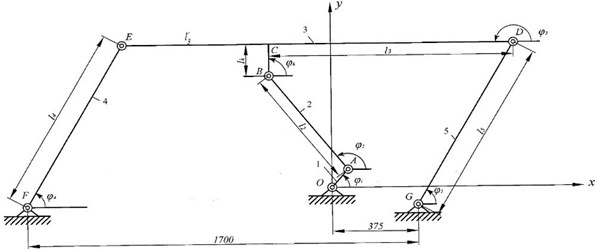
Table 1The action has following performances

No.	Links
	1	2	3	4	5
Mass, kg	$m_1=$30	$m_2=$65	$m_3=$ 1160	$m_4=$ 59	$m_5=$ 59
Length units, mm	$l_1=$60	$l_2=$430	$l_3=$ 1100	$l_4=$ 440	$l_5=$ 440

By the solution of the action move problem with one degree of freedom we will use the equation of the action move of the engine aggregate:

1

$I_k\left({\phi }_1\right)\frac{d{\omega }_1}{dt}+\frac{{\omega }_1^2}{2}\frac{d{{\rm I}}_k\left({\phi }_1\right)}{d{\phi }_1}=M_k-M_k.$

It is known to us dependence $M_P\left(\omega \right)$ and $M_R\left({\phi }_1\right)$. We determine $M_R\left({\phi }_1\right)$ the resulted moment of resistance forces from power equalling of the resulted moment of force resistance and the sum of powers of the moments [5] of resistance forces of operating in links $E$, $D$, $F$, $G$:

$M_K{\omega }_1=M_E^{}{\omega }_4+M_D^{}{\omega }_5+{М}_F^{}{\omega }_4+M_G^{}{\omega }_5,$
$M_K=M_E^{\mathrm{}}\frac{{\omega }_4}{{\omega }_1}+M_D^{\mathrm{}}\frac{{\omega }_5}{{\omega }_1}+M_F^{\mathrm{}}\frac{{\omega }_4}{{\omega }_1}+M_G^{\mathrm{}}\frac{{\omega }_5}{{\omega }_1}=M_E^{\mathrm{}}{u}_{41}+M_D^{\mathrm{}}{u}_{51}+M_F^{\mathrm{}}{u}_{41}+M_G^{\mathrm{}}{u}_{51}=4u_{41}{M}_k.$

Let’s find resulted moment of the flywheel actions ${{\rm I}}_k\left({\phi }_1\right)$ from equalling condition of kinematic energy of reduction link to the kinematic energy sum of all links of the action:

2

${{\rm I}}_k\left({\phi }_1\right)={{\rm I}}_{S1}+m_2{\vartheta }_{S2{\phi }_1}+{{\rm I}}_{S2}{u}_{22}^2+m_3{\vartheta }_{S3{\phi }_1}^2+\left({{\rm I}}_{4F}+{{\rm I}}_{5G}\right)l_{41}^2.$

We determine inertia moments of the first, second, fourth and fifth links.

${{\rm I}}_{S1}=m_1\cdot \frac{l_1^2}{2},{{\rm I}}_{S2}=m_2\cdot \frac{l_2^2}{2},{{\rm I}}_{4F}={{\rm I}}_{S4}+m_4\cdot {l^{\text{'}}}_4=m_4\cdot \frac{l_4^2}{2}+m_4\cdot \frac{l_4^2}{4},$
${{\rm I}}_{5G}={{\rm I}}_{S5}+m_5\cdot {l^{\text{'}}}_5=m_5\cdot \frac{l_5^2}{2}+m_5\cdot \frac{l_5^2}{4}.$

We differentiate the resulted inertia moment on ${\phi }_1$. For this purpose we substituted all above found values in the equation:

$\frac{d{{\rm I}}_k\left({\phi }_1\right)}{d{\phi }_1}=2m_2\sqrt{(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}{)}^2+(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}{)}^2}{\omega }_1$
$\cdot \frac{{\omega }_1\left[l_1\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1-\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1\right)+l_2^{\text{'}}{u}_{21}^2\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2-\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\right)+l_2^{\text{'}}\frac{d{u}_{21}}{d{\phi }_1}\left(\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2+\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2\right)\right]}{\sqrt{(\mathrm{l}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2^1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}{)}^2+(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2^1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}{)}^2}}+2I_{S2}\frac{l_1}{l_2}\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_4-{\phi }_1\right)}{\mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_2-{\phi }_4\right)}$
$\bullet \frac{l_1}{l_2}\left[\frac{u_{41}\cos \left({\phi }_4-{\phi }_1\right)\cdot \cos \left({\phi }_4-{\phi }_1\right)}{\sin \left({\phi }_4-{\phi }_2\right)}-\frac{\left[u_{21}\cos \left({\phi }_4-{\phi }_2\right)-u_{41}\cos \left({\phi }_4-{\phi }_2\right)\right]\cdot \sin \left({\phi }_4-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_4-{\phi }_2\right)}\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+2m_3{\mathrm{\omega }}_1^2\left[\begin{array}{c}-l_1\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1\right)-l_2\cdot u_{21}^2\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2-\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\right)+l_2\frac{d{u}_{21}}{d{\phi }_1}\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2-\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\right)\\ -\frac{\left[\cos \left({\phi }_1-{\phi }_2\right)\cdot u_{21}-\cos \left({\phi }_1-{\phi }_2\right)\right]\cdot \sin \left({\phi }_2-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}\end{array}\right]\cdot \frac{l_1}{l_4}\frac{\sin \left({\phi }_2-{\phi }_1\right)}{\sin \left({\phi }_2-{\phi }_4\right)}$
$=2m_2{\omega }_1^2\left[l_1\left(cos{\phi }_1-sin{\phi }_1\right)+l_2^{\text{'}}{u}_{21}\cdot \left(cos{\phi }_2-sin{\phi }_2\right)+l_2^{\text{'}}\frac{d{u}_{21}}{d{\phi }_1}\left(sin{\phi }_2+cos{\phi }_2\right)\right]+2{{\rm I}}_{S2}$
$\cdot \frac{l_1^2}{l_2^2}\frac{\sin \left({\phi }_4-{\phi }_1\right)}{\sin \left({\phi }_2-{\phi }_4\right)}\left[\frac{u_{41}\cos \left({\phi }_1-{\phi }_4\right)-\cos \left({\phi }_4-{\phi }_1\right)}{\sin \left({\phi }_2-{\phi }_4\right)}-\frac{\left[u_{21}\cos \left({\phi }_4-{\phi }_2\right)-u_{41}\cos \left({\phi }_4-{\phi }_2\right)\right]\sin \left({\phi }_4-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_4-{\phi }_2\right)}\right]$
$-2m_3{\omega }_1^2\left[l_1\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1\right)+l_1^{\text{'}}{u}_{21}^2\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2-\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\right)-l_2\frac{d{u}_{21}}{d{\phi }_1}\left(\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2-\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2\right)-\frac{d{u}_{51}}{d{\phi }_1}\left(a\mathrm{c}\mathrm{o}\mathrm{s}{\omega }_{5}t-b\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{5}t\right)\right]$
$+2({{\rm I}}_{4F}+{{\rm I}}_{5G})\cdot \frac{l_1^2}{l_4^2}\frac{\mathrm{s}\mathrm{i}\mathrm{n}({\phi }_2-{\phi }_1)}{\mathrm{s}\mathrm{i}\mathrm{n}({\phi }_2-{\phi }_4)}$
$\cdot \left\{\frac{u_{21}\cos \left({\phi }_1-{\phi }_2\right)-\cos \left({\phi }_1-{\phi }_2\right)}{\sin \left({\phi }_2-{\phi }_4\right)}-\frac{\left[u_{21}\cos \left({\phi }_1-{\phi }_2\right)-\mathit{cos}\left({\phi }_1-{\phi }_2\right)\right]\cdot \sin \left({\phi }_2{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}\right\}.$

The move equation of the reduction link of the action looks like:

3

${{\rm I}}_{S1}+m_2{\omega }_1^2\left[\right(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}{)}^2+\left(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2^{\text{'}}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}{)}^2\right]+{{\rm I}}_{S2}\frac{l_1^2}{l_2^2}\frac{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_4-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}$
$+m_3{\omega }_1^2\left[(-l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}+a{u}_{51}\mathrm{c}\mathrm{o}\mathrm{s}{\omega }_{5}t{)}^2+(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}-b{u}_{51}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{5}t{)}^2\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\left({{\rm I}}_{4F}+{{\rm I}}_{5G}\right)\frac{l_1^2}{l_4^2}\frac{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}\frac{d{\omega }_1}{dt}$
$+\frac{{\omega }_1^2}{2}\left\{2m_2{\omega }_1^2\left[(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2^{\text{'}}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21})\left(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1{u}_{21}^2+{l^{\text{'}}}_2\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\frac{d{u}_{21}}{d{\phi }_1}\right)\right.\right.$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\left.-\left(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2^{\mathrm{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}\right)\left(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2^{\mathrm{\text{'}}}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}^2-l_2^{\mathrm{\text{'}}}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2\frac{d{u}_{21}}{d{\mathrm{\phi }}_1}\right)\mathrm{}\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+2{{\rm I}}_{S2}\frac{l_1^2}{l_2^2}\left[\frac{\left(\cos \left({\phi }_1+{\phi }_4\right)-\cos \left({\phi }_1+{\phi }_4\right)\right)\sin \left({\phi }_1-{\phi }_4\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+2m_3{\omega }_1^2\left[\begin{array}{c}\left(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1+l_2\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}-a{u}_{51}\mathrm{c}\mathrm{o}\mathrm{s}{\omega }_{5}t\right)\left(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}^2+l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2\frac{d{u}_{21}}{d{\mathrm{\phi }}_1}-a\mathrm{c}\mathrm{o}\mathrm{s}{\omega }_{5}t\frac{d{u}_{51}}{d{\mathrm{\phi }}_1}\right)\\ -\left(l_1\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_1+l_2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2{u}_{21}-b{u}_{51}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{5}t\right)\left(l_1\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_1-l_2\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_2{u}_{21}^2-l_2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_2\frac{d{u}_{21}}{d{\phi }_1}+b\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{5}t\frac{d{u}_{51}}{d{\phi }_1}\right)\end{array}\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\left.2\left({{\rm I}}_{4F}+{{\rm I}}_{5G}\right)\frac{l_1^2}{l_2^2}\frac{\left[\cos \left({\phi }_1+{\phi }_2\right)-\cos \left({\phi }_1-{\phi }_2\right)\right]\sin \left({\phi }_2-{\phi }_1\right)}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left({\phi }_2-{\phi }_4\right)}\right\}={\mathrm{М}}_{k_{\mathrm{o}}}-\alpha {\omega }_1-4u_{41}\left({M^{\text{'}}}_k+K_0{\phi }_5\right).$

For solution of the Eq. (3) there are following initial conditions: at $t=$0, ${\omega }_1=$0, ${\phi }_1=$60°.

3. Results and discussion

A proper dynamic model has been developed within MSC ADAMS software to provide information on the feasibility of the proposed design solution. Simulation tests have been carried out and results are discussed for validating the proposed design and characterizing its operation.

Fig. 2Six bar linkage motion simulation in MD Adams

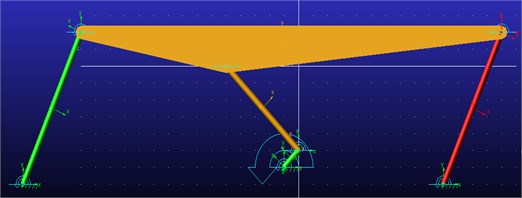
Fig. 3Computed plot of the force and momentum joint 1

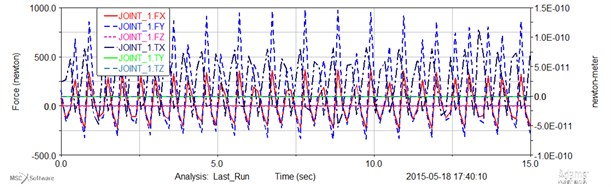
Fig. 4Computed plot of the force and momentum joint 2

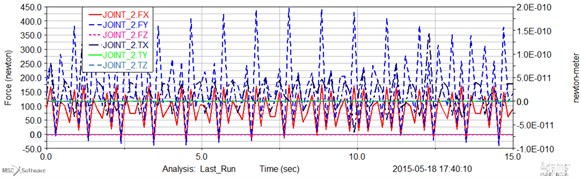
Fig. 5Computed plot of the force and momentum joint 3

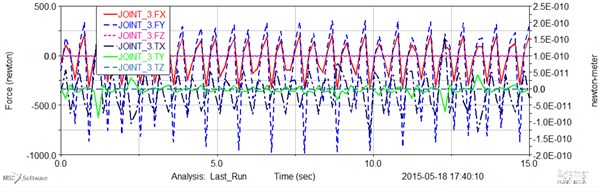
Fig. 6Computed plot of the force and momentum joint 7

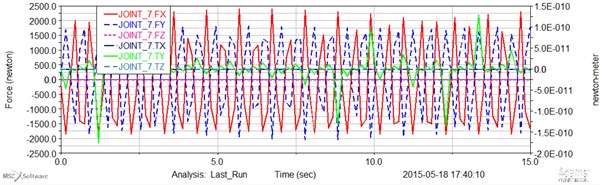
Fig. 7Computed plot of the force and momentum joint 8

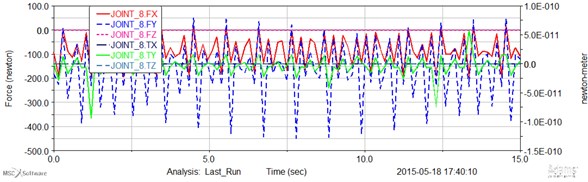
Fig. 8Computed plot of the force and momentum joint 9

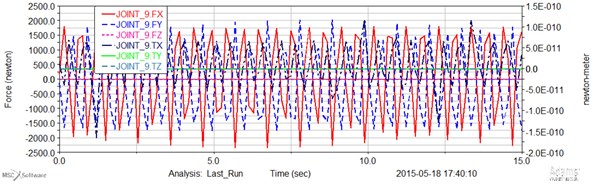
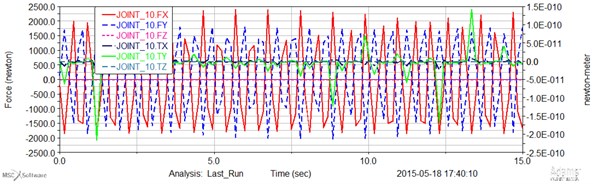
Fig. 9Computed plot of the force and momentum joint 10

4. Conclusions

1) Formulas for the position determination and velocity of conducted links depending on position and velocity of the leading link are received.

2) The differential equations of the link move of the action reduction are received.

3) On the basis of the profiles variation analysis of the angular rate of the leading link it is possible to make the following concluding:

– with the growth of the starting driving moment middle angulator of the action grows;

– with reduction of the starting driving moment middle angular rate of the action is decays;

– with coefficient increase ${\alpha }_0$, ${\omega }_{cp}$ grows.

4) The basis of the program MSC Adams software investigated the kinetic energy and translational momentum of each link mechanism with results and calculations.