Damage detection of wind turbine supporting structures using an improved harmony search algorithm

Jahjouh, Mahmoud M.; Nackenhorst, Udo

Vibroengineering Procedia

Browse Procedia

Published: 09 October 2015

Check for updates

Damage detection of wind turbine supporting structures using an improved harmony search algorithm

Mahmoud M. Jahjouh¹

Udo Nackenhorst²

^{1, 2}Institute of Mechanics and Computational Mechanics (IBNM), Leibniz Universität Hannover, Hanover, Germany

Corresponding Author:

Mahmoud M. Jahjouh

Cite the article Download PDF

Downloads 1216

Abstract

Offshore Wind Energy Conversion Devices (OWECDs) are sensitive structures subjected to high force fluctuations making them prone to damage and present a challenge for in-situ structural identification due to the rough environment of offshore locations. Thus a remote identification and damage detection technique is required to keep track of any significant changes to the structural parameters of the OWECD. It is intended to present a structural identification and damage detection scheme using a Modified Adaptive Harmony Search coupled with a Modified Search Space Reduction Method (MAHS-MSSRM) to determine the structural stiffness of a damaged supporting structure of a numerically modeled OWECD based on its vibration response. The studied OWECD is an idling baseline 5-MW reference wind turbine developed by the National Renewable Energy Laboratory (NREL) identified under varying degrees of noise and different sensor configurations. The resulting identification accuracy and robustness were satisfying and encourage further investigation of the identification scheme with multiple damage locations, smaller damage values and unaligned inflow winds.

1. Introduction

Structural identification and damage detection plays an important role in Structural Health Monitoring (SHM), in which the current state of a structure is assessed and compared, if possible, to an initial state to detect damage.

The construction of wind turbines in offshore environments brings new complexity to the problem in the form of additional sources of loading, harder construction practice, more complex inspection and faster degradation due to the aggressive marine environment.

Since an inspection of an OWECD can prove to be costly, wind turbine manufacturers, owners and operators could benefit from a remote SHM, which utilizes vibration response measurements to detect damage and, if required, lead investigation teams for effective repairing.

Generally, damage is a change introduced to any structural characteristic that adversely affects the current or future performance of the structure [1]. In the context of this contribution, it is considered the decrease in the structural stiffness of the supporting structure. When identifying damage, four levels exist based on the information they provide about the structural damage [2]. These are as follows: Level I – Detection, Level II – Location, Level III – Quantification and Level IV – Prediction of remaining service life.

With the advances in sensor technology and computational power, interest in structural identification has grown significantly in recent literature. This can be observed in special issues such as the Journal of Engineering Mechanics [3, 4], Computer-Aided Civil and Infrastructure Engineering [5], Smart Materials and Structures [6] and Structures and Infrastructure Engineering [7].

A variety of structural identification and damage detection techniques have been applied to different structures ranging from as simple as beams to as complicated as bridges. A general review of structural identification methods and their application to various structures is documented in [1, 8, 9]. Furthermore, a review to damage detection techniques and condition monitoring applied on wind turbines is provided in [10, 11].

Amongst other damage detection methods, vibration based approaches are considered the most common damage detection methods used. These approaches rely on the measurement of the response of structures from applied excitation, and the extraction of structural features from those to determine the current structural parameters, and ultimately, structural damage. Damage in blades was identified in [12-14]. OWECDs supporting structures were considered in [15-17].

Yet, some of these studies were sometimes inconclusive, didn't consider noise and/or relied on the change of modal characteristics to detect damage while utilizing classical methods for feature extraction. Classical methods, at their best performance, still are less effective than non-classical methods based on optimization algorithms [18]. Furthermore, structural identification based on modal characteristics and frequency changes is not always advantageous. Structural frequency variation due to changes in environmental and operational conditions is sometimes more than the changes due to structural damage, as reported in [19].

It is intended in this contribution to present an improved harmony search algorithm that is used in the structural identification and damage detection of numerically modeled OWECDs utilizing its vibration response. It is sought to achieve a detection of Level (III). A variety of noise values is applied to the vibration response and different sensor configurations are considered. Damage considered here is in the form of stiffness reduction of one of the nodes.

2. Modeling of OWECDs

For the identification problems studied, a 5-MW reference wind turbine for offshore system development, developed by the National Renewable Energy Laboratory (NREL) [20], is considered. For the structural analysis of the turbine, an open source analysis program called FAST (Fatigue, Aerodynamics, Structures and Turbulence), also developed by NREL, is used. The accuracy and adequacy of the FAST code was tested and proven in an offshore code comparison report OC3 [21] and OC4 [22].

In modeling an OWECD, several aspects of the turbine are considered and coupled by FAST. These are: (1) The aerodynamic analysis of wind and blades, (2) The control systems in terms of pitch, yaw, etc., (3) The hydrodynamic analysis of currents and waves, (4) The structural response of the turbine components.

A summary of information with regard to the turbine considered, its operational status and environmental conditions are summarized in Table 1, whereas a schematic is shown in Fig. 1. Any other information not mentioned in Table 1 is taken “as is” from [20].

Table 1Key aspects of considered OWECDs

Aspect	Value/explanation
Number of nodes in supporting structure	15, equally spaced
Length of wind history	10 seconds
Time step for analysis	0.02 seconds
Mean wind speed	15 m/s
Wind field	Turbulent
Yaw error	0 degrees, mainly downwind motion assumed
Status of turbine	Idling (i.e. RPM ≈ 0)
Damage location	Node 5
Damage magnitude	10 % downwind stiffness reduction
Measured response	Tower downwind acceleration
Sensor location (nodes)	Scenario 1: (15) Scenario 2: (02, 04, 08, 12 and 15) Scenario 3: (02, 03, 04, 05, 06, 08, 10, 12 and 15)

3. Formulating the optimization problem

3.1. Solution vector and search space

Since it is assumed that the tower is facing wind directly, downwind motion is dominant and the identification problem is limited to the downwind stiffness parameters. Recalling that the supporting structure was discretized using 15 equally spaced nodes, 15 unknown stiffness variables are required to describe the supporting structure. These variables are sorted in the solution vector as follows:

1

X = \{k_{1}, k_{2}, \dots, k_{15}\} .

Each stiffness variable is bounded by upper and lower bounds, and has a defined step size. Thus, for a stiffness parameter $k_{i}$ the following relation holds true:

2

k_{i} \in \{k_{i}^{l}, k_{i}^{l} + k_{i}^{s s}, k_{i}^{l} + 2 k_{i}^{22}, \dots, k_{i}^{u}\},

where $k_{i}^{l}$ , $k_{i}^{u}$ , $k_{i}^{s s}$ are the lower bound, upper bound and step size of variable $k_{i}$ , respectively. Given the number of variables, bounds and step sizes, a measurement of the overall complexity of the problem, namely: the search space size ( $N_{S S}$ ) can be calculated:

3

N_{S S} = \prod_{i = 1}^{15} (\frac{k_{i}^{u} - k_{i}^{l}}{k_{i}^{s s}} + 1) .

3.2. The objective function

Optimization algorithms perform an iterative search to obtain the maximum/minimum of a function called: The objective function. In the context of structural identification, a minimization problem can be constructed, with aim to minimize errors between the predicted response ${\ddot{x}}_{p}$ from a trial solution vector $X$ and the measured response ${\ddot{x}}_{r}$ from the structure being identified.

Thus, the objective is to find $X$ that minimizes the unconstrained objective function $F (X)$ where $X \in Search Space,$ and:

4

F (X) = \frac{1}{t_{t o t a l}} \frac{1}{n_{s}} \sum_{t = 0}^{t_{t o t a l}} \sum_{i = 1}^{n_{s}} \sqrt{{[{\ddot{x}}_{p} (i, t) - {\ddot{x}}_{r} (i, t)]}^{2}},

where $t_{t o t a l}$ is the total time history under consideration, $n_{s}$ is the number of sensors.

4. The MAHS-MSSRM algorithm

4.1. The modified adaptive harmony search (MAHS)

The optimization algorithm used in this contribution is a modified version of the Harmony Search (HS) algorithm. HS is a powerful optimization algorithm developed by Geem et al. [23], which is inspired by the efforts of musicians to find the best notes to play. HS is more efficient, faster and easier in implementation than other well-known algorithms such as the Genetic Algorithm (GA) [24].

Being a flexible optimization algorithm, several improvements and modifications were applied to the basic HS. An overview of these modifications can be found in [25].

An adaptive HS (AHS) was proposed by Hasancebi et al. [26]. In the AHS, the control parameters change dynamically, increasing convergence and performance of the algorithm.

An additional modification presented by the authors in [27] in the form of a so-called “local effect” is implemented, thus resulting in the Modified Adaptive Harmony Search algorithm (MAHS). The introduction of local effect was motivated by the fact that stiffness variables of structures are coupled with each other. A flowchart of MAHS can be found in [27].

4.2. The modified search space reduction scheme (MSSRM)

A modified search space reduction method (MSSRM) has been suggested by the authors in [27] based on the original SSRM developed in [18].

Originally, the performance of the optimization algorithm is enhanced by reducing the search space prior the start of an optimization run based on the results of the previously made runs. Thus after reaching a certain number of runs, the standard deviation and mean values for each variable in the solution vectors obtained so far are calculated. Finally, the bounds are redefined as follows:

5

k_{i}^{b} = μ_{i} \pm b \times σ_{i},

where $μ_{i}$ and $σ_{i}$ are the mean value and standard deviation of the $i$ th variable in the optimum solution vectors obtained from the runs carried out, $b$ is a constant and $k_{i}^{b}$ is the upper or lower bound of $k_{i}$ .

In the MSSRM, however, the search space is reduced twice, once before starting the run by utilizing the SSRM, and once within the run. Within the run, the limits are changed after reaching a number of iterations based on the results so far stored in the Harmony Memory (the storage system of the harmony search algorithm). The equation to do so is similar to Eq. (6), but now $μ_{i}$ and $σ_{i}$ are calculated based on the solutions inside the Harmony Memory. A flowchart of MAHS coupled with MSSRM can be found in [27].

5. Structural identification and damage detection of OWECDs

As previously mentioned, a 5-MW reference wind turbine is considered. The downwind stiffness values are identical to those defined in [20]. Damage is applied in form of stiffness reduction by 10 % at node 5. The initial upper bounds were the stiffness values of the healthy structure (undamaged), the initial lower bounds were half the upper bounds, and the step size was 1 % of the upper bounds. Thus creating 51 possible values for each variable in the solution vector and a search space of $N_{S S} =$ 4.1×10²⁵.

To further simulate real response measurements, noise is applied to the original response as a percentage of the Root Mean Square (RMS) of the response signal. Furthermore, different sensor configurations were studied.

For each configuration, 5 structural identification tests were performed, having a total of 16000 iterations. Each test is divided into 8 subruns, each subrun having 2000 iterations. Iteration level search space reduction starts at 10 % of the maximum iterations, i.e. at iteration no. 200. Subrun level search space reduction starts at the 4th subrun. The MAHS-MSSRM control parameters were taken from [27].

Fig. 1Schematic of the considered baseline 5-MW OWECD

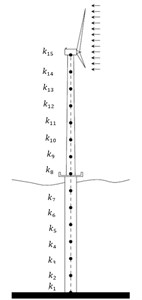
Fig. 2Typical convergence history

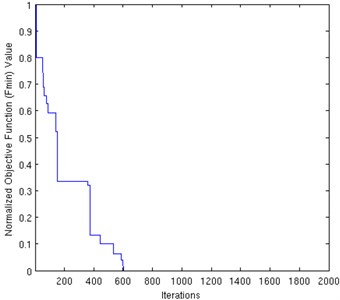
A typical variation of the normalized objective function for the best run is shown in Fig. 2. The objective function is normalized relative to the objective function value obtained in the first iteration.

6. Results of identification

The average results of all identification runs performed on several sensor and noise setups are summarized in Table 2.

The obtained results for noise levels up to 5 % are quite satisfactory, yet some less satisfying performance was obtained at extreme noise levels of 10 %. Furthermore, the accuracy of the results improves as more sensors are attached to the structure to help determine the damage location as well as averaging the noise out.

Table 2Identification results

Sensor scenario	Noise (%)	Mean error (%)	Identified damage of node No.
Sensor scenario	Noise (%)	Mean error (%)	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	0	0	0	0	0	0	10	0	0	0	0	0	0	0	0	0	0
	2	0.51	0	0	0	0	11	1.6	2.8	0.4	0	0	0	0	0	0.2	1.6
	5	1.72	0.2	0	0	0	1.8	5.4	8.2	0	0	0	0	0	1.6	0.6	1.6
	10	3.53	0	0	0	0.2	0	27	10	0.2	0.6	0.4	0	0	0.8	3.0	0.8
2	0	0	0	0	0	0	10	0	0	0	0	0	0	0	0	0	0
	2	0.27	0	0	0	0.4	9.0	1.4	0	0	0	0	0	0	0	0.4	0.8
	5	0.32	0	0	0	0	12	0.6	1.8	0	0	0	0	0	0	0.2	0.2
	10	1.32	0	0	0	0	6.0	5.6	1.8	0	0	0.2	0	0.2	1.0	1.6	5.4
3	0	0	0	0	0	0	10	0	0	0	0	0	0	0	0	0	0
	2	0.16	0	0	0	0	9.2	0	1.2	0	0	0	0	0	0	0.2	0.2
	5	0.24	0	0	0	0	8.6	0.4	0.6	0	0	0	0	0	0.4	0.4	0.4
	10	1.0	0	0	0	0	5.8	1.8	4.2	0.2	0.2	0	0	0	0	1.6	1.0

7. Conclusion

This contribution used an enhanced version of the adaptive harmony search algorithm in the structural identification of OWECDs supporting structures. The enhancements are in the form of the introduction of a “local effect” and the hybridization with a modified search space reduction method, thus resulting in the MAHS-MSSRM.

The satisfying performance of MAHS-MSSRM has been proven by numerical examples of a 5-MW baseline turbine analyzed by an open source code called FAST. MAHS-MSSRM achieved (at 0 % noise) a 100 % identification accuracy. Satisfying results were obtained at noise levels as high as 5 %, and less satisfying results were obtained at extreme noise levels of 10 %.

It is always beneficiary to include a noise filtering subroutine when dealing with noise contaminated input data. The inclusion of such subroutine would decrease the effective noise percentage, thus improving the performance of the structural identification and damage detection algorithm.

The results obtained encourage further investigation of the effect of different damage magnitudes, multiple damage locations as well as on-line wind turbine identification. Furthermore, identification of soil structure interaction is also a promising research fields.

References

Sohn H., Farrar C., Hemez F. A Review of Structural Health Monitoring Literature: 1996-2001. Technical Report, Los Alamos National Laboratory (LANL), Los Alamos, NM, 2004.

Search CrossRef
Rytter A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg, 1993.

Search CrossRef
Ghanem R., Sture S. Special issue: structural health monitoring. Journal of Engineering Mechanics ASCE, Vol. 126, 2000.

Search CrossRef
Bernal D., Beck J. Special issue on phase I of the IASC-ASCE structural health monitoring. Journal of Engineering Mechanics ASCE, Vol. 130, 2004.

Search CrossRef
Adeli H. Special issue: health monitoring of structures. Computer-Aided Civil and Infrastructure Engineering, Vol. 16, 2001.

Search CrossRef
Wu Z., Fujino Y. Special issue: structural health monitoring and intelligent infrastructure. Smart Materials and Structures, Vol. 14, 2006.

Search CrossRef
Chang C. Special issue: management of civil infrastructure. Structure and Infrastructure Engineering, Vol. 3, 2007.

Search CrossRef
Doebling S., Farrar C., Prime M., Shevitz D. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: a Literature Review. Report LA-13070-MS, Los Alamos National Laboratory, Los Alamos, NM, 1996.

Search CrossRef
Sirca G., Adeli H. System identification in structural engineering. Scientia Iranica, Vol. 19, Issue 6, 2012, p. 1355-1364.

Search CrossRef
Ciang C., Lee J.-R., Bang H.-J. Structural health monitoring for a wind turbine system: a review of damage detection methods. Measurement Science and Technology, Vol. 19, Issue 12, 2008, p. 122001.

Search CrossRef
Hameed Z., Hong Y., Cho Y., Ahn S., Song C. Condition monitoring and fault detection of wind turbines and related algorithms: a review. Renewable and Sustainable Energy Reviews, Vol. 13, Issue 1, 2009, p. 1-39.

Search CrossRef
Gross E., Zadoks R., Simmermacher T., Rumsey M. Application of damage detection techniques using wind turbine modal data. 37th Aerospace Sciences Meeting and Exhibit, Reston, Virigina, 1999.

Search CrossRef
Ghoshal A., Sundaresan M., Schulz M., Pai P. Structural health monitoring techniques for wind turbine blades. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 85, Issue 3, 2000, p. 309-324.

Search CrossRef
Adams D., White J., Rumsey M., Farrar C. Structural health monitoring of wind turbines: method and application to a HAWT. Wind Energy, Vol. 14, Issue 4, 2011, p. 603-623.

Search CrossRef
Kraemer P., Fritzen C. Damage identification of structural components of offshore wind energy plants. 9th German Wind Energy Conference, 2008.

Search CrossRef
Swartz R., Lynch J., Sweetman B., Rolfes R., Zerbst S. Structural monitoring of wind turbines using wireless sensor networks. Smart Structures and Systems, Vol. 6, Issue 3, 2010, p. 183-196.

Search CrossRef
Häckell M., Rolfes R. Monitoring a 5MW offshore wind energy converter: Condition parameters and triangulation based extraction of modal parameters. Mechanical Systems and Signal Processing, Vol. 40, Issue 1, 2013, p. 322-343.

Search CrossRef
Koh C., Perry M. Structural Identification and Damage Detection using Genetic Algorithms. Vol. 6. Structures and Infrastructures. CRC Press, 2010.

Search CrossRef
Farrar C., Doebling S. Lessons learned from applications of vibration based damage identification methods to large bridge structure. Proceedings of the International Workshop on Structural Health Monitoring, Vol. 836, 1997, p. 351-370.

Search CrossRef
Jonkman J., Butterfield S., Musial W., Scott G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development. Technical Report February, Los Alamos National Laboratory (LANL), 2009.

Search CrossRef
Jonkman J., Musial W. Offshore Code Comparison Collaboration (OC3) for IEA Task 23 Offshore Wind Technology and Deployment. Technical Report December, National Renewable Energy Laboratory (NREL), 2010.

Search CrossRef
Jonkman J., et al. Offshore Code Comparison Collaboration Continuation (OC4), Phase I Results of Coupled Simulations of an Offshore Wind Turbine with Jacket Support Structure. Technical Report March, National Renewable Energy Laboratory (NREL), 2012.

Search CrossRef
Geem Z., Kim J., Loganathan G. A new heuristic optimization algorithm: harmony search. Simulation, Vol. 76, 2001, p. 60-68.

Search CrossRef
Yang X. Nature-Inspired Metaheuristic Algorithms (1st ed.). Luniver Press, United Kingdom, 2008.

Search CrossRef
Alia O., Mandava R. The variants of the harmony search algorithm: an overview. Artificial Intelligence Review, Vol. 36, Issue 1, 2011, p. 49-68.

Search CrossRef
Hasancebi O., Erdal F., Saka M. An adaptive harmony search method for structural optimization. Journal of Structural Engineering, Vol. 136, 2010, p. 419-431.

Search CrossRef
Jahjouh M., Nackenhorst U. Structural Identification of Two Dimensional Shear Buildings Using a Modified Adaptive Harmony Search Algorithm. Engineering Optimization. CRC Press, 2014, p. 193-198.

Search CrossRef

About this article

Received

Accepted

02 August 2015

Published

09 October 2015

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

harmony search

identification

damage detection

offshore

wind turbine

FAST

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.