Vibration analysis of the beam structure under the moving mass

Han, Huimin; Qiu, Xiumei; Xu, Zongmei; Bai, Runbo

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Vibration analysis of the beam structure under the moving mass

Huimin Han¹

Xiumei Qiu²

Zongmei Xu³

Runbo Bai⁴

^{1, 2, 3, 4}College of Water Conservancy and Civil Engineering, Shandong Agricultural University, Tai’an 271018, China

Corresponding Authors:

Xiumei Qiu, Runbo Bai

Cite the article Download PDF

Downloads 1653

Abstract

Analytical solution of vibration of simply supported beam under the action of centralized moving mass and two numerical methods using life and death element method and displacement contact method are analyzed in this paper. The results show that vertical acceleration resulted from speed and centrifugal acceleration resulted from load moving must be taken into consideration for large quality and high speed. The characteristics and applicable situations of the two numerical methods are also studied to provide a basis for analyzing and considering structural dynamic problems of moving load mass.

1. Introduction

In modern society, it is important to develop national economy and improve people’s living standard by establishing transportation networks. The speed of the train has been constantly improved and the heavy-haul transportation has been developed in more and more countries in recent years. When taking action on the structure (mass of the heavy object cannot be neglected), these heavy moving objects and the structure make up an interactional time-varying vibration system. Therefore, it is of important significance for guarantying the train’s safety and stability to consider the effect of moving object mass on structural vibration [1-3].

Displacement and acceleration are important parameters of structural dynamic response. They can subtly reflect vibration of the structure and can be used to detect structural damage [4, 5]. In this paper, the authors make a comparison between analytical solution of vibration of simply supported beam under the action of centralized moving mass and two numerical analysis methods using ANSYS [6, 7]. The time history curve of displacement response and speed response are given to realize vibration analysis of moving mass. Finally, the authors make a summary of characteristics and applicable situations of each method to provide a basis for analyzing and considering structural dynamic problems of moving load mass.

2. Analytical solution of simply supported beam under moving mass

2.1. Dynamic equilibrium equation and solution

Moving mass acting on the simply supported beam can be simplified into the model shown in Fig. 1. Assuming simply supported beam is a uniform section (Bending moment of inertia is a constant) and wheel mass $M$ moves along beam length but not out of beam body.

Fig. 1Moving mass at a constant speed acting on simply supported beam

Assuming vertical displacement of the mass $y (x, t)$ , acting force on the beam can be represented as:

1

P (x, t) = M g - M \frac{d^{2} y (x, t)}{d t^{2}} .

Based on the assumption of no separation, the following can be deducted:

2

P (x, t) = M g - M (\frac{\partial^{2} y (x, t)}{\partial t^{2}} + 2 v \frac{\partial^{2} y (x, t)}{\partial t^{2}} + v^{2} \frac{\partial^{2} y (x, t)}{\partial x^{2}}) .

In the Eq. (2), physical significance of items in the round bracket is as follows: $\partial^{2} y (x, t) / \partial t^{2}$ represents vertical acceleration of beam vibration where the wheel locates; $2 v \partial^{2} y (x, t) / \partial t^{2}$ represents vertical acceleration resulted from change of vertical speed of the beam due to load moving; $v^{2} \partial^{2} y (x, t) / \partial x^{2}$ represents centrifugal acceleration generated from load moving along the vertical curve due to beam vibration. Therefore, dynamic equilibrium equation of moving mass load is considered as:

3

E I \frac{\partial^{4} y (x, t)}{\partial x^{4}} + ρ A \frac{\partial^{2} y (x, t)}{\partial t^{2}} + c \frac{\partial y (x, t)}{\partial t} = δ (x - v t) P (x, t),

where $E$ is Young’s modulus of the beam material, $I$ is the moment of inertia of the cross-section, $ρ$ is the density of the beam material, $A$ is the cross-sectional area of the beam, $c$ is the beam damping and $δ$ is the Dirac function. Using the modal analysis method, the displacement $y (x, t)$ can be written in the form of generalized coordinates as:

4

y (x, t) = \sum_{i = 1}^{\infty} q_{i} (t) φ_{i} (x),

where $ϕ_{i} (x)$ is the $i$ th order mode of vibration and $q_{i} (t)$ is the generalized coordinates of the mode of vibration. Substitute Eq. (4) into Eq. (3) and calculate the integral to get the following:

5

[ρ A \int_{0}^{L} ϕ_{n}^{2} (x) d x] \frac{d^{2} q_{n} (t)}{d t^{2}} + [c \int_{0}^{L} ϕ_{n}^{2} (x) d x] \frac{d q_{n} (t)}{d t} + [E I \int_{0}^{L} ϕ_{n} (x) \frac{d^{4} ϕ_{n} (x)}{d x^{4}} d x] q_{n} (t)

= M g ϕ_{n} (x) - M \sum_{i = 1}^{\infty} \frac{d^{2} q_{i} (t)}{d t^{2}} ϕ_{i} (x) ϕ_{n} (x) .

Rearrange Eq. (5) and we can get:

6

[(ρ A \int_{0}^{L} ϕ_{n}^{2} (x) d x) {\ddot{q}}_{n} (t) + M \sum_{i = 1}^{\infty} {\ddot{q}}_{i} (t) ϕ_{i} (x) ϕ_{n} (x)] + [2 ξ_{n} ρ A ω_{n} \int_{0}^{L} ϕ_{n}^{2} (x) d x] {\dot{q}}_{n} (t)

+ [E I \int_{0}^{L} ϕ_{n} (x) \frac{d^{4} ϕ_{n} (x)}{d x^{4}} d x] q_{n} (t) = M g ϕ_{n} (x) .

Given that $ϕ_{n} (x)$ has been calculated, Eq. (6) can be deemed as a differential equation for $q_{n} (t)$ $(n = 1, 2, 3...)$ . Use Newmark- $β$ method to calculate $q_{n} (t)$ and the beam response can be obtained.

2.2. Case study

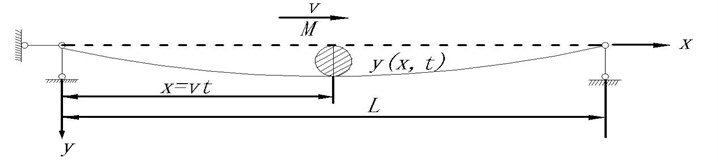
Following the procedure described above, in what follows various cases are created on the basis of a simply supported base beam with dimensions of length 20 m and 45a I-beam as cross-section. The beam mass per unit length and the flexural rigidity EI of the base beam are 80.4 kg/m and 1.43×10^-3 m³, respectively. As examples, masses are selected as 300 kg and 1000 kg, and the moving speeds are 72 km/h and 144 km/h. Time history curve of mid-span displacement and acceleration under the condition of counting and not counting the last two items $(2 v \partial^{2} y (x, t) / \partial t^{2}, v^{2} \partial^{2} y (x, t) / \partial x^{2})$ are shown in Figs. 2 and 3, respectively.

Fig. 2Time history curve of vertical displacement of mid-span under moving mass

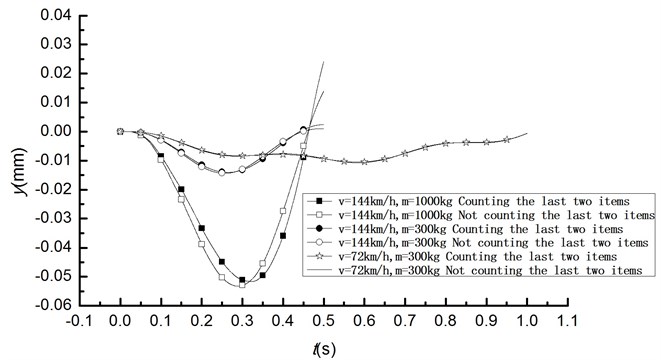
Fig. 3Time history curve of acceleration under moving mass

3. Numerical solution of simply supported beam under moving mass

3.1. Life and death element method

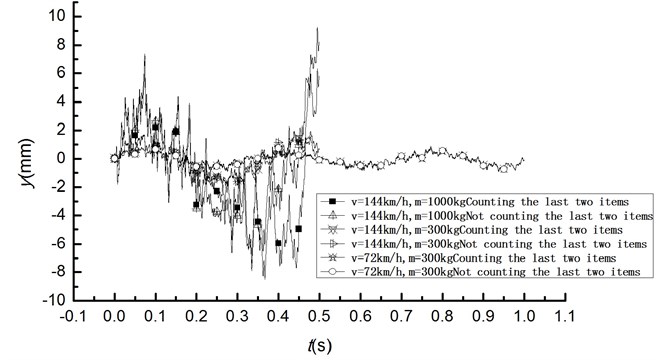
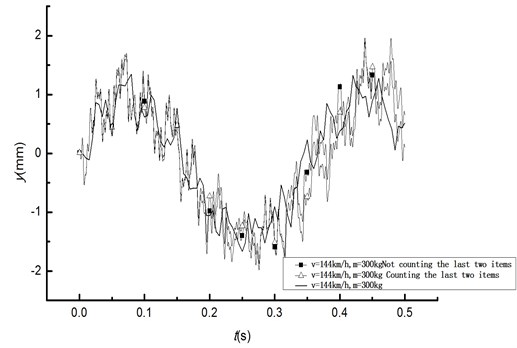
Vibration analysis of the beam model under the action of moving mass with life and death element method is performed in ANSYS using BEAM 189. First, create mass elements on the beam node where moving quality will reach, and kill them all; then as the mass moves to a certain node, activate the mass element at this point and kill the previously activated mass element. Therefore, structural dynamic analysis under the action of moving mass can be realized through such a circulation. Time history curve of displacement and acceleration by applying the moving load $m =$ 300 kg, $v =$ 144 km/h using the life and death element method and the theory analysis resolution are shown in Figs. 4 and 5, respectively.

Fig. 4Time history curve of displacement by life and death element method

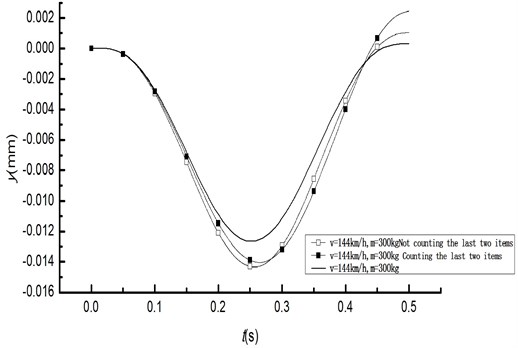
Fig. 5Time history curve of acceleration by life and death element method

3.2. Displacement contact method

Vibration analysis of the beam model under the action of moving mass with displacement contact method is performed in ANSYS using BEAM 189 and MASS 21. First create contact pair between BEAM 189 element and MASS 21 element, and then apply UX displacement on the node of mass element to realize mass moving. Time history curve of displacement and acceleration by applying the moving load $m =$ 300 kg, $v =$ 360 km/h using the displacement contact method and the theory analysis resolution are shown in Figs. 6 and 7, respectively.

4. Conclusions

From dynamic equilibrium equation, it can be seen that the last two items $(2 v \partial^{2} y (x, t) / \partial t^{2}, v^{2} \partial^{2} y (x, t) / \partial x^{2})$ in Eq. (3) is related to bridge mass and moving speed of load. From Figs. 2 and 3, it can be concluded that when the mass is the same, at low speed, it has little impact on the result (displacement) whether the last two items are counting or not, therefore these two items can be ignored for general railway bridge (deformation curvature under the action of live load is small) and existing slow train; when moving mass is large and moves at a high speed, there are great differences with the same tendency whether the last two items are counting or not, therefore the impact of the last two items cannot be ignored for the train at high speed.

Time history curve of beam response by life and death element method and theoretical result not counting the last two items nearly overlap with each other. As node of quality element and bridge node is the same node, moving mass response is basically the same with theoretical solution. However, the method is complicated for multiple moving masses.

Fig. 6Displacement response by displacement contact method

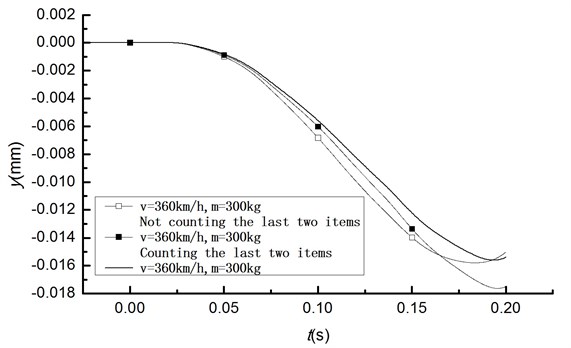
Fig. 7Acceleration response by displacement contact method

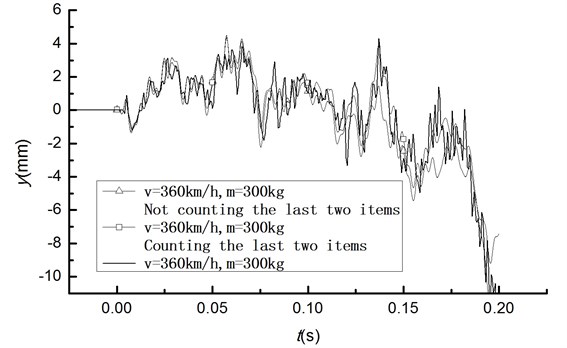
Results of displacement contact method and theoretical results counting the last two items are the same. Compared with life and death element method, it is not necessary to consider whether moving mass moves to the position of beam node for displacement contact method, therefore element length is not limited and only a certain number of elements are required. When the model is complex, for example in the situation with multiple factors such as moving mass, dead-weight of beam and irregularity influence, displacement contact method is superior.

References

Xia He, Zhang Nan Interaction between Vehicle and Structure (2th Edition). Science Press, Beijing, 2005.

Search CrossRef
Cao M. S., Xu H., Bai R. B., Ostachowicz W., Radzieński M., Chen L. Damage characterization in plates using singularity of scale mode shapes. Applied Physics Letters, Vol. 106, 2015, p. 121906.

Search CrossRef
Yu Zhu Study on Bridge Damage Diagnosis based on Structural Response under the action of Moving Load and Wavelet Analysis. Beijing Jiaotong University, Beijing, 2014.

Search CrossRef
Bai R. B., Ostachowicz W., Cao M. S., Su Z. Crack detection in beams in noisy conditions using scale fractal dimension analysis of mode shapes. Smart Materials and Structures, Vol. 23, Issue 6, 2014, p. 065014.

Search CrossRef
Bai R. B., Cao M. S., Su Z., Ostachowicz W., Xu H. Fractal dimension analysis of higher-order mode shapes for damage identification of beam structures. Mathematical Problems in Engineering, Vol. 2012, 2012, p. 454568.

Search CrossRef
Wang Xinmin ANSYS Structural Dynamic Analysis and Application. China Communications Press, Beijing, 2014.

Search CrossRef
Bai R. B., Song X. G., Radzieński M., Cao M. S., Ostachowicz W., Wang S. S. Crack location in beams by data fusion of fractal dimension features of laser-measured operating deflection shapes. Smart Structures and Systems, Vol. 13, Issue 6, 2014, p. 975-991.

Search CrossRef

About this article

Received

Accepted

11 August 2015

Published

18 September 2015

SUBJECTS

Modal analysis

Keywords

moving mass

vibration

beam

analytical solution

numerical solution

Acknowledgements

The authors gratefully acknowledge the Natural Science Foundations of China (No. 51508156), the China Postdoctoral Science Foundation (Grant No. 2014M560386), and the Natural Science Foundation of Shandong Province of China (Grant No. ZR2014EL034).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.