The improved method of coherent sources with double layers

1. Introduction

Wave Superposition Near-field Acoustic Holography uses a radiation sound field generated by the superposition of a series of equivalent sources inside the sound source to replace the radiation sound field of sound source, and it can be used for the reconstruction and prediction of sound source with any shape [1, 2]. It has been widely used since it avoids the complicated computation and singular integral processing of boundary element method, which leads to a high accuracy [3, 4].The sound field separation method with double layers is to separate the target sound source from background noise and obtain the radiation information of target sound source in the acoustic alone [5, 6]. Conventional sound field separation method with double measurement layers separates the sound field based on the mathematical relationship of pressures produced by source and noise on the two measurement layers. Since the mathematical relationship of traditional sound field separation methods including the FFT [7], Statistically Optimal Near-field Acoustic Holography (SONAH) [8, 9]and the equivalent source [10, 11] are all based on holography surface, the separation accuracy is limited by the number of data points on holography surface.

In order to increase the reconstruction accuracy when using less measurement points, an improved sound field separation based on SONAH and equivalent source method is proposed in this paper. Firstly, more data points on two reconstruction surfaces are reconstructed by data on holography surfaces, separately, based on SONAH. The reconstruction surfaces are as close as possible to the holography surface so as to reduce the error and regularization algorithm is also added to reduce the error; Secondly, according to the equivalent source method, the pressures of target sound source on reconstruction surface are separated by use of the pressure transfer relationship between the sound source and two reconstruction surfaces; Finally, the sound field information of target sound source can be reconstructed based on the equivalent source method.

2. Basic theory

2.1. Sound field separation

Sound field separation process is to separate the target sound source from the sound field with background noise. Therefore, it needs two measurement surfaces. According to the relationship of pressures generated by the two sound sources on the two measurement surfaces, the radiation pressure of the target sound source alone can be obtained finally. In order to reduce the number of measurement points and also guarantee a higher calculation accuracy, the sound field information of the two measurement surfaces is extrapolated to each of the reconstruction surface themselves firstly, and then the sound field separation can be realized according to the data points of the two reconstruction surfaces, as shown in Fig. 1.

Fig. 1Sound field separation with two surfaces

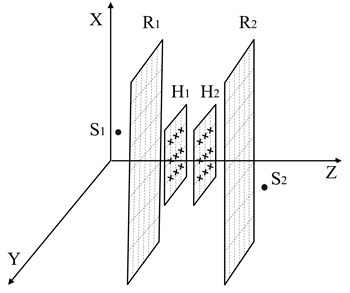
$S_1$, $S_2$, $H_1$, $H_2$, $R_1$ and $R_2$ are the target sound source, background noise, holography 1, holography 2, reconstruction surface 1and reconstruction surface 2. Where $R_1$ and $R_2$ can be obtained by the sound field extrapolation of the data from $H_1$ and $H_2$, respectively. For a steady sound field, the sound pressure of reconstruction surface at any point can be expressed as:

1

$P_{r1}=P_{r11}+P_{r21},$

2

$P_{r2}=P_{r12}+P_{r22},$

where $P_{ri}$ and $P_{rji}$ are the sound pressure of reconstruction surface $i$ and the sound pressure of reconstruction surface $i$ generated by the sound source $j$.

The sound pressure of reconstruction surface can be deduced from the sound pressure of the holography surface obtained by SONAH, as follows:

3

$P_{r1}=P_{h1}{c}_1,$

4

$P_{r2}=P_{h2}{c}_2,$

where $c_1$ and $c_2$ are the weighted coefficient of the holography surface $H_1$ to the reconstruction surface $R_1$ and that of the holography surface $H_2$ to the reconstruction surface $R_2$, respectively.

Putting Eqs. (3) and (4) into Eqs. (1) and (2), respectively, as follows:

5

$P_{h1}{c}_1=P_{r11}+P_{r21},$

6

$P_{h2}{c}_2=p_{r12}+P_{r22}.$

According to the principle of equivalent sources, the sound pressures of different reconstruction surfaces can be expressed as:

7

$P_{r12}=H_{r12}{H}_{r11}^{+}{P}_{r11},$

8

$P_{r21}=H_{r21}{H}_{r22}^{+}{P}_{r22},$

where the $H_{rij}$ is the transfer matrix between point $i$ and $j$, and $H_{rij}^{+}$ is the generalized inverse.

Putting Eqs. (7) and (8) into Eqs. (5) and (6), respectively. As follows:

9

$P_{h1}{c}_1=P_{r11}+H_{r21}{H}_{r22}^{+}{P}_{r22},$

10

$P_{h2}{c}_2=H_{r12}{H}_{r11}^{+}{P}_{r11}+P_{r22}.$

The pressure of reconstruction surface 1 generated by sound source $S_1$ alone can be deduced from the solution of the binary quadratic equations group consist of Eqs. (7) and (8), as follow:

11

$P_{s11}=\frac{P_{h1}{c}_1-H_{r21}{H}_{r22}^{+}{P}_{h2}{c}_2}{I-H_{r21}{H}_{r22}^{+}{H}_{r12}{H}_{r11}^{+}}.$

$P_{r11}$ can be calculated according to the single sound source method that the sound field radiated by sound source $S_1$ alone can be reconstructed and predicted in section 1.2. $P_{r22}$ can also be calculated in the same way to realize the reconstruction and prediction of sound field radiated by $S_2$.

3. Numerical simulation

Two pulse spherical sources $S_1$(–0.15, 0, 0) m and $S_2$(0.15, 0, 0) m with the same radius of 0.01 meter and the same vibration frequency of 1 kHz are set as sound sources. The coordination of holography surface 1 and 2 on axis $z$ are 0.1 m and 0.12 m, respectively. The coordination of $R_1$ and $R_2$ on $z$ axis are 0.009 m and 0.121 m, respectively. The reconstruction surfaces are as close as possible to their holography surfaces themselves so as to reduce the error. The shape of grids with a spacing of 0.07 m is normal on the holography surface and there are 36 measurement points. The number of data points on reconstruction surface with same grid spacing is 81. The SNR is still 30 dB during simulation, the sound pressures of the target sound source on reconstruction surface are as an example.

Fig. 2(a) shows the computational sound pressures of the reconstruction surface 1 radiated by $S_1$ alone after sound field separation; Fig. 2(b) shows the $xoz$ profile of theoretical and computational values of sound source on $R_1$where $L_{err}=$ –29.77 dB. From the Fig. 2, we can see that the reconstruction effect can keep a good accuracy with less measurement points by extrapolating the holography data of the double measurement layers firstly and then predicting. The sound field can be reconstructed and predicted in the same way.

Since the traditional separation method is limited to the measurement points, a comparison about separation effect between the proposed algorithm using 36 measurement points and the traditional method using increasing measurement points gradually is made. Fig. 3 is the error comparison of the two methods, and the measurement points of the traditional method are 7×7, 8×8, 9×9, 10×10 and 11×11, respectively.

Fig. 2Pressure on reconstruction surface: a) pressure of single source; b) theoretical and calculated pressure on xoz profile

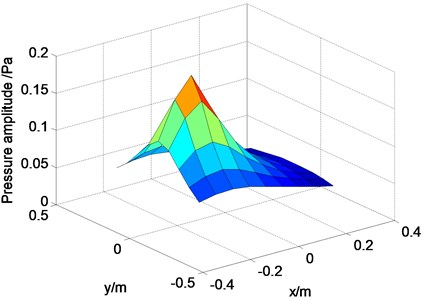
a)

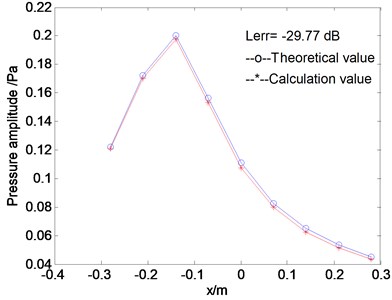
b)

Fig. 3Comparison of errors

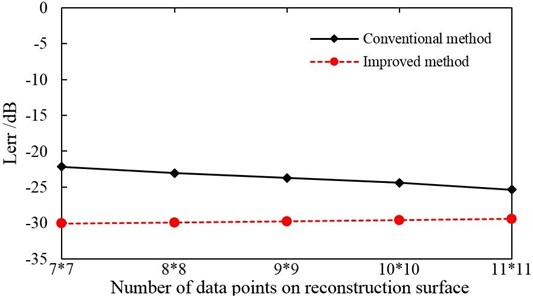
As shown in Fig. 3, the separation error is in reducing as the increasing of the measurement points, which means that the separation accuracy is improved; the separation accuracy of the proposed algorithm has a slight declining along with the increasing of the measurement points, which means that the more of the reconstruction points, the less of the separation error. The proposed algorithm in separation errors are all better than that of the traditional method from the overall view of Fig. 3.

4. Experiment verification

Two loudspeaker boxes were used as sound sources which generated a steady sound field of 1 kHz, and the equipment were set according to the conditions of simulation in section 2. The sensors including three scanning sound pressure sensors and a reference sound pressure sensor (the types are all Brüel & Kjær 4189) are used. The scanning sensors were used to measure the sound pressure at different positions and time and the the reference sensor is fixed. The data of the 36 measurement points can be obtained by dividing the data points of the two measurement surfaces into two groups, and each group made 12 times measurement. The complex sound pressure including amplitude and phase of the measurement surfaces can be calculated from the data measured by the scanning sensors and the reference sensor.

The pressures radiated by sound source alone on reconstruction surface $S_1$ after sound field separation and the contour map of the pressures can be obtained based on the data processing according to the experiment conditions. The number of the data points on the reconstruction surface is 81 and the grid spacing is 0.07 m.

Fig. 4 show the three-dimensional pressure map of the single sound source on the reconstruction surface after sound field separation and the corresponding contour map, respectively. As we can see that the proposed method in this paper could identify the sound source position accurately and separate the target sound source successfully, which means this method could separate the sound field with less measurement points and keep a higher accuracy too.

Fig. 4Reconstruction result: a) the three-dimensional diagram; b) contour map

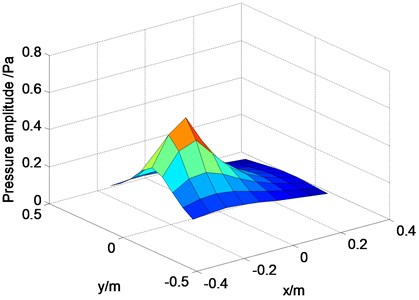
a)

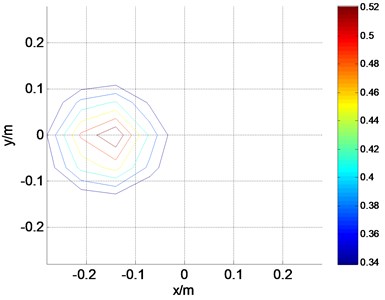
b)

5. Conclusions

In order to reduce the number of measurement points when separating the sound field effectively, an improvement to the traditional equivalent source is made based on the SONAH and the equivalent source method: the data on the two holography surfaces are extrapolated to each of the reconstruction surfaces based on SONAH firstly, and a more accurate data of the reconstruction surfaces can be obtained according to the regularization method which could reduce the error caused by the random noise; and then the data of the reconstruction surface can be obtained by sound field separation based on the equivalent sound source method; finally, the pressures radiated by the target sound source alone after sound field separation can be reconstructed and predicted. The improved method has a higher reconstruction accuracy with less measurement points on the holography surface than the traditional method with more measurement points. The feasibility and effectiveness were verified with experiment further.