Numerical validation of a damage diagnosis method for arch bridges hangers

An, Yonghui; Guan, Delong; Ou, Jinping

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Numerical validation of a damage diagnosis method for arch bridges hangers

Yonghui An¹

Delong Guan²

Jinping Ou³

¹Department of Civil Engineering, State Key Laboratory of Coastal and Offshore Engineering and State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, China

^{2, 3}Department of Civil Engineering, Dalian University of Technology, Dalian, China

Corresponding Author:

Yonghui An

Cite the article Download PDF

Downloads 1273

Abstract

This paper proposes a test method for damage diagnosis of arch bridge hangers. The acceleration response of every hanger under pulse excitation before and after damage is collected and used to extract the damage feature in time domain directly. Then the damage feature waveform before and after damage is obtained respectively by connecting these damage feature values of all measured hangers one by one. Finally the mean value of normalized curvature difference of damage feature waveforms before and after damage is considered as the damage index to diagnose the hangers. The proposed method has a high sensitivity to small damage and the damage sensitivity has no obvious change to hangers with different lengths; moreover, the proposed method doesn’t require the finite element model of the arch bridge. All of these lay a good foundation for damage diagnosis of arch bridge hangers.

1. Introduction

Long-span bridges own significant social and economic value, and there will be a catastrophe after the decline or failure of the bridge bearing capacity [1-2]. To prevent the tragedy and guide the maintenance efficiently, it's necessary to detect tiny damage of the bridge by some feasible methods. The non-destructive test based on vibration information is a good way to diagnose damage quickly and accurately [3].

Vibration-based damage diagnosis methods have been attracting much interest in past decades [4-8]. For the research object of the present work, i.e. arch bridges, many numerical and experimental studies for damage detection have been conducted. For example, Ebert and Lencen [9] diagnosed damage of hangers in a tied arch bridge in Germany using the black-box state space models. Magalhaes et al. [10, 11] introduced a new set of structural health monitoring system based on a hierarchical clustering algorithm which can detect modal parameters automatically and efficiently to diagnose the damage of bridge members and applied it in an arch bridge in Portugal. Zhang and Cheng [12] studied a damage index based on the wavelet transformation, and this damage index can identify both damage location and damage severity of arch structures. Guo et al. [13] used a wavelet packet-based method to detect and locate damage; they analyzed the acceleration responses to identify the damage location and confirm the effectiveness of the method by establishing the two-dimensional and three-dimensional truss finite element (FE) models of the arch bridge. Zhao et al. [14] developed a damage diagnosis method based on the difference of deflection with moving load and verified it successfully based on a steel arch numerical model; they obtained the function of the deflection at the mid span of the arch with the changing positions of the moving load. Li et al. [15] detected the hangers of an arch bridge based on a fast assessment method only with the first and second frequencies, and the accuracy is guaranteed. All these research have obtained a meaningful progress in damage diagnosis and structural health monitoring of arch bridges; however, challenges still exist; for example, the sensitivity of damage detection methods to small damage is still required to be improved.

As the major components between the main bearing structure (the arch) and main traffic structure (the bridge deck), hangers play a vital role in an arch bridge; however, it is easy to be damaged due to corrosion, car strike, scratches, wire breakage, anchor head damage, etc. Early and accurate damage assessment of the hangers is significant for the maintenance and safety of the arch bridge. The main purpose of this paper is to find a model-free method to detect the early damage of hangers. The early work [16] proposed a test method for suspension bridge suspender cables and the method has a high sensitivity to small damage especially for long suspender cables. The present work will make a revision on the basis of this method and then examine its performance in damage diagnosis of arch bridge hangers. The damage sensitivity of the proposed method, and the relationship between the damage sensitivity and the length of hangers, will be shown in this work.

2. The proposed method for damage diagnosis of arch bridge hangers

The early work [16] proposed a damage diagnosis method for suspension bridge suspender cables; this section introduces the damage diagnosis method for arch bridge hangers on the basis of the early method [16]. There is a difference between the present method and the early method, which is shown in Section 2.2.

2.1. Fundamentals of the proposed features

Consider two points on every measured hanger: one is the excitation point, and the other one is the measured point. A pulse excitation is sent to excite every hanger one by one at the excitation point in the transverse direction (i.e. the direction perpendicular to the hangers’ plane), and discrete acceleration data is collected.

Consider a discrete time series $a^{k}$ ( $a_{1}^{k}$ , $a_{2}^{k}$ ,…, $a_{N}^{k}$ ), where $a_{i}^{k} = a^{k} (t_{i})$ is the acceleration signal of the measured point on hanger $k$ at time $t_{i} = i (Δ t)$ , a damage feature $(D F$ ) associated with signal $a^{k}$ is proposed in early work [16] as:

1

D F_{k} = l o g \sum_{i = 1}^{N - 1} {(a_{i}^{k} a_{i + 1}^{k})}^{2},

where $N$ is the number of the points, $Δ t$ is the sampling time interval.

Assuming that the acceleration response at the measured node on hanger $k$ is $a^{k}$ when the excitation amplitude is $F$ , then the acceleration at the measured node on hanger $k$ is $c a^{k}$ when the excitation is $c F$ . Thus, the following equation are given as:

2

D F_{k} (c a^{k}) = D F_{k} + 4 l o g (c) .

As a result, the accelerations should be normalized with respect to the excitation magnitudes prior to beginning calculations of the $D F$ . Response data used in the calculation before and after damage should be the same length. The acceleration data including a complete pulse response is used to compute the $D F$ . After the $D F$ at every node is computed, the waveform of $D F$ (WDF) is created with a linear interpolation between measured nodes.

2.2. Damage diagnosis procedure

Then the “curvature” of WDF is similarly computed as follows:

3

C_{k} = D F_{k - 1} - 2 D F_{k} + D F_{k + 1},

where $C_{k}$ is the curvature at the measured node of hanger $k$ , $D F_{k}$ is the $D F$ value at the measured node of hanger $k$ . The curvature difference value of WDF before and after damage at node $k$ is defined as follows:

4

{(C_{k}^{Δ})}_{r s} = s i g n ((C_{k}^{r})_{i n t a c t} - (C_{k}^{s})_{d a m a g e d}),

where $s i g n$ is –1 and note that it is different with that in damage diagnosis method of suspension bridge suspender cables ( $s i g n$ is +1) [16]; $(C_{k}^{r})_{i n t a c t}$ refers to the curvature at the measured node on hanger $k$ for the $r$ th response record before damage and $(C_{k}^{s})_{d a m a g e d}$ refers to the curvature at the measured node on hanger $k$ for the $s$ th response record after damage.

The damage can be localized as follows:

1) Normalize ${(C_{k}^{Δ})}_{r s}$ for each pair of responses such that the maximum value is 1, i.e.:

5

{(C_{k}^{Δ})}_{r s}^{*} = \frac{{(C_{k}^{Δ})}_{r s}}{\underset{k}{m a x} [{(C_{k}^{Δ})}_{r s}]} .

2) Calculate the mean of the normalized curvature difference for the available response histories, and the damage index ${(D I)}_{k}$ is then defined as:

6

(D I)_{k} = \frac{1}{R S} \sum_{r = 1}^{R} \sum_{s = 1}^{S} {(C_{k}^{Δ})}_{r s}^{*},

where $R$ refers to $R$ pulse response signals that are collected from each hanger of the undamaged structure; $S$ refers to $S$ pulse response signals that are collected from each hanger of the damaged structure. A larger value of $R S$ is better; generally, $R S =$ 20. To avoid having false positive detections, a threshold $δ$ is chosen such that an element is assumed to be damage if the mean normalized difference ${(D I)}_{k}$ is greater than or equal to the threshold $δ$ , i.e.:

7

Damaged hangers = \{(D I)_{k} \geq δ\} .

Setting the threshold $δ$ is discussed in more detail in Section 4.3.

3. Research object

The Ebian Dadu river arch bridge shown in the Fig. 1 is selected to demonstrate the proposed method. The Ebian Dadu river arch bridge was built in 1995, which is located in Sichuan province, China. The arch is built with steel tube filled with concrete. The main span is 138 meters and its ratio of height to span is 1/5. The bridge has 50 hangers.

Fig. 1The research object sketch

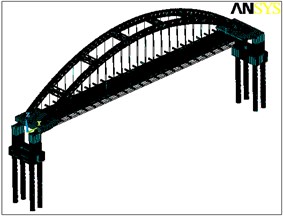
Fig. 2The research object sketch and layout of measured points

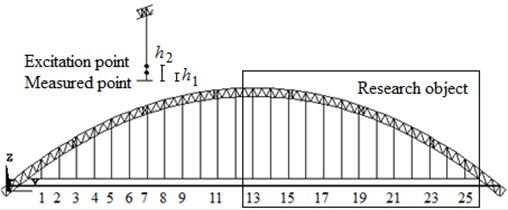
Numerical studies are carried out using ANSYS. The 3-D Elastic Tapered Unsymmetric Beam element (Beam 44) is employed in modeling of arch ribs and cross girder; and the Tension-only Spar element (Link 10) is employed in modeling the hangers. As shown in Fig. 2, the substructure on the right half of the main span is selected as research object. This part of the structure has 13 hangers, and each hanger is divided into many 1 m-in-length elements. To enable the excitation and the installation of the sensor easily, it is recommended that $h_{1}$ and $h_{2}$ be 1 m and 1.5 m respectively (Fig. 2). A pulse excitation is used to excite every hanger at its excitation node in the transverse direction within the FE model. A hanger should be excited on the same node with the same hammer before and after damage. The excitation is recorded by a load cell installed on the hammer, and then the responses can be normalized with respect to excitation magnitude. In simulation, the transverse accelerations of the 13 measured nodes before and after damage are obtained from the undamaged/damaged FE model. The sampling frequency is 50 Hz, and to obtain a complete pulse response, the sampling time is 10 seconds.

4. Numerical validation

In this section, the proposed damage diagnosis method for arch bridge hangers is validated through several numerical damage cases including single and multiple damage cases.

4.1. Influences of ambient excitation and the measurement noise

The pulse responses of hangers are affected by ambient vibration due to traffic, wind, etc. The influence of ambient excitation is simulated by adding additional band-limited white noise excitation (different excitation signals at different nodes) at some nodes on the carriageway (Fig. 3) in transverse and vertical directions, in which the vertical excitation is mainly used to simulate the traffic excitation and the transverse excitation is used to simulate the wind excitation. To verify that the proposed approach is robust enough against the noise, the random noise with 5 % of the measured signal is added to the measurements.

Fig. 3The excitation nodes on the arch bridge deck for ambient excitation

Table 1Numerical damage cases (i#: hanger i)

	Case No.	Description of damage cases
Single damage cases	1	19#: 5 % reduction in the cross-sectional area
Single damage cases	2	25#: 5 % reduction in the cross-sectional area
Multiple damage cases	3 4	18# and 24#: 5 % reduction in the cross-sectional area 14#, 17# and 23#: 5 % reduction in the cross-sectional area

Table 2Excitation magnitudes on every hanger before and after damage

Hanger	13	14	15	16	17	18	19	20	21	22	23	24	25
Undamaged	500	500	400	550	400	600	500	650	550	600	500	400	550
Damaged	550	400	350	500	500	550	450	550	450	500	600	350	650

4.2. Damage cases

The damaged hangers are simulated by reducing its sectional area and increasing its density at the same time to keep its mass identical. As shown in Table 1, six damage cases are implemented to examine the proposed method. Damage cases 1-2 are single damage cases in which hangers 19 and 25 are damaged respectively, which represents a long and a short hanger respectively. Damage case 3 is a two-damage case in which hangers 18 and 24 are damaged. Damage cases 4 is a three-damage case in which hangers 6, 12 and 17 are damaged. Table 2 shows pulse excitation magnitudes for the 20 hangers before and after damage.

4.3. Determining the threshold $δ$

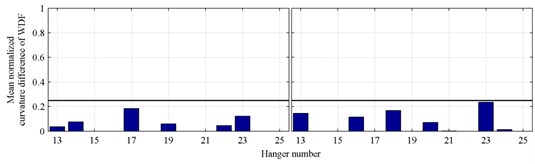
The thresholds $δ$ should be determined based on results of undamaged cases of a given arch bridge. To avoid false positive elements, $δ$ is defined as a value greater than the mean normalized curvature difference ${(D I)}_{k}$ of the undamaged cases. In which ${(D I)}_{k}$ is calculated based on different acceleration signals from the undamaged structure. Fig. 4 shows two ${(D I)}_{k}$ results of the undamaged case based on 20 identifications, in which $δ$ is determined to be 0.25 to avoid the false positive results.

Fig. 4DIk results of undamaged cases

4.4. Damage diagnosis results

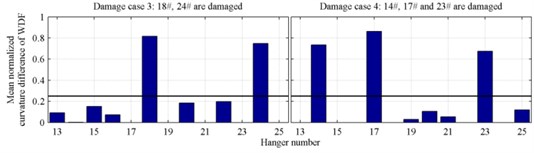
Damage cases 1-4 are identified using the proposed method based on 20 identifications. Damage diagnosis results of single damage cases 1-2 are shown in Fig. 5, and diagnosis results of multiple damage cases 3-4 are shown in Fig. 6; in which 5 % stiffness reduction of hangers with different length can be identified accurately in both single and multiple damage cases.

Fig. 5Damage localization results of single damage cases with 5 % noise level

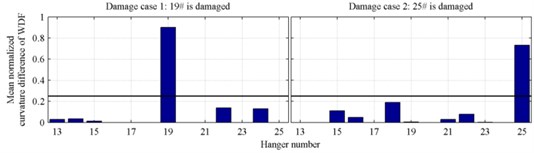
Fig. 6Damage localization results of multiple damage cases with 5 % noise level

5. Conclusions

This paper proposes a test method for damage diagnosis of arch bridge hangers. Simulation results of both single and multiple damage cases indicate the proposed method can be used to identify the damaged hangers well. The conclusions are summarized as follows:

1) The proposed method has high damage sensitivity to small damage of arch bridge hangers: it can be used to diagnose 5 % reduction in the cross-sectional area of all hangers.

2) For the damage diagnosis method of suspension bridge suspender cables in early work [16], damage sensitivity is in inverse proportion to the length of a suspender cable; compared with the early method, the present method does not show different damage sensitivity to arch bridges hangers with different lengths.

3) With the responses of the undamaged and damaged hangers, the present method doesn’t require the FE model of an arch bridge; it avoids the workload of model development and updating.

References

Cruz P. J. S., Salgado R. Performance of vibration-based damage detection methods in bridges. Computer-Aided Civil and Infrastructure Engineering, Vol. 24, Issue 1, 2009, p. 62-79.

Search CrossRef
Jafarkhani R., Masri S. F. Finite element modal updating using evolutionary strategy for damage detection. Computer-Aided Civil and Infrastructure Engineering, Vol. 26, Issue 3, 2011, p. 207-224.

Search CrossRef
Cerri M. N., Ruta G. C. Detection of localised damage in plane circular arches by frequency data. Journal of Sound and Vibration, Vol. 270, Issues 1-2, 2004, p. 39-59.

Search CrossRef
Sohn H., Farrar C. R., Hemez F. M., Czarnecki J. J. A Review of Structural Health Monitoring Literature: 1996-2001. Los Alamos National Laboratory Report, 2004.

Search CrossRef
Cao M. S., Ostachowicz W., Bai R. B., Radzieński M. Fractal mechanism for characterizing singularity of mode shape for damage detection. Applied Physics Letters, Vol. 103, Issue 22, 2013, p. 221906.

Search CrossRef
Cao M. S., Ostachowicz W., Radzieński M., Xu W. Multiscale shear-strain gradient for detecting delamination in composite laminates. Applied Physics Letters, Vol. 103, Issue 10, 2013, p. 101910.

Search CrossRef
An Y. H., Ou J. P., Li J., Spencer B. F. Stochastic DLV method for steel truss structures: simulation and experiment. Smart Structures and Systems, Vol. 14, Issue 2, 2013, p. 105-128.

Search CrossRef
An Y. H., Błachowski B., Ou J. P. A degree of dispersion-based damage localization method. Structural Control and Health Monitoring, 2015.

Search CrossRef
Ebert C., Lencen A. Experiments for damage detection by subspace identification on a tied arch bridge. Proceedings of the Fifth International IABMAS Conference on Bridge Maintenance, Safety, Management and Life-Cycle Optimization, Philadelphia, USA, 2010, p. 1632-1638.

Search CrossRef
Magalhaes F., Cunha A., Caetano E. Online automatic identification of the modal parameters of a long span arch bridge. Mechanical Systems and Signal Processing, Vol. 23, Issue 2, 2009, p. 316-329.

Search CrossRef
Magalhaes F., Cunha A., Caetano E. Vibration based structural health monitoring of an arch bridge: from automated OMA to damage detection. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 212-228.

Search CrossRef
Zhang J., Cheng L. Y. Investigation of combination characteristic of damage location and intensity in arch using wavelet coefficient. Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 2011, p. 370-373.

Search CrossRef
Guo H. Y., Lin J. R., Li Z. L. Structural damage localization of steel arch bridge based on wavelet packet transform. Software Engineering and Knowledge Engineering: Theory and Practice, Vol. 114, 2012, p. 53-62.

Search CrossRef
Zhao Z., Nie Z. H., Ma H. W. Damage identification of the arch bridge based on the difference of deflection with moving load. Applied Mechanics and Materials, Vol. 578, 2014, p. 1096-1100.

Search CrossRef
Li X. S., Sun M., Fu C. C. Fast Assessment Method of Arch-Girder Composite Bridges. Bridge Maintenance, Safety, Management and Life Extension, Shanghai, China, 2014, p. 1527-1534.

Search CrossRef
An Y. H., Spencer B. F., Ou J. P. A test method for damage diagnosis of suspension bridge suspender cables. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 10, 2015, p. 771-784.

Search CrossRef

About this article

Received

Accepted

31 August 2015

Published

18 September 2015

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

damage diagnosis method

hangers

arch bridge

damage sensitivity

model free

Acknowledgements

The authors are grateful for the financial support from the National Key Basic Research Program of China (2015CB060000, 2011CB013705), the National Natural Science Foundation of China (51508070), the China Postdoctoral Science Foundation (2014M560208, 2015T80252), the Fundamental Research Funds for the Central Universities of China (DUT14RC(3)051).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.