The stability of the tethered trailer and its control

Ma, Hongchao; Chen, Ning; Tai, Yongpeng

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

The stability of the tethered trailer and its control

Hongchao Ma¹

Ning Chen²

Yongpeng Tai³

^{1, 2}College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China

³College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037, China

Corresponding Author:

Ning Chen

Cite the article Download PDF

Downloads 1394

Abstract

Tethered trailer vehicle is a nonprofessional tractor that drags an unpowered vehicle with rope. In this paper, a nonlinear dynamic model of the tractor is developed. With the Dugoff’s tire model. A new nonlinear tethered tractor-trailer model is created to simulate critical parameters. A trailer front-wheel steering feedback control strategy is derived in order to improve stability and trajectory tracking feature the comparison of the simulation results for tension of the traction rope, the trajectory following resistance, and the handling stability clearly demonstrates the efficacy of the proposed control strategy.

1. Introduction

Tethered trailer vehicle is a non-professional tractor that drags an unpowered vehicle with rope. This system has many hazardous problems, such as poor operating stability, and fragile connection between the tractor and trailer. High concentration and rational cooperation is needed for the tethered tractor-trailer combination to moving normally. The drivers both in tractor unit and trailer unit must make a correct judgment and give a timely response for the cases of cornering, accelerating, up and down hill and breaking maneuvers. However, the vehicle is not safe and has lower stability when it comes across some emergency conditions.

For the past decades, the handling stability of tractor-trailer vehicles have achieved great progress. David Cebon, et al. [1] give a braking-based stability control system of the towing vehicle at high speed, the control system and the steering system improved the yaw stability of the combination.

Huang, et al. [2] presents a math model for tractor-semitrailer combination based on reasonable theoretical hypotheses, and the model can well predict the behavior of the vehicle under various dangerous conditions. Erlcan Kayacan, et al. [3] studied an autonomous tractor-trailer system. He proposed a complete nonlinear dynamic model for the tractor-trailer system. All in all, a nonlinear dynamic vehicle is needed to accurately describe the actual condition.

Vehicle-following systems are one of the most important parts of advanced driver assistance. For tethered trailer vehicles, it is important for follower vehicle to keep in compliance with the trajectory of the tractor vehicle [4]. Steven A. Velinsky, et al. [5] studied a novel type of snowplow that consists of a conventional snowplow vehicle and a steerable, plow-mounted trailer. An active steering control for the trailer axle is presented and is proved to be effective in trajectory tracking.

For the tethered trailer vehicle until now, little attention has been paid to it, and there are relatively few works on relevant discipline. This makes such a study essential.

2. Vehicle dynamic model and simulation

The tractor model is a seven-degree-of-freedom vehicle model, which includes lateral, longitudinal and yaw motions, and rotation dynamics of the wheels. In this paper, we assume that the tires present the same mechanical characteristics, and the front wheels have equivalent steering angle and constitute a reasonable ratio with the steering wheel angle. For simplicity, the damping of transmission system is ignored, the power train only play a role of transmitting torque, and the torsion and shimmy are also not taken into consideration.

Fig. 1Scheme of tractor and forces

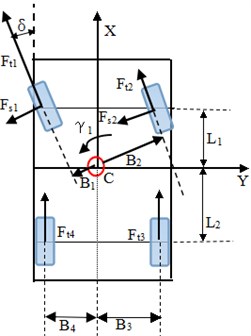
As shown in Fig. 1, dynamic equations of X-axis and Y-axis motions for the tractor units in the fixed vehicle coordinate are given by:

1

m ({\dot{v}}_{x} - v_{y} \cdot r) = F_{t 1} \cdot c o s δ - F_{s 1} \cdot s i n δ + F_{t 2} \cdot c o s δ - F_{s 2} \cdot s i n δ + F_{t 3} + F_{t 4},

2

m ({\dot{v}}_{y} + v_{x} \cdot r) = F_{s 1} \cdot c o s δ + F_{t 1} \cdot s i n δ + F_{s 2} \cdot c o s δ + F_{t 2} \cdot s i n δ + F_{s 3} + F_{s 4},

$v_{x}$ and $v_{y}$ represent the vehicle longitudinal and lateral velocity, respectively. The front-left wheel, front-right wheel, rear-right wheel and rear-left wheel are subscript as 1, 2, 3 and 4, respectively. $F_{t i}$ and $F_{s i}$ stand for the longitudinal and lateral force. For the yaw motion equations, it can be expressed as:

3

I_{z} \cdot \dot{γ} = B_{1} (F_{s 1} \cdot s i n δ - F_{t 1} \cdot c o s δ) + B_{2} (F_{s 2} \cdot s i n δ + F_{t 2} \cdot c o s δ) + B_{3} F_{t 3}

- B_{4} F_{t 4} + L_{1} (F_{t 1} \cdot s i n δ + F_{s 1} \cdot c o s δ + F_{t 2} \cdot s i n δ + F_{s 2} \cdot c o s δ) - L_{2} (F_{s 3} + F_{s 4}),

$B_{i}$ denotes the vertical distance from CG to each tire. $δ$ is a very small value, in this paper, we obtain a reduced equation $B_{1} = B_{2} = B_{3} = B_{4}$ for vehicle dynamic. $L_{1}$ and $L_{2}$ represent the distance from CG to front and rear axle respectively.

2.1. Tire model

The tire accepts vertical load and adhesion force generated by the friction on the road surface. The torque outputs, which are transformed from the engine into traction power, also need friction between tire and road. Dugoff tire model assumes a rectangular contact region between tire and road surface. According to the state of motion and elastic deformation of the contact region, longitudinal slip rate and variation amount of sideslip angle could be calculated. Then take into account the sideslip angle $α$ , longitudinal slip rate $i_{s}$ and the vertical load of tire $F_{z}$ , the longitudinal force $F_{t}$ and lateral force of tire $F_{s}$ can also be known.

4

F_{t} = \frac{C_{i} \cdot i_{s}}{1 - i_{s}} \cdot f (s),

5

F_{s} = \frac{C_{α} \cdot t a n α}{1 - i_{s}} \cdot f (s),

6

f (s) = \{\begin{array}{l} 2 (1 - s), & s < 1, \\ 1, & s \geq 1, \end{array}

7

s = \frac{μ F_{z i} (1 - i_{s})}{2 \sqrt{{c_{i}}^{2} \cdot {i_{s}}^{2} + {c_{α}}^{2} \cdot {t a n}^{2} α}},

where $C_{i}$ is the tire cornering stiffness, $C_{α}$ is the tire longitudinal stiffness, $s$ is the vehicle dynamic parameter.The vehicle parameters are shown in Table 1.

Table 1Vehicle parameters

Distance from CG to each wheel $B_{1}$ , $B_{2}$ , $B_{3}$ , $B_{4}$	0.9 m
Distance from CG to front/rear axle $L_{1}$ , $L_{2}$	1.2 m,1.3 m
Tractor/trailer mass	1500 kg
Tractor/trailer moment of inertia $I_{z}$	3000 kg·m²
Distance from front hitch point to rear axle of the tractor $h_{1}$	0.8 m
Distance from rear hitch point to rear axle of the tractor $h_{2}$	0.7 m
Longitudinal stiffness of tire $c_{i}$	50 kn/rad
Lateral stiffness of tire $c_{α}$	30 kn/rad
Tire radius	0.3 m
The vertical load of front wheel $F_{z 1}$ , $F_{z 2}$	3825.9 n
The vertical load of rear wheel $F_{z 3}$ , $F_{z 4}$	3535.6 n
Tractor/trailer CG height $H$	0.5 m

2.2. Dynamic simulation

Generally, the trailer unit is unpowered and the steering mechanical runs normally, which is the main issue in this paper. The tension between tractor unit and trailer can be expressed as:

8

T = \{\begin{array}{l} k_{1} Δ + k_{2} Δ^{3}, & Δ \geq 0, \\ 0, & Δ < 0, \end{array}

where $Δ$ is the elongation of traction rope, and $k_{1}$ and $k_{2}$ denote the stiffness parameter of rope which means that the tension is identified as nonlinear. From the former equation, the simulation model can be created and the vehicle parameters are the same for simplification. For the first step, the length of rope is the variable that analyze the tension of traction rope, the trajectory of the tractor unit and the trailer unit, the change of sideslip angle and yaw rate. During the simulation process, the rope length, as a critical parameter, is selected to be 3 m and 5 m with the consideration of actual condition. The front steering wheel $δ$ is changed as 0.02 rad with the purpose of getting a stable vehicle state.

The comparison of Figs. 2 and 3 shows that when the rope length is 3 meters, although the starting state performs two small amplitude vibrations, the tractor and trailer exhibit a stable state (in Figs. 2 and 3: a) trajectory of the tractor- trailer; b) tension of the traction rope; c) sideslip angle of the tractor and trailer; d) yaw rate of the tractor and trailer). When the rope length increases to 5 meters, the trajectory differences of two units maintain enlarge. In addition, the tension of rope grows greatly, the sideslip angle unfolds the identical tendency, but the yaw rate performs the same value under stable state ultimately; the most important is that the vibration period becomes longer with the fact that the frequency and amplitude get very complicated. From the above analysis, the results can be summarized that the rope length have a very large effect on the handling stability of trailer unit, the increase of rope length would cause the trajectory following resistance decreased.

3. Control strategy

The simulation results of the previous section show that during the turning process, if the front wheel of trailer unit cannot active steer, the mutual interference force between the tractor and trailer would cause the handling stability deteriorate. How does the trailer unit achieve active steering? Option one is that the front wheel of trailer can steer automatically.

Fig. 2Vehicle response curve with the rope length is 3 m

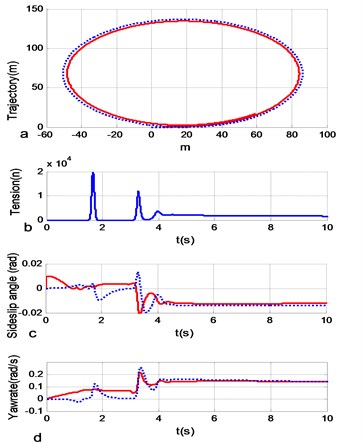
Fig. 3Vehicle response curve with the rope length is 5 m

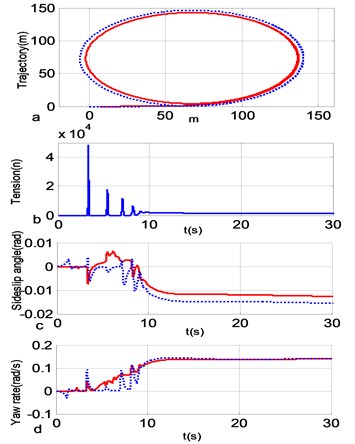
Fig. 4Tethered tractor-trailer model

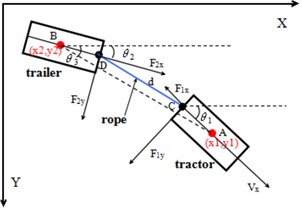
Automatic steering control strategy is based on feedback control principle of modern control theory. The bidirectional force sensor installed on articulated point of the trailer can obtain the direct deviation angle between the direction of traction rope tension and the tractor’s driving direction. When the steering wheel of tractor has a constant angle, the whole process continuously regulates the turning angle of trailer according to the changes of vehicle movement and its path. As Fig. 4 shows, the mathematical model for the direct deviation angle calculation of the equation, which can be expressed as:

9

δ_{f} (t) = K_{m} Δ ϕ (t - T_{s}),

10

δ_{f} (s) = \frac{K_{m} Δ ϕ}{e^{T_{s} s}},

where $T_{s}$ is the delay time of mechanism and $K_{m}$ stands for gaining coefficient. $Δ ϕ$ represents the direct deviation angle. To simplify the calculation, Eq. (10) is the Laplace transform of Eq. (9). To expand the $e^{T s s}$ as Taylor series and only anterior two terms are reserved because the $T_{s}$ is small.

11

(1 + T_{s} s) δ_{f} (s) = K_{m} Δ ϕ,

12

{\dot{δ}}_{f} (t) = - \frac{1}{T_{s}} δ_{f} (t) + \frac{1}{T_{s}} K_{m} Δ ϕ .

Eq. (12) is the inverse Laplace transform of Eq. (11).

3.1. Simulation

The tractor unit and trailer unit transferred to unsafe state soon when the traction rope increased to 5 meters. The simulation parameters with feedback control are selected to be the same as the former for comparison.

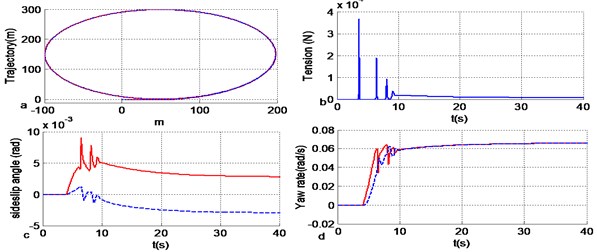
The trajectory following resistance has a significant improvement with feedback control as shown in Fig. 5. The trajectory difference trends to be zero, which proves that the control strategy is effective. The traction tension does not decrease very much, and the yaw rate also performs to be similar. The vibration has a commendable progress, and the setting of time delay diminishes the vibration between the tractor and the trailer.

Fig. 5Vehicle response curve based on driver model control with the rope length is 5 meters

4. Conclusions

In this paper, a seven-degree-of-freedom vehicle model and a new nonlinear tethered tractor-trailer combination model are presented to describe the actual condition of rope tow. The model considers the nonlinear traction rope, and utilizes a modified Dugoff’s tire friction model. The comparison of different rope length demonstrates that the dynamics model can accurately predict that the increasing of rope length leads to a worse trajectory following resistance. In addition, the driver model control with automatic steering control strategy is developed to improve the handling stability of the tractor and trailer system. The simulation results demonstrate that the feedback control from the trailer unit could improve the trajectory following resistant significantly.

References

Roebuck R., et al. Implementation of trailer steering control on a multi-unit vehicle at high speeds. Journal of Dynamic Systems Measurement and Control-Transactions of the ASME, Vol. 136, Issue 2, 2014.

Search CrossRef
Huang Chaosheng, Kui Hailin, Wu Zhenxin A simulation study on the dynamics of tractor-semitrailer combination. Automotive Engineering, Vol. 6, 2005, p. 744-750.

Search CrossRef
Kayacan E., et al. Nonlinear modeling and identification of an autonomous tractor-trailer system. Computers and Electronics in Agriculture, Vol. 106, 2014, p. 1-10.

Search CrossRef
Chen W. H., et al. A partially flexible virtual trailer link model for vehicle-following systems. Transactions of the Institute of Measurement and Control, Vol. 37, Issue 2, 2015, p. 273-281.

Search CrossRef
Jae Young Kang, et al. Nonlinear vehicle dynamics and trailer steering control of tow plow, a steerable articulated snow plowing vehicle system. Journal of Dynamic Systems, Measurement, and Control, Vol. 137, Issue 1, 2015.

Search CrossRef

About this article

Received

Accepted

31 August 2015

Published

18 September 2015

SUBJECTS

Vibration in transportation engineering

Keywords

nonlinear vehicle model

rope-dragged tractor

feedback control

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11272159).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.