Filtering procedure for local damage detection in gearbox using alpha stable modeling

1. Introduction

Local damage detection in heavy-duty mechanical systems is currently one of the most explored and investigated field of the modern condition monitoring [1, 2]. Some of the methods in this field are based on the analysis of the signal in the time domain [3-8]. Most of them use impulsive character of the signal [9-11] or specific structure of envelope spectrum [12]. One of the approach exploits cyclostationarity behaviour of the vibration signal [13-15]. However, signal from machine with local damage is very non-stationary and have complex structure therefore here is need to apply more advanced techniques and analyse the signal in time-frequency domain [16-25].

In the literature for many proposed methods of local damage detection first the signal is decomposed [2-3] and then the further analysis is provided in order to extract its informative part. Most of the methods are based on the specific behaviour of the decomposed signal, like impulsiveness or its cyclic (or periodic) character observable especially in the sub-signals corresponding to the frequency bands of underlying signal after division of its frequency spectrum. In that cases the measures of impulsiveness (or periodicity) are applied to appropriate sub-signals and then the informative frequency bands are selected [10, 12, 26-28]. We only mention here methods based on the local maxima [29], sparsity [30-32] or statistical measures based on moments, quantiles, or cumulative distribution functions [28] and stochastic modelling techniques [33-39].

In this paper we propose a method of local damage detection that is based on the enhancement of noisy vibration signal. In the developed technique we use the α-stable distribution approach [37]. More precisely, we estimate the stability index for each sub-signal from time-frequency representation taking the assumption that it can be modelled by using α-stable distribution which is an extension of the classical Gaussian one [40]. In our approach we obtain distribution of the stability index versus frequency, that provides similar picture as spectral kurtosis well known in the literature. On the basis of the obtained characteristic we can design the filter in order to enhance of the raw signal. To evaluate efficiency of our method we compare raw filtered signal. This comparison we present in time, time-frequency and frequency (envelope spectrum) domains. The presented methodology we apply to real vibration signal from two stage heavy duty gearbox used in mining industry.

The paper is organized as follows. In Section 2 we present in details methodology related to $\alpha$-stable distribution modelling and procedure of filter design based on this approach. In Section 3 we analyse the real vibration signal in the context of the presented methodology. The last section contains conclusions.

2. Theoretical background

In this section we present the procedure of extraction of informative part of vibration signal. We provide here necessary definitions related to applied statistical methods and introduce novel technique that allows us to enhance informative frequency band in order to detect the local damage. We extend the classical methodology based on the spectral kurtosis [11] and propose to model the sub-signals corresponding to frequency bands in time-frequency representation (spectrogram) by using $\alpha$-stable (stable) distribution. This distribution is very often treated as a natural extension of the classical Gaussian one. Moreover it is worth mentioning, the stable distribution is especially important in the context of modelling of data with visible jumps however for specific values of stable distribution parameters it reduces to Gaussian one. As a result of sub-signals modelling, we obtain distribution of stability index with respect to frequencies. Such characteristic is basis for filter design used for raw signal enhancement.

In the first step of the introduced method the raw signal is transformed into the time-frequency map through the short-time Fourier transform (STFT) [41]:

where $w\left(t-\tau \right)$ is the shifted window and $x_k$ is the input signal. Each sub-signal corresponding to appropriate frequencies can be treated as a time series. Since the STFT matrix is complex, absolute value needs to be taken in order to obtain the spectrogram. In the proposed procedure we assume the sub-signals corresponding to appropriate frequencies from the spectrogram constitute samples from $\alpha$-stable distribution. This is related to the fact that for sub-signals with impulsive behavior the stability parameter $\alpha$ tends to be lower than for sub-signals without impulses and hence the parameter can be treated as a selector for informative frequency band selection. We mention, a random variable $X$ is an $\alpha$-stable distributed if its characteristic function takes the following form [42]:

where $\alpha$$(0<\alpha \le 2)$ is stability parameter, $\beta$$(-1\le \beta \le 1)$ is asymmetry parameter, $\sigma$$(\sigma >0)$ is scale parameter and $\mu$$(\mu \in R)$ is location parameter. In our procedure by the assumption that the sub-signals are described by the $\alpha$-stable distribution, in the next step for each time series corresponding to appropriate frequencies we estimate the $\alpha$ parameter [43]. In this paper we apply the regression method which is based on the characteristic function of the considered distribution (see Eq. (2)). After modelling of appropriate sub-signals by using stable distribution we obtain a set of $\alpha$ parameters corresponding to frequencies. The next step of the procedure is to design the filter. The filter ($\alpha$-filter) is defined as follows:

where $\alpha \left(f\right)$ is the estimated $\alpha$ parameter for sub-signal corresponding to frequency $f$. At the end the signal is filtered and its main characteristics are analyzed.

3. Real data analysis

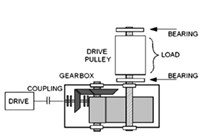
To prove efficiency of the proposed method we apply it to the real vibration signal from complex machine operating in the harsh environment in mining industry. Measurements have been performed using Bruel-Kjaer Pulse system with parameters of data acquisition as follows: length of the signal 2.5 s, sampling frequency equal to 8192 Hz and expected fault frequency equal to 4.1 Hz. The signals were acquired using an accelerometer located on the bearing’s housing in horizontal direction. The machine was normally loaded and the rotational speed was approximately constant during the data acquisition (Fig. 1).

Fig. 1a) – Scheme of the investigated machinery, b) – sensor location in gearbox case, c) – coupling between gearbox and pulley, d) – sensor location in pulley case

a)

b)

c)

d)

Fig. 2Waveform of acquired signal (top panel) with its envelope spectra (bottom panel)

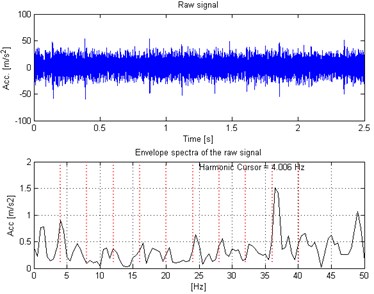
Fig. 3Spectrogram of the acquired signal

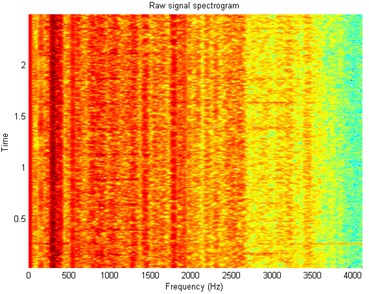
Fig. 4Filter characteristic based on the spectrogram frequency sub-signals

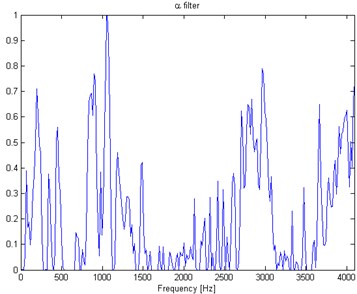
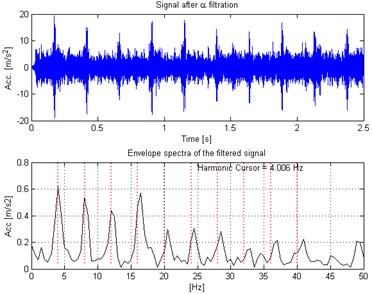
In Fig. 2 top panel the acquired vibration signal from the two-stage gearbox is presented in time domain. One can notice some impulses, but it cannot be concluded that they come from the damage. Furthermore, in the Fig. 2 bottom panel we present the envelope spectra of the signal. After performing visual inspection of the examined gearbox, it was found that damage is localized on the tooth in gear-wheel mounted on second (middle) shaft in the gearbox. Damage frequency is calculated with the machine kinematics and localized at 4.1 Hz. As one can see, it is hard to find harmonics of the fundamental frequency at envelope spectra of raw signal. This is the main reason to apply methodology for the enhancement of the impulses related to the fault. In Fig. 3 spectrogram of the raw signal is presented. We cannot easily select the informative frequency band. In Fig. 4, there is presented the $\alpha$-filter characteristics. While in Fig. 5 we show a time-frequency map of the signal after performing $\alpha$ filtration. One can easily notice significant increase in energy for the impulses related to the fault. Furthermore, Fig. 6 contains the filtered signal (top panel) in time domain and envelope spectra (bottom panel). It can be denoted that the damage can be observable in time domain (visible cyclic impulses) as well as in envelope spectra. The fundamental frequency with transparent location of its harmonics we observe in both panels of Fig. 6.

Fig. 5Spectrogram of the α-filtered signal

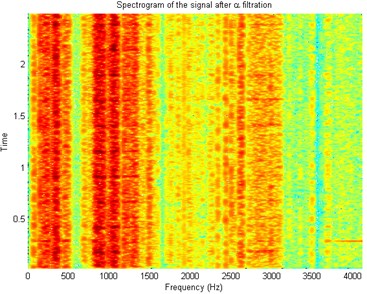
Fig. 6Waveform of the α-filtered signal (top panel) with its envelope spectra (bottom panel)

4. Conclusions

In the paper a novel method for filtering vibration signals is proposed. The filtering procedure was developed in order to enhance the raw vibration signal, i.e. improve its signal to noise ratio.

The approach is based on the fundamental property, meaning impulsivity in a certain frequency band indicating presence of the fault in the machine. The key problem is to identify these frequency band and create appropriate filter characteristic. For purpose of measuring impulsivity we adapted $\alpha$-stable distribution and its stability parameter $\alpha$. In the literature the $\alpha$-stable distribution is especially important in modeling of processes with impulsive character.

In the case of machine in the healthy condition, distribution of signal (and consequently each sub-signal for given frequency band) is close to the Gaussian which is particular case of the $\alpha$-stable distribution with parameter $\alpha$ close to 2. For machines in the bad condition, impulsivity in the signal will affect many frequency bands (energy flow in that bands will reveal impulsive character, too). In consequence, stability parameter will become significantly smaller than 2.

Distribution of alpha parameter vs. frequency allows to indicate so called informative frequency band and might be used as filter characteristic. Application of the method for real vibration signals proved that both in time domain as well as in envelope spectrum signal reveals much clearly presence of damage. After filtering, in time domain cyclic impulses are more visible. Also in envelope spectrum one might notice fundamental frequency together with family of harmonics that is clear signature of local damage in gearbox.