Modernization of high-frequency vibratory table with an electromagnetic drive: theoretical principle and modeling

Gursky, Volodymyr; Lanets, Oleksiy

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 30 December 2015

Check for updates

Modernization of high-frequency vibratory table with an electromagnetic drive: theoretical principle and modeling

Volodymyr Gursky¹

Oleksiy Lanets²

^{1, 2}Lviv Polytechnic National University, Department of Mechanics and Automation Engineering (MAE), Institute of Engineering Mechanics and Transport, 12 Bandera str., Lviv, 79013, Ukraine

Corresponding Author:

Volodymyr Gursky

Cite the article Download PDF

Downloads 1231

Abstract

The task of modernization of high-frequency harmonically resonance vibratory table with an electromagnetic drive is considered. An idea of modernization consists in the increase of technological possibilities by realization of two-frequency resonance office by a change of stiffness and inertia parameters of the two-mass machine. The initial of two-mass system is translated in three-mass, which has two eigenfrequencies of vibrations, which are determined by resiliently and inertial parameters of the system. The formula to calculation of stiffness parameter of the additional module is got, based on a task of synthesis of multipleness of eigenfrequencies of the three-mass oscillating system and provide of the two-frequency resonance mode. Inertia of oscillating mass on descriptions of acceleration of working mass (maximal value and betweenness by his harmonics value) the influence is studied. Models for description of vibrations in the probed oscillation systems, which take into account the chart of feed of electromagnetic vibroexciters, structure of the system, its parameters and influence of load on the mass-damping descriptions of working mass are offered.

1. Introduction

The resonance systems have the practical use in technological processes, and proper them ponderable advantages have linear models. Among them simplicity of structural realization and exactness of calculation, which it doesn’t follow to cast aside from point of subsequent improvements of such machines type. However, from of the technological expedience point one-frequency systems ineffective. They are prevailed by poly-frequency systems – in particular by harmonically and vibro-impact. It predetermines the necessity of the use of the existent one-frequency systems for their subsequent translation in more technologically efficiency. A modernization of wide public of harmonically machines with an electromagnetic drive is a fully requiring measure for expansion of technological quality of work this machines class.

2. Problem statement

Structurally self-reactance transformation is basis of modernization of oscillation machines. Thus absence of integral methods which light up theoretical calculation principles and concrete practical facilities is the issue of the day, as limits appearance of new, more technologically and energy efficiency machines.

3. Analysis of modern information sources on the subject of the article

The resonance oscillation systems are able effectively to work at the certain stiffness-inertial parameters of the system, and that is why technological changes substantially influence on firmness of their kinematics parameters [1-4]. Therefore, indemnification of influence of technological factors is provided by the change of the dynamic modes due to influence of parameters of indignation on the amplitude-frequency characteristic of the oscillating system. This is provided of control system of a drive [2], and that entailed appearance of adaptive machines. However, the prime price of adaptive facilities is not fully grounded of technical feasibilities of harmonious machines. It is expedient to carry out the improvement of harmonious the two-mass resonance machines by two directions – is an improvement of technological and functioning power efficiency. The first direction is provided by expansion of harmonious composition of vibrations of working mass by realization of the by-harmonically and poly-frequency vibrations [5-8]. The last will realize by the use of structural nonlinear and translation to the vibro-impact systems class. Two-frequency (by-harmocally) vibrations can be realized by the linear models at a certain structure, parameters and terms of indignation [7, 8]. The increase of power efficiency is provided by structural translation of the two-mass system in high-efficiency three-mass systems by the proper determination stiffness-inertial parameters [9]. However, without regard to considerable power advantages of such systems they remain to work in the harmonious mode, and efficiency of the system shows up only in the case of near location of eigenfrequencies and grows for diminishing of interresonance area.

Power descriptions (strengths of current and hauling force) analysis of electromagnetic contour of the impulsive chart of indignation specifies on the multi-frequency spectrum of periodic hauling force [1, 9]. The one-frequency mechanical system using only the first harmonious constituent of hauling drive force. A multiple ultraharmonics is not in a position high-quality to influence on a working process, as it is not on resonance mechanical frequencies. They are absent in principle in linear model of the two-mass system type.

Realization of resonance vibrations in the three-mass system is possible on the values of two fundamental own frequencies of vibrations [10-13], which are formed by the resilient links of high inflexibility, which connect the oscillations masses. It is necessary to provide the values of eigenfrequencies $ω_{01}$ and $ω_{02}$ by operating the inertia-stiffness parameters of the three-mass system. The presence of simple charts of feed and two eigenfrequencies of vibrations induces to such possible two-frequency modes works of vibratory machines with an electromagnetic drive with multipleness of frequencies 2. Rational amplitudes of oscillation are technologically determined [14]. Therefore, the use of impulsive charts of feed of electromagnets is of principle and has for an object the rational use of poly-frequency spectrum of pulsating hauling force on resonance by two basic harmonics [10].

4. Statement of purpose and problems of research

Researches are directed on realization of two-frequency resonance due to translation of the two-mass system to three-mass by addition partial stiffness-inertia module with a proper calculation of his parameters. A task of realization of the two-frequency modes with the proper composition of accordions and stability of resonance of one- and two-frequency systems at the different terms changes of technological factors is also important to consider.

5. The main material presentation.

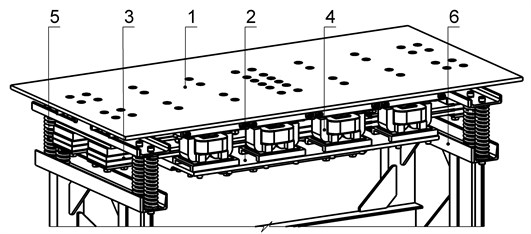
The basic linear system of vibratory table (Fig. 1) with vertical motion of the masses is certain by stiffness-inertial parameter of working 1 ( $m_{1}$ ) and reactive 2 ( $m_{2}$ ) the masses, and also by the coefficient of resiliency of package of flat springs 3, that settles accounts on condition for providing of high-frequency (100 Hz $)$ near resonance mode:

1

c_{1} = \frac{{m_{1} m_{2} (2 ω_{01})}^{2}}{(m_{1} {+ m}_{2})},

where $ω_{01} = ω / z$ – free vibrations frequency, $ω =$ 314 s^-1 – frequency of indignation, $z =$ 0,94,…, 0,98 – resonance adjusting. Oscillating masses inertia parameters $m_{1} =$ 207 kg, $m_{2} =$ 161 kg, resonance adjusting $z =$ 0,94, therefore is needed to provide the coefficient of resiliency of package of flat springs $c_{1} =$ 4,046×10⁷ N/m, which work on a bend for realization of the high-frequency mode. Alternating current electromagnets 4 apply for the power indignation of system’s vibrations. A vibratory table is set by vibration-isolating springs 5 on a frame 6.

Fig. 1The two-mass resonant vibratory table general’s view: 1 – working mass, 2 – reactive mass, 3 – package of flat springs, 4 – electromagnets, 5 – isolating springs, 6 – frame

The two-mass resonant vibratory table general’s view: 1 – working mass, 2 – reactive mass, 3 – package of flat springs, 4 – electromagnets, 5 – isolating springs, 6 – frame

Functioning of such system is approximately described the system of ordinary nonlinear differential equalizations [1-4]:

2

\{\begin{array}{l} \frac{μ_{0} S w^{2}}{2 [δ_{0} - (y_{1} (t) - y_{2} (t))]} \frac{d}{d t} i (t) + [r + \frac{μ_{0} S w^{2} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t))}{{2 [δ_{0} - (y_{1} (t) - y_{2} (t))]}^{2}}] i (t) = U_{0} \sin (ω t), \\ [\begin{matrix} [m_{1} + a ∙ m_{l o a d}] \frac{d^{2}}{{d t}^{2}} y_{1} (t) + d ∙ ω ∙ m_{l o a d} \frac{d}{d t} y_{1} (t) + c_{i z} ∙ y_{1} (t) \\ {+ b}_{i z} \frac{d}{d t} y_{1} (t) + c_{1} (y_{1} (t) - y_{2} (t)) + b_{1} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t)) \end{matrix}] = f (t), \\ m_{2} \frac{d^{2}}{{d t}^{2}} y_{2} (t) - c_{1} (y_{1} (t) - y_{2} (t)) - b_{1} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t)) = - f (t), \\ f (t) = \frac{n ∙ μ_{0} S w^{2}}{4} {[\frac{i (t)}{δ_{0} - (y_{1} (t) - y_{2} (t))}]}^{2} . \end{array}

Denotation of parameters: $w =$ 640 – spool’s number of coils; $S =$ 3,6×10^-³ m² – magnet’s area of surface of poles; $r =$ 1 Ω – pure resistance of spool; $δ_{0} =$ 0,0022 m – nominal value of air interval; $n =$ 8 – amount of parallel workings electromagnets; $U_{0} =$ 220 $\sqrt{2}$ V – tension’s nominal value; $m_{l o a d} =$ 120 kg – technological load mass; $a$ , $d$ – wave coefficients of influence of high-usage concrete mixture to oscillation of working mass [14]; $b = 2 m_{1} m_{2} ς ω / (m_{1} {+ m}_{2})$ – dumping factor of machine, in particular coefficient of viscid friction of the oscillating system, $ς$ – a parameter of fading (dimensionless coefficient of damping) of the resulted resonance system as part of size of the critical dumping for this system, $ς =$ 0,15.

Acceleration of working mass is one of basic kinematics descriptions of the system [9, 14], strength of current and hauling effort is a power’s parameters. They have harmonious sentinels descriptions at the one-frequency mode and reactive chart of feed (Fig. 2).

The influence of parameters of high-usage environment in the simplified kind on mass-dumping property of working system by the use of the erected coefficients of influence; $a$ , $d$ is so important. On this account kinematic descriptions test a substantial change and efficiency of realization of technological process is violated in the resonance modes. For their correction use adaptive control system [2, 5].

Modernization of the system foresees introduction of the additional partial oscillation module which is assembled to reactive $m_{2}$ mass, the same translating the system to the three-mass structure. Stiffness coefficient $c_{2}$ of the additional module provide two-frequency resonance mode are certain by the condition of multipleness 2 fundamental own frequencies of vibrations:

3

c_{2} = \frac{m_{2} m_{3} [17 M m_{2} - 8 m_{1} m_{3} - 5 m_{2} \sqrt{\frac{M (9 M m_{2} - 16 m_{1} m_{3})}{m_{2}}}] {ω_{01}}^{2}}{{2 (m_{1} + m_{2}) (m_{2} + m_{3})}^{2}},

where $M = m_{1} + m_{2} + m_{3}$ – total system’s mass.

Fig. 2Sentinel dependences of kinematics and power parameters of one-frequency vibratory table: a) acceleration of working mass; b) current; c) hauling effort of electromagnets; d), e), f) their spectrology

Sentinel dependences of kinematics and power parameters of one-frequency vibratory table: a) acceleration of working mass; b) current; c) hauling effort of electromagnets; d), e), f) their spectrology

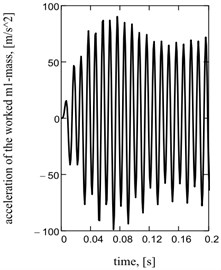
a)

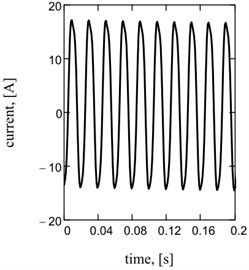
b)

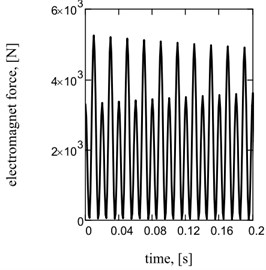
c)

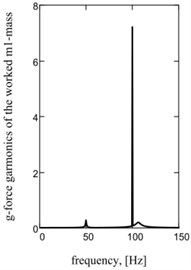
d)

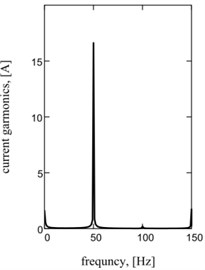
e)

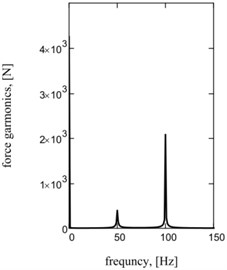
f)

The inertial value of unknown $m_{3}$ mass is determined on condition of existence of actual values of coefficient of resiliency, and can be in possible limits:

4

0 < m_{3} < \frac{{9 m}_{2} (m_{1} + m_{2})}{(16 m_{1} - 9 m_{2})} .

System of differential equalizations of motion of the three-mass vibratory system taking into account impulsive work of electromagnet on the base of chart with idealize volt-ampere description of diode:

5

\{\begin{array}{l} \frac{μ_{0} S w^{2}}{2 [δ_{0} - (y_{1} (t) - y_{2} (t))]} \frac{d}{d t} i (t) + [\begin{matrix} r + (1 - Ф [i (t)]) r_{〈+〉} + r_{〈-〉} + \\ + \frac{μ_{0} S w^{2} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t))}{{2 [δ_{0} - (y_{1} (t) - y_{2} (t))]}^{2}} \end{matrix}] i (t) = U_{0} \sin (ω t), \\ [\begin{matrix} [m_{1} + a ∙ m_{l o a d}] \frac{d^{2}}{{d t}^{2}} y_{1} (t) + d ∙ ω ∙ m_{l o a d} \frac{d}{d t} y_{1} (t) + c_{i z} ∙ y_{1} (t) \\ {+ b}_{i z} \frac{d}{d t} y_{1} (t) + c_{1} (y_{1} (t) - y_{2} (t)) + b_{1} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t)) \end{matrix}] = f (t), \\ [\begin{matrix} m_{2} \frac{d^{2}}{{d t}^{2}} y_{2} (t) - c_{1} (y_{1} (t) - y_{2} (t)) - b_{1} (\frac{d}{d t} y_{1} (t) - \frac{d}{d t} y_{2} (t)) \\ {+ c}_{2} (y_{2} (t) - y_{3} (t)) + b_{2} (\frac{d}{d t} y_{2} (t) - \frac{d}{d t} y_{3} (t)) \end{matrix}] = - f (t), \\ m_{3} \frac{d^{2}}{{d t}^{2}} y_{3} (t) - c_{2} (y_{2} (t) - y_{3} (t)) - b_{2} (\frac{d}{d t} y_{2} (t) - \frac{d}{d t} y_{3} (t)) = 0, \\ f (t) = \frac{n ∙ μ_{0} S w^{2}}{4} {[\frac{i (t)}{δ_{0} - (y_{1} (t) - y_{2} (t))}]}^{2} . \end{array}

Denotation of a new parameters: $Ф [i (t)]$ – Heaviside function, which will realize impulsive sentinel description of strength of current after the values of resistances of diode in direct $r_{〈+〉} =$ 0,001 Ω and reverse $r_{〈-〉} =$ 10⁸ Ω directions (diode’s ideal volt-ampere description); $b_{1} = γ c_{1} / ω$ , $b_{2} = γ c_{2} / ω$ , $b_{i z} = γ c_{i z} / ω$ – viscid friction coefficients in resilient elements; $γ =$ 0,025 – coefficient of internal non-resilient resistance of steel springs.

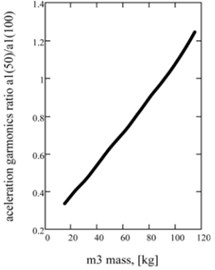
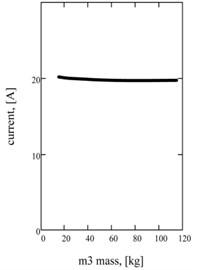
Fig. 3Influence of inertia of a mass on the two-frequency mode acceleration descriptions: а) on a maximal value; b) on a betweenness by higher and low accordions; c) on strength of current in an electromagnetic circle

Influence of inertia of a mass on the two-frequency mode acceleration descriptions: а) on a maximal value; b) on a betweenness by higher and low accordions; c) on strength of current in an electromagnetic circle

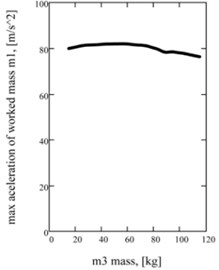
a)

b)

c)

The features of realization of two-frequency vibrations are determined influence of $m_{3}$ inertia on the peak values of multiple basic accordions of acceleration of working $m_{1}$ mass ${|A_{1}|}_{50 H z}$ and ${|A_{1}|}_{100 H z}$ , and on a maximal value $a_{1 m a x}$ . Principle dependences for descriptions of acceleration of working mass are built operating by the change of a reactive mass inertia. In particular, Fig. 3(a) is showing influence on the maximal value of acceleration of working mass, and on Fig. 3(b) – the relation of accordions of two-frequency mode. Practically the permanent value of a maximum of acceleration at the different values of reactive mass inertia is observed. Substantial influence is tested by a betweenness by the constituents of accordions. It allows to synthesize beforehand a machine with the proper harmonious composition without violation of its efficiency (by a maximum of acceleration). Power charges do not change practically, to what dependence testifies for strength of current (Fig. 3(c)).

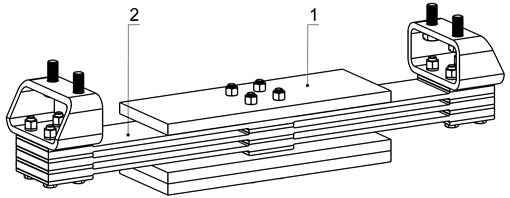
The stiffness coefficient $c_{2} =$ 2,77×10⁶ N/m of two-frequency mode is expected by the inertia value of mass $m_{3} =$ 25 kg (concordantly critical value is $m_{3 (m a x)} =$ 286,2 kg (Eq. (4))). An additional module general's view with mass 1 and the package of flat springs 2 is resulted at the figure 4. Relation between more high and low the accordions of acceleration of working mass will make for expected resiliently inertia parameters ${|A_{1}|}_{50 H z} / {|A_{1}|}_{100 H z} =$ 0,373. The recommended values and relations of accordions of acceleration in g-force for a process of vibrocompression by the two-frequency systems have a next view [14]: $1,5 g / 4 g$ ( $=$ 0,375).

Fig. 4An additional module general’s view

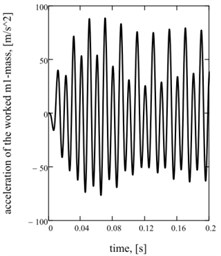
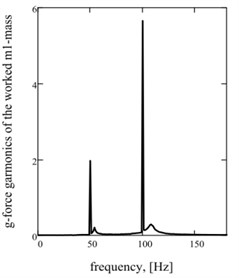
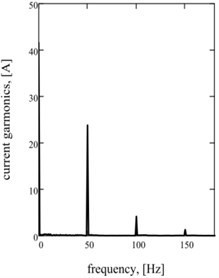
Graphic dependences of basic kinematics (Fig. 5(a) is an instantaneous acceleration of working mass) and power (impulsive) parameters (Fig. 5(b) is strength of current; Fig. 5(c) is hauling effort) confirm rationality offered approach. Impulsive character of change of strength of current and hauling force causes the display of two multiple accordions in their descriptions Fig. 5(d)-(f).

Fig. 5Sentinel dependences of kinematics and power parameters of two-frequency vibratory table: a) acceleration of working mass; b) current; c) hauling effort of electromagnets; d), e), f) their spectrology

Sentinel dependences of kinematics and power parameters of two-frequency vibratory table: a) acceleration of working mass; b) current; c) hauling effort of electromagnets; d), e), f) their spectrology

а)

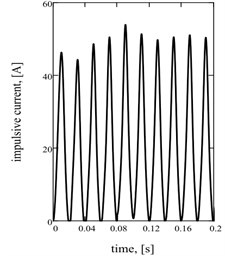
b)

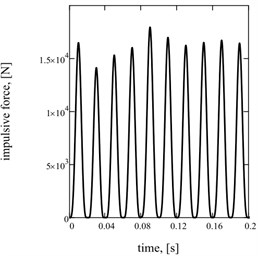
c)

d)

e)

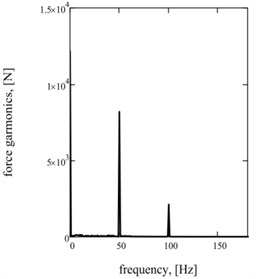
f)

Authenticity of realization of multiple resonance two-frequency mode with the set value of acceleration of working mass on the proper frequencies specifies frequency description (Fig. 6) is built by the change of frequency of tension of feed of electromagnets.

Fig. 6Acceleration’s frequency description of working mass of two-frequency resonance machine (a=d= 0,5)

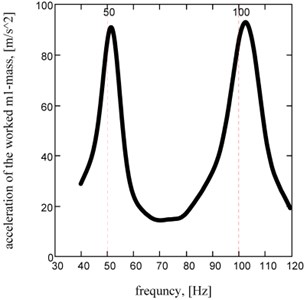
The analysis of technological firmness is setting the sensitiveness of kinematics parameters to the changes of mechanical descriptions is important direction of research of the resonance oscillation systems. An environment influences on inertia-dumping property of the oscillating system by technological coefficients $a$ and $d$ is accepted. The analysis of their influence on changing of a maximum of acceleration of working mass in relation to an unhigh-usage machine (if $a = 0$ and $d = 0$ ) is carried out. Graphic dependences (Fig. 7) specify on higher firmness of the two-frequency resonance system, on condition of change of inertia-dumping coefficients scope $a =$ 0,…, 1 and $d =$ 0,…, 2. It is additional substantial technological advantage of the two-frequency systems above one-frequency, and specifies on efficiency of their use.

Fig. 7The relative change of the acceleration for the variable technological coefficients: a= 0,…, 1, d= 0,…, 2

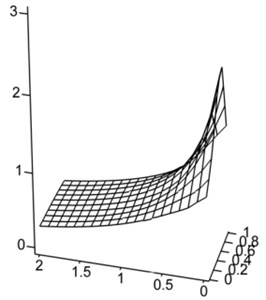
a) One-frequency system

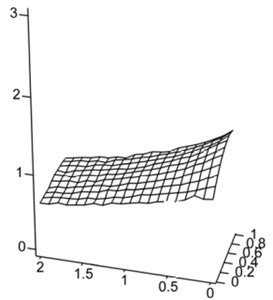
b) Two-frequency system

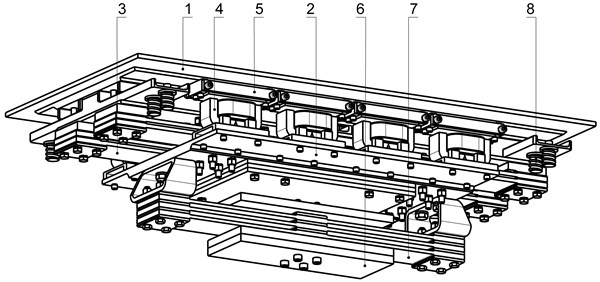
Offered vibratory table by the structural implementation selected the presence of the third oscillation mass 6, that by the package of flat springs 7 fastened to mass 2 (Fig. 8). Other structural parameters of the system in relation to it initial model, in particular working mass 1, package of flat springs 3, core 4 with anchors 5 electromagnets (Fig. 1) are unchanging. Passing to the impulsive chart of indignation is principle due to the use in the electromagnetic contour of rectifier diode.

Fig. 8Oscillation system of the two-frequency resonant vibratory table general’s view

6. Conclusions

Modernization of harmonically resonance machines is provided introduction partial stiffness-inertia module, expected by offered approach. Thus technological possibilities of machine get better substantially, in particular quality of treatment and firmness to the changes of terms of loading. The followings dynamic features of such machines are set as:

1) two higher fundamental own frequencies, that become the proper calculation of stiffness parameter and inertia description of the added mass multiple 2;

2) the added mass inertia determines the peak values of multiple harmonics acceleration of working mass, that allows to synthesize machines with the proper composition of dynamic parameters;

3) the added mass inertia doesn’t influence on a maximum value of working mass acceleration and energy consumption of machine;

4) two-frequency resonance mode can be realized by the use of impulsive indignation of electromagnetic vibroexciters in the three-mass system with an according stiffness-inertia parameters.

References

Despotovic Zeljko V., Stojiljkovic Zoran V. PSPICE Simulation of two-mass vibratory conveying system with electromagnetic drive. EUROCON, Serbia and Montenegro, Belgrade, 2005.

Search CrossRef
Despotovic Zeljko V., Stojiljkovic Zoran V. Power converter control circuits for two-mass vibratory conveying system with electromagnetic drive: simulations and experimental results. IEEE Transactions on Industrial Electronics, Vol. 54, Issue 1, 2007, p. 453-466.

Search CrossRef
Tentor Lawrence B. Characterization of an Electromagnetic Tuned Vibration Absorber. Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctorate of Philosophy in Mechanical Engineering, Blacksburg, Virginia, http://scholar.lib.vt.edu/theses/available/etd-05272002-194631/unrestricted/01Dissertation.pdf, 2001.

Search CrossRef
Behrens S., Fleming A. J., Moheimani S. O. R. Vibration isolation using a shunted electromagnetic transducer. Proceedings of Smart Structures and Materials: Damping and Isolation, Vol. 538, 2004, p. 506-515.

Search CrossRef
Sokolov I. J., Babitsky V. I., Halliwell N. A. Autoresonant vibroimpact system with electromagnetic excitation. Journal of Sound and Vibration, Vol. 308, 2007, p. 375-391.

Search CrossRef
Babitsky V. I., Sokolov I. J. Autoresonant homeostat concept for engineering application of nonlinear vibration modes. Nonlinear Dynamics, Vol. 50, 2007, p. 447-460.

Search CrossRef
Bukyn S. L., Maslov S. G., Lyuty А. P., Reznichenko G. L. Intensification of processes through the implementation of vibrators biharmonic modes. Mineral Processing, Vol. 36-37, 2009, p. 81-89, (in Russian).

Search CrossRef
Goncharevich I. F. About the performance and efficiency increase for industrial nanotechnologies. Nanotechnologies in Construction: A Scientific Internet Journal, Vol. 1, Issue 3, 2009, p. 36-49, (in Russian).

Search CrossRef
Lanets O. S. Highly Inter-Resonance Vibrating Machines with an Electromagnetic Drive (Theoretical Bases and Practice of Creation). Monograph, Publishing House of the Lviv Polytechnic National University, Lviv, 2008, p. 324, (in Ukrainian).

Search CrossRef
Borschevskyy A. A., Sanko O. L. Pat. 645910 S.U. Data of Patent: 2/1975. Biharmonic Electromagnetic Exciter. 1975, (In Russian).

Search CrossRef
PopperBoaz Pat. 5,144,176 U.S. Data of Patent: 4/1990. Three-Mass Electromagnetic Vibrating System. 1990.

Search CrossRef
Brown William R. Pat. 4,378,064 U.S. Data of Patent: 3/1983. Three Mass Electromagnetic Feeder. 1983.

Search CrossRef
Falconer Thomas H. Pat. 4,961,491 U.S. Data of Patent: 9/1990. Three Mass Vibratory Feeder. 1990.

Search CrossRef
Nazarenko I. I. Vibrating Machines and Processes of Construction Industry. KNUCA, Kyiv, 2007, p. 229, (in Ukrainian).

Search CrossRef

About this article

Received

02 September 2015

Accepted

05 October 2015

Published

30 December 2015

Keywords

vibratory table

electromagnetic drive

resonance

oscillation system

eigenfrequencies

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.