Abstract
A new method is proposed to calculate natural frequencies of a rectangular variable cross-section beam with multiple cracks under different temperatures. The temperature module is introduced through the elastic modulus, and cracks are modelled by bending springs without mass. Based on the transfer matrix method, the characteristic equation of the cracked beam is derived by the implementation of different boundary conditions. Examples are presented on cantilever beams having different non-uniformity parameters, and the influence of the temperature, the number and geometric parameters of cracks on natural frequencies is also investigated. Compared with results obtained using the Patran FEM method, good agreements are obtained and this analytical method is demonstrated to be feasible.
1. Introduction
With the rapid development of science and technology, more and more mechanical equipments are developing towards high speed, high temperature and high pressure, so the application of high temperature alloy material is becoming more and more extensive. In the practical engineering of architecture, bridge and aerospace, beam structures have been widely used, including beams of uniform cross-section and variable cross-section. Empirical performance has proved that variable cross-section beams show better mechanical properties than uniform cross-section beams, therefore people pay more and more attention to the application prospect of variable cross-section beams.
At present, some achievements have been made on the free vibration of the variable cross-section beams. Gupta A. K. [1] used the finite element method to calculate natural frequencies of the linearly tapered beam with any cross-sectional shape. Alshorbagy et al. [2] investigated dynamic behaviors of the functional graded beam by the numerical finite element method. References [3, 4] used ADM (Adomian decomposition method) to analyze the transverse vibration of the stepped beam. De Rosa et al. [5] performed the free vibration analysis of variable circular cross-section column by DQM and CDM. Huang and Li [6] transformed the govering differential equation to the corresponding Fredholm integral equations, and proposed a new analytical method to analyze the free vibration of axially graded and non-uniform beams. Ahmad Shahba [7] developed a new method called DTEM to analyze the free vibration and stability of tapered Euler-Bernoulli beams based on DTM. Ece M. C., Aydogdu M. and Taskin V. [8] studied vibration characteristics of the rectangular variable cross-section beam with the exponential formed section width. Laura P. A. A., Gutierrez R. H. and Rossi R. E. [9] applied an approximate numerical method to determine natural frequencies of the Euler-Bernoulli beam, which has a rectangular cross-section of the constant width and bilinearly varying thickness. Caruntu D. [10] studied nonlinear vibration problems of rectangular section beams with parabolic thickness variation. Elishakoff and Johnson [11] investigated the transverse vibration of a beam which has axially non-uniform material properties; this is a special case of variable cross-section beams. However, researches above only investigated vibration characteristics of variable cross-section beams under room temperature, and neglected the effect of the temperature and initial cracks on the free vibration of the beam.
Due to the processing and assemblage, beams have some initial damages of different degree. The most common form of structural damages is the crack, which will change dynamic characteristics of beams such as natural frequencies and mode shapes. Such changes are dependent on the number, positions and depths of cracks. Therefore, the calculation of natural frequencies of the cracked beam is an important aspect of analyzing the beam vibration and stability. Many researches have been devoted to this area [12, 13]; however, these studies are limited to the beam with only one single crack. Ostachowicz W. M. and Hu J. [14-15] have done some studies on the influence of multiple cracks on structural dynamic characteristics; these methods used are very complicated at high orders of the characteristic determinant of the structure. Shifrin E. I. and Ruotolo R. [16] reduced the order of the characteristic determinant effectively, and developed a modified method to calculate the natural frequency of the constant section beam with multiple cracks. However, these studies only investigated uniform cross-section beams under room temperature, and didn’t incorporate the influence of the temperature and variable cross-section. At present, there are no methods to calculate natural frequencies of variable cross-section beams with multiple cracks under different temperatures.
In this paper, a new method for evaluating natural frequencies of rectangular variable cross-section beams with multiple cracks is investigated under different temperatures. The temperature module is introduced through the elastic modulus, and cracks are modeled by bending springs. Based on the use of the transfer matrix method and the Euler-Bernoulli beam theory, a 4×4 transfer matrix with geometric parameters of cracks and cross-section parameters of the whole beam can be derived. Natural frequencies of the beam can be easily obtained by the implementation of boundary conditions, and its validity is confirmed by comparison with natural frequencies evaluated by the Patran FEM method.
2. Establishment of the model
Shown in Fig. 1 is an isotropic and rectangular variable cross-section beam with transverse cracks. It’s assumed that these cracks are all macroscopic open cracks, and always keep open, which can be described by the linear elastic fracture mechanics. The length of the beam is , and the width and height of each cross-section are and respectively, where is the position along the horizontal axis in the coordinate system. Depths of cracks are , ,…, , and positions of cracks are , ,…, . In order to simplify the calculation, the inflation rate of the beam is negligible under different temperature.
According to the theory of Dimarogonas and Paipeties [17], the local flexibility of each crack on the beam can be expressed as:
where 1, 2,…, ; is the local flexibility of crack No. under different temperatures; is the Young’s modulus under different temperatures; is the height of the cross-section where the crack No. is located; is the moment of inertia of the cross section where the crack No. is located; is the relative depth of crack No. ; is the local flexibility function of crack No. , which can be obtained through the strain energy density function:
where [0, 0.6].
Considering each transverse crack as an endpoint of the beam, the whole beam is divided into sections by cracks, and each section is an intact beam with length (1, 2,…, ). The free vibration differential equation without damping of Euler-Bernoulli beam can be expressed as:
where and are the area and the moment of inertia of the cross section of the beam; is the density of the beam under different temperatures.
Fig. 1Model of the beam with multiple cracks
According to Mehmet’s paper [4], as shown in Fig. 2, dimensionless variables are defined according to:
where is the dimensional time; is the dimensional coordinate measured from the left end of the beam No. along its length, and are the dimensional area and moment of inertia of the cross-section of the beam No. respectively, is the dimensional transverse displacement, is the length of the beam No. , is any reference displacement and and are respectively the area and moment of inertia of the cross-section of the beam No. . At the left end (where ), , . The governing equation in the dimensionless form of each intact beam can be written as follows:
where .
According to the principle of modal analysis, the solution of the Eq. (5) can be assumed in the following form of variables separation:
Substitution of Eq. (6) into Eq. (5) yields two ordinary differential equations:
where is a real constant and defined as , and is radial frequency under different temperatures.
Solution of Eq. (8) is well known and can be written as:
Solution of Eq. (7) requires the geometry of the cross-section of the beam to be specified, and the geometry of the cross-section is rectangular and given that and through the coordinate system in Fig. 2. Here is the non-uniformity parameter of the variable cross-section beam, and .
For the family of the cross-sections with constant height and exponentially varying width, Eq. (7) reduces to:
The solution of Eq. (10) can be obtained as:
where: , .
Fig. 2Model of each intact beam
3. Establishment of the transfer matrix
According to Mechanics of Materials, the angle of deflection , the bending moment and the shearing force can be obtained as follows:
At the left end of each intact beam, the above formulas are used and the deflection, the angle of deflection, the bending moment and the shearing force are obtained:
Transforming the equations into the matrix form:
Similarly, at the right end of each intact beam, the above formulas are used and the deflection, the angle of deflection, the bending moment and the shearing force are obtained:
Transforming the equations into the matrix form:
Substitution of Eq. (14) into Eq. (16) yields the equation of each intact beam:
where is the transfer matrix of the intact beam No. under different temperatures.
At the location of the crack No. , according to the interrelation of the deflection, the angle of deflection, the bending moment and the shearing force between the left and right surfaces of the crack, the transfer matrix of the crack No. can be obtained:
where is the transfer matrix of the crack No. under different temperatures.
So for the whole beam with transverse cracks, the transfer relationship between state vectors of the right end and left end can be written as:
where:
The matrix is called the transfer matrix of the whole beam with transverse cracks under different temperatures. In the general case, two of the boundary conditions are equal to zero when applying boundary conditions listed in Ref. [19], hence a 2×2 characteristic matrix is obtained. The equation for calculating the natural frequency of the whole beam can be expressed as:
From Eq. (22), the natural frequency of each order of the whole beam can be calculated and the corresponding inherent vibration mode can be obtained by Eq. (11).
4. Finite element model
A finite element simulation software (Patran) would be used to establish the geometric mesh model of the cracked variable cross-section beam, and natural frequencies from normal modes analysis would be compared with results from the theoretical method proposed in this paper. It’s assumed that the variable cross-section beam is a cantilever beam, and the mesh model of the cracked beam can be built by setting boundary conditions. The models of the variable cross-section beam with different numbers of cracks are shown in Fig. 3.
Fig. 3Model of the cracked variable cross-section beam

a) Model of the variable cross-section beam with one crack

b) Model of the variable cross-section beam with two cracks

c) Model of the variable cross-section beam with three cracks
5. Results and discussion
Using the cantilever beam as an example, the geometric parameters of the beam is as follows according to the coordinate system of Fig. 1: 10 m, m, m. The structural material is the low carbon alloy steel AISI1050, with material parameters of 210 GPa, 7860 kg/m3. According to the Ref. [18], the density of the structural steel is very little affected by the temperature, and its value at high temperature is the same as that under room temperature; the elastic modulus under different temperatures can be calculated as follows: , and is the proportional coefficient of the elastic modulus under different temperatures:
where is the temperature, [0, 600 °C].
(1) Consider the natural frequency ratio () as the research object, where 1, 2, 3, 4; is the natural frequency of the order No. with the different non-uniformity parameters ; is the natural frequency of the order No. with the non-uniformity parameter . It is assumed that the temperature 20 °C, the non-uniformity parameter [–2, 2] and there is no crack on the cantilever beam. Variations of the tranverse vibration natural frequency ratios of a non-uniform beam with exponentially varying width are shown in Fig. 4.
Fig. 4Variation of natural frequencies of the beam with different non-uniformity parameters
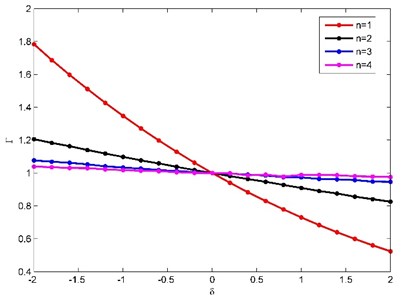
The Fig. 4 is the same with the Fig. 3 in Ref. [4], therefore the transfer matrix of the whole beam is correct. The natural frequency of each order gradually decreases as the non-uniformity parameter increases; and the amplitude of the decrease gradually decreases as the order of natural frequencies increases; and the influence of the non-uniformity parameter on the natural frequency gradually decreases as the order of the natural frequency increases.
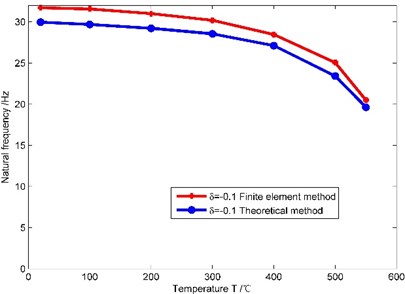
(2) It is assumed that there is no crack on the cantilever beam, and the temperature 20 °C, 100 °C, 200 °C, 300 °C, 400 °C, 500 °C, 550 °C and the non-uniformity parameter –0.1, 0, 0.1. Natural frequencies obtained through the theoretical method and the finite element method are shown in Fig. 5.
Fig. 5Natural frequencies of the beam obtained by the theoretical method and the finite element method
a)–0.1
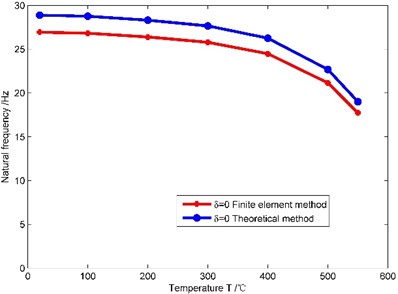
b)0
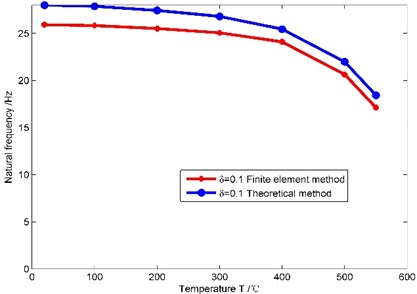
c)0.1
As shown in Fig. 5, when the non-uniformity parameter has different values, natural frequencies obtained by the theoretical method and the finite element method are very close under different temperatures, and the maximum error is 7.4 %. So the theoretical method proposed in this paper is feasible. When the non-uniformity parameter remains unchanged, the first order natural frequency of the beam gradually decreases as the temperature increases, and the amplitude of the decrease gradually increases as the temperature increases
(3) It is assumed that there is no crack on the cantilever beam, and the temperature [0, 600 °C] and the non-uniformity parameter [–2, 2]. The first order natural frequencies of the variable cross-section beam with different temperatures and non-uniformity parameters are shown in Fig. 6.
Fig. 6Variation of the natural frequency of the cracked beam with different temperatures and non-uniformity parameters (Mode 1)
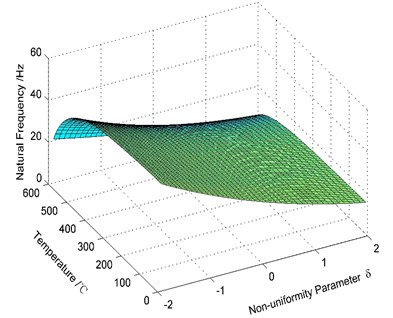
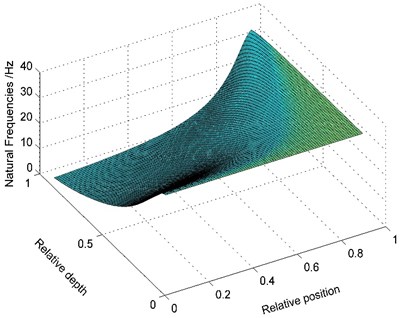
Fig. 7Variation of natural frequencies of the cracked beam with different geometric parameters of the crack (Model 1)
As shown in Fig. 6, the relationship between the first order natural frequency of the beam and the temperature and the non-uniformity parameter is described. When the non-uniformity parameter remains unchanged, the natural frequency of the beam gradually decreases as the temperature increases, and the amplitude of the decrease gradually increases as the temperature increases. When the temperature [0, 300 °C], the amplitude of the decrease is real small; when the temperature [300 °C, 600 °C], the high temperature has a larger effect on the natural frequency of the beam.
(4) It is assumed that there is only one transverse open crack on this cantilever beam, and the temperature20 °C and the non-uniformity parameter –1. When the crack has different relative position and relative depth, the first order natural frequencies of the variable cross-section cracked beam are shown in Fig. 7.
As shown in Fig. 7, the relationship between the first natural frequency and geometric parameters of the crack is described. Both of the relative depth and relative position of the crack have a significant effect on the natural frequency of the beam. When the relative position of the crack remains unchanged, the first order natural frequency gradually decreases as the relative depth of the crack increases; and when the relative depth of the crack remains unchanged, the first order natural frequency gradually increases as the relative position of the crack increases.
(5) It is assumed that the non-uniformity parameter 0.1 and values of the temperature are shown as follows: 20 °C, 100 °C, 300 °C, 500 °C . Consider four more different cases:
• There is no transverse crack on the cantilever beam.
• There is only one transverse crack on the cantilever beam, and geometric parameters of the crack are as follows: 0.1, 0.5.
• There are two transverse cracks on the cantilever beam, and geometric parameters of cracks are as follows: 0.1, 0.5; 0.2, 0.5.
• There are three transverse cracks on the cantilever beam, and geometric parameters of cracks are as follows: 0.1, 0.5; 0.2, 0.5; 0.3, 0.5.
The first order natural frequencies of the beam obtained through the finite element method (FEM) and the theoretical method (TM) in these four cases are shown in Table 1.
Table 1Natural frequencies of the beam with different number of cracks under different temperatures (Unit: Hz)
Number of cracks | 20 °C | 100 °C | 300 °C | 500 °C |
0 (FEM) | 25.912 | 25.827 | 25.062 | 20.64 |
0 (TM) | 27.9952 | 27.8738 | 26.8004 | 21.9899 |
1 (FEM) | 9.902 | 9.8597 | 9.4794 | 7.7779 |
1 (TM) | 9.2853 | 9.2457 | 8.8899 | 7.2942 |
2 (FEM) | 9.0481 | 9.0032 | 8.656 | 7.1023 |
2 (TM) | 8.5359 | 8.4994 | 8.1717 | 6.7049 |
3 (FEM) | 8.5916 | 8.5549 | 8.225 | 6.7487 |
3 (TM) | 8.3245 | 8.2889 | 7.9693 | 6.5388 |
Comparison of the first order natural frequencies obtained by the finite element method and the theoretical method in different cases is shown in Table 1. FEM results and TM results are very close, and the maximum error is 7.4 % when the beam has no crack on the beam under the temperature 100 °C, so the theoretical method proposed in this paper is feasible. When the temperature remains unchanged, the first order natural frequency of the beam gradually decreases as the number of cracks increase, and cracks have a great influence on the natural frequency of the beam.
6. Conclusions
In this paper, a simple and efficient method for evaluating natural frequencies of a rectangular variable cross-section beam with multiple cracks has been developed under different temperatures. Using this method, the transfer matrix of a variable cross-section beam with multiple cracks was derived, which was related to the temperature, geometric parameters of cracks and cross-section parameters of the whole beam, then natural frequencies of the beam was obtained by the implementation of the boundary conditions.
The proposed analytical method was validated using the Patran FEM software, which was used to build geometric and mesh models of the variable cross-section cracked beam. Natural frequencies of the variable cross-section cracked beam obtained via the two methods were extremely similar, with a maximum percent error of 7.4 %.
The advantage of this method is that it can be applied to the beams under various boundary conditions. There is no need to derive the analytic solution of natural frequencies of the cracked beam, and natural frequencies can be solved directly through the transfer matrix.
References
-
Gupta A. K. Vibration of tapered beams. Journal of Structural Engineering, Vol. 111, Issue 1, 1985, p. 19-36.
-
Alshorbagy A. E., Eltaher M. A., Mahmoud F. F. Free vibration characteristics of a functionally graded beam by finite element method. Applied Mathematical Modelling, Vol. 35, Issue 1, 2011, p. 412-425.
-
Mao Q., Pietrzko S. Free vibration analysis of stepped beams by using Adomian decomposition method. Applied Mathematics and Computation, Vol. 217, Issue 7, 2010, p. 3429-3441.
-
Mao Q. Free vibration analysis of multiple-stepped beams by using Adomian decomposition method. Mathematical and Computer Modelling, Vol. 54, Issue 1, 2011, p. 756-764.
-
De Rosa M. A., Martín H., Maurizi M. J., et al. Vibraciones libres de una torre de sección variable con vínculos elásticos en su base y una masa excéntrica con inercia rotacional en el extremo superior. Revista Iberoamericana de Ingeniería Mecánica, Vol. 15, Issue 2, 2011, p. 55-64, (in Spanish).
-
Huang Y., Li X. F. A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. Journal of Sound and Vibration, Vol. 329, Issue 11, 2010, p. 2291-2303.
-
Shahba A., Rajasekaran S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials. Applied Mathematical Modelling, Vol. 36, Issue 7, 2012, p. 3094-3111.
-
Ece M. C., Aydogdu M., Taskin V. Vibration of a variable cross-section beam. Mechanics Research Communications, Vol. 34, Issue 1, 2007, p. 78-84.
-
Laura P. A. A., Gutierrez R. H., Rossi R. E. Free vibrations of beams of bilinearly varying thickness. Ocean Engineering, Vol. 23, Issue 1, 1996, p. 1-6.
-
Caruntu D. On nonlinear vibration of nonuniform beam with rectangular cross-section and parabolic thickness variation. IUTAM/IFToMM Symposium on Synthesis of Nonlinear Dynamical Systems, Springer, Netherlands, 2000, p. 109-118.
-
Elishakoff I., Johnson V. Apparently the first closed-form solution of vibrating inhomogeneous beam with a tip mass. Journal of Sound and Vibration, Vol. 286, Issue 4, 2005, p. 1057-1066.
-
Morassi A. Crack-induced changes in eigenparameters of beam structures. Journal of Engineering Mechanics, Vol. 119, Issue 9, 1993, p. 1798-1803.
-
Qian G. L., Gu S. N., Jiang J. S. The dynamic behaviour and crack detection of a beam with a crack. Journal of Sound and Vibration, Vol. 138, Issue 2, 1990, p. 233-243.
-
Ostachowicz W. M., Krawczuk M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. Journal of Sound and Vibration, Vol. 150, Issue 2, 1991, p. 191-201.
-
Hu J., Liang R. Y. An integrated approach to detection of cracks using vibration characteristics. Journal of the Franklin Institute, Vol. 330, Issue 5, 1993, p. 841-853.
-
Shifrin E. I., Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks. Journal of Sound and Vibration, Vol. 222, Issue 3, 1999, p. 409-423.
-
Dimarogonas A. D., Paipetis S. A. Analytical Methods in Rotor Dynamics. Applied Science Publishers, London, 1983.
-
European Recommendations for the Fire Safety of Steel Structures. ECCS, 1983.
-
Tong X., Tabarrok B., Yeh K. Y. Vibration analysis of Timoshenko beams with non-homogeneity and varying cross-section. Journal of Sound and Vibration, Vol. 186, Issue 5, 1995, p. 821-835.
About this article
This work is supported by a project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
