Non-sinusoidal magnetoelastic waves in structural members

1. Introduction

To improve vibrational safety of environment by electromagnetic control of machines vibration and creation of new magnetorheological materials it is necessary to formulate and solve a huge number of problems of both magnetic hydrodynamics of non-Newtonian fluids and magneto-elasticity of structural members. Remind that the magneto-elastic effect was discovered by Italian physicist E. Villary in 1865. However, magnetoelasticity as a scientific area, that emerged at the junction of solid mechanics, electrodynamics and acoustics, began to develop rapidly in the late 50-es of XX century. The first works were initiated by geophysics problems, namely the need to describe wave dynamics of deep layers of the Earth because of its conductivity and interaction with the geomagnetic field [1]. Since then dynamic processes in the interaction of electromagnetic fields and deformation have been actively studied. This is due to many physical, technical and technological applications, among of which are the problems of strength of structures and mechanisms operating in conditions of strong magnetic fields where Ampere forces resulting from the interaction of magnetic fields and currents can significantly effect on strength properties. Contactless excitation of oscillations and waves solves many technological problems in defectoscopy and vibro-processing of solidifying melts [2, 3].

Inclusion of different physical nature fields into mechanical systems opens new possibilities for development of engineering and technology [4-7]. Effects of magnetoelasticity occur in strong magnetic fields if generated loads can significantly affect wave and dissipative properties of the medium or in thin bodies: rods, plates and shells [8, 9]. Magnetoelastic medium is characterized by anisotropy of its properties created by a magnetic field. Magnetic field in a medium with finite conductivity causes an additional dissipation mechanism. These properties of magnetoelastic systems open new possibilities of practical application.

In this work a propagation of longitudinal waves in a homogeneous nonlinear superconducting rod placed in strong magnetic field is studied. The Bishop model is used to describe rod oscillation. In addition to Bernoulli model this takes into account kinetic energy of transverse motion of rod particles and potential energy of shear strain.

2. Equations of magnetoelasticity of rod

In magnetoelsticity it is proposed that electromagnetic field acts on deformation field by the Lorenz forces:

which are introduced into equations of motion:

here $\overrightarrow{E}$ – electric field intensity, $\overrightarrow{B}$ – magnetic induction vector; $\overrightarrow{j}$ – current density vector; ${\rho }_e$ – bulk density of electric charges; $\overrightarrow{u}$ – displacement vector; $\lambda$, $\mu$ – elastic moduli of second order (Lame constants); $\rho$ – material density; $\tau$ – time. Vector ${\overrightarrow{F}}_{nl}$ includes terms due to elastic nonlinearity. In case of only quadratic nonlinearity is taken into account, the vector components are expressed in terms of displacements gradient [10]:

where $A$, $B$, $C$ – are third order elastic constants (Landau moduli), index after the comma means differentiation with respect to the corresponding coordinates; repeated indices are summed.

From the Maxwell equations we obtain equations for electric $\overrightarrow{D}$ and magnetic $\overrightarrow{B}$ inductions:

which are together with equations of state:

need to be added to Eqs. (1)-(2). Here $\overrightarrow{H}$ – magnetic intensity, $\sigma$ – conductivity, ${\epsilon }_e$ – dielectric permittivity and ${\mu }_e$ – magnetic permeability of medium.

As it is common for magnetoelasticity we neglect bias currents $\partial \overrightarrow{D}/\partial \tau =0$ and consider absence of electric charges ${\rho }_e=0$ [8]. Then equations of magnetoelasticity will be written as follows:

Consider propagation of longitudinal waves in a homogeneous, non-linear elastic rod placed in an external magnetic field. Along with engineering (classical) models of rod’s dynamics a so-called refined or non-classical model are also known [11]. These models take into account additional factors affecting dynamic process or are free from some of the hypotheses adopted in engineering theory and limited their applicability. The Bishop model, by taking into account the additional kinetic energy of the transverse motion of the rod particles and the potential energy of shear strain, generalizes an adopted in describing the longitudinal vibrations of rod model based on classical theory of Bernoulli.

We assume that external magnetic field of intensity $H_0$ is perpendicular to the direction of wave propagation (Fig. 1).

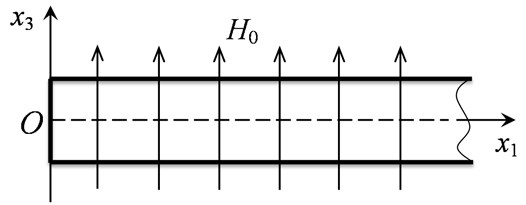
Fig. 1. Direction of external magnetic field of intensity $H_0$ with respect to longitudinal axis of the rod $O{x}_1$

The total magnetic field consists of a constant value and its disturbances occurring as a result of interaction with strain field:

where $\overrightarrow{n}$ – vector of normal, $\overrightarrow{h}$ – a small perturbation of the magnetic field.

For longitudinal waves in the rod:

Then system of equations of magnetoelasticity for the Bishop model of rod takes the form:

here $V=\partial u_1/\partial \tau$, $U=\partial u_1/\partial x_1$, $\nu$ – Poisson’s ratio, $R=\sqrt{J_0/F}$ – polar radius of inertia, $J_0=\underset{F}{\overset{}{\iint }}\left(x_2^2+x_3^2\right)dF$ – polar moment of inertia, $F$ – cross-sectional area of the rod, $E=\mu \left(3\lambda +2\mu \right)/\lambda +\mu$ – Young’s modulus, ${\alpha }_1=E/2+3\lambda /2+A+B\left(1-2\nu \right)+C/3\left(1-6\nu \right)$ – elastic nonlinearity factor, $c_0=\sqrt{E/\rho }$ – longitudinal wave velocity, $c_{\tau }=\sqrt{\mu /\rho }$ – shear wave velocity, $c$ – speed of light in vacuum.

We assume that the rod is a semi-infinite. Such idealization is acceptable if there is a disturbance source at one boundary of the rod and an optimal absorber at the second boundary, i.e. boundary conditions are so that no disturbance is reflected. In [12] on the basis of exact solutions of model problems for elastic systems the existence of the agreed end absorbers of different types of vibrations which do not reflect any disturbance in the system is justified. It allows to consider the model of rod Eq. (12) without taking into account the boundary conditions, and to consider vibrations propagating along the rod as traveling waves.

Let us pass to dimensionless variables in Eq. (12):

and introduce moving coordinate system:

where $V_p$ – characteristic velocity of the waves, unknown in advance, $\epsilon$ – small parameter.

Substitute Eqs. (13)-(14) in Eq. (12) while keeping the members with $\epsilon$ in power not higher than the first. The zero order approximation in the small parameter will determine the speed:

The first order approximation leads to the following system of equation:

where $c_A=\sqrt{H_0^2/4\pi \rho }$ – Alfven wave velocity, and:

We can see, that evolution of strain field $u$ is described by Korteweg-de Vries equation (KdV) Eq. (16), and evolution of disturbed magnetic field $h$ – by Burgers equation Eq. (17). These equations are nonlinearly coupled in dynamic problem of magnetoelasticity. Nonlinear terms are included asymmetrically in Eqs. (16)-(17): strain field affects the magnetic field parametrically, while the magnetic field is a non-linear source of strain field.

In the approximation of an infinite conductivity of rod material and stationary magnetic field the system of equations Eqs. (16)-(17) transforms to the form:

3. Nonlinear stationary waves

From second equation of system Eq. (18) we obtain relation between strain and magnetic field intensity $h=c/u$, where $c=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$. Substituting this relation to the first equation of the system and passing to the traveling waves $\mathrm{\xi }=x-V_{s}t\text{,}$ where $V_s=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\text{,}$ after integration by $\xi$ we obtain:

here ${a=-V}_s<0$, $b=$±1, and $c$ – arbitrary constant opposite in sign to $b$. Introduce the following change of variables $w=au$, $\xi =\sqrt{\left|a\right|}\eta$, then Eq. (19) take the form:

where $S_a=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(a\right)$, $S_b=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(b\right)$.

Then from Eq. (20) we obtain two equations different from each other only by the sign in front nonlinear terms. So for $b=$1 and $c<$0 Eq. (20) take the form:

here $\alpha =-c/a^4>0$. In the second case for $b=$–1 and $c>$0 Eq. (20) take the form:

where $\beta =c/a^4>0$.

First of all we consider Eq. (21) having the first integral in the form:

which can be interpreted as the energy conservation law for anharmonic oscillator. Here $E$ – is the integration constant meaning the initial energy of the system, and function $f\left(w\right)=-w^2/2-u^3/3+\alpha w^{-1}$ means potential energy. For $\alpha >\text{0}$ potential energy function has two branches, one of which reaches its minimum at $w=w_0<\text{0}$ and the second reaches its maximum at $w=w_1>\text{0}$. Numerical values of equilibrium positions $w_0$ for different values of parameter $\alpha$ are shown in Table 1.

On the phase plane $\left(w,dw/d\eta \right)$ a point of minimum potential energy with coordinates $\left(w_0,f\left(w_0\right)\right)$ corresponds to a stable equilibrium position of the “center” type. Note that function of the potential energy for Eq. (22) has a similar form as for Eq. (21). Herewith it is symmetrical with respect to the axis $w=0$; i.e. it has minimum at point $w=-w_0>\text{0}$, and maximum at point $w=-w_1<\text{0}$. In this equation the stable equilibrium position of the “center” type corresponds to the point $\left(-w_0,f\left(-w_0\right)\right)$. Therefore, periodic solutions of Eqs. (21)-(22) near position of equilibrium are the same so we further restrict ourselves to study Eq. (21).

Finding the exact solution of Eq. (21) is associated with certain difficulties. To simplify the problem we write the expansion of Eq. (21) near the equilibrium position, i.e. in powers of $\left(w+w_0\right)$. Then it takes the form:

where ${\omega }_0^2=-\left(1+2w_0+2\alpha w_0^{-3}\right)$, $p=1-3\alpha w_0^{-4}$, $q=-4\alpha w_0^{-5}.$

Solution of Eq. (24) is described by elliptic sine:

where $A_0=\sqrt{2}ms/\sqrt{-q}$ - amplitude of stationary wave, $m$ – nonlinear analogue of wave number ($m^2=\left(3{\omega }_0^2/q-p^2\right)/3q\left(1+s^2\right)$), $s^2$ – square of elliptic function modulus changing in the range of $0\le s^2\le 1$ and determining wave form. Elliptic function modulus equals zero is characteristic for linear processes. In this case elliptical sinus turns into trigonometric sine and stationary wave is harmonic. If the module is close to unity, then the periodic wave has a meander shape (Fig. 2). If the module is equal to one, then the elliptic sine transforms into the hyperbolic tangent, in this case stationary wave is solitary (soliton) and represents a jump from one constant value to another (Fig. 3).

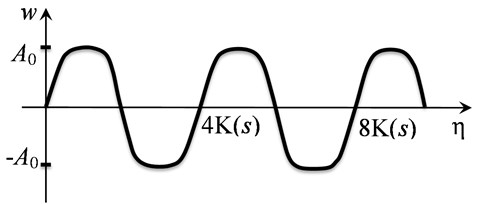
Fig. 2. Periodic wave shape at $s^2\to 1$ ($K\left(s\right)$ denotes complete elliptic integral of the first kind)

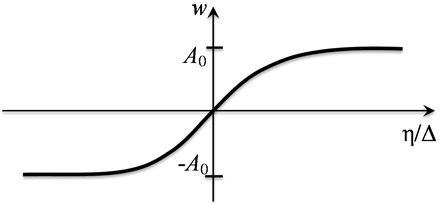
Fig. 3. Solitary wave shape

Numerical values of equations coefficients depending on the parameter $\alpha$ are in the Table 1. It shows that the values of $p$ can be both positive and negative. In particular, for $\alpha =\text{1.6}$ and $p=\text{0}$ Eq. (24) turns into Duffing equation. Because of $q<\text{1}$, the contribution of $q{w}^3$ term to the solution of the Eq. (24) is negligible near the equilibrium position, that allow to consider only the equation with quadratic nonlinearity instead of Eq. (21).

4. Conclusions

The system of dynamic equations of magnetoelasticity for rod is reduced to evolution equations with respect to the longitudinal deformation and intensity of the magnetic field, which are similar to known in nonlinear wave dynamics the Korteweg-de Vries equation and the Burgers equation but coupled together. As a result of analytical studies the possibility of the formation of intense periodic magnetoelastic waves and magnetoelastic solitons is demonstrated.