Noise subspaces subtraction in SVD based on the difference of variance values

1. Introduction

Noise is an inevitable phenomenon during signal acquisition. signals are polluted and the real working status are blurred in time and frequency domains because of noise. Therefore, denoising is a vital pre-processing step in signals processing.

Low-pass filter is a traditional denoising method but sometimes this filter is limited when a signal contains a sharp edge or an impulse in a short duration because these two kinds of drastic changes are not well caught. Moreover, this denoising method works on the basis that noise covers the high frequency band but the high frequency band of practical signals could also contain the useful components. In order to overcome the shortcomings of the traditional denoising method, some other methods are proposed such as wavelet thresholding and EMD denoising [1-5]. Wavelet thresholding conducts on the assumption that the signal magnitudes dominate the noise magnitudes, therefore the wavelet coefficients of noise can be set to zero when it is smaller than a preset thresholding value. However, the fixed basis function cannot guarantee a perfect match with real signals. Empirical Mode Decomposition(EMD) is a data-driven processing method which was introduced by Huang [6] in 1998 to analysis the non-stationary and non-linear signals. Afterwards EMD was improved by Wu Z. and Huang N. E. [7] by adding a group of Gaussian noise before decomposition and they called the improved method EEMD. EEMD overcomes mode aliasing to a great extent. EEMD is also be used to denoise signals [8-13]. Through EEMD a signal is decomposed to a series of Intrinsic Mode Functions (IMFs) and some of the IMFs belong to useful signal while some other IMFs belong to noise. The first kind of IMFs can be picked to reconstruct denoised signal, but some other problems such as end effect will affect the denoising performance.

Singular Value Decomposition (SVD) [14] is another data-driven signal processing method. When SVD is applied to denoising, firstly A one-dimensional signal can be rearranged to a signal matrix in Hankel matrix form. and then the signal matrix is decomposed to two unitary matrices and a diagonal matrix in which singular values are arranged in a descending order. Each dimension of the diagonal matrix is viewed as a subspace with a singular value in it. Considering that signal magnitude largely exceeds noise magnitude, subspaces with big singular values belong to signal subspaces while the other subspaces belong to noise subspaces. Therefore, a breaking point in singular values will exist. The traditional SVD denoising to determine the break point will be briefly explained in Part 3 [15]. This method is limited to deal with some periodic signal with a few impulses. Sometimes the breaking point is unobvious and different choices of different singular values will result in largely different reconstructed signals and a proper choice will result in a favorable reconstructed signal. However, little attention is put to the choice of proper singular values, researchers focus on the combination of the traditional SVD denoising and other denoising methods such as Savitzky-Golayz (SG) filter denoising and EMD denoising [16-20]. In this paper, an improved SVD denoising method based on the difference of variance values has an excellent performance by comparing with the traditional SVD denoising and other mainstream denoising methods such as wavelet thresholding and EEMD denoising.

2. Matrix construction and SVD algorithm

A polluted signal $x_n$ is a one-dimensional vector and its Hankel matrix ${\mathbf{H}}_n$ is constructed as Eq. (1):

In Eq. (1), $N$ is the length of $x_n$ and $1<n<N$.

There are many choices to form the Hankel matrices if $x_n$ has many data points. In order to make the Hankel matrix closer to a square matrix. The row number $m$ and column number $n$ are chosen in Eq. (2) and Eq. (3):

It is supposed that the signal $x_s$ is polluted by an additive white Gaussian noise $w_n$:

In Eq. (5) the ${\mathbf{H}}_n$, ${\mathbf{H}}_s$ and ${\mathbf{H}}_{wn}$ respectively denote the Hankel matrix of $x_n$, $x_s$ and $w_n$:

The SVD can be conducted because the Hankel matrices are real. The form of the decomposition is shown as Eq. (6):

In Eq. (6) ${\mathbf{H}}_n$ is a $m\times n$ matrix, $\mathbf{U}$ is a $m\times m$ orthogonal matrix, $\mathbf{S}$ is a $m\times n$ diagonal matrix and $\mathbf{V}$ is a $n\times n$ orthogonal matrix. $\mathbf{U}$ and $\mathbf{V}$ is respectively called left and right singular vectors. $\mathbf{S}$ can also be expressed as Eq. (7):

In Eq. (7) $\mathrm{\Sigma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_1,{\sigma }_2,\cdot \cdot \cdot ,{\sigma }_r)$ in which ${\sigma }_1>{\sigma }_2>\cdot \cdot \cdot >{\sigma }_r>0$.

Considering that signal magnitude exceeds noise magnitude and $\sigma$ are listed in a descending order, the singular values of signal lie in the front dimensions of $\mathrm{\Sigma }$. Suppose the front $s$ dimensions are signal subspaces. Eq. (6) can be transformed to Eq. (8). In Eq. (8) ${\mathrm{\Sigma }}_s$ and ${\mathrm{\Sigma }}_n$ respectively denote the singular values of the useful signal and noise:

Then:

Theoretically, there exists a breaking point which divides the two kinds singular values. After these values are separated. The clean signal can be achieved by reconstructing matrix ${\mathbf{H}}_s^{\text{'}}$:

3. Improved SVD denoising approach to subtract noise subspaces

Briefly, traditional SVD denoising involved eight major steps.

Step (1). Construct $x_n$’s Hankel matrix ${\mathbf{H}}_n$.

Step (2). Achieve ${\mathbf{U}}_n$, ${\mathbf{S}}_n$, ${\mathbf{V}}_n$ through SVD.

Step (3). Plot each singular value in ${\mathbf{S}}_n$ with respect to its column index.

Step (4). Find the breaking point in singular value-column plot.

Step (5). If the breaking point is unobvious in the plot, calculated difference values of the two successive singular values.

Step (6). Plot each difference value with respect to its column index and the index begins from 2.

Step (7). Find the top of the difference value-column plot and the top’s column index is the dimension where the breaking point is.

Step (8). Reconstruct denoised signal.

According to many experimental results, if more shocks and sharp edges exist in a signal, the relatively big singular values of the useful signal will distribute to a larger dimension. For example, $x_0$ is a linear signal and $x_1$ is a pulse signal. They are generated on the interval between $0$ and 1.024 with 0.001 step length. Both of them are polluted by an addictive Gaussian noise whose mean value is zero and standard deviation is 0.25 The time-domain plots of two polluted signals are shown in Fig. 1(a) and Fig. 2(a). According to Eq. (1). and Eq. (2), two 512×513 Hankel matrices are constructed. Through SVD Two diagonal matrices ${\mathbf{S}}_0$, ${\mathbf{S}}_1$ are achieved. Two groups of singular value-column plots and difference value-column plots are respectively drawn in a same plot which is shown in Fig. 1(b) and Fig. 2(b). Apparently, the distribution of $x_1$’s big singular values covers a larger dimension than $x_0$’s which correspond to aforesaid conclusion. Moreover, the breaking point of singular value curve in Fig. 1(b) is obvious and this point is also confirmed by the top of the difference value curve. However, the breaking point in singular value curve in Fig. 2(b) is not that obvious but we can find it by the top of the difference value curve. Therefore, the difference value can be used to find the breaking point more precisely.

Generally, Signals achieved in practice contain much less sharp edges than $x_1$, thus the big singular values of the useful signal cover only first few dozen dimensions of the matrix $\mathbf{S}$. In this paper the first 100 dimensions are chosen because these dimensions are enough to cover the breaking point. Specifically, we choose the first 1, 2,…, 99, 100 dimension of $\mathbf{S}$ respectively to reconstruct 100 analytical signals $x_{a1}$, $x_{a2}$,…, $x_{a99}$, $x_{a100}$.

Fig. 1x0 plots

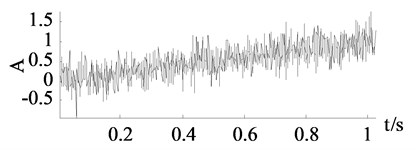
a)$x_0$ time-domain plot

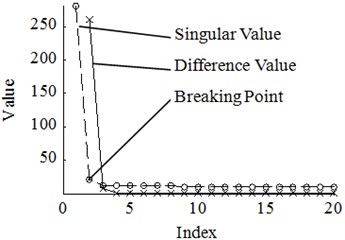
a)$x_0$ value-index plot

Fig. 2x1 plots

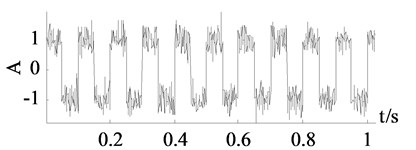
a)$x_1$ time-domain plot

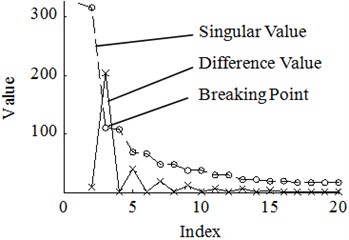
b)$x_1$ value-index plot

If a clean signal is polluted by an additive white Gaussian noise, the dispersion in time domain of the signal is much larger than the clean signal. Statistically, variance describes the dispersion of a series of points which is used is this paper. Variance is calculated by Eq. (11):

Through Eq. (11) 100 variances $s_1^2$, $s_2^2$,…, $s_{99}^2$, $s_{100}^2$ of the analytical signals are calculated. Because the breaking point divides the signal subspaces and noise subspaces, the noise composition of analytical signals will drastically change which will lead to a great change of $s^2$. Similarly, difference value is used to describe the change of $s^2$. ${\theta }_i$ is defined as the difference value of $s^2$. The point where $s^2$ drastically change is the point where ${\theta }_i$ meets its max value:

99 $\theta$ are calculated through Eq. (12). Find the index of the maximum of these $\theta$ and the index is the dimension where the breaking point is.

Briefly, the improved SVD denoising involves seven major steps.

Step (1). Construct $x_n$ Hankel matrix ${\mathbf{H}}_n$.

Step (2). Achieve ${\mathbf{U}}_n$, ${\mathbf{S}}_n$, ${\mathbf{V}}_n$ through SVD.

Step (3). Choose first 1, 2,…, 99, 100 dimension of ${\mathbf{S}}_n$ respectively to reconstruct 100 analytical signals $x_{a1}$, $x_{a2}$,…, $x_{a100}$.

Step (4). Calculate $s_1^2$, $s_2^2$,…, $s_{99}^2$, $s_{100}^2$ of the analytical signals.

Step (5). Calculate ${\theta }_1$, ${\theta }_2$,…, ${\theta }_{98}$, ${\theta }_{99}$.

Step (6). Find the maximum ${\theta }_{imax}$ of ${\theta }_i$.

Step (7). $x_{aimax}$ is the final denoised signal.

4. Numerical experiments

Four signals are generated on the interval between $0$ and 1.024 with 0.001 step length:

$x_4$ is a chirp signal whose frequency is 10 at zero and 30 at the point of 1024.

$x_5$ is one period of ECG signals.

Periodic vibration is a universal vibration form. Therefore, periodic signals $x_2$ and $x_3$ are simulated. $x_2$ has an invariable amplitude while $x_2$ has an degenerative amplitude. $x_3$ frequency changes constantly while its amplitude remains invariable. Additionally, $x_5$ is the most commonly used aperiodic signal and also it is used in this paper to evaluated the denoising performance of the improved SVD denoising.

These four signals are all polluted by an addictive Gaussian noise whose mean value is zero and standard deviation is 0.25. Other two mainstream denoising methods wavelet thresholding and EEMD denoising are compared in this paper. the clean signals, polluted signals, denoising signals denoised by the traditional SVD denoising, wavelet thresholding, EEMD denoising and the improved SVD denoising are respectively shown in Fig. 3, Fig. 4, Fig. 5 and Fig. 6.

Fig. 3Signals of x1

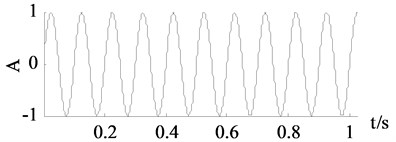
a) Clean signal

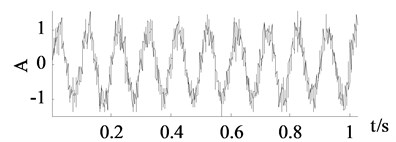
b) Polluted signal

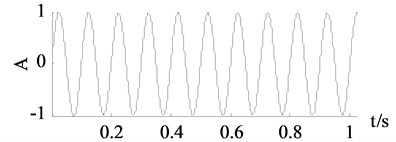
c) Traditional SVD denoising

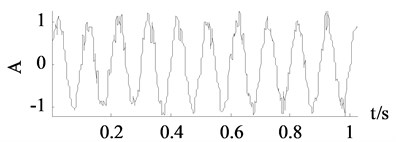
d) Wavelet thresholding

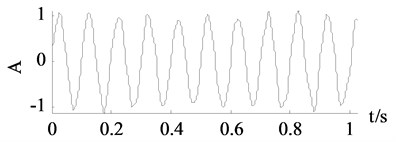
e) EEMD denoising

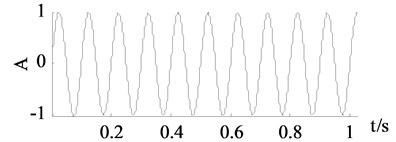
f) Improved SVD denoising

It can be seen from Fig. 3 and Fig. 4 that the traditional SVD denoising and the improved SVD denoising have a same denoising effect. It is also confirmed by the experimental results that both of the methods choose the first two dimensions as useful signal subspaces. Noise are largely eliminated by the traditional SVD denoising and the improved SVD denoising. However, the other two groups of curves achieved by wavelet thresholding and EEMD denoising are less close to the clean signals.

It can be seen from Fig. 5, the curves achieved by wavelet thresholding, EEMD denoising and improved SVD denoising method are close to the clean signal. The change of the frequency is well caught and the amplitude is relatively steady. In numerical experiment the improved SVD denoising choose the first 16 dimensions while the traditional SVD denoising chose the first 10 dimensions thus some components missed after reconstruction. Therefore, the curve in Fig. 5(c) is anamorphic.

Fig. 4Signals of x2

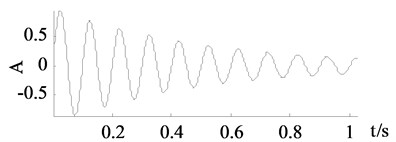
a) Clean signal

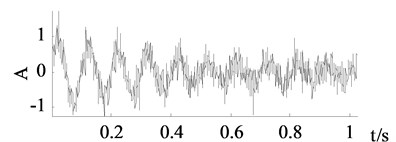
b) Polluted signal

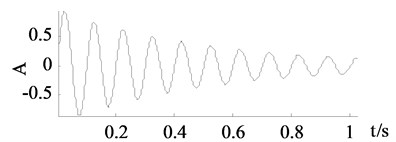
c) Traditional SVD denoising

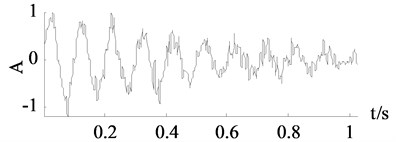
d) Wavelet thresholding

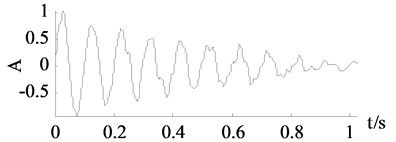
e) EEMD denoising

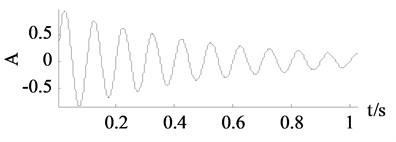
f) Improved SVD denoising

Fig. 5Signals of x3

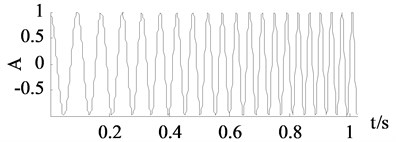
a) Clean signal

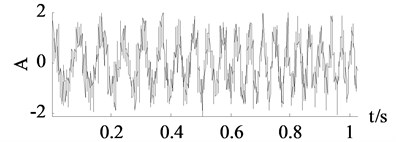
b) Polluted signal

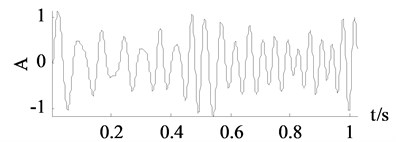
c) Traditional SVD denoising

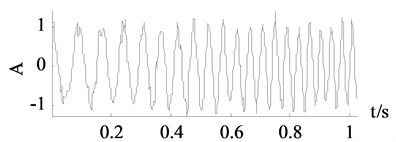
d) Wavelet thresholding

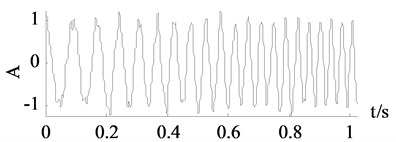
e) EEMD denoising

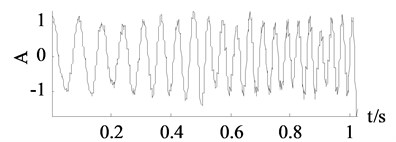
f) Improved SVD denoising

From Fig. 6, the curves achieved by wavelet thresholding, EEMD denoising and improved SVD denoising are also close to the clean signal. Some important turning points and sharp edges are caught. In numerical experiment the improved SVD denoising chose the first 12 singular values while the traditional SVD denoising chose the first 6 singular values thus a lot of important components missed which results a totally different denoised curve in Fig. 6(c).

Fig. 6Signals of x2

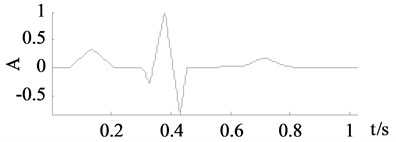
a) Clean signal

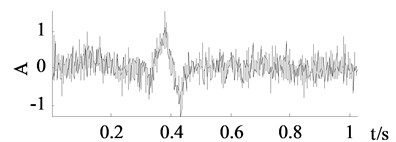
b) Polluted signal

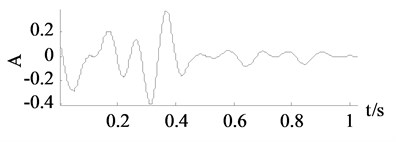
c) Traditional SVD denoising

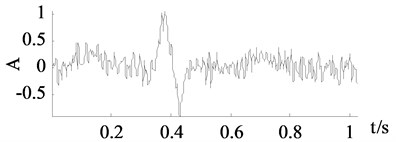
d) Wavelet thresholding

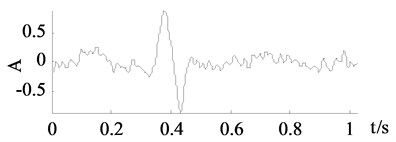
e) EEMD denoising

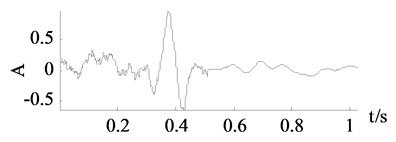
f) Improved SVD denoising

The parameters Signal Noise Ratio (SNR) and Mean Absolute Error (MAE) are widely used to evaluate the performance of denoising [8]. The final denoising performance of SNR and MAE are listed in Table 1 In which the most optimal parameters are bold.

Form Table 1, three conclusions are achieved.

I. Noise is harder to be eliminated in aperiodic signals than in periodic signals because the SNRs of aperiodic signals in generally are smaller than periodic signals while the MAEs are bigger.

II. The traditional SVD denoising and the improved SVD denoising have a better ability of processing periodic signals than EEMD denoising and wavelet thresholding. The final SNRs and MAEs of $x_1$ and $x_2$ are same because the same singular values are chosen.

III. From periodic signals to aperiodic signals, the regularity of the chosen signals is decreasing. The improved SVD denoising method gains an edge over other three methods especially when processing the ECG signal because SNRs and MAEs exceed other methods. Therefore, the improved SVD denoising can be judged to have a favorable ability to process aperiodic signals.

5. Hydraulic signal denoising

A hydraulic signal is used to evaluate the denoising performance of the improved SVD denoising method proposed in the paper, the signal is texted in a hydraulic complex test-bed. The test-bed and the data-acquisition device are shown in Fig. 7. In Fig. 7(b), on the operation panel there are different valves meant to realize different working status. Valve A is meant to realize the leakage status, valve B is a speed control valve, valve C is meant to realize cavitation status and valve D is meant to realize blocking status. In Fig. 7(c), the data-acquisition software acquires data through displacement sensors which can be absorbed on measured objects tightly by magnetic force.

Fig. 7Figures of text-bed and data acquisition device

a) Overall figure of test-bed

b) Valves distribution

c) Data-acquisition device

$x_6$ is a signal of 1024 points subtracted form a long signal achieved in an integrated hydraulic test stand. The signal is denoised by the improved SVD denoising. In order to make the curves easily identified, only the first 100 data points are chosen to be plotted. The time-domain plot of the original signal and the denoised signal are shown in Fig. 8.

Fig. 8Signals of x6

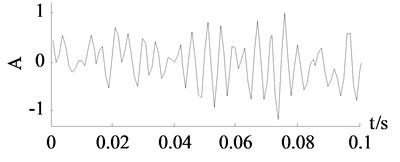
a) Original signal

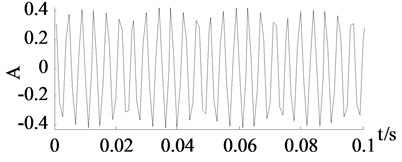
b) Denoised signal

From the curve in Fig. 8, the periodicity of the denoised signal can be easily identified. Although the denoising performance of tested signals cannot be evaluated by SNR and MAE, the feature of the original signal is more obvious after denoising. It is enough to conclude that the improved SVD denoising is of practical use.

6. Conclusions

This paper improved the traditional SVD denoising which is merely good at processing periodic signals. While the improved SVD denoising based on the difference of variance value further extends SVD denoising to aperiodic signals and receives a good effect by comparing with other mainstream denoising methods. Considering that aperiodic signals are more common in actual occasions, the improved SVD denoising has some application prospect. The important step of SVD denoising is noise subspace subtraction. This step is based on the assumption that each subspace only contains useful signals or noise. Sometimes especially in the high-frequency band noise and useful signal will co-exist. Our further work will focus on the removal of the noise in each subspace.