A new rockfill dynamic characteristics analogy method using statistic relationship

1. Introduction

On May 12, 2008, an earthquake of magnitude 8.0 occurred in Wenchuan, which is located in Sichuan Province, China. After the earthquake, 2,666 dams in eight provinces suffered different extents of damage [1]. On July 11, 2008, the Chinese government announced that certain dams, which satisfy one of the conditions listed in Table 1, that have been built or that are under construction undergo special seismic design censorship, which is primarily dependent on dynamic analysis with the finite element method (FEM). Before the Wenchuan earthquake, only a few large dams satisfying the conditions mandated by the Chinese Specifications for Seismic Design of Hydraulic Structures should take dynamical analysis with the FEM. As new conditions listed in Table 1 are more comprehensive, numerous middle-scale dams should use dynamic analysis with the FEM to analyze the seismic safety of the dam. In July 2010, the government launched reinforcement work for unsafe small-scale reservoirs; approximately 5,400 unsafe small-scale dams required reinforcement design according to the results of seismic dynamic analysis by the FEM.

The dynamic characteristics of the soil in earth-rockfill dams (generally acquired by dynamic tests, such as dynamic triaxial tests, dynamic simple shear tests, cyclic torsional shear tests, resonant column tests, and shear wave velocity tests) determine the results of the FEM analysis. Due to high costs, long periods, and limited service, dynamic tests have only been conducted for some of the dams. The dynamic characteristics of soil for the majority of small- to middle-scale dams are determined by the analogy method which refers to using or making adjustment to the similar soil dynamic characteristics as the analogized soil dynamic characteristics, according to the soil parameters such as material, dry density, grading curve, and so on. It is highly dependent on personal experience and lacks objective and accurate orientations. A simple, reliable, and effective method to analogize soil dynamic characteristics should be developed for small- to middle-scale dams using dynamic FEM analysis.

The dynamic characteristics of soil in earth-rockfill dams can be generally described by an equivalent linear viscoelastic model, which incorporates the initial dynamic elastic shear modulus $G_{max}$, normalized modulus reduction relationships $G/G_{max}~\gamma$ ($G$ is dynamic shear modulus and $\gamma$is dynamic shear strain), and the damping ratio $\xi$ versus $\gamma$ relationships $\xi ~\gamma$. $G_{max}$ can be obtained at small-strain cyclic loading ($\gamma$ is typically less than 0.001 %), when the soil is in an elastic state. Numerous scholars have performed experiments to examine $G_{max}$, which is a key factor in soil dynamic characteristics[2,3]. $G/G_{max}~\gamma$ and $\xi ~\gamma$ are also important factors. Seed et al. developed ranges of $G/G_{max}~\gamma$ and $\xi ~\gamma$ for sandy and gravelly soils [3]. Rollins et al. provided best-fit curves and standard deviation bounds of $G/G_{max}~\gamma \mathrm{}$and $\xi ~\gamma$ for gravel [4]. Kong et al. proposed ranges of $G/G_{max}~\gamma$ and $\xi ~\gamma$ for rockfill [5]. The author developed $G/G_{max}~\gamma$and $\xi ~\gamma$ statistic curves for rockfill, which were applied in the dynamic analysis of two middle-scale CFRDs. The details were published in the 15th World Conference on Earthquake Engineering (15WCEE).

In this paper, a statistical relationship between $G_{max}$ and Duncan and Chang’s $E$-$B$ model parameters $E_0$ of rockfill was developed. According to prototype monitoring of a dam, $E_0$ of the rockfill were determined by a back analysis, which reflected the influence of construction. The $G_{max}$of rockfill can be analogized according to the statistical relationship and $E_0$. According to the analogized $G_{max}$, $G/G_{max}~\gamma$ and $\xi ~\gamma$ statistic curves of the rockfill, the $G/G_{max}~\gamma$ and $\xi ~\gamma$curves were analogized.

2. The analogy method of ${\mathit{G}}_{\mathit{m}\mathit{a}\mathit{x}}$

The $G_{max}$ of soil is affected by many factors, such as particle size, material, gradation, confining pressure, fabric of soil skeleton, stress path, loading frequency, density, saturation, and temperature [2]. Different soils are affected by different factors. Thus, the $G_{max}$ of clays, slits, sands, gravel soils, and rockfills should be described differently.

Seed et al. developed the empirical function of granular soils (sand and gravels) as:

where $K_2$ is a shear modulus coefficient, which can be determined by the standard penetration test,$\mathrm{}{\sigma }_0^{\mathrm{\text{'}}}$ is the mean effective confining pressure, $P_a$ is the atmosphere [3].

Hardin and Kalinski modified the $G_{max}$ empirical function of sand to estimate the $G_{max}$ of gravelly soils as:

where $G_{ij}^e$ is the elastic shear modulus in three-dimensional formats, $e$ is the void ratio, $OCR$ is the over consolidation ratio, $S_{ij}$ is the dimensionless elastic stiffness coefficient, ${\sigma }_{ii}^{\mathrm{\text{'}}}$ is the principle stress, $v^e$ is the elastic Poisson’s ratio, $f\left(D\right)$ is the particle size function, and $k$ and $n$ are model parameters [6].

These empirical functions provided a practical method for determining the $G_{max}$ of sand and gravel that corresponds to filter material and transition material in earth-rockfill dams. However, compared with the soils mentioned above, less effort has been applied to the $G_{max}$ empirical function of rockfill. Rockfill, which is typically the largest component of an earth-rockfill dam, primarily affects the displacement of such dams. Furthermore, the $G_{max}$ of rockfill measured in the laboratory using the maximum particle sizes in the samples are less than 60 mm. However, the maximum particle sizes of the rockfill in earth-rockfill dams may be as large as 1 m. The particle size affects the rockfill deformation properties. The rockfill shear deformation modulus increases as the particle sizes become larger for a given sample diameter and increases with the sample diameter for a given particle gradation [7]. Moreover, rockfill is produced by quarry blasting, the particles contain a few cracks, which result in considerable particle breakage. Particle breakage, which can be depicted by gradation curves, contributes to modified soil skeleton structures and affects the deformation characteristics of rockfill. Thus, the deformation characteristics of rockfill are influenced by compaction on a construction situ. The results of numerical simulation with the FEM in laboratory tests sometimes differ significantly from the results of prototype monitoring.

As noted previously, the $G_{max}$ empirical function for rockfill does not incorporate the influences of particle size and construction on the site. Back analysis, which yields a more accurate numerical simulation, can be applied to determine the deformation characteristics of soil in dams. However, a complete seismic wave and corresponding seismic response of earth-rockfill were rarely collected, with the exception of a few earth-rockfill dams, such as the Li-yu-tan Dam, which was damaged but not completely destroyed by the Chi-Chi earthquake [8]. Dynamic back analysis of earth-rockfill is more difficult, and the dynamic characteristics of soils in dams are difficult to determine directly by dynamic back analysis. Conversely, the static back analysis method is widely applied. Complete deformation prototype monitoring of earth-rockfill dams is the predominant method for monitoring dam security. Static soil deformation characteristics determined by back analysis with prototype monitoring reflect the influences of construction and particle size, and provide more reliable evidence for $G_{max}$ analogy.

The Duncan and Chang’s $E$-$B$ model is a simple and practical nonlinear elastic static model. It is recommended by Chinese Design specification for rolled earth-rockfill dams (DL-5395-2007) to calculate displacement and stress of earth-rockfill dam. The Chinese Specification of soil test (SL237-1999) also provides techniques, which are used to determine soil parameters used in the Duncan and Chang’s $E$-$B$ model according to triaxial test results. The Chinese engineering practices indicate that the Duncan and Chang’s $E$-$B$ model can well simulate the settlements of earth-rockfill dams, whose computational accuracy satisfies the demand for engineering.

The Duncan and Chang’s $E$-$B$ model suggested that the tangent modulus $E_t$ is expressed as follows:

where $R_f$ is the failure ratio, $S$ is the stress level, $K_e$ is the modulus number, ${\sigma }_3$ is the minor principal stress, $n_e$ is the modulus exponent, ${\sigma }_1$ is the major principal stress, $\phi$ is the friction angle, and $c$ is the cohesion.

The nonlinear volume change is simulated using the bulk modulus, which is expressed as follows:

where $K_b$ is the bulk modulus number and $m$ is the bulk modulus exponent.

The Mohr-Coulomb envelopes for cohesionless soils are curved to some extent, and a wider range of pressure corresponds to a greater curvature, particularly for gravel and rockfill. For example, at the bottom near the center of a large dam, the rockfill may be confined under such a large pressure that the friction angle is:

where ${\phi }_0$ is the value of $\phi$ for ${\sigma }_3=P_a$, and $\mathrm{\Delta }\phi$ is the reduction in $\phi$ for a 10-fold increase in ${\sigma }_3$ [9]. Thus, $\phi$ and $c$ in Eq. (3) should be replaced by ${\phi }_0$ and $\mathrm{\Delta }\phi$, respectively, for rockfill materials.

In the equivalent linear viscoelastic model, $G_{max}$ can be expressed as:

where $K_g$ is the dimensionless elastic stiffness coefficient and $n_g$ is the elastic stiffness exponent. Although the $E_0$ in Eqs. (4) and (6) are similar because they both indicate the influence of stress on the deformation behavior of the soil, some differences remain. First, $G_{max}$ is the secant modulus of the dynamic shear stress versus shear strain curves, whereas $E_0$ is the tangent modulus of the static shear stress versus axial strain curves. Second, $G_{max}$ and $E_0$ are both determined by a modified straight-line function; the dynamic shear strain in the x-axial of $G_{max}$ begins at 10^-6, whereas the static axial strain in the $x$-axial of $E_0$ begins at 10^-3. Third, $G_{max}$ is determined in the undrained condition; thus, the volumetric strain cannot be tested; Poisson’s ratio was generally estimated at 0.5 [4, 5]. Conversely, $E_0$ is determined in the drained condition. Finally, ${\sigma }_0^{\mathrm{\text{'}}}$ in the $G_{max}$ function incorporates the influence of the consolidation ratio and is equivalent to ${\sigma }_3$ in the $E_0$ function when the consolidation ratio is equivalent to one. However, $G_{max}$ and $E_0$ both represent elastic shear modulus and contain the same units. They are both expressed by the stress function, which indicates the pressure hardening characteristics of the soil. Furthermore, $E_0$ is the most important parameter in the $E$-$B$ model that simulates deformation of the soil, which directly reflects the influence of construction on the displacement of an earth-rockfill dam.

So it is would be an effective method to develop an empirical relationship between $E_0$ and $G_{max}$ according to static and dynamic test results of the rockfill, which is similar to methods used to resolve $G/G_{max}~\gamma$ and $\xi ~\gamma$. According to the empirical relationship between $E_0$ and $G_{max}$, the $G_{max}$ can be analogized using $E_0$, which avoids the dynamic test. The author compiled the $G_{max}$ and $E_0$ parameters of 33 types of rockfill that are used in 14 earth-rockfill dams, as listed in Table 3. According to the compiled reference, these parameters are all obtained by the laboratory test, whose details are listed in Table 2.

Fig. 1Best-fit curve, the Best-fit curve ± one and two SD, and data points that define Kg/Ke versus Ke relationships for 33 types of rockfills

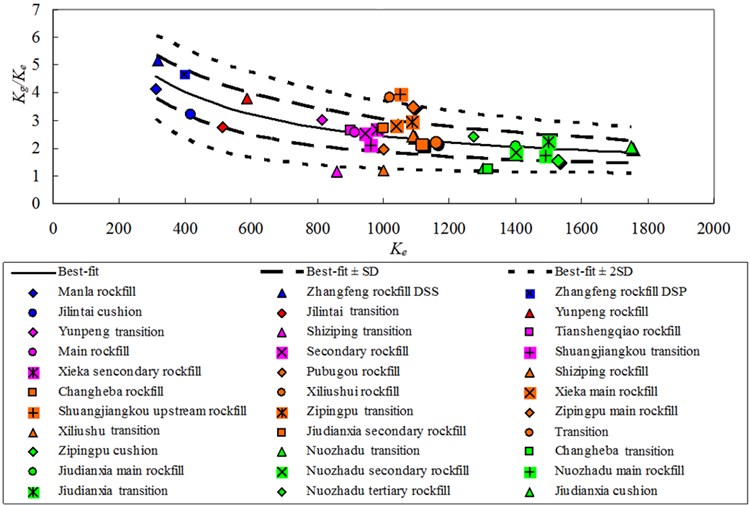
Fig. 2Best-fit curve, the Best-fit curve ± one and two SD, and data points that define ng/ne versus ne relationships for 33 types of rockfills

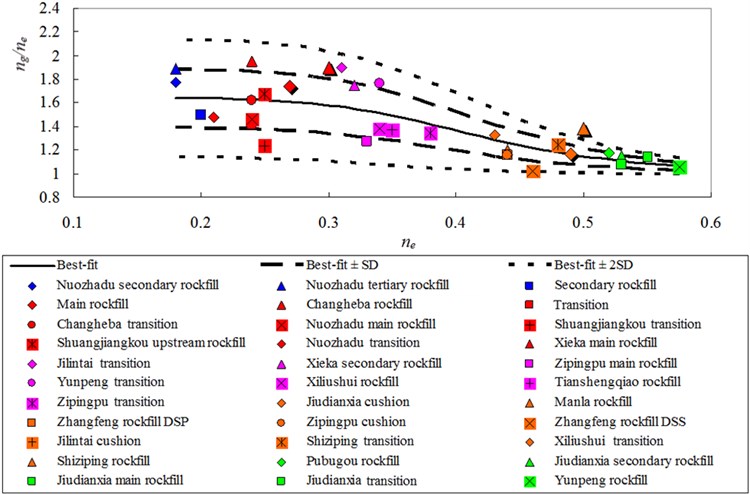
The $K_g/K_e$ versus $K_e$ data points for the rockfills listed in Table 3 are plotted in Fig. 1, and $n_g/n_e$ versus $n_e$ data points are plotted in Fig. 2. The $K_e$ and $K_g$ represent the influences of material stiffness and soil skeleton structure on $E_0$ and $G_{max}$, respectively, whereas $n_e$ and $n_g$ reflect the sensitivity of soil skeleton structure to stress. As mentioned previously, $K_g$ and $n_g$ are typically acquired in an anisotropic consolidation state, whereas $K_e$ and $n_e$ are acquired in an isotropic consolidation state. This difference is eliminated by ${\sigma }_0^{\mathrm{\text{'}}}$ , which is equivalent to ${\sigma }_3$ when the consolidate ratio is equivalent to one. Thus, $K_g$ and $K_e$ are equivalent, and $n_g$ and $n_e$ are equivalent. Figs. 1 and 2 highlight that $K_g/K_e$ decreases as $K_e$ increases, and $n_g/n_e$ decreases as $n_e$ increases. The data points in Fig. 2 are more concentrated than the data points in Fig. 1, whereas $n_g$ is more concentrated than $K_g$. The $n_g$ values for the 33 types of rockfills are distributed over the range of 0.3–0.7. The results are slightly more comprehensive than the previous statistical results obtained by Professor Kong for 13 types of rockfills, which fall in the range of 0.4-0.6 [5]. The average value of $n_g$ is 0.5, as indicated by the results of Professor Kong [5]. The $n_e$ distribution falls in the range of 0.2-0.6, and higher $n_e$ values typically correspond to higher $n_g$ values. Thus, $n_g/n_e$values are distributed over the range of 1.0-2.2 and are concentrated in a smaller range with an increasing $n_g$. Conversely, the distribution of $K_g/K_e$ values is slightly affected by the $K_g$ values.

The equations for the best-fit curves of the date in Fig. 1 and Fig. 2 are:

where $a_1$, $b_1$, $m_1$, $B_1$, and $B_2$ are the fitting parameters. The best-fit curve and the best-fit curve ± one and two standard deviations (SD) are also shown in Figs. 1 and 2. The fitting parameters are listed in Table 4.

The scatter of the data is difficult to resolve by the existing analysis because particle material, particle gradation, density, and soil skeleton structure may influence $K_g$ and $K_e$. The $K_e$ and $n_e$ of rockfill used in dams can be determined according to the triaxial tests or the back-analysis using the prototype monitoring. The $K_g$ and $n_g$can be determined by Eq. (7) with the best-fit curve, and sensitivity analysis can be applied with the best-fit curve ± one and two SD. Thus, $G_{max}$ can be analogized according to the developed statistical relationship, which avoids the dynamic test. Furthermore, the analogized $G_{max}$ would reflect the influence of the construction in situ, if the $K_e$ and $n_e$ are determined by the back-analysis using the prototype monitoring.

3. The analogy method of ${\mathit{G}}_{\mathit{m}\mathit{a}\mathit{x}}~\mathit{\gamma }$ and $\mathit{\xi }~\mathit{\gamma }$

In the past several decades, many researchers have explored ${G/G}_{max}~\gamma$ and $\xi ~\gamma$ of soil and have developed the ranges of shear moduli and damping ratios for cohesive soil, sand, gravel, and rockfill [3-5]. The author gathered dynamic characteristics of numerous rockfills in earth-rockfill dams both in China and abroad, developed ${G/G}_{max}~\gamma$ and $\xi ~\gamma$ statistic curves for rockfill, and applied them in the dynamic analysis of two small- to middle-scale CFRDs. The details are presented in the paper “Application of rockfill dynamical characteristic statistic curve in mid-small scale concrete face dam dynamic analysis”, which was published in the 15WCEE. The statistic curves of and can be expressed as:

where $b$ is minimum ${G/G}_{max}$ versus $\gamma$ between 10^-6-10^-1; $A_1$ and $A_2$ are maximum $\xi$ and minimum $\xi$, respectively, versus $\gamma$ between 10^-6 and 10^-1; and $x_0$, $m$, $a$, and $n$ are fitting parameters. The parameters are presented in Table 5.

Thus, the dynamic characteristics of the rockfill used in the dam can be determined; $G_{max}$ can be analogized according to $E_0$ and $G_{max}$ statistic curves; and ${G/G}_{max}~\gamma$ and $\xi ~\gamma$ can be analogized by the statistic curves. To examine the effectiveness, this study applied the dynamic analysis of a middle-scale CFRD whose rockfill dynamic parameters were analogized according to the proposed method.

4. Application

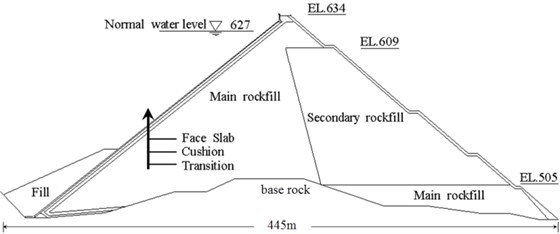
The Malutang II CFRD is located along the Panlong River in the Yunnan province of China. Along the crest, the dam is 154 m high and 493.4 m long; the upstream dam slope is 1:1.4, and the downstream integrated dam slope is 1:1.3. The total reservoir capacity is 5.36×10⁸ m³, and the install capacity is 300 MW. The design intensity of the Malutang II is 7.0 degree. So according to conditions of the specifications listed in Table 1, the Malutang II degsign intensity equal 7.0 degree, and the reservoir is less than 10⁹ m³, and the install capacity is less than 1,200 MW, which don’t need to take dynamical analysis with the FEM. However, according to the new order, the Malutang II reservoir is more than 10⁸ m³, and the install capacity is larger than 300 MW, which should take dynamical analysis with the FEM. A typical section of the CFRD is provided in Fig. 3.

Fig. 3Typical section of the Malutang II CFRD at 0+233.159

4.1. ${\mathit{E}}_0$ back analysis according to prototype monitoring

The three-dimensional FE mesh of Malutang II is shown in Fig. 4. The three-dimensional FE mesh is composed of 8,284 elements. The rockfills, cushion, transition, and concrete face slabs were simulated by four-, six-, and eight-node isoparametric spatial elements. A detailed settlement monitoring system was established to monitor the deformation of the Malutang II CFRD [24]. Vertical displacements inside the dam body were measured by settlement gauges distributed throughout typical cross-sections at 0+233.159. Twenty-two hydraulic overflow settlement gauges along three monitoring lines were placed in the typical sections, of which 19 survived (at elevations of 522, 556, and 590 m). Two other monitoring gauges, for monitoring settlement and horizontal displacement, were distributed on the downstream slope of the typical section at elevations 565 and 595 m. The layout of displacement gauges in the typical section is presented in Fig. 5.

Fig. 4Three-dimensional FE mesh

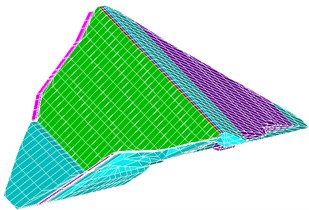
Fig. 5Comparison of simulations and site measurements

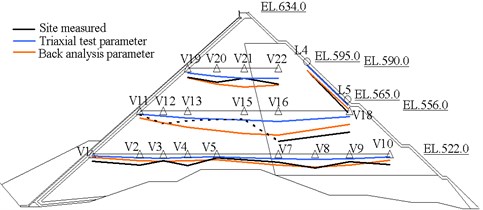
The site-measured displacements and construction record indicated that rapid construction reduced the time of consolidation [24], modified the structure of the rockfill, and caused the rockfill density to be unevenly distributed. The uneven density of the rockfill affected the rockfill deformation modulus and the dam body displacement. According to the construction record, the main rockfill and the secondary rockfill were separated into three parts corresponding to the three construction rates. Thus, the main rockfill types I, II, and III represent the main rockfill types that are constructed in stages I, II, and III & IV, respectively. The same notation is applied for secondary rockfill. The fill zone material was simulated using secondary rockfill II in the back-analysis. Therefore, Duncan and Chang’s $E$-$B$ model parameters $K_e$, $n_e$, $R_f$, ${\phi }_0$, $\mathrm{\Delta }\phi$, $K_b$, and $m$ of the main rockfill and the secondary rockfill in these construction periods were back-analyzed. The details of the $E$-$B$ model parameters back-analysis are listed in the reference [24]. The results of the back-analysis are shown in Table 6. The FEM analysis was conducted using model parameters obtained from the back-analysis. The displacements calculated from the back-analysis parameters are also shown in Fig. 5. The settlements calculated using the back-analysis parameters are consistent in magnitude and distribution with the values measured in situ. Therefore, in general, the back-analysis results satisfactorily reflect the deformation properties of the dam.

Table 6The back-analyzed E-B parameters of Malutang rockfill [24]

Methodology	Material	$K_e$	$n_e$	$R_f$	${\phi }_0$	$\mathrm{\Delta }\phi$	$K_b$	$m$
Triaxial test	Main rockfill	1,467	0.38	0.80	55.0	15.0	1,570	0.23
	Secondary rockfill	1,042	0.53	0.75	50.7	10.5	933	0.08
	Cushion	1,963	0.35	0.74	55.5	13.2	1,742	0.21
	Transition	1,583	0.35	0.74	57.6	16.5	1,590	0.16
	Fill	1,042	0.53	0.75	50.7	10.5	933	0.08
Back-analysis	Main rockfill I	1,011	0.33	0.90	55.0	16.0	1,112	0.22
	Main rockfill II	712	0.40	0.85			422	0.45
	Main rockfill III	1,545	0.18	0.60			1,663	0.47
	Secondary rockfill I	901	0.22	0.62	50.0	5.0	517	0.15
	Secondary rockfill II	311	0.20	0.90			207	0.05
	Secondary rockfill III	1,200	0.31	0.60			558	0.32

4.2. Analogy of the dynamic characteristics

In the dynamic analysis, an equivalent nonlinear viscoelastic model was employed. In this model, the dynamic shear modulus and damping ratio are calculated as:

9

$\frac{G}{G_{max}}=\frac{1}{1+k_1\gamma },\xi ={\xi }_{max}\frac{k_1\overline{\gamma }}{1+k_1\overline{\gamma }},\overline{\gamma }=\frac{\gamma }{{({\sigma }_0^{\text{'}}/P_a)}^{1-n_g}},G_{max}=K_g{P}_a{\left(\frac{{\sigma }_0^{\text{'}}}{P_a}\right)}^{n_g},$

where $\overline{\gamma }$ is the normalized shear strain and $k_1$ and ${\xi }_{max}$ are the model parameters. The parameters $K_g$ and $n_g$ are determined by Eq. (7) according to the best-fit curve and the $E$-$B$ model parameters determined by back analysis in Table 6. The analogized $G/G_{max}~\gamma$ and $\xi ~\gamma$ curves of the rockfill are plotted in Figs. 6 and 7.

The normalized shear strain $\overline{\gamma }$ reflects the influence of the mean effective stress on the damping ratio. The $\xi ~\gamma$curves with mean effective stresses of 100 and 1,600 kPa are plotted in Fig. 7. The $G/G_{max}~\gamma$ and $\xi ~\gamma$ curves of the soil reflect the energy transformation mechanism under dynamic loading. Higher soil skeletal stiffness can store more elastic energy and produce a smaller damping ratio, which is the ratio between the lost energy and stored energy. However, the rockfill structure is more complex, and many factors influence energy transformation. Friction among soil particles, pore-fluid flow, and particle breakage consume energy generated by dynamic loading. Denser rockfill produces a stronger soil skeleton and higher $G$.

Fig. 6Analogized G/Gmax~γ of the rockfill in the Malutang II CFRD

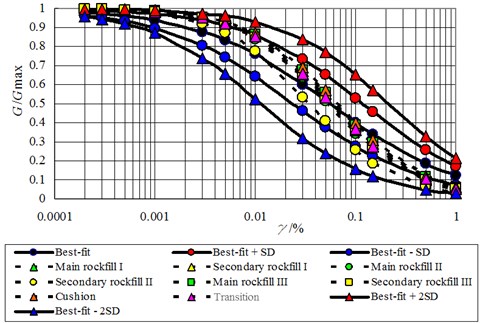
Fig. 7Analogized ξ~γ of the rockfill in the Malutang II CFRD

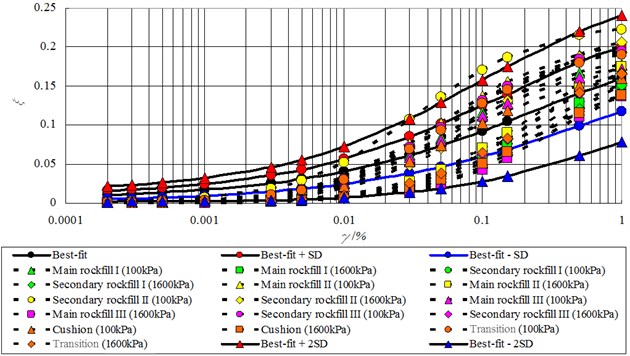
However, denser rockfill also generates additional particle contacts, greater dissipated energy, and a higher damping ratio [3]. The $E$-$B$ model parameters for the rockfill determined by back analysis indicated that small $K_e$ values generate high $n_e$ values. A small $K_e$ indicated that the soil exhibited a looser structure or contained softer particles. A large $n_e$ indicated that the soil exhibited a flexible skeleton and sensitivity to stress [25]. The site monitoring and back analysis results indicated that different densities significantly influenced the deformation modulus of the rockfill. Denser rockfill produced higher $G$ and $\xi$ values [3]. The analogized $G_{max}$ parameters $K_g$ and $n_g$ also conformed to the rules. Thus, the analogized curves with a mean effective stress of 100 kPa, as shown in Fig. 7, are all located above the best-fit curve even if the analogized $K_g$ is higher than the average values of the compiled rockfill. The largest damping ratio of the secondary rockfill II is maintained under the best-fit curve + 2 SD because the analogized $K_g$ is larger than the smallest value for the compiled rockfill. In this context, a higher $G_{max}$ produces a lower $\xi ~\gamma$ curve and a higher ${G/G}_{max}~\gamma$ curve, which conform to the general rules. The analogized dynamic parameters are listed in Table 7.

Table 7The analogized dynamic parameters

Material	$K_e$	$k_1$	$n_g$	${\xi }_{max}$
Main rockfill I	2,445	16.3	0.51	0.188
Main rockfill II	2,083	19.0	0.55	0.210
Main rockfill III	3,022	15.8	0.30	0.182
Secondary rockfill I	2,317	17.6	0.36	0.203
Secondary rockfill II	1,426	29.0	0.33	0.230
Secondary rockfill III	2,655	18.0	0.49	0.202
Cushion	3,053	15.0	0.54	0.171
Transition	2,371	17.4	0.53	0.201
Fill	2,280	18.0	0.49	0.205

4.4. Dynamic response of the dam

The earthquake time-step in the calculations was 0.02 s, and the acceleration in the vertical direction was reduced to two thirds. The acceleration responses of the Malutang II CFRD are presented in Fig. 9. The acceleration responses demonstrate that the maximum accelerations of the two earthquakes in every direction are located on the top of the dam. The maximum accelerations of the design earthquake in the upstream-downstream direction, vertical direction, and dam axis direction are 0.235, 0.137, and 0.173 g, respectively. The acceleration amplifications are 4.70, 4.11, and 3.46. The values of the check earthquake are 0.275, 0.187, and 0.189 g. The acceleration amplifications are 2.89, 2.96, and 1.99. The dynamic FEM results indicate that the maximum accelerations of the dam increase with the maximum accelerations of the earthquake and that the acceleration amplifications decrease with the maximum accelerations of the earthquake, which correspond to the earthquake response and the dynamic FEM analysis response of the same type of CFRD [17, 20-22, 28, 29].

Fig. 8Earthquake wave of the Malutang II CFRD

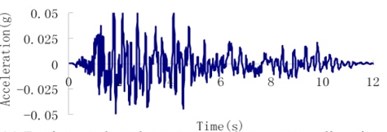
a) Design earthquake upstream-downstream direction

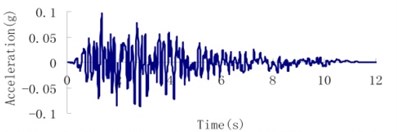
d) Check earthquake upstream-downstream direction

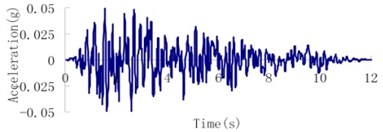
b) Design earthquake vertical direction

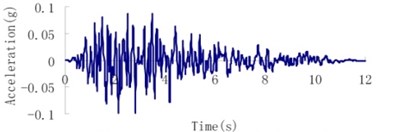
e) Check earthquake vertical direction

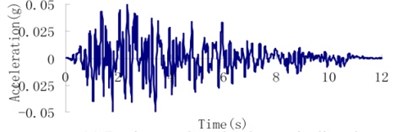
c) Design earthquake dam axis direction

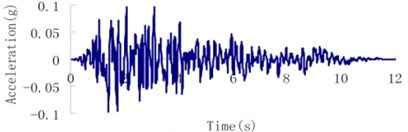
f) Check earthquake dam axis direction

Fig. 9Acceleration of the Malutang II CFRD

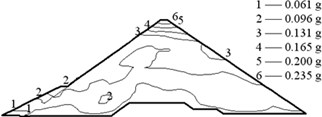
a) Design earthquake upstream-downstream direction

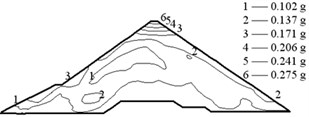
d) Check earthquake upstream-downstream direction

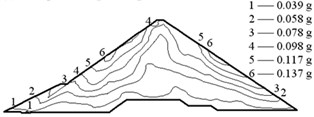
b) Design earthquake vertical direction

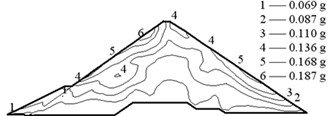
e) Check earthquake vertical direction

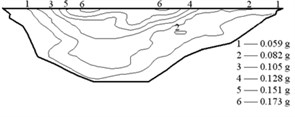
c) Design earthquake dam axis direction

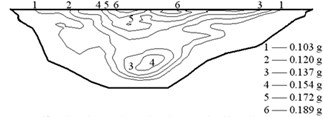
f) Check earthquake dam axis direction

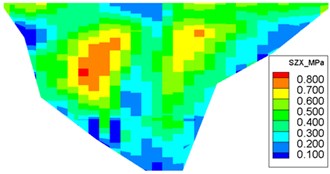
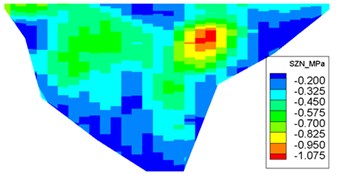
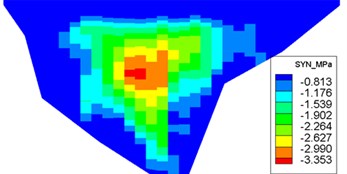
The dynamic stresses on the concrete face-slab of the design and check earthquakes are presented in Figs. 10 and 11, respectively. The maximum face-slab dynamic stresses of the design and check earthquakes are both located in the middle area. The maximum dynamic compression and tensile stresses along the dam slope for the design earthquake are 2.695 and 2.958 MPa (compression is positive). The stresses along the dam axis are 0.8 and 1.075 MPa. Check earthquake stresses along the dam slope are 4.369 and 3.353 MPa. The stresses along the dam axis are 1.558 and 1.644 MPa. The slab dynamic stresses increase with the maximum acceleration of the earthquake. The maximum compression stress and tensile stress are nearly equivalent; the stress along the dam slope is larger than the stress in the dam-axis direction, because the slit joints among face slabs release the part of the dynamic deformation in the face slab along the dam axis. As indicated by the acceleration response and distribution of the maximum face-slab dynamic stresses, the results of the dynamic analysis for the Malutang II CFRD conformed to the general rules, which were shown in the earthquake response and the dynamic FEM analysis response of the same type of CFRD [17, 20, 21, 22, 29].

Fig. 10Distribution of maximum face-slab dynamic stresses for the design earthquake

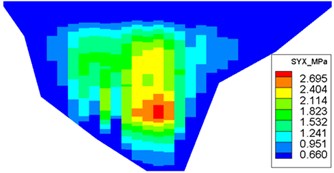
a) Maximum compression stress along the dam slope

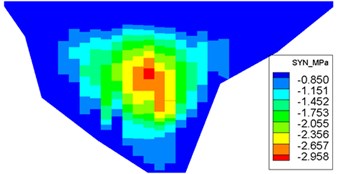
b) Maximum tensile stress along the dam slope

c) Maximum compression stress along the dam axis

d) Maximum tensile stress along the dam axis

Fig. 11Distribution of maximum face-slab dynamic stresses for the check earthquake

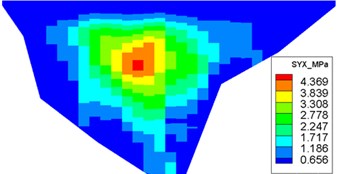
a) Maximum compression stress along the dam slope

b) Maximum tensile stress along the dam slope

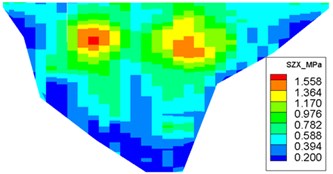
c) Maximum compression stress along the dam axis

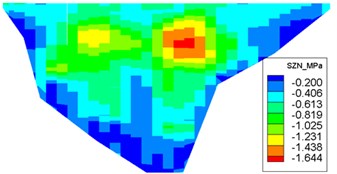
d) Maximum tensile stress along the dam axis

5. Conclusions

According to prototype monitoring of the earth-rockfill dam, $E_0$ of the rockfill were determined by back analysis, which reflected the influences of construction and particle size effect. The $G_{max}$ of rockfill can be analogized according to the statistical relationship and $E_0$. According to $G/G_{max}~\gamma$ and $\xi ~\gamma$ statistic curves, $E_0$, and the analogized $G_{max}$, the $G/G_{max}~\gamma$ and $\xi ~\gamma$ curves of the rockfill were analogized.

The dynamic characteristics of the soil in the Malutang II CFRD were determined by the analogy method. Dynamic analyses by the FEM were performed for a design earthquake and check earthquake. The two earthquake waves exhibited different response spectrums and maximum accelerations. The dynamic responses of the dam conformed to general rules, which were shown in the earthquake response and the dynamic FEM analysis response of the same type of CFRD. It indicates that the analogy method for dynamic characteristics is effective for rockfill and can be employed in a seismic safety check or reinforcement design of a small- to middle-scale earth-rockfill dam that cannot be analyzed by dynamic tests. The best-fit curves of the statistic relationships are the primary orientations for analogy. Furthermore, a sensitivity analysis of the dynamic parameters of rockfill can be determined according to the best-fit curve ± one and two SD of the statistic relationships. The rockfill dynamic characteristics analogy method should be based on an analysis of the predominant influencing factors, such as dam prototype monitoring, construction records, and operation scenarios.