Seismic dynamic responses of earth-rock dam considering wave and seepage

1. Introduction

In the construction of high dams, earth-rock fill dams have become an important choice of dam type. At present, earth-rock fill dams are the majority of the high dams that have been built. Especially in relatively complex conditions, earth-rock dams are often the only choice. In view of the extremely important position of earth-rock dams in the current hydropower development and the complexity of the seismic problems faced by many high earth-rock dams, seismic research of earth-rock dams has become one of the hotspots in the field of dam engineering.

Yang et al. [1] studied dynamic response of different types of high earth-rock dams under ground motion by shaking table test. Wu et al. [2] studied dynamic responses of dam by fully coupled non-linear method, and found that the maximum acceleration amplification factor was located at the top of the dam, and the maximum permanent deformation in both horizontal and vertical directions was located at the top of the dam. Zou et al. [3] found that the impulsive ground motion had great influence on the horizontal displacement and stress of the earth-rock dam by finite element analysis. Cen et al. [4] carried out seismic analysis of earth-rock dams on loess foundation and concluded that liquefaction of dam foundation would be caused under strong earthquake, which would endanger dam safety. Yang and Liu [5] proposed an improved quadratic acceleration integral method for dynamic analysis of earth-rock dam and verified the method accuracy. Shao et al. [6] comprehensively studied the failure process of earth-rock dam through dynamic response analysis. Zhang [7] studied acceleration distribution of earth-rock dam by finite element method and found that the distribution of seismic acceleration along dam height was different from that of low dam. Abdollahi and Attarnejad [8] conducted time domain dynamic analysis of inclined dam-reservoir-foundation interaction using finite difference method. Huang and Xiong [9] presented a new methodology for evaluating the seismic response of earth dams based on a performance-based approach and a stochastic vibration method. Pelecanos [10] investigated effects of dam-reservoir interaction on the nonlinear seismic response of earth dams, obtained that stress and strain development within the dam body were significantly underestimated if dam-reservoir interaction was ignored. Wei et al. [11] proposed a generalized plasticity model used for analysis of the static and dynamic performances of Rumei dam, advantage of the model was that the residual deformation of the dam during the earthquake could be directly obtained, and no additional semi-empirical procedures were needed. Li et al. [12] studied the dynamic responses of earth dam related to new type of polymer antiseepage wall, results shown that the earth dam with a polymer anti-seepage wall had a good capacity for seismic damage resistance. Zhang et al. [13] investigated site amplification effects on seismic response of an earth and rockfill dam and found that wave concentration is the main reason for the high amplifications of the displacement within the dam.

For the combination of wave and earthquake, Li and Huang [14] found that effect of wave was less than that of earthquake, and dynamic response under combined action of wave and earthquake was not a simple accumulation through study of deep-water bridge. Liu et al. [15] analyzed dynamic responses of wind power structure under combined action of large earthquake and wave and obtained that wave force could significantly change the energy distribution of power spectrum of dynamic response compared with the seismic wave alone. Xian et al. [16] found that influence of wave effect on seismic response of isolated bridges was small. He and Li [17] obtained that combined effect of earthquake and wave on different platforms was different, in some cases, it was necessary to consider the combined effects of earthquake and wave. Zheng et al. [18] carried out shaking table test of offshore wind turbines, experimental results revealed that the joint action is important for the proper evaluation of structure response, ignoring wave action would lead to underestimation of response. Cheng et al. [19] discussed dynamic responses of subsea tunnels under the action of ocean waves and earthquakes considering coupling effect of stress and seepage fields. Song [20] pointed out that water infiltration through the cracks softened the material of the surface slope, and the rapid drawdown also enhanced the slope deformation. Ding et al. [21] investigated dynamic response of the pier under combined earthquake and wave-current action and obtained that effect of wave-current action on seismic responses of the pier under combined earthquake and wave-current action was great and could not be ignored.

Although earth-rock dams are widely used in engineering applications, most of the current researches only consider the seismic effect, but effects of waves on dynamic responses are different and cannot be ignored. Some research has shown that dynamic responses of the other structures under the combined action of wave and earthquake are complex, in most cases, it is necessary to consider the combined effects of earthquake and wave. Research on earth-rock dam considering combined effects of seepage, earthquake and wave simultaneously is very limited. In this paper, porous media material is used to simulate seepage flow, considering wave and fluid-solid interaction, a dynamic calculation model of earth-rock dam is established, and Arbitrary Lagrange Eulerian method is used to solve the dynamic problem. Dynamic responses of dam under wave, earthquake and wave+earthquake are comparatively investigated; influences of seismic wave type and PGA on dynamic responses of earth-rock dam are discussed, which can provide references for improving the seismic safety of the earth-rock dam.

2. Fluid-solid interaction dynamic equation

When the earth-rock dam is subjected to wave and earthquake, coupling dynamic equation is as follows:

where $\mathbf{F}$ is hydrodynamic forces caused by wave and earthquake; $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are mass matrix, damping matrix and stiffness matrix; $\ddot{\mathbf{x}}\left(t\right)$, $\dot{\mathbf{x}}\left(t\right)$ and $\mathbf{x}\left(t\right)$ are relative displacement, velocity and acceleration arrays of dam body; $I$ is influence coefficient array of ground motion; ${\dot{\mathbf{x}}}_g$ and ${\ddot{\mathbf{x}}}_g$ are velocity and acceleration of ground motion; $\dot{\mathbf{u}}$ and $\ddot{\mathbf{u}}$ are absolute velocity and acceleration of wave water points, respectively; $v$ is velocity of water flow; $A$ and $V$ are the area of upstream water and the volume of drainage; ${\rho }_w$ is water density; $C_D$ is damping coefficient; $C_M$ is inertia coefficient (mass coefficient); $C_m$ is additional mass coefficient [22].

3. Wave simulation

Wave can be simulated by second-order Stokes equation, and the equation assumes that the fluid is incompressible. The wave motion is defined as potential motion, which can be divided into velocity potential and flow function with orthogonality. By introducing the above assumptions and boundary conditions, the wave surface equation of the second-order finite-amplitude wave at the entrance can be obtained as follows:

where $\eta$ is wave surface; $D$ is water depth; $H$ is wave height; $\omega$ is circular frequency; $L$ is wave length; $m$ is wave number.

Principle of numerical wave-making is to give the initial velocity of the water point at the boundary entrance, and then propagate to the exit. Therefore, there are two kinds of particles at the entrance, one is above the wave surface, that is, the air particle, assuming that the air particle does not move, namely, the initial velocity is 0; the other is below the wave surface, that is, the water quality point. Referring to the wave theory, the horizontal velocity v is given as follows:

4. Stress-seepage coupling equation

Equation can be discreted by Galerkin Weighted Residual method, considering nonlinear characteristics of soil, the displacement increment at time $\mathrm{\Delta }t$ is taken to replace the whole displacement, then the Biot consolidation equation of saturated soil can be discretized into incremental equation, as shown in Eq. (5) [23]:

where $\stackrel{-}{\mathbf{k}}$ is solid stiffness matrix; $\mathbf{k}\mathrm{\text{'}}$ is stress-seepage coupling matrix; ${\mathbf{k}}^T$ is seepage matrix; $\mathbf{B}$ is integral matrix of free surface; $\mathrm{\Delta }\delta$ is node displacement increment; $\mathrm{\Delta }\mathbf{u}$ is node void pressure increment; $\mathrm{\Delta }\mathbf{Q}$ is flow increment matrix; $\mathbf{R}$ is equivalent nodal load; ${\mathbf{R}}_t$ is the part of the load balanced by the displacement that has occurred at time $t$.

Because seepage depends on the full distribution of pore water pressure, which is not dependent on the increment of void pressure, therefore, the void water pressure should be expressed in full form. The total air pressure of element node $i$ at time $t_n$ and $t_{n+1}$ are ${\mathbf{u}}_{i\left(n\right)}$ and ${\mathbf{u}}_{i\left(n+i\right)}$, respectively, and $\mathrm{\Delta }{\mathbf{u}}_i={\mathbf{u}}_{i\left(n\right)}-{\mathbf{u}}_{i\left(n+1\right)}$, Eq. (5) can be changed to:

Under the Biot consolidation assumption, the dynamic equations of porosity $N$ and permeability coefficient $K$ are deduced according to the relevant definition of porosity and Kozeny-Carman equation of seepage mechanics:

where $n_0$ is initial porosity, which is dimensionless; $k_0$ is initial permeability coefficient; ${\epsilon }_v$ is volume strain.

Taking the initial soil porosity $n_0$ as the connection part, the relationship between the overall permeability coefficient $\mathbf{k}$ and the overall permeability coefficient $\mathbf{k}\mathrm{\text{'}}$ affected by the stress field is established:

Combing Eq. (9) and Eq. (5), consider aggravating residuals, and the numerical equation of stress-seepage coupling is obtained after simplifying the deformation:

where $\mathbf{B}$ is slope matrix of dynamic water; $\mathbf{K}$ is element permeability coefficient matrix; $\mathbf{H}$ is node head vector; $\mathbf{N}$ is form function vector; $q$ is unit weight of element boundary; $m_w$ is choke coefficient; ${\gamma }_w$ is water volume density; $H_t$ is time-varying water head [24].

5. Numerical example

5.1. Calculation model

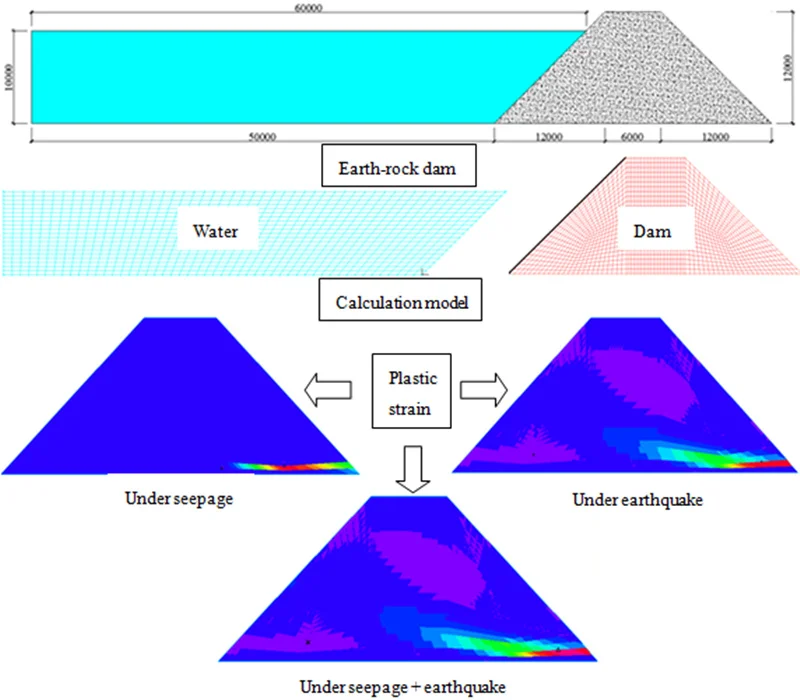
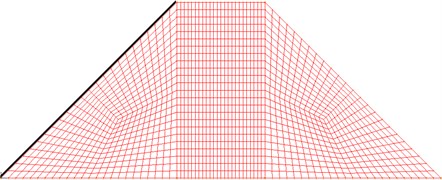
2-D Solid element and Mohr-Coulomb material are used to simulate earth-rock dam, the corresponding material parameters are shown in Table 1 [25]. Besides, porous medium is defined to consider the seepage effect, and permeability coefficient is 3.5×10^-6 m/s. 2-D Fluid element and Constant material are used for simulating water; it is assumed that the liquid is incompressible, the viscous coefficient is 2×10^-5, the density is 1000 kg/m³, and the bulk modulus is 2.3×10⁹. FSI Boundary is set at the position where earth-rock dam and water interact; non-slip boundary (Wall boundary) condition is set at the bottom of the water; free surface is set to simulate the sloshing behavior of water. Wave is simulated by applying velocity load, and the peak value of wave velocity is 2 m/s. Geometric model and numerical calculation model are shown in Figs. 1 and 2 [26].

Table 1Material parameters of earth-rock dam

Items	Density $\rho$ / (kg·m-3)	Elastic modulus $E$ / MPa	Cohesion $c$ / kPa	Friction angle $\phi$ / (°)	Poisson’s ratio $\nu$
Value	2200	80	60	20	0.3

Fig. 1Geometric model (unit: mm)

Fig. 2Numerical calculation model

a) Earth-rock dam

b) Water

5.2. Comparisons of dynamic responses of dam body under different actions

Earth-rock dams are likely to be subjected to earthquake or wave during their life cycle, and the more serious situation maybe the simultaneous action of earthquake and wave. In order to further improve the safety of earth-rock dam, it is necessary to compare dynamic responses of earth-rock dams under wave, earthquake and combined action of earthquake and wave. El-Centro wave is selected for time history analysis and its PGA is adjusted to 0.40 g. Comparisons of the specific results are shown in the Figs. 3-6.

Fig. 3Horizontal displacements of dam body under different loads

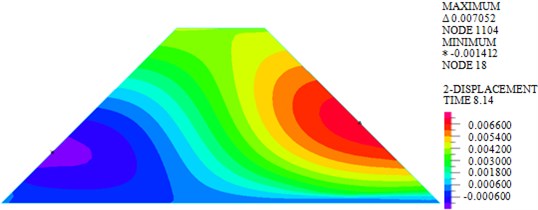
a) Wave

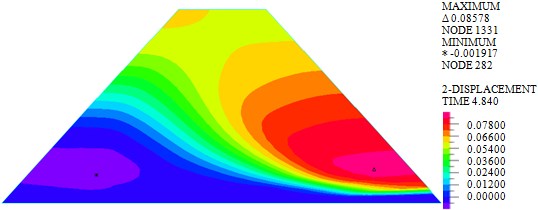
b) Earthquake

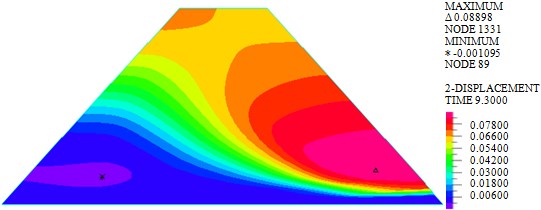
c) Wave + earthquake

As shown in Fig. 3, the maximum horizontal displacements of earth-rock dam under wave, earthquake and wave + earthquake are 7.052 mm, 85.780 mm and 88.980 mm, respectively. It can be seen that horizontal displacement under earthquake action is significantly larger than that under wave action, the combined action of earthquake and wave will further increase horizontal displacement. The maximum horizontal displacement is located in the middle of the back of earth-rock dam under wave action, but the maximum horizontal displacement will move down under earthquake action.

Fig. 4Vertical displacements of dam body under different loads

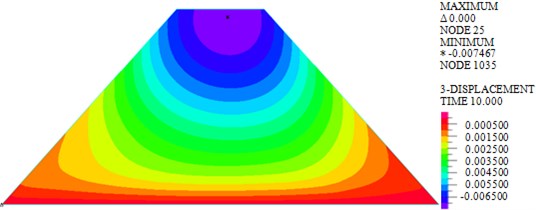
a) Wave

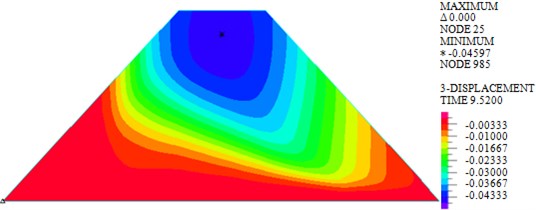
b) Earthquake

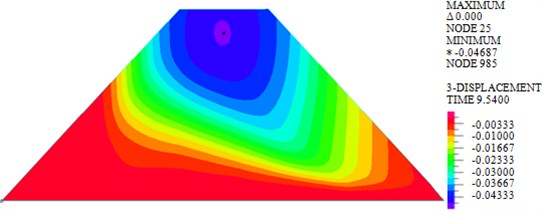
c) Wave + earthquake

As shown in Fig. 4, the maximum vertical displacements of earth-rock dam under wave, earthquake and wave + earthquake are 7.467 mm, 45.970 mm and 46.870 mm, respectively. It can be seen that effect of earthquake on vertical displacement of earth-rock dam is obviously greater than that of wave action, and wave will increase the vertical displacement of earth-rock dam under earthquake action to a certain extent. Under wave action, the distribution of vertical displacement of earth-rock dam is basically symmetrical, but the seismic action will make the vertical displacement field distribution of earth-rock dam change significantly.

Fig. 5Maximum shear stresses of dam body under different loads

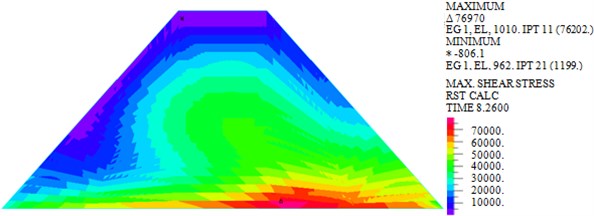
a) Wave

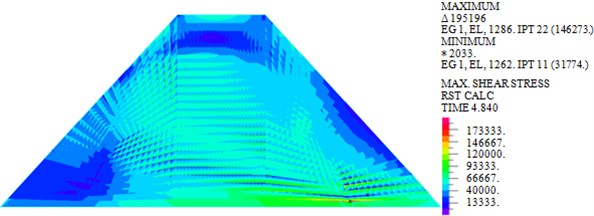
b) Earthquake

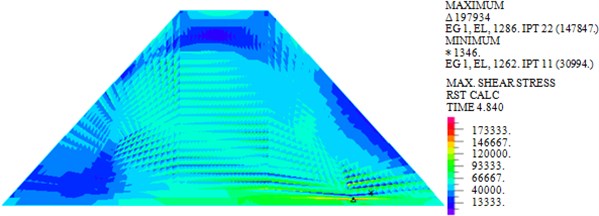
c) Wave + earthquake

As shown in Fig. 5, the maximum shear stresses of earth-rock dam under wave, earthquake and wave + earthquake are 76.202 kPa, 146.273 kPa and 147.847 kPa, respectively. It can be seen that the maximum shear stress under earthquake action is obviously larger than that under wave action, comparing the two cases of earthquake and earthquake + wave actions, it can be seen that combined action has little influence on the maximum shear stress of earth-rock dam, which can be neglected.

As shown in Fig. 6, the maximum plastic strains in $YZ$ plane of earth-rock dam under wave, earthquake and wave + earthquake are 0.0048, 0.1389 and 0.1438 kPa, respectively. It can be seen that the plastic strain under earthquake action is significantly larger than that under wave action, and the plastic strain increases significantly under the combined action of wave and earthquake. The plastic strain distribution under wave action is small, but the plastic strain distributions under earthquake and wave + earthquake actions are wide.

5.3. Comparison of dynamic responses under earthquakes with different characteristics

The propagation mechanisms of near-field and far-field earthquakes are very different, which makes their effects on the dynamic response of the system different.

Fig. 6Plastic strains in YZ plane of dam body under different loads

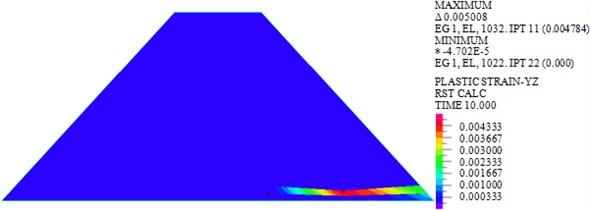
a) Wave

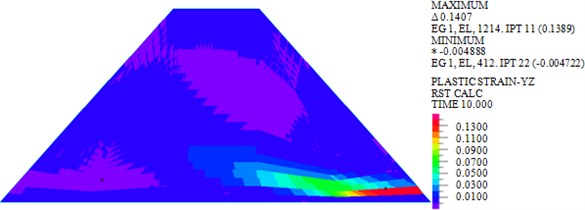
b) Earthquake

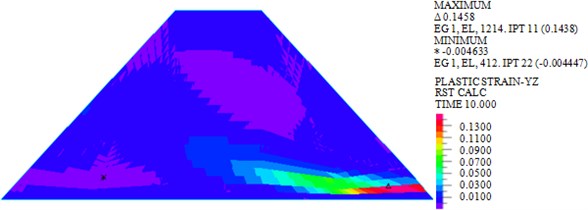
c) Wave + earthquake

Near-field El-Centro wave and far-field long-period Tianjin wave are selected to conduct time history analysis, and their PGAs are adjusted to 0.2 g. The comparisons of horizontal displacement, vertical displacement, maximum shear stress and plastic strain of dam under two kinds of earthquakes are shown in Figs. 7-10.

As shown in Figs. 7-10, under actions of near-field El-Centro wave and far-field long-period Tianjin wave, the maximum horizontal displacements are 18.30 mm and 33.97 mm, the maximum vertical displacements are 12.04 mm and 20.25 mm, the maximum shear stresses are 82.693 kPa and 103.339 kPa, and the maximum plastic strains in $YZ$ plane are 0.0244 and 0.05276. It can be seen that larger horizontal displacement of dam body will be caused by long-period long-field earthquake, vertical displacement, and shear stress and plastic strain of dam under long-period long-field earthquake are obviously larger than that under near-field earthquake.

Generally speaking, the influence of far-field long-period earthquake on earth-rock dam is obviously greater than that of near-field earthquake, and the influence of long-period earthquakes on deformation response of earth-rock dams is greater than that on shear stress. Therefore, in order to ensure the seismic safety of earth-rock dam, the influence of different characteristic earthquakes should be reasonably considered in the engineering application of earth-rock dams.

Fig. 7Horizontal displacements under earthquakes with different characteristics

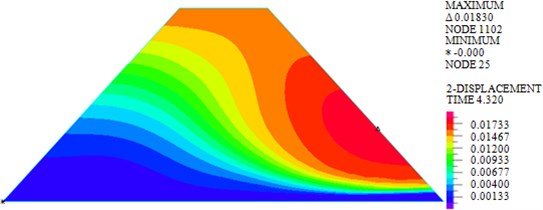
a) El-Centro

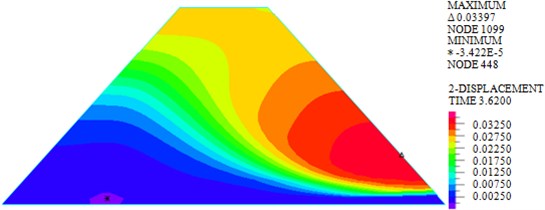
b) Tianjin

Fig. 8Vertical displacements under earthquakes with different characteristics

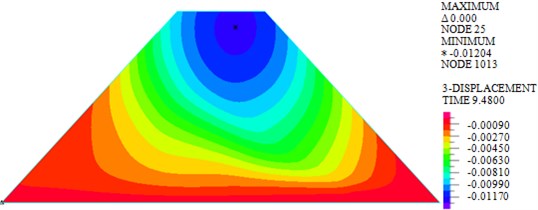
a) El-Centro

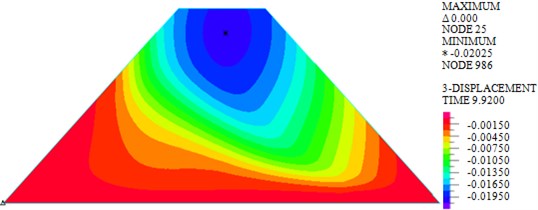
b) Tianjin

Fig. 9Maximum shear stresses under earthquakes with different characteristics

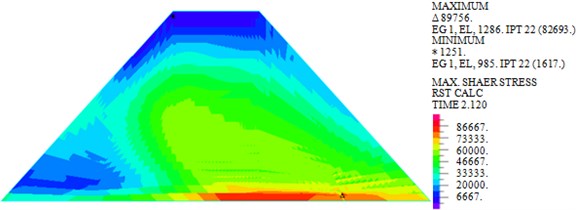
a) El-Centro

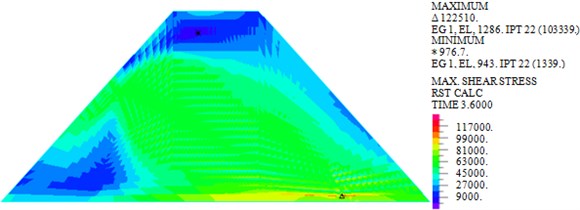
b) Tianjin

Fig. 10Plastic strains in YZ plane under earthquakes with different characteristics

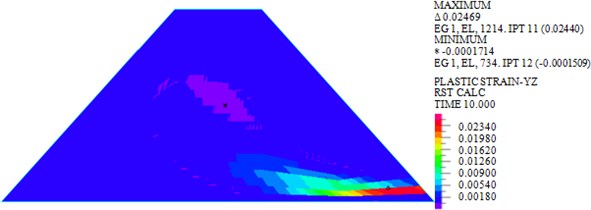
a) El-Centro

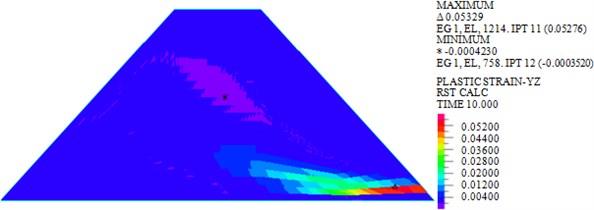
b) Tianjin

5.4. Influence of PGA on dynamic responses

PGA is one of the three essential factors of seismic wave, and it is also one of the important parameters to be considered in design. In order to study the influence of PGA on dynamic responses of earth-rock dam, ChiChi wave, El-Centro wave, Kobe wave and Northridge wave are chosen as seismic input, their PGAs are adjusted to 0.1 g, 0.2 g, 0.3 g, 0.4 g and 0.5 g based on incremental dynamic analysis principle. The dynamic responses of earth-rock dam are studied with the change of PGA, and the detailed calculation results are shown in Fig. 11.

As shown in Fig. 11, although horizontal displacement, vertical displacement, maximum shear stress and plastic strain of earth-rock dam increase with the increase of PGA, the increase magnitude is different. El-Centro wave has a relatively small effect on earth-rock dam, and Kobe wave has the most disadvantageous effect on earth-rock dam, which shows that the characteristics of seismic wave is an important factor affecting the dynamic response of earth-rock dam. With the increase of PGA, the increasing trends of horizontal displacement, vertical displacement and plastic strain increase greatly, but the increasing trend of maximum shear stress slows down. Results show that deformation of earth-rock dam is large under strong earthquake, which makes the bearing capacity of dam body be decreased, and then easily leads to dam break.

Fig. 11Influence of PGA on dynamic responses

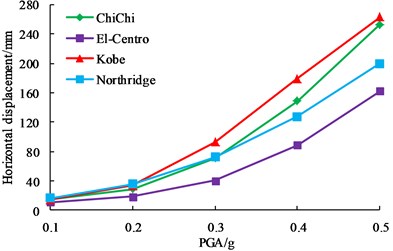
a) Horizontal displacements

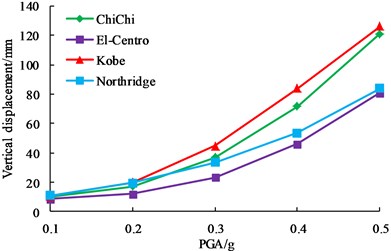
b) Vertical displacements

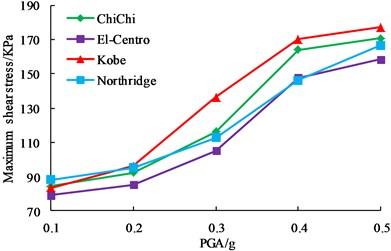
c) Maximum shear stress

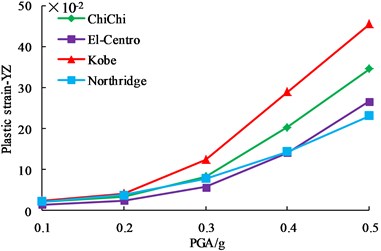
d) Plastic strains in $YZ$ plane

6. Conclusions

Considering dam seepage, wave action and fluid-solid interaction, a numerical calculation model is established, and ALE method is used to solve the nonlinear dynamic coupling problem. Dynamic responses under wave, earthquake, and combined of wave and earthquake are investigated comparatively. The main conclusions are as followings:

1) Effect of earthquake on dynamic responses is obviously greater than that of wave action, and combined action of wave and earthquake has influence on dynamic response. Nephograms of dynamic responses under wave and earthquake actions are very different.

2) Dynamic responses under far field long period earthquake is obviously greater than that under near field earthquake, influence of long period earthquake on deformation of earth-rock dam is obviously greater than that on shear stress, for example, distribution of plastic strain is wider. Therefore, influence of different characteristic earthquakes should be reasonably considered in the design of earth-rock dam.

3) With the increase of PGA, dynamic responses of earth-rock dam are increased, the increasing trends of horizontal displacement, vertical displacement and plastic strain become drastically, while the increasing trend of maximum shear stress slows down.

4) When earthquake intensity is large, earth-rock dam is easy to be damaged due to excessive deformation.