Abstract
The hydrocyclone of main diameter 28mm with a typical variable diameter pipe structure was selected as the research object, and the interaction of the fluid and the structure was considered on the basis of the hypothesis of small deformation. The two-way fluid structure interaction (FSI) model of the hydrocyclone with variable diameter pipes was presented in this paper, and the related numerical simulation and experimental research was also carried out. The structure vibration characteristics of the structure were analyzed base on the fluid structure interaction, and the vibration characteristics of the structure were obtained. The vibration characteristics of the between the results of numerical simulation and experimental were consistent. Through above analysis showed that the two-way FSI calculation model of hydrocyclone with variable diameter pipe was reasonable. The influence of coupling effect on flow field couldn’t be ignored. The interaction between fluid and structure changed the movement characteristics of the structure, which should be considered in the design and application of hydrocyclone.
1. Introduction
The influence of high water cut on oil and gas production and recovery has attracted much attention. The water content of crude oil is increased, which not only increases the process flow of ground gathering and transportation and water treatment, but also increases the risk of investment and environmental pollution. Therefore, it is urgent to need new oil production technology and equipment to meet the needs of oil recovery.
Downhole oil-water separation technology, it is in the high water cut wells, the separation equipment combined with improved power pump, realization of down-hole oil-water separation and separation of water reinjection, with simplified process, energy saving, environmental protection and many other advantages. The down-hole oil-water separation process can be effectively implemented, which depends on the separation performance of the down-hole separation equipment, high separation performance needs to be separated from the device with a relatively stable flow field. However, during the operation of the process tubing string, the periodic motion of the power pump will bring the vibration of the hydrocyclone, interaction between structural vibration and internal two phase fluid, which makes the oil-water two-phase flow become more complex, and the influence on the fatigue life of the process tubing string. Therefore, the understanding of the natural frequency and vibration mode of the structure of the down-hole separation equipment can prevent the resonance damage, vibration fatigue, and provide the basis for improving the performance and reliability of the separation equipment.
Existing on the study of the vibration characteristics of the structure, it is found that the effect of the fluid on the structure is neglected and the results are not consistent with the actual situation. Jin Changming [1] using the modal analysis method, the fluid structure interaction analysis is carried out for the liquid filled elbow pipe. The natural frequency of the pipe is reduced, but the effect on the mode shape is small. Pellicano [2] studies the finite long axis symmetric cylindrical thin shell structure and liquid coupling system, discusses the influence of structural size of nonlinear behavior. Chang Y. S. [3] using FSI method to analyze the carrying capacity of the thin wall pipe, it is suggested that the effect of the fluid should be considered in the safety evaluation of the thin wall pipe. Yu Meng [4] studies vibration characteristics of pipes conveying under different constraint conditions, and the radial displacement, stress, natural frequency and mode shape of the pipe wall are obtained. The author considered the influence of fluid-structure interaction, combining with numerical simulation and experimental test method, analyzed the coupling effect of the hydrocyclone with variable diameter pipe structure, and obtained the vibration characteristics of the structure of the hydrocyclon. In order to evaluate the reliability of down-hole oil-water separation technology, it has important values for the optimization design of the structure.
2. The FSI model and method
2.1. The geometric model
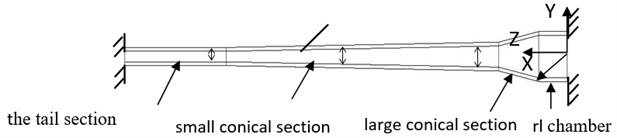
The hydrocyclone of main diameter 28 mm with a typical variable diameter pipe structure was selected as the research object, and materials for organic glass, structure of operation, both ends of the pipes are fixed, Considering the vibration of the structure of the hydrocyclone in the internal fluid pulsation, and the structure and the turbulent flow in the pipe form a fluid structure coupling system. Its mechanical model is shown in Fig. 1.
Fig. 1The fluid structure interaction mechanics model of variable diameter pipe
2.2. FSI calculation model and method
Fluid elements of the hydrocyclone with variable diameter pipes satisfy the conservation of mass and momentum equations.
Continuous equation is:
The momentum conservation equation is:
The balance equation of solid part is:
Fluid-structure interaction interface equation is:
here, the temperature change of the fluid in the hydrocyclone was not considered, and the force and displacement are equal in the fluid and the solid interface needs to be satisfied, respectively.
Where, is local acceleration vector of solid (m/s2), and are volume force vector of fluid and solid (N), respectively. and are density of fluid and solid (Kg/m3), respectively. is velocity vector of fluid, is Cauchy stress tensor (N), is interface stress of fluid (N), and are interface displacement of fluid and solid (m).
The inherent characteristics of the structure under the coupling action are studied, and the effect of the fluid pressure on the structure is considered. Without considering the influence of the external force and the damping on the system, the dynamic equation of the hydrocyclone can be changed into:
Here, let us suppose that is:
Then the Eq. (6) is changed to:
where, is a coupled mass matrix.
Let’s assume that:
where, is the solution of Eq. (8); is the first order modal vibration mode vector; is the order natural frequency of the modal (rad/s).
The Eq. (9) into Eq. (8) to:
The necessary and sufficient conditions for the existence of nonzero solutions of the Eq. (10) are:
The order natural frequency of the output:
In this way, we can get the modal parameters of hydrocyclone under FSI.
In the numerical calculation method, the fluid field using the finite volume method, the Reynolds stress turbulence model of turbulence is chosen for the calculation of fluid model, and the method of ALE is adapted to for fluid dynamic mesh. Based on the finite element theory with hypothesis of small deformation, the Newmark time integration method is used to solve the dynamic equation of variable diameter pipe structure in solid domain. Using alternating iterative coupling solving method, the two-way FSI calculation model of hydrocyclone with variable diameter pipe is established. Inlet boundary conditions are chosen by the entrances of hydrocyclone, and outlet boundary conditions are adopted by underflow and overflow of hydrocyclone.
3. Structural modal analysis under FSI
3.1. The instruments and equipment of test
Fig. 2 shows hydrocyclone entity of experimental test, the pressure electric sensor was installed directly in the hydrocyclone with variable diameter pipe, the acceleration sensors of PCB ICP were adopted. Vibration signal was obtained using LMS channel 24 SCADAS mobile data acquisition system and signal analysis using analysis software of LMS. Test Lab. The vibration waveform is shown in Fig. 3.
Fig. 2Entity structure of hydrocyclone

Fig. 3Signal gathering analytical instruments

3.2. Experimental parameters
The experiment was carried out with hydrocyclone of organic glass materials under three kinds of conditions, namely: without medium, full of medium and operating condition with three kinds of flow velocity. The test schemes were shown in Table 1.
Table 1The test scheme
Test sequence | 1 | 2 | 3 | ||
Test condition | Without medium | Full of medium | Operating condition m/s | ||
6.82 | 8.17 | 10.2 | |||
3.3. Arrangement of measuring points
Ten measuring points were arranged on the hydrocyclone, the position of measuring points as shown in Fig. 4. Considering the geometric model in circular symmetry, the structure is simplified into a bar, and measuring points were measured in the same section position of the and axes direction.
Fig. 4Measuring point distribution on variable diameter pipe

3.4. Test method
According to modal theory to determine the vibration characteristics of the hydrocyclone with variable diameter pipe structure, need to measure the transfer function. The way of single input single output was adopted in this test. The forces acting on the structure depended on the action of pulse hammer or flow medium, and the response of each point was measured, namely, the structure of hydrocyclon with conditions of without medium and full of medium but not flow was applied exciting force by hammer, and the structure with operating condition was applied impact force by fluid. Then the measured signal was processed and analyzed, and the transfer function between the excitation point and the response point was calculated.
In the test device shown in Fig. 2, the foundation of the structure is fixed on the ground, and the admittance of the connection point is zero. According to the vibration theory, influence of low order modal of vibration of the structure, is bigger than higher order modal can be ignored, and the influence of higher order modal can be neglected. So the frequency ranges of 0-500 Hz, and frequency resolution precision is 0.5 Hz.
4. Analysis of vibration characteristics of hydrocyclone
4.1. Experimental modal analysis under the condition of no medium
The output signal of ten measuring points of hydrocyclone without medium were measured. Modal identification state diagram as shown in Fig. 5, peaks and troughs of wave of two curves overlap together and at the intersections have a list of S and V letters, S denote that frequency, damping and vector of the pole are stable, V denote that vector is stable, O denote that the noise is presence in this location, the curve of troughs of wave denote imaginary frequency curve, and the curve of peaks of wave denote real frequency curve. The frequency range of 0-500 Hz are shown in in Fig. 5, and we can see the first three order modal identification are clear, the position of peaks and troughs of wave of two curves overlap together are natural frequency of the hydrocyclone structure.
Fig. 5The modal identification state diagram of hydrocyclon
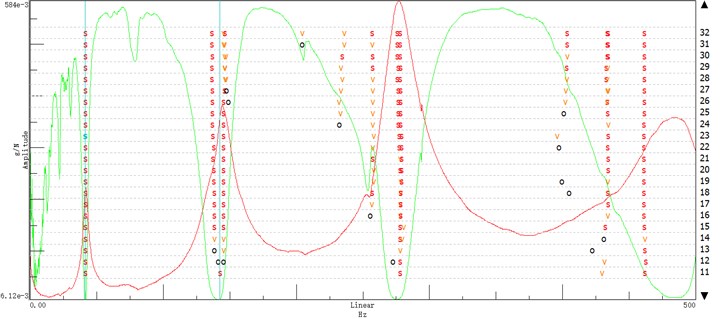
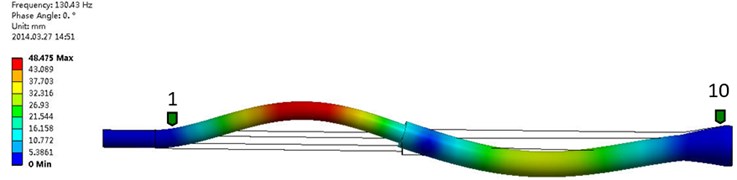
The experimental test and numerical simulation were carried out under the same conditions of no medium, and results of experimental test and numerical simulation were compared and analyzed. The first two natural frequencies and model shape of the hydrocyclone structure were given from Fig. 6 to Fig. 9. The first three natural frequencies and model shape of the hydrocyclone structure were given in table 2. As can be seen from the chart, the natural frequency and model shape of the hydrocyclone structure between numerical simulation and experimental test were similar, the relative error increased with the increase of the order, the error of the three order was the maximum, and the relative error was 8.8 %.
Based on the measured and simulated results, we could have got that measure point 4 and measure point 5 were greatly deformation in the first-order model shape, where is the small conical section of hydrocyclone structure near the junction with the tail section. The deformation of measure point 3 was larger in second-order model shape; this location is near the middle of the tail pipe section.
Table 2The condition of experimental test
Order | Natural frequency of experimental test / Hz | Natural frequency of numerical simulation / Hz | Relative error |
1 | 41.65 | 43.58 | 4.63 % |
2 | 142.74 | 130.43 | 8.62 % |
3 | 261.23 | 238.25 | 8.80 % |
Note: The expression of relative error is , where is relative error, and are natural frequency of experimental test and natural frequency of numerical simulation, respectively | |||
Fig. 6The first order frequency and modal shape of experimental test (Mode 1: 41.6534 Hz, 4.31 % AMPS)

Fig. 7The first order frequency and modal shape of numerical simulation
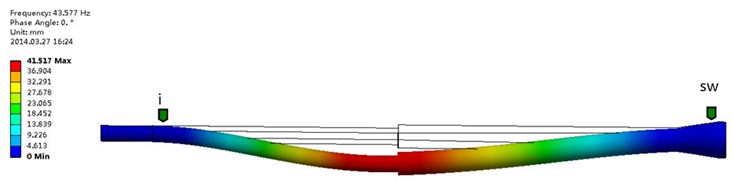
Fig. 8The second order frequency and modal shape of experimental test (Mode 2: 142.7441 Hz, 5.17 % AMPS)

Fig. 9The second order frequency and modal shape of numerical simulation
4.2. Experimental modal analysis under full of medium
In the hydrocyclone, the water was filled and carried on the modal test analysis, and the natural frequency and the model shape of experimental test and numerical simulation were shown in Figs. 10-13 and Table 3. As can be seen from the figure and table, the forms of movement between experimental test and numerical simulation were similar, but the value of the structure with full of medium was lower than natural frequency of without medium, the frequency of experimental test from first order to three order were reduced 2.76 Hz, 12.2 Hz and 6.54 Hz, respectively. And the frequency of numerical simulation from first order to three order were reduced 3.24 Hz, 9.28 Hz and 17.67 Hz, respectively. graphs and tables. This is mainly due to the result in the presence of the internal fluid added mass of the structure.
According to program of Table 1, the modal test analysis of the structure of the hydrocyclone was carried out with inlet velocity of 6.82 m/s, 8.17 m/s and 10.2 m/s, respectively. At the same time the results of numerical simulation were obtained base on fluid structure interaction, and the results were compared between the experimental test and the numerical simulation. Figs. 14-19 showed the first three order model of the inlet velocity of 6.82 m/s. The results of the first three order natural frequencies and the relative error of the different inlet velocity were given in Table 4.
Table 3The test and simulation result
Order | natural frequency of experimental test / Hz | natural frequency of numerical simulation / Hz | Relative error |
1 | 38.89 | 40.34 | 3.73 % |
2 | 130.54 | 120.75 | 7.50 % |
3 | 255.24 | 220.58 | 13.58 % |
Fig. 10The first order frequency and modal shape of experimental test (Mode 1: 38.8890 Hz, 3.99 % AMPS)

Fig. 11The first order frequency and modal shape of numerical simulation
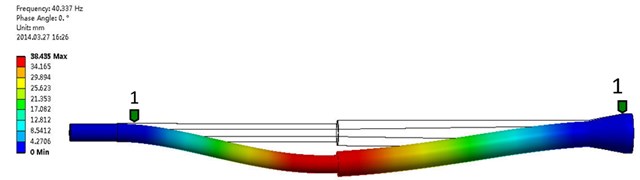
Fig. 12The second order frequency and modal shape of experimental test (Mode 2: 130.5435 Hz, 5.87 % AMPS)
Fig. 13The second order frequency and modal shape of numerical simulation
As can be seen from the chart, the forms of movement between experimental test and numerical simulation were similar. As the inlet velocity increases, the natural frequency is slightly lower, but the range of reduction is smaller. This is mainly in the process medium flows, under the effect of fluid-structure interaction, the force of fluid acted on the structure of hydroclone and embodied by the prestressing form. Under the experimental conditions of range of inlet velocity, the error value of natural frequency of first order between the experimental test and numerical simulation is minimized, while the error value of natural frequency of third order is maximum and maximum is 17.1 %.
Table 4The results of test and simulation under operating condition
Order | Natural frequency of experimental test / Hz | Natural frequency of numerical simulation / Hz | Relative error | |
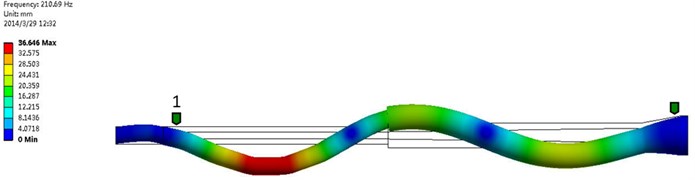
6.82 m/s | 1 | 36.42 | 37.72 | 3.57 % |
2 | 132.49 | 112.53 | 15.07 % | |
3 | 251.10 | 210.69 | 16.09 % | |
8.17 m/s | 1 | 35.92 | 37.07 | 3.20 % |
2 | 129.25 | 110.60 | 14.43 % | |
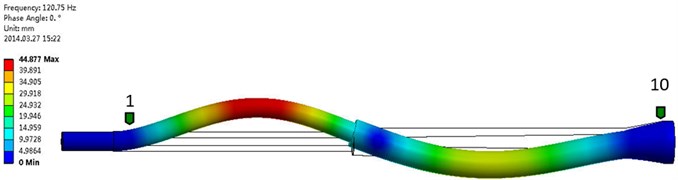
3 | 248.45 | 207.09 | 16.65 % | |
10.20 m/s | 1 | 35.36 | 36.47 | 3.14 % |
2 | 127.88 | 108.81 | 14.91 % | |
3 | 245.78 | 203.74 | 17.10 % | |
Fig. 14The first order frequency and modal shape of experimental test (Mode 1: 36.4213 Hz, 0.11 % AMPS)

Fig. 15The first order frequency and modal shape of numerical simulation
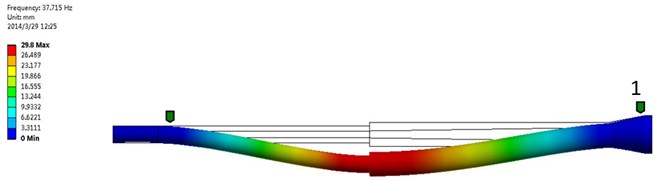
Fig. 16The second order frequency and modal shape of experimental test (Mode 2: 132.4906 Hz, 4.78 % AMPS)

Fig. 17The second order frequency and modal shape of numerical simulation
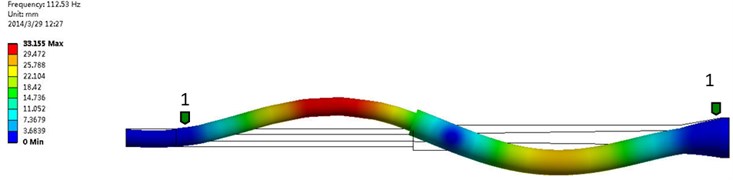
Fig. 18The third order frequency and modal shape of experimental test (Mode 3: 251.1038 Hz, 3.28 % AMPS)
Fig. 19The third order frequency and modal shape of numerical simulation
5. Conclusions
1) Using the modal analysis theory, the vibration test and analysis of the structure of the hydrocyclone of organic glass materials were carried out. The natural frequencies and model shapes of hydroclone were obtained in the absence of the medium, full of medium and working conditions, and value of natural frequency of the same order is gradually low with the status of without medium, full of medium, operating condition and increased inlet velocity in turn. And maximum response position of the hydroclone is located in the small conical section of hydrocyclone near the junction with the tail section.
2) The numerical simulation analysis of fluid structure interaction in the hydrocyclone was carried out, and the results are compared between the numerical simulation and experimental test. The model shapes and the first order natural frequencies between experimental test and numerical simulation were similar, and the maximum error is 4.63 %. While the error of the natural frequencies of second and third order is relatively large, the maximum is 17.10 %.
3) Studies show that the effect of fluid on the vibration characteristics of the structure cannot be ignored, need to be given full consideration in the design and application. In addition, the amplitude of deformation of the small conical section of the hydrocyclone near the junction with the tail section is large, need to consider adding support to increase the stability of the device for practical applications of the hydrocyclone.
References
-
Jin Changming, Wang Gancheng, Gao Kong, et al. Analysis of fluid-conveying pipe with transfer matrix method. Noise and Vibration Control, Vol. 6, 2009, p. 30-33.
-
Pellicano F., Amabili M., Paı̈doussis M. P. Effect of the geometry on the non-linear vibration of circular cylindrical shells. International Journal of Non-Linear Mechanics, Vol. 37, Issue 7, 2002, p. 1181-1198.
-
Chang Y. S., Song K. H., Sang M. L., et al. Fluid structure interaction analysis on wall thinned pipes. Key Engineering Materials, Vols. 321-323, 2006, p. 670-673.
-
Yu Meng Analysis on characteristics of fluid-structure interaction for fluid conveying pipes by ANSYS. Chinese Journal of Ship Research, Vol. 5, 2007, p. 54-57.
About this article
This work was supported by the National Natural Science Foundation of China (Grant Nos. 11402051, 11172061).
