Abstract
In order to study the flow-induced vibration characteristics of the natural gas vent pipeline under the internal flow field, taking the gas transmission station pipeline as an example, the ANSYS Workbench software was used to establish models under two working conditions, uncoupling and fluid-solid coupling, for modal analysis, and analyze and compare the calculation results and propose a structural improvement plan. The results show that the maximum amplitude of the first three modes under the two working conditions is concentrated on the riser mouth, and the amplitude under the fluid-solid coupling condition is slightly larger than that of no coupling; the inner diameter of the pipe elbow is large and the pressure is small, and the outside diameter is small and the pressure is small. Large, this instability will increase the air pulsation of the flow field. In the improved scheme, adding a restriction on the top to increase the rigidity of the pipeline can significantly reduce the maximum amplitude of the gas pipeline; adding an orifice to eliminate air flow pulsation has a certain effect on reducing the maximum amplitude and natural frequency, and the combination of the two can make the pipeline more stable. The research results of this paper can provide improved ideas for vibration reduction at the natural gas venting operation site.
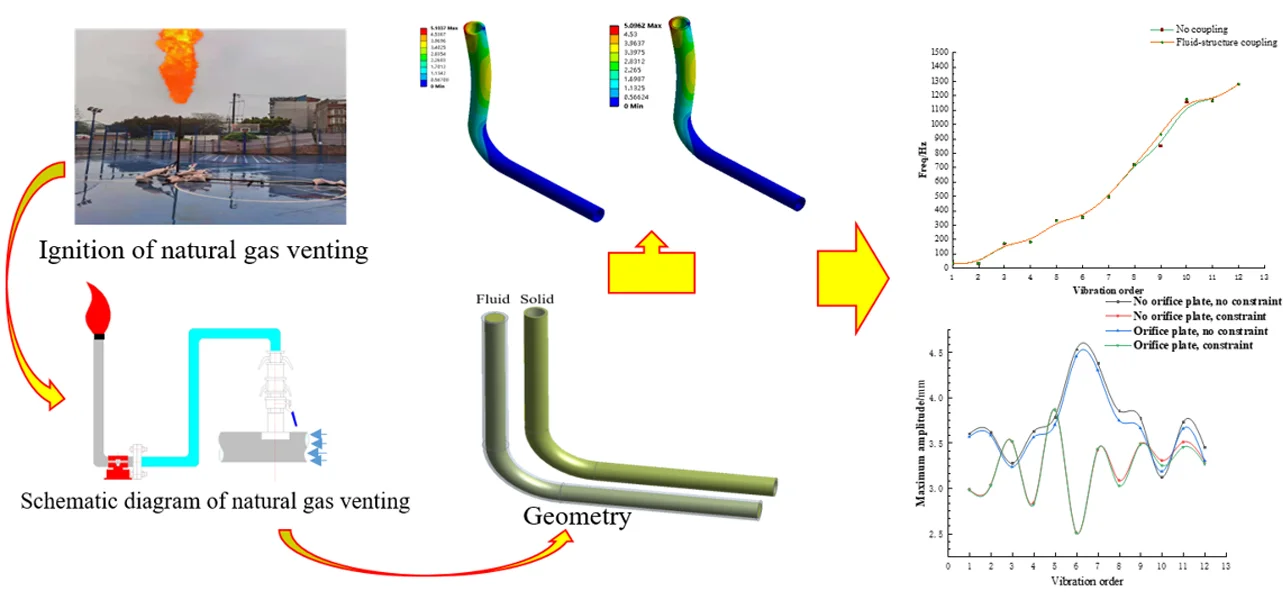
1. Introduction
The venting system is an important facility for long-distance gas pipelines, which plays an important role in ensuring the safety of pipeline maintenance and emergency repairs and reducing the hazards of pipeline accidents [1]. During gas pipeline expansion, renovation, overhaul and emergency repair [2], in order to ensure operational safety, the natural gas in the pipe section needs to be completely evacuated through the venting system, and inert gas such as nitrogen is injected into the pipe section to replace the remaining natural gas [3]. When venting, it is usually necessary to use a riser and a torch to ignite natural gas. However, due to the large height of the riser, the stability is poor, and the natural gas in the unsteady flow state at the bend connecting the horizontal pipe and the riser is prone to vibration, which will affect the surrounding environment and construction. There is a greater threat to personnel. Therefore, it is of great significance to reduce the vibration of the vent pipeline and enhance its structural stability.
Zhang Ke [4] used critical flow numerical calculation and transient simulation calculation of TGNET Pipeline Studio software to study the venting operation process control and venting time measurement method, and compared with the actual venting operation process, it was concluded that the construction pipeline venting operation It is related to the inherent physical parameters such as pipe length, diameter and pressure. Li Yutian and others used FLARE-NET and PHAST software to determine the Mach number, noise intensity and natural gas diffusion radius corresponding to the maximum discharge flow of different venting methods. Cen Kang [5] used FLACS to analyze the dynamic process of the fire transfer tube of a typical ground deflagration ignition device, and discussed the influence of the volume fraction of combustible gas in the fire transfer tube, the filling rate of combustible gas and the length of the fire transfer tube on its ignition performance. Zhang Yong [6] and others analyzed the China-Myanmar natural gas pipeline to determine the initial pressure of its venting, select a feasible venting method, calculate the venting time, and evaluate its impact on the environment. Li Longdong [7] et al. compared the three methods of venting and pressure reduction of gas pipelines at home and abroad, and verified by the practice of centralized hot process disposal in the second and third lines of the West-East Gas Pipeline, and summarized a use of gas pipeline compressors. Stepped pressure reduction method in which multiple pipe sections are continuously pressure-reduced and then vented. Feng Sheng [8] and others analyzed the change law of air volume, vent temperature, pipeline pressure, pipeline temperature and other parameters during the venting process. The structural behavior of submarine natural gas transmission pipelines is simulated with the aid of a finite difference numerical model [9].
The natural gas venting ignition pipeline has nonlinear vibration. The current researches on nonlinear vibration include the nonlinear vibrations of a contact-mode atomic force microscopy(AFM) model subjected to multi excitations are controlled via a time-delayed positive position feedback (PPF) controller [10], M. Sayed et al. applied active control to the nonlinear dynamic beam system to eliminate its vibration [11], Ali Kandil first derived a nonlinear dynamic equation for controlling the lateral vibration of a controlled system under a constant stiffness coefficient [12], the work of N. A. Saeed et al. aims to study and control the nonlinear dynamic behavior of a nonlinear asymmetric shaft system [13, 14], Y. S. HAMED et al. studied the nonlinear dynamics control of a contact atomic force microscope system using a time-delay proportional-differential controller [15, 16].
However, the above studies have rarely studied the vibration characteristics of vented horizontal pipes and risers. Therefore, this paper uses finite element software to establish a pipe model, analyzes the vibration characteristics of the model under fluid-solid coupling conditions, and conducts the structure Structural improvements.
2. Model building
2.1. Basic mathematical model of fluid-structure interaction
The pipe is connected to the atmosphere at one end, so the natural gas in the pipe can be regarded as uncompressed gas. The fluid continuity equation and momentum equation are.
Continuity equation:
Equation of motion in integral form:
where: is the fluid density, kg/m3; is the time, s; , , and are the velocity components on the , , and coordinates respectively, m/s; is any finite value in the flow field at time the volume of the control body, m3; is the enclosed area, m2; is the fluid combined velocity, m/s.
It is an unsteady flow state in the pipeline, and the streamline bending degree of the fluid at the transition bend of the riser pipe and the horizontal pipe is relatively large. In this paper, the Realizable - model is selected:
where is the turbulent kinetic energy; hourly average speed; turbulent viscosity; is the dissipation rate of turbulent kinetic energy; is time, s; , is the Prandtl number corresponding to turbulent kinetic energy and dissipation rate, = 1.0, = 1.2; is the correction factor; is empirical constant, = 1.9; is the production term of the turbulent kinetic energy caused by the average velocity gradient.
2.2. Finite element model
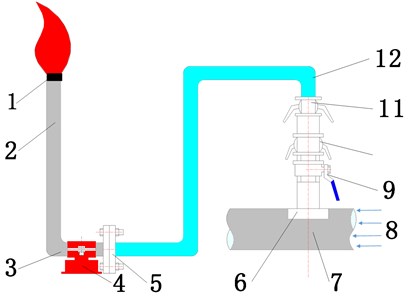
The schematic diagram of natural gas venting is shown in Fig. 1. The gas is ignited through the main pipe, hose, and metal horizontal pipe riser. During the operation, the riser height is large, the structural rigidity is low, and the unstable airflow in the pipe causes the pipeline to vibrate. Phenomenon. Due to the existence of open flames, the continuous vibration of the pipeline will cause danger to the surrounding environment and construction personnel. This article specially analyzes the vibration characteristics of the L-shaped pipe.
Fig. 1Ignition of natural gas venting

Fig. 2Schematic diagram of natural gas venting: 1 – torch; 2 – stand pipe; 3 – horizontal pipe; 4 – horizontal pipe fixed support; 5 –flange; 6 – plate; 7 – main pipe line; 8 – natural gas; 9 –valve; 10 – clamp type quick change joint; 11 – clamp type quick change joint; 12 – flexible tube
The model in this paper uses Solid works 3D modeling software to build the pipeline, and then imports the ANSYS software. The pipeline material is structural steel. Young’s modulus is 206 GPa, Poisson’s ratio is 0.3, and density is 7850 kg/m3. The geometrical parameters of the pipeline are 5000 mm vertical pipe, 3000 mm horizontal pipe, 500 mm radius of bend, and 50 mm nominal diameter. The inside of the pipeline is natural gas, which is 0.668 kg/m3 and the dynamic viscosity is 1.087×10-5 Pa·s under standard conditions. The boundary condition is that the fluid inlet velocity is 5 m/s and the outlet is the atmosphere, so it is set as a free-flowing state. The unstructured tetrahedral elements of the pipeline are automatically meshed, as shown in Fig. 3. The horizontal pipe is set to fixed support (Fixed Support), and the stand pipe is in an unconstrained state, as shown in Fig. 4.
Fig. 3Mesh model

Fig. 4Constraint model

3. Calculation results
3.1. Modal calculation results
As shown in Fig. 3, the natural frequency is calculated for the model under uncoupling and fluid-solid coupling (gas-solid coupling) working conditions. The first 6-order amplitude (unit: mm) of the pipeline under uncoupling and fluid-structure coupling conditions are shown in Fig. 5 and Fig. 6; the first 12-order natural frequencies of the two working conditions are shown in Table 1.
Fig. 5The first 6-order amplitude of no coupling pipeline
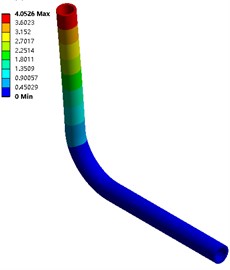
a) Order one
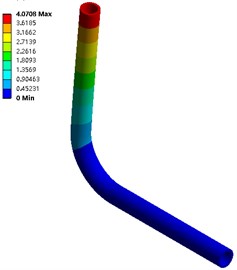
b) Order two
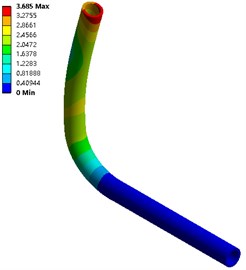
c) Order three
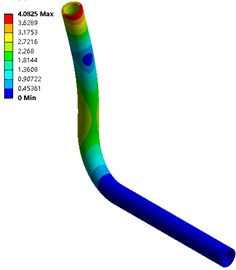
d) Order four
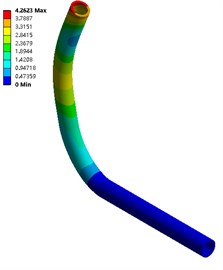
e) Order five
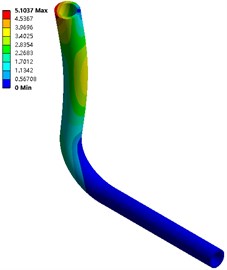
f) Order six
From Fig. 5 and Fig. 6, in the two calculation methods, the vibration pattern under the same vibration order is roughly the same, and the amplitude distribution position is basically the same: the first three orders of amplitude are concentrated at the pipe outlet, and the law is from top to bottom The amplitude is reduced, and the amplitude under fluid-solid coupling conditions is slightly larger than that without coupling, with a maximum value of 4.053 mm; the middle of the third-order pipeline even near the elbow position also has a larger amplitude.
Fig. 6The first 6-order amplitude of the pipeline under fluid-solid coupling conditions
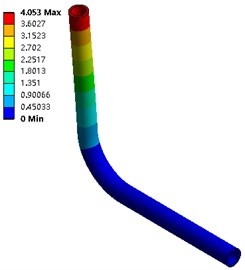
a) Order one

b) Order two

c) Order three

d) Order four
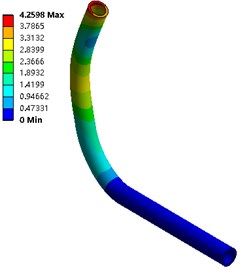
e) Order five
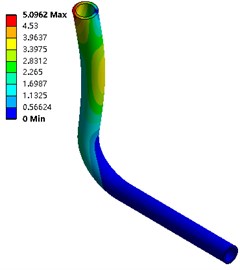
f) Order six
It can be seen from Table 1 and Fig. 7 that natural gas has an impact on the natural frequency of the pipeline. The difference between the natural frequency of the pipeline under the conditions of non-fluid-structure coupling and fluid-structure coupling is up to 9.6 %, and the natural frequency of the pipeline under fluid-structure coupling conditions is slightly higher than that of no coupling. Natural frequency under working conditions.
Table 1Natural frequency of pipeline
Order | No coupling frequency / Hz | Fluid-structure coupling / Hz |
1 | 31.765 | 31.859 |
2 | 32.399 | 33.363 |
3 | 171.270 | 173.370 |
4 | 182.200 | 182.320 |
5 | 330.360 | 330.421 |
6 | 354.160 | 354.223 |
7 | 497.240 | 498.782 |
8 | 720.950 | 721.368 |
9 | 851.340 | 931.740 |
10 | 1157.600 | 1175.756 |
11 | 1165.400 | 1165.365 |
12 | 1280.600 | 1281.156 |
Fig. 7The first 12 natural frequencies of no coupling and fluid-structure coupling
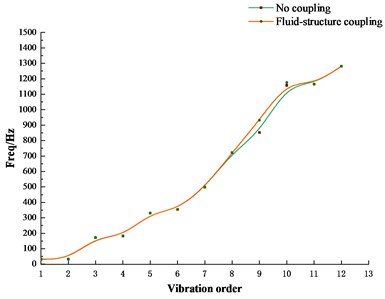
3.2. Calculation results of transient structure
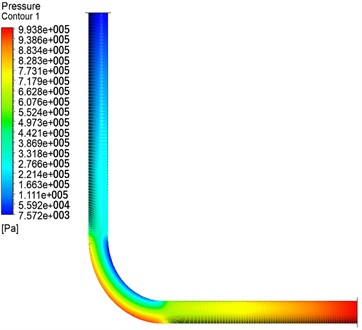
Use the Transient Structural module of ANSYS-Workbench to analyze the flow rate and pressure of the fluid in the pipeline. From Fig. 8, the maximum velocity appears at the elbow, and the inner diameter fluid velocity is greater than the outer diameter fluid velocity; this phenomenon is the opposite in the riser. From Bernoulli’s principle, it can be known that where the flow velocity is large, the pressure is small, and where the flow velocity is small, the pressure is strong. This conclusion can be verified by the calculation result of the fluid pressure distribution in the pipeline in Fig. 9.
Fig. 8Velocity streamline diagram

Fig. 9Fluid pressure distribution diagram in the pipeline
4. Cause analysis of pipeline vibration and structural improvement
4.1. Low pipe stiffness
From the calculation results of the first three-order amplitude in Section 2.1, it can be seen that the riser is in a free and unconstrained state, and its height is high, and the rigidity is insufficient, which makes the amplitude larger.
4.2. Air flow pulsation in the pipe
Air pulsation usually occurs at cross-sectional changes. For example, the curve in this article will generate pulsating force due to air pulsation, as shown in Section 2.2 of this article. However, air pulsation always exists, and pipeline vibration cannot be completely eliminated. Only scientific methods can be used to reduce air pulsation and make it smaller than the engineering allowable value.
4.3. Improvement of pipeline structure
Installing an orifice plate of appropriate size at the inlet or outlet of the large container in the pipeline can form a non-reflective end, which converts the standing wave existing in the pipeline into a traveling wave, thereby reducing pressure pulsation. The hole size can be determined by the following formula (As shown in Fig. 10):
where, is the aperture, mm; tube inner diameter; is average flow velocity; is corresponds to the sound velocity at the average temperature, m/s.
Fig. 10Axial section view of orifice plate
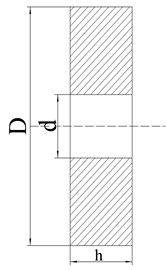
Fig. 11Improved pipeline
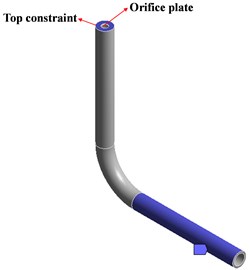
In summary 3.1 chapter and 3.2 chapter, the structure of the pipeline is now improved: for the large amplitude caused by the lower stiffness of the riser, consider installing support for the nozzle; for the pulsation force caused by the pulsation of the pipeline airflow, consider adding holes for the pipeline The plate is used to reduce air pulsation. The orifice plate is installed at the inlet or outlet of the large container in the pipeline. The orifice plate parameter is 30 % of the pipe's nominal diameter. It has a single hole and the plate hole is installed at the riser mouth, as shown in Fig. 11. In this paper, the finite element calculation of the improved pipeline is carried out, and the results are compared with those before the improvement.
5. Comparative analysis
5.1. Maximum amplitude
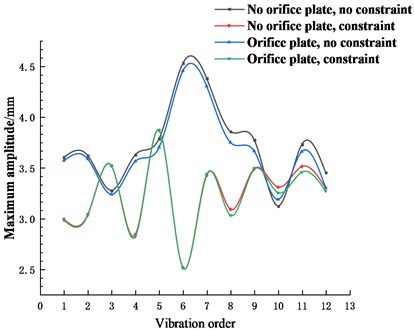
The variation curve of the maximum amplitude of each order of the pipeline with the pipeline structure under the fluid-solid coupling condition is shown in Fig. 12. It can be seen from Fig. 12 that the amplitude variation law of the unconstrained plate with orifice is similar to that of the unconstrained plate with orifice, and the amplitude of the pipe with orifice plate is slightly smaller than that of the plate without orifice; Similar, and the amplitude of the constrained pipe with a perforated plate is slightly smaller than that of the constrained pipe without a perforated plate; and the amplitude of the constrained pipe is smaller than that of the pipe without top constrain.
Fig. 12Variation curve of the maximum amplitude of each order with the pipeline structure
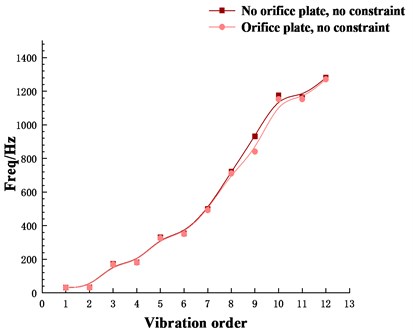
5.2. Each order’s natural frequencies
The change curve of the natural frequency of each order of the pipeline with or without the orifice structure is shown in Fig. 13. It can be seen from Fig. 13 that the natural frequencies of the two structures are similar in each order under fluid-structure coupling conditions, and both increase nonlinearly with the increase of the order, and the natural frequency of the pipe with orifice is lower than that without orifice.
Fig. 13Curves of natural frequencies varying with structure
6. Conclusions
The maximum amplitude of natural gas pipeline under fluid-solid coupling and uncoupling conditions is mainly concentrated at the nozzle in the low-order mode, and the maximum amplitude of the former is slightly higher than that of the latter. Through the transient analysis of the pipeline, it is found that the inner diameter flow rate is large and the pressure is small at the pipe bends, and the outer diameter flow rate is small and the pressure is high; the pulsation force will be generated at the cross section change, which is the exciting force that causes the pipeline to vibrate.
The finite element software is used to analyze the improved structure of the pipeline, and the results are compared with the results before the improvement. It is found that the top constraint has a significant effect on reducing the maximum amplitude of each order of the pipeline; the orifice plate can eliminate the air flow pulsation to reduce the pipeline amplitude. On the whole, the maximum amplitude of the perforated plate and the top constrained pipeline is the smallest, which shows that the structural improvement of the pipeline is reasonable.
References
-
Li Y. T. et al., “Comparison analysis on the scheduled venting modes of gas pipelines,” (in Chinese), Oil and Gas Storage and Transportation, Vol. 38, pp. 429–434, 2019.
-
Lv P. B. et al., “Fast-assembling nitrogen injection device for hot work of pipeline in station,” (in Chinese), Oil and Gas Storage and Transportation, Vol. 39, pp. 1197–1200, 2020.
-
Bie H. Y. and Hao Z. R., “Studies on the jet noise characteristics in different environments,” (in Chinese), Journal of Engineering Thermo-physics, Vol. 36, pp. 1687–1690, 2015.
-
Zhang K., “Calculating venting time of gas pipelines and operation control methods,” (in Chinese), Natural Gas Technology and Economy, Vol. 15, pp. 27–32, 2021.
-
Cen K. et al., “Ignition characteristics of ground deflagration ignition device for vent flares,” Chemical Engineering of Oil and Gas, Vol. 49, pp. 117–124, 2020, https://doi.org/10.3969/j.issn.1007-3426.2020.06.020
-
Zhang Y. et al., “Practice and thought on venting of China-Myanmar Natural Gas Pipeline,” (in Chinese), Oil and Gas Storage and Transportation, Vol. 40, pp. 313–318, 2021.
-
Li L. D. et al., “Selection of venting method for long distance natural gas pipeline,” (in Chinese), Oil and Gas Storage and Transportation, Vol. 40, No. 1, pp. 71–77, 2021.
-
Feng S. and Cai Y. Q., “Simulation on venting and pressure-relieving rules of long distance subsea natural gas pipelines,” (in Chinese), Oil and Gas Storage and Transportation, Vol. 37, No. 3, pp. 328–335, 2018.
-
C. Kalliontzis, E. Andrianis, K. Spyropoulos, and S. Doikas, “Nonlinear static stress analysis of submarine high pressure pipelines,” Computers and Structures, Vol. 63, No. 3, pp. 397–411, May 1997, https://doi.org/10.1016/s0045-7949(96)00371-9
-
Y. S. Hamed, K. M. Albogamy, and M. Sayed, “Nonlinear vibrations control of a contact-mode AFM model via a time-delayed positive position feedback,” Alexandria Engineering Journal, Vol. 60, No. 1, pp. 963–977, Feb. 2021, https://doi.org/10.1016/j.aej.2020.10.024
-
M. Sayed, A. A. Mousa, and I. Mustafa, “Stability and bifurcation analysis of a buckled beam via active control,” Applied Mathematical Modelling, Vol. 82, pp. 649–665, Jun. 2020, https://doi.org/10.1016/j.apm.2020.01.074
-
A. Kandil, M. Sayed, and N. A. Saeed, “On the nonlinear dynamics of constant stiffness coefficients 16-pole rotor active magnetic bearings system,” European Journal of Mechanics – A/Solids, Vol. 84, p. 104051, Nov. 2020, https://doi.org/10.1016/j.euromechsol.2020.104051
-
N. A. Saeed, S. I. El-Bendary, M. Sayed, M. S. Mohamed, and S. K. Elagan, “On the oscillatory behaviours and rub-impact forces of a horizontally supported asymmetric rotor system under position-velocity feedback controller,” Latin American Journal of Solids and Structures, Vol. 18, No. 2, pp. 1–28, 2021, https://doi.org/10.1590/1679-78256410
-
A. A. Mousa, M. Sayed, I. M. Eldesoky, and W. Zhang, “Nonlinear stability analysis of a composite laminated piezoelectric rectangular plate with multi-parametric and external excitations,” International Journal of Dynamics and Control, Vol. 2, No. 4, pp. 494–508, Dec. 2014, https://doi.org/10.1007/s40435-014-0057-x
-
Y. S. Hamed, K. M. Albogamy, and M. Sayed, “A proportional derivative (PD) Controller for suppression the vibrations of a contact-mode AFM model,” IEEE Access, Vol. 8, pp. 214061–214070, 2020, https://doi.org/10.1109/access.2020.3038150
-
M. Sayed and A. A. Mousa, “Vibration, stability, and resonance of angle-ply composite laminated rectangular thin plate under Multiexcitations,” Mathematical Problems in Engineering, Vol. 2013, pp. 1–26, 2013, https://doi.org/10.1155/2013/418374
