Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix

Tang, Dong; Yao, Xiongliang; Wu, Guoxun

doi:10.21595/jve.2016.16950

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2016

Check for updates

Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix

Dong Tang¹

Xiongliang Yao²

Guoxun Wu³

^{1, 2, 3}College of Shipbuilding Engineering, Harbin Engineering University, Harbin, 150001, China

Corresponding Author:

Dong Tang

Cite the article Download PDF

Downloads 1666

WoS Core Citations 5

CrossRef Citations 6

Abstract

This paper is concerned with free vibration analysis of plate/shell coupled structures with two opposite edges simply supported by the method of reverberation-ray matrix. The equations of motion of the flat plate and the open circular cylindrical shell, respectively based on the classical thin plate theory and the Flügge thin shell theory, are introduced. Analytical solutions of the combination of a traveling wave form along the circumferential direction and a standing wave form along the axial direction are obtained. The method of reverberation-ray matrix is applied to derive the equation of the natural frequencies for the plate/shell coupled structures. The semi-analytical natural frequencies are obtained with the employment of the golden section search algorithm. The semi-analytical calculation results of three typical plate/shell coupled structures are presented and the results are compared with those obtained by the finite element method. The comparison shows that the calculation results obtained in this paper are of high accuracy and that the formulation presented in this manuscript are validated for free vibration analysis of plate/shell coupled structures.

1. Introduction

Thin plates and thin shells are extensively used in civil, mechanical and aeronautical engineering as well as in naval architecture and ocean engineering. Most of the practical engineering structures, such as the fuselages of aircraft, the ship hulls and the ocean platforms, etc., involve plate/shell coupled structures. The vibration behaviors of such coupled structures attract much attention from engineers in their practical designs. Quite a few experimental and analytical studies have been conducted on vibration analysis of plates and shells, but not so many researches are concerned with the plate/shell coupled structures.

Vibration of coupled structures with plate components has been studied by many researchers in the past decades. Vibration behaviors of folded plates are analyzed in literature [1-9]. Vibration characteristics of and power flow transmission through the L-shaped plate are studied in [10-20]. Vibration behaviors of box-type structures are investigated by a few researchers. Dickinson and Warburton [21] analyzed the free flexural vibrations of open and closed rectangular boxes and presented a theoretical solution using a sine series. Popplewell [22] studied the free vibration of a box-type structure and the natural frequencies and normal modes are presented. Handa [23] analyzed the in-plane vibration of box-type structures by a finite element method. By considering the spatial properties of distributed forces in terms of their Fourier components and hypothesizing that the uniform component is dominant, Fulford and Petersson [24, 25] accounted for the spatially distributed wavefield at the connections of the built-up structures and the vibratory power for the box-like structure supported by an infinite plate-like recipient were considered. Lee and Wooh [26] presented the free vibration analysis of folded structures and box beams made of composite materials using a four-noded Lagrangian and Hermite finite element that incorporates high order transverse shear deformation and rotary inertia and the significance of the high order plate theory in analyzing folded structures is enunciated. Lin and Pan studied the vibration characteristics of a box-type structure using the finite element method [27], and subsequently investigated the sound radiation characteristics of a box-type structure with the employment of the finite element and boundary element methods [28]. More recently, Chen et al. [29] developed an analytical approach to investigate the vibration behaviors of a box-type built-up structure and energy transmission through the structure.

Most of the available researches on plate/shell coupled structures are concerned with closed circular cylindrical shells with end plates. Yamada et al. [30] presented the free vibration analysis of a circular cylindrical double-shell system closed by end plates. Schlesinger [31] investigated the transmission of elastic waves from a cylinder to an attached flat plate with the wave approach. Tso and Hansen [32] also studied the transmission of vibration waves through cylinder/plate junctions. Stanley and Ganesan [33] determined the natural frequencies of cylindrical shells with a circular plate attached at arbitrary locations for various boundary conditions using the semi-analytical finite element method. Tso and Hansen [34] presented a theoretical and experimental study of the transmission of vibration through a two element structure which consists of a cylindrical shell coupled to an end plate. Wu et al. [35] analyzed the vibroacoustic coupling between a finite circular cylindrical shell closed at each end by a piece of circular plate and its enclosed cavity by using the covering-domain method, which transforms the calculation of the scattering sound field of a complicated-shaped close cavity to that of a series of simply regular-shaped close shells. Wang et al. [36] formulated a substructure approach to investigate the power flow characteristics of a plate-cylindrical shell system subject to both conservative and dissipative coupling conditions. Liang and Chen [37] investigated the natural frequencies and mode shapes for a conical shell with an annular end plate or a round end plate by means of the transfer matrix method. Subsequently, Liang et al. [38] extended the transfer matrix method to analyze a composite laminated conical-plate shell. Recently, much attentions are paid to vibration analysis of joined cylindrical, conical or spherical shells [39-50].

This paper presents an analytical formulation for the free vibration analysis of plate/shell coupled structures with two opposite edges simply supported. Firstly, the force and moment resultants in a thin plate and in an open circular cylindrical shell (OCCS) are presented and the equations of motion of the thin plate and the OCCS, respectively based on the classical thin plate theory and the Flügge thin shell theory, are introduced. Then, analytical solutions of the combination of a traveling wave form along the circumferential direction and a standing wave form along the axial direction are obtained for both of the thin plate and the OCCS with two opposite edges simply supported. Subsequently, the method of reverberation-ray matrix (MRRM) is employed to derive the equation of natural frequencies for plate/shell coupled structures and the golden section search algorithm is applied to find the semi-analytical natural frequencies of the plate/shell coupled structures. Finally, the calculation results of three typical plate/shell coupled structures are presented and the results are compared with those obtained by the finite element method.

2. Formulation

According to the classical thin plate theory and the Flügge thin shell theory, the force and moment resultants and the governing differential equations for the basic components of the plate/shell coupled structures are presented at the beginning of this section. Analytical solutions of the combination form of a traveling wave along one direction and a standing wave along the other direction are obtained for both of the thin plate and the OCCS with two opposite edges simply supported. After that, the displacements and the force and moment resultants are expressed in matrix form to derive the scattering matrix, the phase matrix and the permutation matrix, which are subsequently used to formulate the reverberation-ray matrix and to obtain the equation of natural frequencies of the plate/shell coupled structures. Finally, the golden section search algorithm is applied to find the natural frequencies of the plate/shell coupled structures.

2.1. Force and moment resultants in a plate

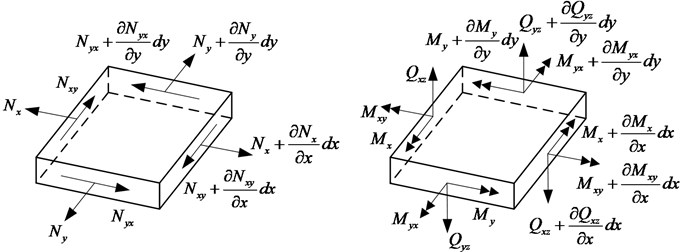
The force and moment resultants in a thin plate are shown in Fig. 1, in which the positive directions are indicated. Based on the generalized Hooke’s law, the strain-displacement relations and the stress-strain relations of the element of the thin plate, the force and moment resultants in the plate can be expressed in terms of the in-plane longitudinal, in-plane shear and out-plane displacements as follows:

1

N_{x} = C (\frac{\partial u}{\partial x} + \frac{μ \partial v}{\partial y}),

2

N_{y} = C (\frac{\partial v}{\partial y} + \frac{μ \partial u}{\partial x}),

3

N_{x y} = N_{y x} = \frac{C (\partial u / \partial y + \partial v / \partial x) (1 - μ)}{2},

4

M_{x} = - D (\frac{\partial^{2} w}{\partial x^{2}} + \frac{μ \partial^{2} w}{\partial y^{2}}),

5

M_{y} = - D (\frac{\partial^{2} w}{\partial y^{2}} + \frac{μ \partial^{2} w}{\partial x^{2}}),

6

M_{x y} = M_{y x} = - \frac{D (1 - μ) \partial^{2} w}{\partial x \partial y},

7

Q_{x z} = - D (\frac{\partial^{3} w}{\partial x^{3}} + \frac{\partial^{3} w}{\partial x \partial y^{2}}),

8

Q_{y z} = - D (\frac{\partial^{3} w}{\partial y^{3}} + \frac{\partial^{3} w}{\partial x^{2} \partial y}),

9

V_{x z} = - D [\frac{\partial^{3} w}{\partial x^{3}} + \frac{(2 - μ) \partial^{3} w}{\partial x \partial y^{2}}],

10

V_{y z} = - D [\frac{\partial^{3} w}{\partial y^{3}} + \frac{(2 - μ) \partial^{3} w}{\partial x^{2} \partial y}],

where $u$ , $v$ and $w$ denote the in-plane longitudinal, in-plane shear and out-plane displacements along $x$ , $y$ and $z$ directions, respectively. $C = E h / (1 - μ^{2})$ and $D = E h^{3} / 12 (1 - μ^{2})$ are the membrane stiffness and the bending stiffness of the plate, where $E$ is Young’s modulus, $μ$ is Poisson’s ratio, and $h$ is the thickness of the plate. $N_{x}$ and $N_{y}$ denote the in-plane normal forces, $N_{x y}$ and $N_{y x}$ , the in-plane shear forces, $M_{x}$ and $M_{y}$ , the bending moment, $M_{x y}$ and $M_{y x}$ , the torsional moment, and $Q_{x z}$ and $Q_{y z}$ , the out-plane shear forces, $V_{x z}$ and $V_{y z}$ , represent the Kirchhoff effective shear force resultants of the first kind acting on the cross-sections perpendicular to the $x$ and $y$ directions, respectively.

Fig. 1Force and moment resultants in a thin plate

2.2. Governing differential equations and the solutions of the plate

According to the dynamic equilibrium of forces in the $x$ , $y$ and $z$ directions and the relations of the force and moment resultants with the displacements defined by Eqs. (1)-(10), the governing differential equations for the free vibration of a thin plate are obtained as follows:

11

\frac{\partial^{2} u}{\partial x^{2}} + \frac{1 - μ}{2} \frac{\partial^{2} u}{\partial y^{2}} + \frac{1 + μ}{2} \frac{\partial^{2} v}{\partial x \partial y} - \frac{(1 - μ^{2}) ρ}{E} \frac{\partial^{2} u}{\partial t^{2}} = 0,

12

\frac{\partial^{2} v}{\partial y^{2}} + \frac{1 - μ}{2} \frac{\partial^{2} v}{\partial x^{2}} + \frac{1 + μ}{2} \frac{\partial^{2} u}{\partial x \partial y} - \frac{(1 - μ^{2}) ρ}{E} \frac{\partial^{2} v}{\partial t^{2}} = 0,

13

D \nabla^{4} w + ρ h \frac{\partial^{2} w}{\partial t^{2}} = 0,

where $ρ$ is the mass density of the plate.

Taking the Fourier transforms of Eqs. (11)-(13), the governing differential equations can be expressed in the frequency domain as:

14

\frac{\partial^{2} \tilde{u}}{\partial x^{2}} + \frac{1 - μ}{2} \frac{\partial^{2} \tilde{u}}{\partial y^{2}} + \frac{1 + μ}{2} \frac{\partial^{2} \tilde{v}}{\partial x \partial y} + k_{L}^{2} \tilde{u} = 0,

15

\frac{\partial^{2} \tilde{v}}{\partial y^{2}} + \frac{1 - μ}{2} \frac{\partial^{2} \tilde{v}}{\partial x^{2}} + \frac{1 + μ}{2} \frac{\partial^{2} \tilde{u}}{\partial x \partial y} + k_{L}^{2} \tilde{v} = 0,

16

D \nabla^{4} \tilde{w} - ρ h ω^{2} \tilde{w} = 0,

where a tide over a symbol represents the corresponding physical quantity in the frequency domain, $k_{L} = ω {[(1 - μ^{2}) ρ / E]}^{1 / 2}$ denotes the in-plane longitudinal wave number of the thin plate, and $ω$ is the circular frequency.

With respect to a thin plate simply supported at $x =$ 0 and $x = L_{x}$ , the in-plane longitudinal, in-plane shear, and out-plane displacements can be expressed as the series summation of the products of the modal waves along $x$ direction and the traveling waves along $y$ direction [51]:

17

\tilde{u} (x, y) = \sum_{m = 1}^{\infty} (k_{x} a_{3} e^{k_{y 3} y} + k_{x} d_{3} e^{{- k}_{y 3} y} + k_{y 4} a_{4} e^{k_{y 4} y} + k_{y 4} d_{4} e^{{- k}_{y 4} y}) \cos (k_{x} x),

18

\tilde{v} (x, y) = \sum_{m = 1}^{\infty} (k_{y 3} a_{3} e^{k_{y 3} y} - k_{y 3} d_{3} e^{{- k}_{y 3} y} + k_{x} a_{4} e^{k_{y 4} y} - k_{x} d_{4} e^{{- k}_{y 4} y}) \sin (k_{x} x),

19

\tilde{w} (x, y) = \sum_{m = 1}^{\infty} (a_{1} e^{k_{y 1} y} + d_{1} e^{{- k}_{y 1} y} + a_{2} e^{k_{y 2} y} + d_{2} e^{{- k}_{y 2} y}) \sin (k_{x} x),

where $k_{x} = m π / L_{x}$ denotes the wave number in the $x$ direction, $m$ is the mode number and $L_{x}$ represents the length of the plate. $k_{y 1} = {(k_{x}^{2} - k_{F}^{2})}^{1 / 2}$ and $k_{y 2} = {(k_{x}^{2} + k_{F}^{2})}^{1 / 2}$ are respectively the wave numbers along the $y$ direction for the propagating and evanescent waves corresponding to the out-plane displacement. $k_{y 3} = {(k_{x}^{2} - k_{L}^{2})}^{1 / 2}$ and $k_{y 4} = {(k_{x}^{2} - k_{S}^{2})}^{1 / 2}$ are respectively the wave numbers along the $y$ direction for the propagating waves corresponding to the in-plane displacements. $k_{F} = {(ω^{2} ρ h / D)}^{1 / 4}$ is the in vacuo flexural wave number of the plate. $k_{S} = ω {[2 (1 + μ) ρ / E]}^{1 / 2}$ denotes the in-plane shear wave number. Wave amplitudes corresponding to the arriving wave and the departing wave are respectively indicated by $a_{i}$ and $d_{i}$ ( $i =$ 1-4), in which ( $i =$ 1, 2) for flexural waves of the out-plane displacement and ( $i =$ 3, 4) for longitudinal waves and shear waves of the in-plane displacements.

The rotation of the normal to the mid-plane of the plate about the $x$ direction is defined as:

20

φ_{y} = - \frac{\partial w}{\partial y} .

According to Eq. (19), the above-mentioned rotation can be expressed in frequency domain as:

21

{\tilde{φ}}_{y} (x, y) = \sum_{m = 1}^{\infty} (- k_{y 1} a_{1} e^{k_{y 1} y} + k_{y 1} d_{1} e^{- k_{y 1} y} - k_{y 2} a_{2} e^{k_{y 2} y} + k_{y 2} d_{2} e^{- k_{y 2} y}) \sin (k_{x} x) .

Substituting Eqs. (17)-19) into the Fourier transforms of Eqs. (2), (3), (5) and (10) yields the frequency domain expressions of the force and moment resultants of the plate:

22

{\tilde{N}}_{y} = C \sum_{m = 1}^{\infty} [\begin{matrix} (k_{y 3}^{2} - μ k_{x}^{2}) (a_{3} e^{k_{y 3} y} + d_{3} e^{{- k}_{y 3} y}) \\ + (1 - μ) k_{x} k_{y 4} (a_{4} e^{k_{y 4} y} + d_{4} e^{{- k}_{y 4} y}) \end{matrix}] \sin (k_{x} x),

23

{\tilde{N}}_{y x} = \frac{1 - μ}{2} C \sum_{m = 1}^{\infty} [\begin{matrix} 2 k_{x} k_{y 3} (a_{3} e^{k_{y 3} y} - d_{3} e^{{- k}_{y 3} y}) \\ + (k_{x}^{2} + k_{y 4}^{2}) (a_{4} e^{k_{y 4} y} - d_{4} e^{{- k}_{y 4} y}) \end{matrix}] \cos (k_{x} x),

24

{\tilde{M}}_{y} = - D \sum_{m = 1}^{\infty} [\begin{matrix} (k_{y 1}^{2} - μ k_{x}^{2}) (a_{1} e^{k_{y 1} y} + d_{1} e^{{- k}_{y 1} y}) \\ + (k_{y 2}^{2} - μ k_{x}^{2}) (a_{2} e^{k_{y 2} y} + d_{2} e^{{- k}_{y 2} y}) \end{matrix}] \sin (k_{x} x),

25

{\tilde{V}}_{y z} = - D \sum_{m = 1}^{\infty} \{\begin{matrix} [k_{y 1}^{3} - (2 - μ) k_{y 1} k_{x}^{2}] (a_{1} e^{k_{y 1} y} - d_{1} e^{{- k}_{y 1} y}) \\ + [k_{y 2}^{3} - (2 - μ) k_{y 2} k_{x}^{2}] (a_{2} e^{k_{y 2} y} - d_{2} e^{{- k}_{y 2} y}) \end{matrix}\} \sin (k_{x} x) .

For an arbitrary axial mode number $m$ , Eqs. (17)-(19) and (21) can be expressed in matrix form as:

26

W_{d} = H_{m} (x) W_{d}^{*},

where $W_{d}$ denotes the displacement vector of the plate, $H_{m} (x)$ indicates the axial mode matrix, and $W_{d}^{*}$ represents the vector of the traveling wave solutions corresponding to the displacement vector. They are presented in detail as follows:

27

W_{d} = {\{\tilde{u} \tilde{v} \tilde{w} {\tilde{φ}}_{y}\}}^{T},

28

H_{m} (x) = d i a g \{\cos (k_{x} x) \sin (k_{x} x) \sin (k_{x} x) \sin (k_{x} x)\},

29

W_{d}^{*} = A_{d} P_{h} (- y) a + D_{d} P_{h} (y) d,

in which $A_{d}$ and $D_{d}$ are coefficient matrices, $a$ and $d$ are amplitude vectors corresponding to the arriving wave and the departing wave, respectively. $P_{h} (y)$ represents the phase matrix. They are presented in detail as follows:

30

A_{d} = [\begin{matrix} 0 & 0 & \begin{matrix} k_{x} & k_{y 4} \end{matrix} \\ 0 & 0 & \begin{matrix} k_{y 3} & k_{x} \end{matrix} \\ \begin{matrix} 1 \\ - k_{y 1} \end{matrix} & \begin{matrix} 1 \\ - k_{y 2} \end{matrix} & \begin{matrix} \begin{matrix} 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 \end{matrix} \end{matrix} \end{matrix}], D_{d} = [\begin{matrix} 0 & 0 & \begin{matrix} k_{x} & k_{y 4} \end{matrix} \\ 0 & 0 & \begin{matrix} - k_{y 3} & - k_{x} \end{matrix} \\ \begin{matrix} 1 \\ k_{y 1} \end{matrix} & \begin{matrix} 1 \\ k_{y 2} \end{matrix} & \begin{matrix} \begin{matrix} 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 \end{matrix} \end{matrix} \end{matrix}],

31

P_{h} (y) = d i a g \{e^{- k_{y 1} y} e^{- k_{y 2} y} e^{- k_{y 3} y} e^{- k_{y 4} y}\},

32

a = {\{a_{1} a_{2} a_{3} a_{4}\}}^{T},

33

d = {\{d_{1} d_{2} d_{3} d_{4}\}}^{T} .

Similarly, for an arbitrary axial mode number $m$ , Eqs. (22)-(25) can be expressed in matrix form as:

34

W_{f} = H_{m} (x) W_{f}^{*},

where the physical significance and expression of $H_{m} (x)$ are the same as those presented in Eq. (28). $W_{f}$ denotes the force vector of the plate, and $W_{f}^{*}$ represents the vector of the wave solutions corresponding to the force vector. They are presented in detail as follows:

35

W_{f} = {\{{\tilde{N}}_{y x} {\tilde{N}}_{y} {\tilde{V}}_{y z} {\tilde{M}}_{y}\}}^{T},

36

W_{f}^{*} = A_{f} P_{h} (- y) a + D_{f} P_{h} (y) d,

in which the physical significances and expressions of $P_{h} (y)$ , $a$ and $d$ are the same as those defined in Eq. (29). $A_{f}$ and $D_{f}$ are coefficient matrices corresponding to the arriving wave and the departing wave of the force and moment resultants of the plate. They are presented in detail as follows:

37

A_{f} = [\begin{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} 2 μ_{2} C k_{x} k_{y 3} & μ_{2} C (k_{x}^{2} + k_{y 4}^{2}) \\ C (k_{y 3}^{2} - μ k_{x}^{2}) & 2 μ_{2} C k_{x} k_{y 4} \end{matrix} \\ \begin{matrix} D k_{y 1} [\begin{matrix} (2 - μ) k_{x}^{2} \\ - k_{y 1}^{2} \end{matrix}] & D k_{y 2} [\begin{matrix} (2 - μ) k_{x}^{2} \\ - k_{y 2}^{2} \end{matrix}] \\ D ({μ k_{x}^{2} - k}_{y 1}^{2}) & D (μ k_{x}^{2} - k_{y 2}^{2}) \end{matrix} & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \end{matrix}],

38

D_{f} = [\begin{matrix} \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} - 2 μ_{2} C k_{x} k_{y 3} & {- μ}_{2} C (k_{x}^{2} + k_{y 4}^{2}) \\ C (k_{y 3}^{2} - μ k_{x}^{2}) & 2 μ_{2} C k_{x} k_{y 4} \end{matrix} \\ \begin{matrix} D k_{y 1} [\begin{matrix} (μ - 2) k_{x}^{2} \\ + k_{y 1}^{2} \end{matrix}] & D k_{y 2} [\begin{matrix} (μ - 2) k_{x}^{2} \\ + k_{y 2}^{2} \end{matrix}] \\ D ({μ k_{x}^{2} - k}_{y 1}^{2}) & D (μ k_{x}^{2} - k_{y 2}^{2}) \end{matrix} & \begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix} \end{matrix}],

where $μ_{2}$ is a non-dimensional parameter presented in Appendix A.1.

2.3. Force and moment resultants in an open circular cylindrical shell

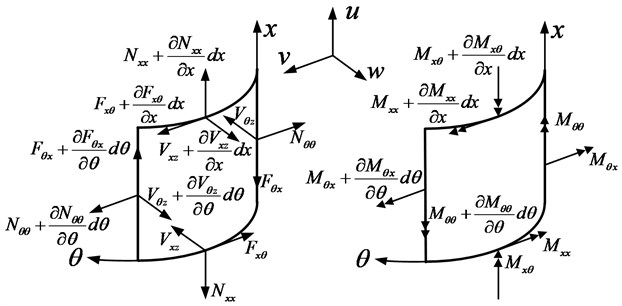
The force and moment resultants in an OCCS are shown in Fig. 2, in which the positive directions are indicated. Based on the Flügge thin shell theory, the force and moment resultants in the OCCS can be expressed in terms of the axial, circumferential and radial displacements as follows:

39

N_{x} = C (\frac{\partial u}{\partial x} + μ \frac{1}{R} \frac{\partial v}{\partial θ} - λ R \frac{\partial^{2} w}{\partial x^{2}} + μ \frac{1}{R} w),

40

N_{θ} = C (μ \frac{\partial u}{\partial x} + \frac{1}{R} \frac{\partial v}{\partial θ} + λ \frac{1}{R} \frac{\partial^{2} w}{\partial θ^{2}} + λ_{1} \frac{1}{R} w),

41

N_{x θ} = μ_{2} C (\frac{1}{R} \frac{\partial u}{\partial θ} + λ_{1} \frac{\partial v}{\partial x} - λ \frac{\partial^{2} w}{\partial x \partial θ}),

42

N_{θ x} = μ_{2} C (λ_{1} \frac{1}{R} \frac{\partial u}{\partial θ} + \frac{\partial v}{\partial x} + λ \frac{\partial^{2} w}{\partial x \partial θ}),

43

M_{x} = D (\frac{1}{R} \frac{\partial u}{\partial x} + μ \frac{1}{R^{2}} \frac{\partial v}{\partial θ} - \frac{\partial^{2} w}{\partial x^{2}} - μ \frac{1}{R^{2}} \frac{\partial^{2} w}{\partial θ^{2}}),

44

M_{θ} = - D (μ \frac{\partial^{2} w}{\partial x^{2}} + \frac{1}{R^{2}} \frac{\partial^{2} w}{\partial θ^{2}} + \frac{1}{R^{2}} w),

45

M_{x θ} = 2 μ_{2} D (\frac{1}{R} \frac{\partial v}{\partial x} - \frac{1}{R} \frac{\partial^{2} w}{\partial x \partial θ}),

46

M_{θ x} = {- μ}_{2} D (\frac{1}{R^{2}} \frac{\partial u}{\partial θ} - \frac{1}{R} \frac{\partial v}{\partial x} + 2 \frac{1}{R} \frac{\partial^{2} w}{\partial x \partial θ}),

47

Q_{x z} = D (\frac{1}{R} \frac{\partial^{2} u}{\partial x^{2}} - μ_{2} \frac{1}{R^{3}} \frac{\partial^{2} u}{\partial θ^{2}} + μ_{1} \frac{1}{R^{2}} \frac{\partial^{2} v}{\partial x \partial θ} - \frac{\partial^{3} w}{\partial x^{3}} - \frac{1}{R^{2}} \frac{\partial^{3} w}{\partial x \partial θ^{2}}),

48

Q_{θ z} = D (2 μ_{2} \frac{1}{R} \frac{\partial^{2} v}{\partial x^{2}} - \frac{1}{R} \frac{\partial^{3} w}{\partial x^{2} \partial θ} - \frac{1}{R^{3}} \frac{\partial^{3} w}{\partial θ^{3}} - \frac{1}{R^{3}} \frac{\partial w}{\partial θ}),

49

F_{x θ} = μ_{2} C (\frac{1}{R} \frac{\partial u}{\partial θ} + λ_{2} \frac{\partial v}{\partial x} - 3 λ \frac{\partial^{2} w}{\partial x \partial θ}),

50

F_{θ x} = μ_{2} C (λ_{1} \frac{1}{R} \frac{\partial u}{\partial θ} + \frac{\partial v}{\partial x} + λ \frac{\partial^{2} w}{\partial x \partial θ}),

51

V_{x z} = D [\frac{1}{R} \frac{\partial^{2} u}{\partial x^{2}} - μ_{2} \frac{1}{R^{3}} \frac{\partial^{2} u}{\partial θ^{2}} + μ_{3} \frac{1}{R^{2}} \frac{\partial^{2} v}{\partial x \partial θ} - \frac{\partial^{3} w}{\partial x^{3}} - (2 - μ) \frac{1}{R^{2}} \frac{\partial^{3} w}{\partial x \partial θ^{2}}],

52

V_{θ z} = - D [μ_{2} \frac{1}{R^{2}} \frac{\partial^{2} u}{\partial x \partial θ} - 3 μ_{2} \frac{1}{R} \frac{\partial^{2} v}{\partial x^{2}} + (2 - μ) \frac{1}{R} \frac{\partial^{3} w}{\partial x^{2} \partial θ} + \frac{1}{R^{3}} \frac{\partial^{3} w}{\partial θ^{3}} + \frac{1}{R^{3}} \frac{\partial w}{\partial θ}],

where $u$ , $v$ and $w$ denote the displacement components in the axial ( $x$ ), circumferential ( $θ$ ), and radial ( $z$ ) directions, respectively. $C = E h / 1 - μ^{2}$ and $D = E h^{3} / 12 (1 - μ^{2})$ are the membrane stiffness and the bending stiffness of the shell, where $E$ is Young’s modulus, $μ$ is Poisson’s ratio, $h$ is the thickness and $R$ is the radius of the shell. $λ = h^{2} / 12 R^{2}$ is a dimensionless parameter, which is related with the ratio of the shell thickness to the shell radius. $λ_{1}$ , $λ_{2}$ , $μ_{1}$ , $μ_{2}$ and $μ_{3}$ are dimensionless parameters presented in Appendix A.1. $N_{x}$ and $N_{θ}$ denote the in-plane normal forces, $N_{x θ}$ and $N_{θ x}$ , the in-plane shear forces, $M_{x}$ and $M_{θ}$ , the bending moment, $M_{x θ}$ and $M_{θ x}$ , the torsional moment, and $Q_{x z}$ and $Q_{θ z}$ , the out-plane shear forces acting on the cross-sections perpendicular to the axial and circumferential directions, respectively. Besides, $V_{x z}$ and $V_{θ z}$ indicate the Kirchhoff effective shear force resultants of the first kind, namely, the in-plane shear force resultants, and $F_{x θ}$ and $F_{θ x}$ , the Kirchhoff effective shear force resultants of the second kind, namely, the out-plane shear force resultants acting on the cross-sections perpendicular to the axial and circumferential directions, respectively.

Fig. 2Force and moment resultants in an open circular cylindrical shell

2.4. Governing differential equations and solutions of the open circular cylindrical shell

The governing differential equations for the free vibration of an OCCS based on the Flügge thin shell theory can be written as:

53

R^{2} \frac{\partial^{2} u}{\partial x^{2}} + μ_{2} λ_{1} \frac{\partial^{2} u}{\partial θ^{2}} + μ_{1} R \frac{\partial^{2} v}{\partial x \partial θ} - λ R^{3} \frac{\partial^{3} w}{\partial x^{3}} + μ_{2} λ R \frac{\partial^{3} w}{\partial x \partial θ^{2}}

+ μ R \frac{\partial w}{\partial x} - R^{2} \frac{(1 - μ^{2}) ρ}{E} \frac{\partial^{2} u}{\partial t^{2}} = 0,

54

μ_{1} R \frac{\partial^{2} u}{\partial x \partial θ} + μ_{2} λ_{2} R^{2} \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial θ^{2}} - μ_{3} λ R^{2} \frac{\partial^{3} w}{\partial x^{2} \partial θ} + \frac{\partial w}{\partial θ} - R^{2} \frac{(1 - μ^{2}) ρ}{E} \frac{\partial^{2} v}{\partial t^{2}} = 0,

55

{- λ R}^{3} \frac{\partial^{3} u}{\partial x^{3}} + μ_{2} λ R \frac{\partial^{3} u}{\partial x \partial θ^{2}} + μ R \frac{\partial u}{\partial x} - μ_{3} λ R^{2} \frac{\partial^{3} v}{\partial x^{2} \partial θ} + \frac{\partial v}{\partial θ} + λ R^{4} \frac{\partial^{4} w}{\partial x^{4}}

+ 2 λ R^{2} \frac{\partial^{4} w}{\partial x^{2} \partial θ^{2}} + λ \frac{\partial^{4} w}{\partial θ^{4}} + 2 λ \frac{\partial^{2} w}{\partial θ^{2}} + λ_{1} w + R^{2} \frac{(1 - μ^{2}) ρ}{E} \frac{\partial^{2} w}{\partial t^{2}} = 0 .

Taking the Fourier transforms of Eqs. (53)-(55), the governing differential equations can be expressed in the frequency domain as:

56

R^{2} \frac{\partial^{2} \tilde{u}}{\partial x^{2}} + μ_{2} λ_{1} \frac{\partial^{2} \tilde{u}}{\partial θ^{2}} + R^{2} k_{L}^{2} \tilde{u} + μ_{1} R \frac{\partial^{2} \tilde{v}}{\partial x \partial θ} - λ R^{3} \frac{\partial^{3} \tilde{w}}{\partial x^{3}} + μ_{2} λ R \frac{\partial^{3} \tilde{w}}{\partial x \partial θ^{2}} + μ R \frac{\partial \tilde{w}}{\partial x} = 0,

57

μ_{1} R \frac{\partial^{2} \tilde{u}}{\partial x \partial θ} + μ_{2} λ_{2} R^{2} \frac{\partial^{2} \tilde{v}}{\partial x^{2}} + \frac{\partial^{2} \tilde{v}}{\partial θ^{2}} + R^{2} k_{L}^{2} \tilde{v} - μ_{3} λ R^{2} \frac{\partial^{3} \tilde{w}}{\partial x^{2} \partial θ} + \frac{\partial \tilde{w}}{\partial θ} = 0,

58

{- λ R}^{3} \frac{\partial^{3} \tilde{u}}{\partial x^{3}} + μ_{2} λ R \frac{\partial^{3} \tilde{u}}{\partial x \partial θ^{2}} + μ R \frac{\partial \tilde{u}}{\partial x} - μ_{3} λ R^{2} \frac{\partial^{3} \tilde{v}}{\partial x^{2} \partial θ} + \frac{\partial \tilde{v}}{\partial θ} + λ R^{4} \frac{\partial^{4} \tilde{w}}{\partial x^{4}}

+ 2 λ R^{2} \frac{\partial^{4} \tilde{w}}{\partial x^{2} \partial θ^{2}} + λ \frac{\partial^{4} \tilde{w}}{\partial θ^{4}} + 2 λ \frac{\partial^{2} \tilde{w}}{\partial θ^{2}} + λ_{1} \tilde{w} - R^{2} k_{L}^{2} \tilde{w} = 0 .

With respect to an OCCS simply supported at $x =$ 0 and $x = L_{x}$ , the axial, circumferential and radial displacements can be expressed as the series summation of the products of the mode waves along the axial direction and the traveling waves along the circumferential direction:

59

\tilde{u} (x, θ) = \sum_{m = 1}^{\infty} (\begin{matrix} α_{1} a_{1} e^{k_{θ 1} θ} + α_{1} d_{1} e^{- k_{θ 1} θ} + α_{2} a_{2} e^{k_{θ 2} θ} + α_{2} d_{2} e^{- k_{θ 2} θ} \\ + α_{3} a_{3} e^{k_{θ 3} θ} + α_{3} d_{3} e^{- k_{θ 3} θ} + α_{4} a_{4} e^{k_{θ 4} θ} + α_{4} d_{4} e^{- k_{θ 4} θ} \end{matrix}) \cos (k_{x} x),

60

\tilde{v} (x, θ) = \sum_{m = 1}^{\infty} (\begin{matrix} β_{1} a_{1} e^{k_{θ 1} θ} - β_{1} d_{1} e^{- k_{θ 1} θ} + β_{2} a_{2} e^{k_{θ 2} θ} - β_{2} d_{2} e^{- k_{θ 2} θ} \\ + β_{3} a_{3} e^{k_{θ 3} θ} - β_{3} d_{3} e^{- k_{θ 3} θ} + β_{4} a_{4} e^{k_{θ 4} θ} - β_{4} d_{4} e^{- k_{θ 4} θ} \end{matrix}) \sin (k_{x} x),

61

\tilde{w} (x, θ) = \sum_{m = 1}^{\infty} (\begin{matrix} a_{1} e^{k_{θ 1} θ} + d_{1} e^{- k_{θ 1} θ} + a_{2} e^{k_{θ 2} θ} + d_{2} e^{- k_{θ 2} θ} \\ + a_{3} e^{k_{θ 3} θ} + d_{3} e^{- k_{θ 3} θ} + a_{4} e^{k_{θ 4} θ} + d_{4} e^{- k_{θ 4} θ} \end{matrix}) \sin (k_{x} x),

where $k_{x} = m π / L_{x}$ denotes the wave number in the x direction, $m$ is the mode number and $L_{x}$ represents the length of the shell. $a_{i}$ and $d_{i}$ ( $i =$ 1-4) represent wave amplitudes corresponding to the arriving wave and the departing wave, respectively. $α_{i}$ and $β_{i}$ ( $i =$ 1-4) are amplitude coefficients of the axial and circumferential waves. The expressions of $α_{i}$ and $β_{i}$ are defined as follows:

62

α_{i} = - \frac{R k_{x} (μ_{2} λ k_{θ i}^{4} - ξ_{10}^{2} k_{θ i}^{2} + ξ_{3}^{2} ξ_{8}^{2})}{(μ_{2} λ_{1} k_{θ i}^{4} + ξ_{1}^{2} k_{θ i}^{2} + ξ_{2}^{2} ξ_{3}^{2})},

63

β_{i} = - \frac{k_{θ i} (ξ_{6}^{2} k_{θ i}^{2} + ξ_{7}^{2} ξ_{8}^{2} + ξ_{2}^{2} ξ_{9}^{2})}{(μ_{2} λ_{1} k_{θ i}^{4} + ξ_{1}^{2} k_{θ i}^{2} + ξ_{2}^{2} ξ_{3}^{2})},

and $k_{θ i}$ ( $i =$ 1-4) are circumferential wave numbers defined by the following equation:

64

(μ_{1} λ_{1} k_{θ}^{4} + ξ_{1}^{2} k_{θ}^{2} + ξ_{2}^{2} ξ_{3}^{2}) (μ_{2} k_{θ}^{4} + ξ_{4}^{2} k_{θ}^{2} + ξ_{5}^{4})

+ \frac{(ξ_{6}^{2} k_{θ}^{2} + ξ_{7}^{2} ξ_{8}^{2} + ξ_{2}^{2} ξ_{9}^{2}) (μ_{1} λ k_{θ}^{4} - ξ_{10}^{2} k_{θ}^{2} + ξ_{3}^{2} ξ_{8}^{2})}{λ} = 0,

where $μ_{i}$ ( $i =$ 1-3), $λ_{i}$ ( $i =$ 1-2) and $ξ_{i}$ ( $i =$ 1-10) are non-dimensional parameters presented in detail in Appendix A1 and Appendix A2.

The rotation of the normal to the mid-surface of the shell about the axial direction is defined as:

65

φ_{θ} = \frac{v}{R} - \frac{\partial w}{R \partial θ} .

According to Eqs. (60) and (61), the above-mentioned rotation can be expressed in frequency domain as:

66

{\tilde{φ}}_{θ} (x, θ) = \sum_{m = 1}^{\infty} \sum_{j = 1}^{4} \frac{1}{R} (β_{j} - k_{θ j}) (a_{j} e^{k_{θ j} θ} - d_{j} e^{- k_{θ j} θ}) \sin (k_{x} x) .

Meanwhile, substitution of Eqs. (59)-(61) into the Fourier transforms of Eqs. (40), (44), (50) and (52) yields the frequency domain expressions of the force and moment resultants in the OCCS:

67

{\tilde{N}}_{θ} = \sum_{m = 1}^{\infty} \sum_{j = 1}^{4} \frac{C}{R} (λ_{1} + λ k_{θ j}^{2} - μ R k_{x} α_{j} + k_{θ j} β_{j}) (a_{j} e^{k_{θ j} θ} + d_{j} e^{- k_{θ j} θ}) \sin (k_{x} x),

68

{\tilde{M}}_{θ} = \sum_{m = 1}^{\infty} \sum_{j = 1}^{4} - \frac{D}{R^{2}} (1 + k_{θ j}^{2} - μ R^{2} k_{x}^{2}) (a_{j} e^{k_{θ j} θ} + d_{j} e^{- k_{θ j} θ}) \sin (k_{x} x),

69

{\tilde{F}}_{θ x} = \sum_{m = 1}^{\infty} \sum_{j = 1}^{4} \frac{μ_{2} C}{R} (λ R k_{x} k_{θ j} + λ_{1} k_{θ j} α_{j} + R k_{x} β_{j}) (a_{j} e^{k_{θ j} θ} - d_{j} e^{- k_{θ j} θ}) \cos (k_{x} x),

70

{\tilde{V}}_{θ z} = \sum_{m = 1}^{\infty} \sum_{j = 1}^{4} \frac{D}{R^{3}} [\begin{matrix} (2 - μ) R^{2} k_{x}^{2} k_{θ j} - k_{θ j}^{3} - k_{θ j} \\ + μ_{2} R k_{x} k_{θ j} α_{j} - 3 μ_{2} R^{2} k_{x}^{2} β_{j} \end{matrix}] (a_{j} e^{k_{θ j} θ} - d_{j} e^{- k_{θ j} θ}) \sin (k_{x} x) .

For an arbitrary axial mode number $m$ , Eqs. (59)-(61) and (66) can be expressed in matrix form as:

71

W_{d} = H_{m} (x) W_{d}^{*},

where $W_{d}$ denotes the displacement vector of the OCCS, $H_{m} (x)$ indicates the axial mode matrix and $W_{d}$ ^* represents the vector of the circumferential traveling wave solutions corresponding to the displacement vector. They are presented in detail as follows:

72

W_{d} = {\{\tilde{u} \tilde{v} \tilde{w} {\tilde{φ}}_{θ}\}}^{T},

73

H_{m} (x) = d i a g \{\cos (k_{x} x) \sin (k_{x} x) \sin (k_{x} x) \sin (k_{x} x)\},

74

W_{d}^{*} = A_{d} P_{h} (- θ) a + D_{d} P_{h} (θ) d,

in which $P_{h} (θ)$ denotes the phase matrix. $a$ and $d$ are amplitude vectors corresponding to the arriving wave and the departing wave of the displacements of the OCCS, respectively. They are presented in detail as follows:

75

P_{h} (θ) = d i a g \{e^{- k_{θ 1} θ} e^{- k_{θ 2} θ} e^{- k_{θ 3} θ} e^{- k_{θ 4} θ}\},

76

a = {\{a_{1} a_{2} a_{3} a_{4}\}}^{T},

77

d = {\{d_{1} d_{2} d_{3} d_{4}\}}^{T},

and $A_{d}$ and $D_{d}$ are coefficient matrices corresponding to the arriving wave and the departing wave of the displacements of the OCCS, respectively. The elements of the coefficient matrices $A_{d}$ and $D_{d}$ are listed as follows:

78

A_{d} (1, j) = D_{d} (1, j) = α_{j},

79

A_{d} (2, j) = {- D}_{d} (2, j) = β_{j},

80

A_{d} (3, j) = D_{d} (3, j) = 1,

81

A_{d} (4, j) = {- D}_{d} (4, j) = \frac{(β_{j} - k_{θ j})}{R},

where $j =$ 1, 2, 3, 4.

Similarly, for an arbitrary axial mode number $m$ , Eqs. (67)-(70) can be expressed in matrix form as:

82

W_{f} = H_{m} (x) W_{f}^{*},

where the physical significance and expression of $H_{m} (x)$ are the same as those presented in Eq. (71). $W_{f}$ denotes the force vector of the shell, and $W_{f}^{*}$ represents the vector of the circumferential wave solutions corresponding to the force vector. They are presented in detail as follows:

83

W_{f} = {\{{\tilde{F}}_{θ x} {\tilde{N}}_{θ} {\tilde{V}}_{θ z} {\tilde{M}}_{θ}\}}^{T},

84

W_{f}^{*} = A_{f} P_{h} (- θ) a + D_{f} P_{h} (θ) d,

in which $A_{f}$ and $D_{f}$ are coefficient matrices corresponding to the arriving wave and the departing wave of the force and moment resultants of the OCCS, respectively. The elements of the coefficient matrices $A_{f}$ and $D_{f}$ are listed as follows:

85

A_{f} (1, j) = {- D}_{f} (1, j) = \frac{(λ R k_{x} k_{θ j} + λ_{1} k_{θ j} α_{j} + R k_{x} β_{j}) μ_{2} C}{R},

86

A_{f} (2, j) = D_{f} (2, j) = \frac{(λ_{1} + λ k_{θ j}^{2} - μ R k_{x} α_{j} + k_{θ j} β_{j}) C}{R},

87

A_{f} (3, j) = - D_{f} (3, j) = \frac{[(2 - μ) R^{2} k_{x}^{2} k_{θ j} - k_{θ j}^{3} - k_{θ j} + μ_{2} R k_{x} k_{θ j} α_{j} - 3 μ_{2} R^{2} k_{x}^{2} β_{j}] D}{R^{3}},

88

A_{f} (4, j) = D_{f} (4, j) = - \frac{(1 + k_{θ j}^{2} - μ R^{2} k_{x}^{2}) D}{R^{2}},

where $j =$ 1, 2, 3, 4.

2.5. Equation of natural frequencies for the plate/shell coupled structures

Taking advantage of the unidirectional wave form solutions of matrix form for the thin plate obtained in Subsection 2.2 and for the OCCS obtained in Subsection 2.4, the MRRM is introduced to derive the equation of the natural frequencies of the plate/shell coupled structures.

Firstly, the plate/shell coupled structure is discretized into basic components such as flat plates and OCCSs. A dual local coordinate system is established for each of the components at both of the ends, where the cartesian coordinate for a flat plate and the circular cylindrical coordinate for an OCCS. Then, the local scattering matrix is derived according to the continuity conditions of the displacements and the equilibrium conditions of the internal forces and moments at each of the joints of the plate/shell coupled structure. Meanwhile, the local phase matrix is obtained according to the inherent relations of the harmonic waves in the dual local coordinate system. With all of the local scattering matrices and all of the local phase matrices respectively assembled into a global scattering matrix and a global phase matrix, the global scattering equation and the global phase equation are obtained. When keeping the two global amplitude vectors of the arriving wave the same, the two global amplitude vectors of the departing wave contain the same scalar state variables arranged in different sequential orders. Therefore, a permutation equation can be obtained from the relation between the two global amplitude vectors of the departing wave. Subsequently, the reverberation-ray matrix can be obtained from the simultaneous equations of the global scattering equation, the global phase equation and the permutation equation. Finally, the equation of the natural frequencies can be derived by equating the determinant of the coefficient matrix of the global amplitude vector of the departing wave to zero.

With the derivation procedure mentioned above, the equations of the natural frequencies of the three plate/shell coupled structures including a box-type structure, a racetrack cylindrical shell and a ship hull structure will be obtained in the following discussions in this subsection. However, since the three independent derivation procedures are quite similar to each other, for simplicity, one of them will be taken as an example and the other two will be omitted. Note that the solutions obtained in Subsection 2.2 are applied for flat plate components while the solutions obtained in Subsection 2.4 are applied for OCCS components.

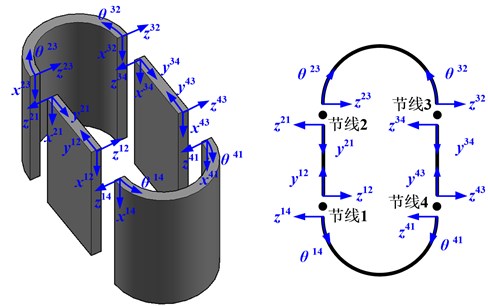
Next, the derivation for equation of the natural frequencies of the racetrack cylindrical shell shown in Fig. 3, is presented as follows.

Fig. 3Dual local coordinate systems for the racetrack cylindrical shell

2.5.1. Scattering matrix

The continuity conditions for the plate and the OCCS at Node Line 1 are presented as follows:

89

u^{12} = u^{14}, v^{12} + v^{14} = 0, w^{12} + w^{14} = 0, φ_{y}^{12} = φ_{θ}^{14},

which can be rewritten in matrix form as:

90

W_{d}^{12} = T_{d}^{1} W_{d}^{14},

where $T_{d}^{1} = d i a g \{1 - 1 - 11\}$ denotes the transfer matrix corresponding to the displacement vector at Node Line 1. The variables with superscript $I J$ ( $I$ , $J =$ 1-4) indicate the physical quantities of the substructure bounded by Node Line $I$ and Node Line $J$ , this will not be mentioned repeatedly in the following discussions.

Since the local coordinates are established at the node lines, the phase matrix turns to be a unit matrix at the node lines. Taking into account of this condition and substituting Eqs. (26) and (71) into Eq. (90) yields:

91

A_{d}^{12} a^{12} + D_{d}^{12} d^{12} = T_{d}^{1} (A_{d}^{14} a^{14} + D_{d}^{14} d^{14}) .

Meanwhile, the equilibrium conditions for the plate and the OCCS at Node Line 1 are presented as:

92

N_{y x}^{12} + F_{θ x}^{14} = 0, N_{y}^{12} = N_{θ}^{14}, V_{y z}^{12} = V_{θ z}^{14}, M_{y}^{12} + M_{θ}^{14} = 0,

which can be rewritten in matrix form as:

93

W_{f}^{12} = T_{f}^{1} W_{f}^{14},

where $T_{f}^{1} = - T_{d}^{1}$ denotes the transfer matrix corresponding to the force vector at Node Line 1.

Substitution of Eqs. (34) and (82) into Eq. (93) results in:

94

A_{f}^{12} a^{12} + D_{f}^{12} d^{12} = T_{f}^{1} (A_{f}^{14} a^{14} + D_{f}^{14} d^{14}) .

Eqs. (91) and (94) can be combined and expressed in a single matrix form as:

95

d^{1} = S^{1} a^{1},

where $d^{1} = {\{{(d^{14})}^{T} {(d^{12})}^{T}\}}^{T}$ and $a^{1} = {\{{(a^{14})}^{T} {(a^{12})}^{T}\}}^{T}$ are amplitude coefficients of the departing wave and arriving wave at Node Line 1, respectively. $S^{1}$ , the scattering matrix at Node Line 1, is defined as:

96

S^{1} = - {[\begin{matrix} T_{d}^{1} D_{d}^{14} & - D_{d}^{12} \\ T_{f}^{1} D_{f}^{14} & - D_{f}^{12} \end{matrix}]}^{- 1} [\begin{matrix} T_{d}^{1} A_{d}^{14} & - A_{d}^{12} \\ T_{f}^{1} A_{f}^{14} & - A_{f}^{12} \end{matrix}] .

In the same manner, the scattering relations and scattering matrices for the rest node lines can be obtained. For simplicity, the derivation procedures are omitted and the results are given straightforwardly as follows.

The scattering relations at an arbitrary node line $J$ can be presented as:

97

d^{J} = S^{J} a^{J},

where $d^{J} = {\{{(d^{J I})}^{T} {(d^{J K})}^{T}\}}^{T}$ and $a^{J} = {\{{(a^{J I})}^{T} {(a^{J K})}^{T}\}}^{T}$ are amplitude coefficients of the departing wave and arriving wave at Node Line $J$ , respectively. $S^{J}$ , the scattering matrix at Node Line $J$ , is defined as:

98

S^{J} = - {[\begin{matrix} T_{d}^{J} D_{d}^{J I} & - D_{d}^{J K} \\ T_{f}^{J} D_{f}^{J I} & - D_{f}^{J K} \end{matrix}]}^{- 1} [\begin{matrix} T_{d}^{J} A_{d}^{J I} & - A_{d}^{J K} \\ T_{f}^{J} A_{f}^{J I} & - A_{f}^{J K} \end{matrix}],

in which $J =$ 2, 3, 4. As $J =$ 2 and 3, $I = J - 1$ and $K = J + 1$ . However, as $J =$ 4, $I =$ 3 and $K =$ 1.

Assembling all of the local scattering equations for Node Line 1-4 by stacking $d^{1}$ - $d^{4}$ and $a^{1}$ - $a^{4}$ into two column vectors $d$ and $a$ , the global scattering equation can be obtained as follows:

99

d = S a,

where $d$ and $a$ are global amplitude vectors of the departing wave and the arriving wave, and $S$ is the global scattering matrix. They are presented in detail as follows:

100

d = {\{d^{1} d^{2} d^{3} d^{4}\}}^{T} = {\{d^{14} d^{12} d^{21} d^{23} d^{32} d^{34} d^{43} d^{41}\}}^{T},

101

a = {\{a^{1} a^{2} a^{3} a^{4}\}}^{T} = {\{a^{14} a^{12} a^{21} a^{23} a^{32} a^{34} a^{43} a^{41}\}}^{T},

102

S = d i a g \{S^{1} S^{2} S^{3} S^{4}\} .

2.5.2. Phase matrix

The phase relations of harmonic waves in the dual coordinate system provide additional equations for solving the unknown amplitude vectors. Note that the departing wave from Node Line 1 (3) is exactly the arriving wave to Node Line 2 (4), and vice versa. Therefore, the amplitudes of the departing wave and the arriving wave differ with each other by a phase factor.

With the employment of the solutions for the plate obtained in Subsection 2.2, the relations between the amplitudes of the departing wave and the arriving wave between Node Line 1 (3) and Node Line 2 (4) are presented as:

103

a_{1}^{I J} = - e^{- k_{y 1} L_{y}} d_{1}^{J I}, a_{2}^{I J} = - e^{- k_{y 2} L_{y}} d_{2}^{J I}, a_{3}^{I J} = - e^{- k_{y 3} L_{y}} d_{3}^{J I}, a_{4}^{I J} = - e^{- k_{y 4} L_{y}} d_{4}^{J I},

104

a_{1}^{J I} = - e^{- k_{y 1} L_{y}} d_{1}^{I J}, a_{2}^{J I} = - e^{- k_{y 2} L_{y}} d_{2}^{I J}, a_{3}^{J I} = - e^{- k_{y 3} L_{y}} d_{3}^{I J}, a_{4}^{J I} = - e^{- k_{y 4} L_{y}} d_{4}^{I J},

where $I J =$ 12 or 34 and $J I =$ 21 or 43.

Similarly, with the employment of the solutions for the OCCS obtained in Subsection 2.4, the relations between the amplitudes of the departing wave and the arriving wave between Node Line 2 (4) and Node Line 3 (1) are presented as:

105

a_{1}^{I J} = - e^{- k_{θ 1} θ_{0}} d_{1}^{J I}, a_{2}^{I J} = - e^{- k_{θ 2} θ_{0}} d_{2}^{J I}, a_{3}^{I J} = - e^{- k_{θ 3} θ_{0}} d_{3}^{J I}, a_{4}^{I J} = - e^{- k_{θ 4} θ_{0}} d_{4}^{J I},

106

a_{1}^{J I} = - e^{- k_{θ 1} θ_{0}} d_{1}^{I J}, a_{2}^{J I} = - e^{- k_{θ 2} θ_{0}} d_{2}^{I J}, a_{3}^{J I} = - e^{- k_{θ 3} θ_{0}} d_{3}^{I J}, a_{4}^{J I} = - e^{- k_{θ 4} θ_{0}} d_{4}^{I J},

where $I J =$ 23 or 41 and $J I =$ 32 or 14.

Assembling all of the local phase equations defined by Eqs. (103)-(106) results in the global phase equation:

107

a = P d^{*},

where the physical significance and expression of $a$ are the same as the one presented in Eq. (99). $d^{*}$ is a rearranged global amplitude vector of the departing wave, and $P$ is the global phase matrix. They are presented in detail as follows:

108

d^{*} = {\{d^{41} d^{21} d^{12} d^{32} d^{23} d^{43} d^{34} d^{14}\}}^{T},

109

P = - d i a g \{P_{h} (θ_{0}) P_{h} (L_{y}) P_{h} (L_{y}) P_{h} (θ_{0}) P_{h} (θ_{0}) P_{h} (L_{y}) P_{h} (L_{y}) P_{h} (θ_{0})\},

where $θ_{0}$ denotes the included angle of the OCCS, and $L_{y}$ represents the length of the plate in y direction.

2.5.3. Permutation matrix

A comparison of the global amplitude vectors of the departing wave $d$ and $d^{*}$ indicates that the two amplitude vectors contain the same scalar state variables arranged in different sequential orders. The relation between $d$ and $d^{*}$ is:

110

d^{*} = U d,

where $U$ is the permutation matrix, which is presented in detail as follows:

111

U = [\begin{matrix} \begin{matrix} \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ I_{4} & 0_{4} \end{matrix} \\ \begin{matrix} 0_{4} & I_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} \end{matrix} & \begin{matrix} \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & I_{4} \\ 0_{4} & 0_{4} \end{matrix} \\ \begin{matrix} 0_{4} & 0_{4} \\ I_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} \end{matrix} \\ \begin{matrix} \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & I_{4} \\ 0_{4} & 0_{4} \end{matrix} \\ \begin{matrix} 0_{4} & 0_{4} \\ I_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} \end{matrix} & \begin{matrix} \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ I_{4} & 0_{4} \end{matrix} \\ \begin{matrix} 0_{4} & I_{4} \\ 0_{4} & 0_{4} \end{matrix} & \begin{matrix} 0_{4} & 0_{4} \\ 0_{4} & 0_{4} \end{matrix} \end{matrix} \end{matrix}],

in which $0_{4}$ and $I_{4}$ are respectively zero matrix and unit matrix of fourth order.

2.5.4. Reverberation-ray matrix and the equation of natural frequencies

Substitution of Eqs. (107) and (110) into Eq. (99) yields:

112

(I - R) d = 0,

where $I$ is a unit matrix of 32nd order, and $R = S P U$ is defined as the reverberation-ray matrix of the racetrack cylindrical shell.

To obtain a nontrivial solution of the global amplitude vector of the departing wave, the determinant of $(I - R)$ must be zero, namely:

113

d e t (I - R) = 0,

which is the equation of natural frequencies of the racetrack cylindrical shell.

2.6. Searching algorithm for natural frequencies

As the equation of natural frequencies of the plate/shell coupled structure is obtained, the problem at hand is to solve the equation for the natural frequencies. It is obvious that the left hand side of Eq. (113) is a function of frequency, and the natural frequencies are zeros of the function. Unfortunately, for most of the frequencies, the function values are complex numbers. Therefore, finding the zeros of the function needs to search the common zeros of the real part and the imaginary part of the function. A good idea is to search the zeros or the minimal values of the absolute value of the function. This simple approach is adopted in this paper and the golden section search algorithm is introduced to determine the natural frequencies of the plate/shell coupled structure. The procedure for determining the natural frequencies of the plate/shell coupled structure is same to the one for free vibration analysis of open and closed circular cylindrical shell by MRRM presented in [52-54].

3. Results and discussions

In this section, free vibration analysis of plate/shell coupled structures with two opposite edges simply supported is presented to verify the validity and accuracy of the present method. The natural frequencies of the three plate/shell coupled structures are calculated by MRRM and by FEM, and the comparison results are presented in tabular form. It is particularly pointed out that all the results obtained by FEM in the following discussions are calculated with the commercial software ANSYS.

3.1. The box-type structure

Studies on the free vibration of the box-type structure, as shown in Fig. 4, with two opposite edges simply supported are conducted in this subsection. The material properties of the box-type structure are: Young’s modulus $E =$ 2.1×10¹¹ Pa, Poisson’s ratio $μ =$ 0.3, mass density $ρ =$ 7800 kg m⁻³, and the geometrical parameters of the box-type structure are: $L_{x} =$ 10 m, $L_{y 1} = L_{y 2} =$ 4 m, $h =$ 0.01 m. The results for natural frequencies of the box-type structure obtained by MRRM are compared with those obtained by FEM in Table 1, where $m$ denotes the axial mode number, $n$ represents the mode number in the circumferential direction, and P-Error indicates the percentage error between the results obtained by MRRM and FEM.

Fig. 4Geometry and notations of a box-type structure

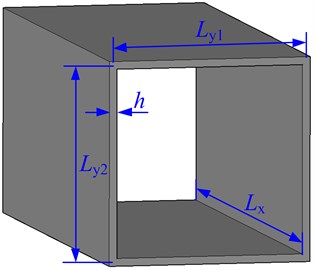
Table 1Comparison of natural frequencies obtained by MRRM and FEM for the box-type structure

Mode number		Natural frequencies and percentage errors
$n$	$m$	1	2	3	4	5	6	7	8
1	FEM	1.787	2.526	3.758	5.484	7.703	10.416	13.621	17.320
	MRRM	1.788087	2.528058	3.761279	5.487782	7.707571	10.420647	13.627011	17.326663
	P-Error	0.06 %	0.08 %	0.09 %	0.07 %	0.06 %	0.04 %	0.04 %	0.04 %
2	FEM	2.596	3.206	4.305	5.926	8.067	10.723	13.886	17.552
	MRRM	2.597011	3.207152	4.307759	5.928857	8.070860	10.726757	13.890259	17.556971
	P-Error	0.04 %	0.04 %	0.06 %	0.05 %	0.05 %	0.04 %	0.03 %	0.03 %
3	FEM	3.635	4.116	5.053	6.523	8.548	11.117	14.217	17.835
	MRRM	3.633189	4.116464	5.053479	6.524894	8.550082	11.119675	14.219630	17.838747
	P-Error	0.05 %	0.01 %	0.01 %	0.03 %	0.02 %	0.02 %	0.02 %	0.02 %
4	FEM	6.411	7.149	8.380	10.104	12.321	15.032	18.236	21.934
	MRRM	6.412601	7.152497	8.385686	10.112165	12.331930	15.044982	18.251319	21.950942
	P-Error	0.02 %	0.05 %	0.07 %	0.08 %	0.09 %	0.09 %	0.08 %	0.08 %
5	FEM	8.015	8.662	9.768	11.357	13.445	16.039	19.142	22.752
	MRRM	8.012426	8.664084	9.772218	11.363087	13.452738	16.048779	19.153304	22.765631
	P-Error	0.03 %	0.02 %	0.04 %	0.05 %	0.06 %	0.06 %	0.06 %	0.06 %
6	FEM	9.798	10.384	11.374	12.824	14.768	17.224	20.203	23.706
	MRRM	9.817337	10.387455	11.377389	12.827979	14.772323	17.230424	20.210830	23.714801
	P-Error	0.20 %	0.03 %	0.03 %	0.03 %	0.03 %	0.04 %	0.04 %	0.04 %
7	FEM	14.118	14.855	16.085	17.807	20.023	22.732	25.934	29.629
	MRRM	14.115270	14.858683	16.092494	17.819161	20.038987	22.752050	25.958374	29.657972
	P-Error	0.02 %	0.02 %	0.05 %	0.07 %	0.08 %	0.09 %	0.09 %	0.10 %
8	FEM	16.484	17.169	18.300	19.901	21.984	24.560	27.633	31.209
	MRRM	16.503369	17.175778	18.307301	19.910498	21.997010	24.575867	27.653055	31.231947
	P-Error	0.12 %	0.04 %	0.04 %	0.05 %	0.06 %	0.06 %	0.07 %	0.07 %

It can be found from Table 1 that, the natural frequencies obtained by MRRM and FEM agree well with each other. The maximum of the percentage errors is 0.20 %, and most of the percentage errors are no larger than 0.10 %. The small discrepancies in the results should be attributed to the approximation of FEM. Therefore, it indicates that MRRM is validate and of high precision for free vibration analysis of plate coupled structures such as the box-type structure.

3.2. The racetrack cylindrical shell

Consider an isotropic, racetrack cylindrical shell composed of thin plates and OCCSs with axial length $L_{x} =$ 10 m, uniform thickness $h =$ 0.01 m, circumferential length of the plate $L_{y} =$ 4 m, middle surface radius of the OCCS $R =$ 2 m, as shown in Fig. 5. The material properties of the racetrack cylindrical shell are the same as those defined for the box-type structure. The results for the natural frequencies of the racetrack cylindrical shell obtained by MRRM are compared with those obtained by FEM in Table 2, in which the notations are of the same meaning as those in Table 1.

Table 2 shows that the natural frequencies obtained by MRRM and FEM agree well with each other. The maximum of the percentage errors is 1.34%, and most of the percentage errors are no larger than 1.00 %. The difference between the results obtained by MRRM and FEM may be caused by the approximation of FEM and the different shell theories adopted by FEM and this paper. Therefore, it indicates that MRRM is validate for free vibration analysis of plate-shell coupled structures such as the racetrack cylindrical shell, and the results are of high precision.

Table 2Comparison of natural frequencies obtained by MRRM and FEM for the racetrack cylindrical shell

Mode number		Natural frequencies and percentage errors
$n$	$m$	1	2	3	4	5	6	7	8
1	FEM	2.151	2.953	4.090	5.715	7.854	10.508	13.670	17.336
	MRRM	2.151035	2.957795	4.099758	5.727604	7.869848	10.525766	13.689947	17.357884
	P-Error	0.00 %	0.16 %	0.24 %	0.22 %	0.20 %	0.17 %	0.15 %	0.13 %
2	FEM	5.383	6.984	8.461	10.232	12.415	15.064	18.200	21.832
	MRRM	5.456198	7.031901	8.506268	10.281368	12.471784	15.128039	18.271764	21.911835
	P-Error	1.34 %	0.68 %	0.53 %	0.48 %	0.46 %	0.42 %	0.39 %	0.36 %
3	FEM	5.444	13.162	15.027	17.038	19.382	22.133	25.328	28.989
	MRRM	5.514263	13.195591	15.093706	17.133938	19.500229	22.270141	25.483314	29.162474
	P-Error	1.27 %	0.25 %	0.44 %	0.56 %	0.61 %	0.62 %	0.61 %	0.59 %
4	FEM	10.458	20.291	23.281	25.846	28.524	31.492	34.835	38.598
	MRRM	10.460565	20.468996	23.452468	26.038717	28.741440	31.738403	35.110916	38.903664
	P-Error	0.02 %	0.87 %	0.73 %	0.74 %	0.76 %	0.78 %	0.79 %	0.79 %
5	FEM	10.684	20.334	33.382	36.659	39.751	43.017	46.583	50.513
	MRRM	10.687016	20.525417	33.560942	36.926488	40.084378	43.403142	47.016813	50.994129
	P-Error	0.03 %	0.93 %	0.53 %	0.72 %	0.83 %	0.89 %	0.92 %	0.94 %
6	FEM	13.803	27.932	33.447	48.481	52.618	56.447	60.381	64.577
	MRRM	13.927559	27.962842	33.633721	48.880722	53.107713	57.012575	61.015628	65.278488
	P-Error	0.89 %	0.11 %	0.56 %	0.82 %	0.92 %	0.99 %	1.04 %	1.07 %
7	FEM	15.378	28.755	42.048	48.529	66.309	71.352	75.927	80.554
	MRRM	15.492372	28.837613	42.200925	48.948598	66.815182	72.081826	76.777865	81.507231
	P-Error	0.74 %	0.29 %	0.36 %	0.86 %	0.76 %	1.01 %	1.11 %	1.17 %
8	FEM	15.955	30.057	42.961	57.665	72.451	84.556	92.219	97.881
	MRRM	15.956436	30.175983	43.324195	57.735824	72.588720	84.589523	93.167426	99.063747
	P-Error	0.01 %	0.39 %	0.84 %	0.12 %	0.19 %	0.04 %	1.02 %	1.19 %

Fig. 5Geometry and notations of a racetrack cylindrical shell

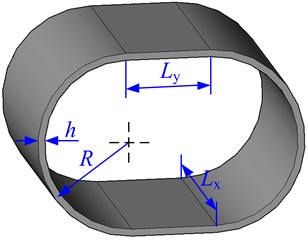
Fig. 6Geometry and notations of a ship hull structure

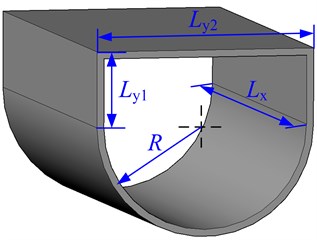
3.3. The ship hull structure

In this subsection, the natural frequencies of the ship hull structure, as shown in Fig. 6, with two opposite edges simply supported are calculated. The material properties of the ship hull structure are the same as those defined for the box-type structure. The geometrical parameters are: $L_{x} =$ 10 m, $L_{y 1} =$ 2 m, $L_{y 2} =$ 4m, $R =$ 2 m and $h =$ 0.01 m. The results for the natural frequencies of the box-type structure obtained by MRRM are compared with those obtained by FEM in Table 3, where the notations are of the same meaning as those in Tables 1 and 2.

Table 3Comparison of natural frequencies obtained by MRRM and FEM for the ship hull structure

Mode number		Natural frequencies and percentage errors
$n$	$m$	1	2	3	4	5	6	7	8
1	FEM	2.562	5.713	6.575	8.847	13.875	16.349	16.377	20.440
	MRRM	2.574674	5.803015	6.651149	8.818441	13.925635	16.342406	17.035003	20.525130
	P-Error	0.49 %	1.55 %	1.14 %	0.32 %	0.36 %	0.04 %	3.86 %	0.41 %
2	FEM	3.217	7.027	8.241	9.973	16.702	21.496	22.775	28.663
	MRRM	3.222129	7.072771	8.300801	9.991594	16.703286	21.734920	23.026966	27.617563
	P-Error	0.16 %	0.65 %	0.72 %	0.19 %	0.01 %	1.10 %	1.09 %	3.79 %
3	FEM	4.318	8.407	9.681	11.209	18.061	24.346	25.892	30.900
	MRRM	4.322056	8.441562	9.737088	11.237360	18.073568	24.512647	26.124280	31.037877
	P-Error	0.09 %	0.41 %	0.58 %	0.25 %	0.07 %	0.68 %	0.89 %	0.44 %
4	FEM	5.934	10.159	11.372	12.757	19.754	26.778	28.435	32.886
	MRRM	5.937682	10.193966	11.432079	12.791735	19.773413	26.937417	28.661965	33.011183
	P-Error	0.06 %	0.34 %	0.53 %	0.27 %	0.10 %	0.59 %	0.79 %	0.38 %
5	FEM	8.071	12.362	13.460	14.723	21.882	29.349	31.044	35.145
	MRRM	8.075624	12.400127	13.527708	14.764371	21.906555	29.520271	31.286598	35.270387
	P-Error	0.06 %	0.31 %	0.50 %	0.28 %	0.11 %	0.58 %	0.78 %	0.36 %
6	FEM	10.725	15.043	16.010	17.168	24.480	32.245	33.918	37.775
	MRRM	10.729149	15.085841	16.086390	17.215377	24.509296	32.435677	34.185502	37.908113
	P-Error	0.04 %	0.28 %	0.47 %	0.28 %	0.12 %	0.59 %	0.78 %	0.35 %
7	FEM	13.886	18.212	19.052	20.122	27.566	35.541	37.152	40.826
	MRRM	13.891362	18.261305	19.137747	20.174461	27.599471	35.755749	37.449705	40.969879
	P-Error	0.04 %	0.27 %	0.45 %	0.26 %	0.12 %	0.60 %	0.79 %	0.35 %
8	FEM	17.552	21.874	22.599	23.598	31.149	39.276	40.800	44.330
	MRRM	17.557387	21.930540	22.694437	23.653557	31.186065	39.516188	41.130030	44.484581
	P-Error	0.03 %	0.26 %	0.42 %	0.23 %	0.12 %	0.61 %	0.80 %	0.35 %

It can be observed from Table 3 that, the natural frequencies obtained by MRRM and FEM agree well with each other. Except for certain mode numbers, the maximum of the percentage errors is 1.55 %, and most of the percentage errors are no larger than 1.00 %. The difference between the results obtained by MRRM and FEM may be caused by the approximation of FEM and the different shell theories adopted by FEM and this paper. Therefore, it indicates that MRRM is applicable for free vibration analysis of plate-shell coupled structures such as the ship hull structure, and the results are of high precision.

4. Conclusions

This paper presents a semi-analytical solution procedure and accurate calculation results for plate/shell coupled structures with two opposite edges simply supported. The validity and applicability of the MRRM for free vibration analysis of plate/shell coupled structures are verified. It has been proved that the results obtained by MRRM are in excellent agreement with those obtained by FEM and that high precision of MRRM has been shown. MRRM is advantageous in its simple and uniform formulation as well as accurate results for dynamic response analysis of coupled structures.

It should be pointed out that the method of reverberation-ray matrix only applies to plate/shell coupled structures with two opposite edges simply-supported at present. This limitation may be breached by replacing the standing wave form solution with the combination of the trigonometric function and the tangent or cotangent functions. The effects of the structural parameters, boundary conditions and connection forms on the vibration characteristics of the plate/shell coupled structures will be discussed in the subsequent researches.

References

Irie T., Yamada G., Kobayash Y. Free vibration of a cantilever folded plate. The Journal of the Acoustical Society of America, Vol. 76, Issue 6, 1984, p. 1743-1748.

Publisher
Eterovic A. L., Godoy L. A. An exact strip method for folded plate structures. Computers and Structures, Vol. 32, Issue 2, 1989, p. 263-276.

Publisher
Maleki S. Compound strip method for box girders and folded plates. Computers and Structures, Vol. 40, Issue 3, 1991, p. 527-538.

Publisher
Liu W. H., Huang C. C. Vibration analysis of folded plates. Journal of Sound and Vibration, Vol. 157, Issue 1, 1992, p. 123-137.

Publisher
Hinton E., Özakça M., Rao N. V. R. Free vibration analysis and shape optimization of variable thickness plates, prismatic folded plates and curved shells. Part 1: finite strip formulation. Journal of Sound and Vibration, Vol. 181, Issue 4, 1995, p. 553-566.

Publisher
Niyogi A. G., Laha M. K., Sinha P. K. Finite element vibration analysis of laminated composite folded plate structures. Shock and Vibration, Vol. 6, Issues 5-6, 1999, p. 273-283.

Publisher
Samanta A., Mukhopadhyay M. Finite element static and dynamic analyses of folded plates. Engineering Structures, Vol. 21, Issue 3, 1999, p. 277-287.

Publisher
Lai Y., Yu W. Analytical solution for forced vibration of a simply-supported V-shaped folded plate roof. Thin-Walled Structures, Vol. 40, Issue 3, 2002, p. 215-223.

Publisher
Peng L. X., Kitipornchai S., Liew K. M. Free Vibration Analysis of Folded Plate Structures by the FSDT Mesh-free Method. Computational Mechanics, Vol. 39, Issue 6, 2007, p. 799-814.

Publisher
Cuschieri J. M. Structural power-flow analysis using a mobility approach of an L-shaped plate. The Journal of the Acoustical Society of America, Vol. 87, Issue 3, 1990, p. 1159-1165.

Publisher
Cuschieri J. M. Parametric analysis of the power flow on an L-shaped plate using a mobility power flow approach. The Journal of the Acoustical Society of America, Vol. 91, Issue 5, 1992, p. 2686-2695.

Publisher
Wang Z. H., Xing J. T., Price W. G. An investigation of power flow characteristics of L-shaped plates adopting a substructure approach. Journal of Sound and Vibration, Vol. 250, Issue 4, 2002, p. 627-648.

Publisher
Kessissoglou N. J. Power transmission in L-shaped plates including flexural and in-plane vibration. The Journal of the Acoustical Society of America, Vol. 115, Issue 3, 2004, p. 1157-1169.

Publisher
Chen X., Sheng M. Research on vibration characteristics of L-shaped plate using a mobility power flow approach. Journal of Marine Science and Application, Vol. 6, Issue 3, 2007, p. 12-16.

Publisher
Liu C., Li F., Huang W. Active vibration control of finite L-shaped beam with travelling wave approach. Acta Mechanica Solida Sinica, Vol. 23, Issue 5, 2010, p. 377-385.

Publisher
Lin T. R., Tan C. C., Yan C., Hargreaves D. Vibration of L-shaped plates under a deterministic force or moment excitation: a case of statistical energy analysis application. Journal of Sound and Vibration, Vol. 330, Issue 20, 2011, p. 4780-4797.

Publisher
Liu C., Li F., Tang L., Huang W. Vibration control of the finite L-shaped beam structures based on the active and reactive power flow. Science China Physics, Mechanics and Astronomy, Vol. 54, Issue 2, 2011, p. 310-319.

Publisher
Liu C., Li F., Liang T., Huang W. Early short time transient response of finite L-shaped Mindlin plate. Wave Motion, Vol. 48, Issue 5, 2011, p. 371-391.

Publisher
Liu C., Li F., Liang T., Huang W. The wave and vibratory power transmission in a finite L-shaped Mindlin plate with two simply supported opposite edges. Acta Mechanica Sinica, Vol. 27, Issue 5, 2011, p. 785-795.

Publisher
Lin Y., Wu W., Li X., Gan J. Study on transmission law of flexural waves through L-shaped steel-aluminum joints. The Twenty-second International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers, 2012.

Search CrossRef
Dickinson S., Warburton G. Vibration of box-type structures. Journal of Mechanical Engineering Science, Vol. 9, Issue 4, 1967, p. 325-338.

Publisher
Popplewell N. The vibration of a box-type structure I. Natural frequencies and normal modes. Journal of Sound and Vibration, Vol. 14, Issue 3, 1971, p. 357-365.

Publisher
Handa K. Analysis of in-plane vibration of box-type structures by a finite element method. Journal of Sound and Vibration, Vol. 21, Issue 1, 1972, p. 107-114.

Publisher
Fulford R. A., Petersson B. A. T. Estimation of vibrational power in built-up systems involving box-like structures. Part 1: uniform force distribution. Journal of Sound and Vibration, Vol. 232, Issue 5, 2000, p. 877-895.

Publisher
Fulford R. A., Petersson B. A. T. Estimation of vibrational power in built-up systems involving box-like structures. Part 2: infinite top-plate and circular geometry. Journal of Sound and Vibration, Vol. 232, Issue 5, 2000, p. 897-915.

Publisher
Lee S. Y., Wooh S. C. Finite element vibration analysis of composite box structures using the high order plate theory. Journal of Sound and Vibration, Vol. 277, Issues 4-5, 2004, p. 801-814.

Publisher
Lin T. R., Pan J. Vibration characteristics of a box-type structure. Journal of Vibration and Acoustics, Vol. 131, Issue 3, 2009, p. 1-9.

Publisher
Lin T. R., Pan J. Sound radiation characteristics of a box-type structure. Journal of Sound and Vibration, Vol. 325, Issues 4-5, 2009, p. 835-851.

Publisher
Chen Y., Jin G., Zhu M., Liu Z., Du J., Li W. Vibration behaviors of a box-type structure built up by plates and energy transmission through the structure. Journal of Sound and Vibration, Vol. 331, Issue 4, 2012, p. 849-867.

Publisher
Yamada G., Irie T., Tamiya T. Free vibration of a circular cylindrical double-shell system closed by end plates. Journal of Sound and Vibration, Vol. 108, Issue 2, 1986, p. 297-304.

Publisher
Schlesinger A. Transmission of elastic waves from a cylinder to an attached flat plate. Journal of Sound and Vibration, Vol. 186, Issue 5, 1995, p. 761-780.

Publisher
Tso Y. K., Hansen C. H. Wave propagation through cylinder/plate junctions. Journal of Sound and Vibration, Vol. 186, Issue 3, 1995, p. 447-461.

Publisher
Stanley A. J., Ganesan N. Frequency response of shell-plate combinations. Computers and Structures, Vol. 59, Issue 6, 1996, p. 1083-1094.

Publisher
Tso Y. K., Hansen C. H. An investigation of the coupling loss factor for a cylinder/plate structure. Journal of Sound and Vibration, Vol. 199, Issue 4, 1997, p. 629-643.

Publisher
Wu J. H., Chen H. L., An W. B. A method to predict sound radiation from a plate-ended cylindrical shell excited by an external force. Journal of Sound and Vibration, Vol. 237, Issue 5, 2000, p. 739-803.

Publisher
Wang Z. H., Xing J. T., Price W. G. A study of power flow in a coupled plate-cylindrical shell system. Journal of Sound and Vibration, Vol. 271, Issues 3-5, 2004, p. 863-882.

Publisher
Liang S., Chen H. L. The natural vibration of a conical shell with an annular end plate. Journal of Sound and Vibration, Vol. 294, Issue 4-5, 2006, p.927-943.

Publisher
Liang S., Chen H. L., Chen T., Wang M. Y. The natural vibration of a symmetric cross-ply laminated composite conical-plate shell. Composite Structures, Vol. 80, Issue 2, 2007, p. 265-278.

Publisher
Efraim E., Eisenberger M. Exact vibration frequencies of segmented axisymmetric shells. Thin-Walled Structures, Vol. 44, Issue 3, 2006, p. 281-289.

Publisher
Caresta M., Kessissoglou N. J. Free vibrational characteristics of isotropic coupled cylindrical-conical shells. Journal of Sound and Vibration, Vol. 329, Issue 6, 2010, p. 733-751.

Publisher
Kang J. H. Three-dimensional vibration analysis of joined thick conical-Cylindrical shells of revolution with variable thickness. Journal of Sound and Vibration, Vol. 331, Issue 18, 2012, p. 4187-4198.

Publisher
Qu Y., Chen Y., Long X., Hua H., Meng G. A modified variational approach for vibration analysis of ring-stiffened conical-cylindrical shell combinations. European Journal of Mechanics – A/Solids, Vol. 37, 2013, p. 200-215.

Publisher
Qu Y., Wu S., Chen Y., Hua H. Vibration analysis of ring-stiffened conical-cylindrical-spherical shells based on a modified variational approach. International Journal of Mechanical Sciences, Vol. 69, 2013, p. 72-84.

Publisher
Shakouri M., Kouchakzadeh M. A. Stability analysis of joined isotropic conical shells under axial compression. Thin-Walled Structures, Vol. 72, 2013, p. 20-27.

Publisher
Wu S., Qu Y., Hua H. Vibration characteristics of a spherical-cylindrical-spherical shell by a domain decomposition method. Mechanics Research Communications, Vol. 49, 2013, p. 17-26.

Publisher
Kouchakzadeh M. A., Shakouri M. Free vibration analysis of joined cross-ply laminated conical shells. International Journal of Mechanical Sciences, Vol. 78, 2014, p. 118-125.

Publisher
Ma X., Jin G., Xiong Y., Liu Z. Free and forced vibration analysis of coupled conical-cylindrical shells with arbitrary boundary conditions. International Journal of Mechanical Sciences, Vol. 88, 2014, p. 122-137.

Publisher
Shakouri M., Kouchakzadeh M. A. Free vibration analysis of joined conical shells: analytical and experimental study. Thin-Walled Structures, Vol. 85, 2014, p. 350-358.

Publisher
Su Z., Jin G., Ye T. Three-dimensional vibration analysis of thick functionally graded conical, cylindrical shell and annular plate structures with arbitrary elastic restraints. Composite Structures, Vol. 118, 2014, p. 432-447.

Publisher
Xie X., Zheng H., Jin G. Integrated orthogonal polynomials based spectral collocation method for vibration analysis of coupled laminated shell structures. International Journal of Mechanical Sciences, Vol. 98, 2015, p. 132-143.

Publisher
Tang D., Pang F., Wang Q., Yao X. Research on transmission loss of power flow through a finite V-shaped plate. Journal of Vibration Engineering, Vol. 29, Issue 1, 2016, p. 112-122.

Search CrossRef
Tang D., Wu G., Yao X., Wang C. Free vibration analysis of circular cylindrical shells with arbitrary boundary conditions by the method of reverberation-ray matrix. Shock and Vibration, 2016.

Publisher
Yao X., Tang D., Pang F., Li S. Exact free vibration analysis of open circular cylindrical shells by the method of reverberation ray matrix. Journal of Zhejiang University – Science A (Applied Physics and Engineering), Vol. 17, Issue 4, 2016, p. 295-316.

Publisher
Tang D., Sun L., Yao X., Yue X. Free vibration analysis of open circular cylindrical shells by the method of reverberation-ray matrix. Advances in Mechanical Engineering, Vol. 8, Issue 3, 2016, p. 1-21.

Publisher

Cited by

Dynamic responses of composite plate-shell coupled structures under moving excitations

(2024)

An analytical model for the analysis of vibration and energy flow in a clamped stiffened plate using integral transform technique

Hui Guo | Kai Zhang

(2024)

A unified vibration modeling of open cylindrical shell-rectangular plate coupling structures based on the dynamic stiffness method

(2023)

Propagation and attenuation characteristics of free flexural waves in multi-stepped periodic beams by the method of reverberation-ray matrix

Dong Tang | Liaoyuan Li | Zhongyu Zhang | Shuai Wu

(2021)

Theoretical and experimental modeling of beam-type flexural wave behaviours of orthogonally stiffened plates

Dong Tang | Wei Zhang | Liaoyuan Li | Xi Ye

(2021)

Free and forced vibration analysis of multi-stepped circular cylindrical shells with arbitrary boundary conditions by the method of reverberation-ray matrix

Dong Tang | Xiongliang Yao | Guoxun Wu | Yi Peng

(2017)

About this article

Received

04 March 2016

Accepted

28 June 2016

Published

15 August 2016

SUBJECTS

Modal analysis

DOI

https://doi.org/10.21595/jve.2016.16950

Keywords

plate/shell coupled structures

method of reverberation-ray matrix

free vibration analysis

Flügge thin shell theory

analytical wave form solution

Acknowledgements

This work is financially supported by National Natural Science Foundation of China (Grant Nos. 51479041, 51279038). The authors would like to express their profound thanks for the financial support and sincerely thank Miss Jingjing Yu for the scientific discussions and suggestions and the anonymous reviewers for the critical and constructive comments on this paper.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 02

An analytical model for the analysis of vibration and energy flow in a clamped stiffened plate using integral transform technique

Hui Guo, Kai Zhang

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2018 12 13

Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Jun Zhang, Tianyun Li, Xiang Zhu

Research article

2016 12 31

Free vibration solution of thick plate by using three-dimensional coupled thermoelastic theory

Huan He, Cheng He, Weimin Chen, Guoping Chen

D. Tang, X. Yao, and G. Wu, “Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix,” Journal of Vibroengineering, Vol. 18, No. 5, pp. 3117–3137, Aug. 2016, https://doi.org/10.21595/jve.2016.16950

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16950
UR  - https://doi.org/10.21595/jve.2016.16950
TI  - Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix
T2  - Journal of Vibroengineering
AU  - Tang, Dong
AU  - Yao, Xiongliang
AU  - Wu, Guoxun
PY  - 2016
DA  - 2016/08/15
PB  - JVE International Ltd.
SP  - 3117-3137
IS  - 5
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Tang_2016,
	doi = {10.21595/jve.2016.16950},
	url = {https://doi.org/10.21595/jve.2016.16950},
	year = 2016,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {5},
	pages = {3117--3137},
	author = {Dong Tang and Xiongliang Yao and Guoxun Wu},
	title = {Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]D. Tang, X. Yao, and G. Wu, “Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix,” Journal of Vibroengineering, vol. 18, no. 5, pp. 3117–3137, Aug. 2016, doi: 10.21595/jve.2016.16950.

Copy IEEE

Copied to clipboard!

Tang, Dong, Xiongliang Yao, and Guoxun Wu. “Free Vibration Analysis of Plate/Shell Coupled Structures by the Method of Reverberation-Ray Matrix.” Journal of Vibroengineering 18, no. 5 (August 15, 2016): 3117–37. https://doi.org/10.21595/jve.2016.16950.

Copy Chicago

Copied to clipboard!

Free vibration analysis of plate/shell coupled structures by the method of reverberation-ray matrix

Abstract

1. Introduction

2. Formulation

2.1. Force and moment resultants in a plate

2.2. Governing differential equations and the solutions of the plate

2.3. Force and moment resultants in an open circular cylindrical shell

2.4. Governing differential equations and solutions of the open circular cylindrical shell

2.5. Equation of natural frequencies for the plate/shell coupled structures

2.5.1. Scattering matrix

2.5.2. Phase matrix

2.5.3. Permutation matrix

2.5.4. Reverberation-ray matrix and the equation of natural frequencies

2.6. Searching algorithm for natural frequencies

3. Results and discussions

3.1. The box-type structure

3.2. The racetrack cylindrical shell

3.3. The ship hull structure

4. Conclusions

References

Cited by

About this article

Related Articles