Effect of pre-stress on natural vibration frequency of the continuous steel beam based on Hilbert-Huang transform

1. Introduction

The increasingly requirements are proposed for the span and space of the architectural structure, which thus promotes the wide application of the pre-stressed technology in architectural structure and its even more widespread employment in long-span bridges. For pre-stressed bridges, most loads of the bridge are undertaken by the pre-stressed system. And condition of the bridge is largely determined by its actual stress. Therefore, regular detections are necessary for the pre-stressed system of the bridge. However, in the operation process of the bridge, it is rather difficult to test the pre-stress value in the pre-stressed system through the regular methods [1-3].

The stress state and bearing capacity of the bridge can be reflected through the dynamic properties of the bridge structure, and hence the stiffness change of the structure would be caused by the loss of pre-stress, resulting in the simultaneous change of both structure and natural frequency of the bridge. Therefore, detection methods based on pre-stress loss concerning the natural frequency-based bridges were researched by many scholars. After the pre-stress tension within the bridge, the flexural rigidity of the beam would be improved greatly, thereby causing the change of the natural frequency of the beam. Therefore, the natural frequency of the bridge can be detected to further identify the pre-stress value. In the long-term operation of the bridge, the shrinkage of concrete and the pass of the overloaded vehicles may generate changes of the pre-stress value, even partial damage of the bridge [4, 5].

FFT method is widely applied in the time-domain signal processing method of the bridge, which can transfer time-domain signal to the frequency domain signal through the discrete Fourier algorithm, thus obtaining fundamental frequency information of the beam. However, such method cannot obtain the instantaneous frequency of beam within the acquisition period. Under the axial force of the pre-stressed steel strand, the natural vibration frequency of the beam is usually a time variable and only the analysis towards its instantaneous frequency can be significant. As a relatively new processing method for non-linear and unsteady signals, HHT departs from the characteristics of the original signal, decomposes the original signal into a series of intrinsic mode function (IMF) components through the empirical mode decomposition (EMD) method, and conducts Hilbert transformation for each IMF component, thus obtaining the Hilbert spectrum of energy distribution on time-frequency plane, breaking the limits of uncertainty principle, and expressing signal information on the time frequency plane more accurately.

As indicated in many references, the natural frequency of the bridge would be increased along with the rising pre-stress value, which is just contrary with the conventional mechanical theory [6]. Based on such phenomenon, new theories and methods were proposed by many scholars to explain the problem, such as Saiidi and Zhang, etc. Dependent on numerous experimental data, they raised their own stiffness-modified formula and frequency calculation formula of pre-stressed beams [7-9]. In most current researches, the inconsistency between such experimental phenomenon and traditional theory is still studied by virtue of the conventional FFT method, or the original theory equation is corrected based on the experimental result, which, nevertheless, does not capture an important indicator of beam fundamental frequency changes that are generated by the variations of pre-stress value, namely instantaneous frequency. As can be seen from the above description, new methods and tools should be used to analyze and study such problem deeply. However, along with the variation of pre-stress value, small changes of instantaneous frequency of pre-stress value can be captured through the characteristics of HHT method, thereby obtaining a more reliable result. Therefore, the paper attempted to study the relationship between the pre-stress value of continuous beams and the fundamental frequency based on HHT method.

Due to the failure acquisition of instantaneous frequency of the structure, FFT method cannot obtain the relationship between the pre-stress value and natural frequency currently. The continuous steel beam with the curvilinear reinforcement was chosen as the research object in the paper, dynamic detection method was applied to conduct dynamic tests of pre-stressed simply supported beams and HHT method was relied for data analysis, so as to study the relationship between the pre-stress value and natural frequency of continuous steel beam, targeting at providing theoretical guidance for the detection of pre-stress value in actual engineering.

2. Analytical method of vibration frequency of beam

The beam was considered as an isotropic material based on the traditional mechanics theory. The calculation equation regarding the natural frequency ${\omega }_n$ of simply supported beam was obtained as below under the compression state of both ends of the beam [10, 11]:

wherein, $n$ is a positive integer; $l$ indicates the net span of the beam; $N$ expresses the axial pressure suffered by both ends of the beam; $E_b{I}_b$ means the flexural rigidity of the beam; and $\rho A$ demonstrates the partial quality of the beam.

As thought in traditional mechanics theory, the natural vibration frequency of objects would be reduced under the action of stress and increased under the action of tension. Therefore, the natural frequency of simply supported beams would be reduced with the rising pre-stress on both ends of the beam, as known from Eq. (1). However, from the existing test results, the prestress of prestressed beams was shown completely opposite result with the natural frequency of beams. Based on this experimental phenomenon, new ways should be sought necessarily to solve this problem, and new theories and methods were proposed by many scholars to explain the problem. Dependent on numerous experimental data, Saiidi and Zhang Yaoting raised their own stiffness-modified formula and frequency calculation formula of pre-stressed beams.

The most commonly used analytical methods regarding the fundamental frequency of pre-stressed beams include FFT method and finite element analysis method. After the application of pre-stress in the steel beam, the overall vibration turns into the vibration of a time-varying system, and changes of the frequency are difficult to be obtained through the conventional frequency domain analysis method [12, 13]. Based on the dynamic analysis regarding the linear elasticity of the finite element model, the pre-stress is usually treated as an external load and applied on both ends of the beam, while the stiffness matrix and mass matrix of the beam itself cannot be changed. Therefore, the relationship between the pre-stress and fundamental frequency of the beam cannot be distinguished.

For better distinction of the relationship between the pre-stress and natural vibration frequency within the beam, a new analytical method of instantaneous frequency was introduced here, namely Hilbert-Huang Transform method. In the method, the original signal was firstly decomposed into IMF components based on EMD; then each IMF was made HHT transformation to obtain Hilbert spectrum of signals, which could describe the changes and distribution of structural frequency over time, namely the instantaneous frequency of the beam. After the elimination of end effects at both ends, the simply supported beam was made a linear fitting for the instantaneous frequency, thus obtaining the first-order frequency of the beam.

3. Dynamic test of pre-stressed continuous steel beam model

3.1. Pre-stressed continuous steel beam model

Q235 was applied in the column beam of the pre-stressed continuous steel beam model. To simulate the pre-stressed rebar in curvilinear placement within the beam, the vertical stiffening rib was placed in the abdomen on both sides of the model, with the total length of 5.0 m. The three-span continuous beam had the span of 1.6 m+1.6 m+1.6 m, whose experimental model was shown in Fig. 1. Three supports were placed along the beam length: a fixed hinge support was set in the middle, and movable hinge supports were arranged on both sides. The fixed hinge support can be realized by fixing the main beam through roller welding on the steel plate and by four threaded rods. In the movable hinge supports, rollers and steel plates were not welded together; instead, the steel plates, rollers and main beam were fastened directly through four threaded rods. The support was fastened on the steel beam base through threaded rods, and the steel beam bases were fixed on the foundation through anchorage bolts.

Fig. 1General arrangement diagram of continuous steel beam (unit: mm)

CF092 magnetoelectric acceleration sensors were applied in the paper and arranged in the points corresponding to the continuous two spans or three-spans. The sensor was possessed with an extremely low low-frequency response and high sensitivity, which showed significant effect in safety testing of the bridge and earth pulsating test and required passive servo and no power supply. The measurement and analysis systems of TST3827 static and dynamic signals were applied for data collection.

3.2. Application and control method of pre-stress

The pre-stressed steel strand within the beam was simulated through two strips of 7×7-304# stainless steel wirerope with the diameter of 2 mm, which were fixed at ends of beam through corresponding threaded bolts. In the experiment, threaded bolts at both ends of beam could be adjusted to achieve the modulation of wirerope tension and thereby fulfill the adjustment of prestress value of beam. The steel strand passed through the holes in vertical stiffening ribs of the beam, which was not fixed with the steel beam in its middle and was not contacted with the steel beam under the tension condition. The prestress value was tested through the tension sensor, and the tension sensor was connected with the steel wirerope in series through the ring with roller. The wirerope, tension sensor and prestressed control devices were shown as Fig. 2.

Fig. 2Anchor device and tension sensor

3.3. Experimental program

The experiment herein was mainly to study the relationship between the pre-stress value of the continuous beam and the natural frequency of the beam. On the basis of the above experimental model, the curvilinear placement of prestressed steel wirerope was applied and the prestressed steel strand was laid in the tension places of the beam. During the loading of prestress, the tensions of 0 N, 200 N and 400 N were applied in the steel wire-rope as shown in Table 1, respectively, so as to simulate different prestress values. After loading of each level of load, the hammering method was employed and excited at 1/6 place of a continuous steel beam, and the beam vibration signal was acquired through the acceleration sensor on beam, whose situ model testing was shown in Fig. 3.

Fig. 3Situ model testing

Table 1Experimental conditions

Item No.	Prestressed reinforcement position	Prestress value / N	Fundamental frequency experiment
SCB	Curvilinear placement	0 200 400	Hammering method tests and collects acceleration signal

4. Analysis of experimental result

After the application of different pre-stresses in steel wire-rope of beam, in accordance with the experimental programs, the acceleration signals of the steel beam were collected under the hammering action, the acquired signals were given the filtering process, and finally the data was made an analysis on the basis of FFT and HHT methods, respectively.

4.1. Analytical result based on FFT method

The collected acceleration signal of the beam was analyzed through the commonly used FFT analytical method. The spectral curves of the beam were obtained under different prestresses. Herein, the 4th acceleration sensor in the midspan of the continuous beam was applied to collect the signal for analysis, as shown in Fig. 4.

Fig. 4FFT-based spectrum of beam

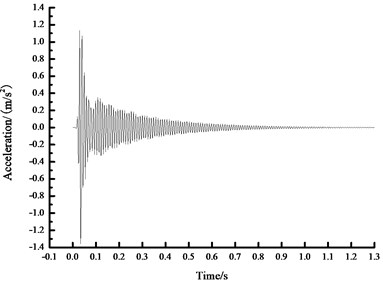
a) Time history curve of $T=$ 0 N acceleration

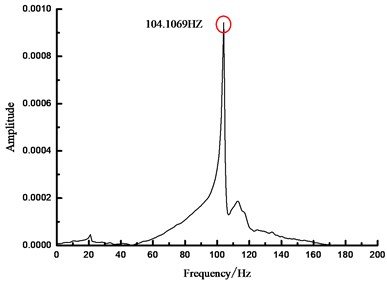
b)$T=$ 0 N spectrum

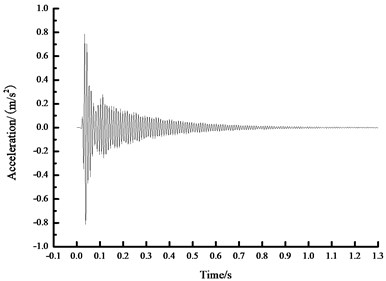
c) Time history curve of $T=$ 200 N acceleration

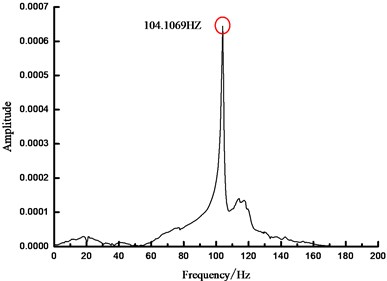
d)$T=$200 N spectrum

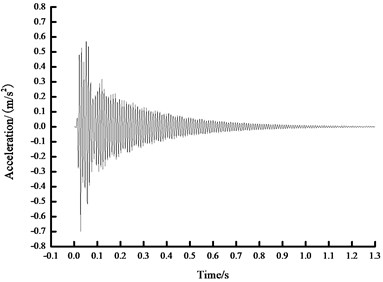
e) Time history curve of $T=$ 400 N acceleration

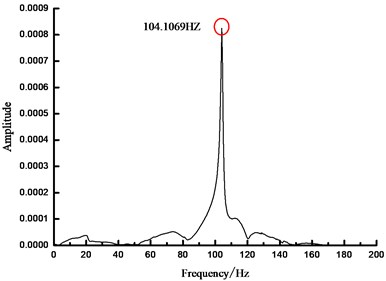
f)$T=$400 N spectrum

As seen from Fig. 4, based on FFT analytical method, the analytical results concerning the natural vibration frequency of steel beam were unchanged under different prestress states, namely 104.1069 Hz. In another word, FFT analytical method was insensitive to the prestress value in the prestressed steel beam, which cannot obtain the relationship between the prestress within beam and the fundamental frequency. Therefore, other methods are necessary to carry out more in-depth analysis.

4.2. Analytical result based on HHT method

HHT analytical method was programmed through MATLAB software. The same acceleration signals of steel beams were re-analyzed based on HHT analytical method herein, which could gain the natural vibration frequency of the steel beams under various operating conditions. The pre-stressed condition of $T=$400 N was taken as the example and described based on HHT method in the paper.

The original signal was filtered and then decomposed into IMF components on the basis of EMD. Herein, the first 4 IMF components were listed as shown in Fig. 5.

Fig. 5IMF decomposed by EMD method

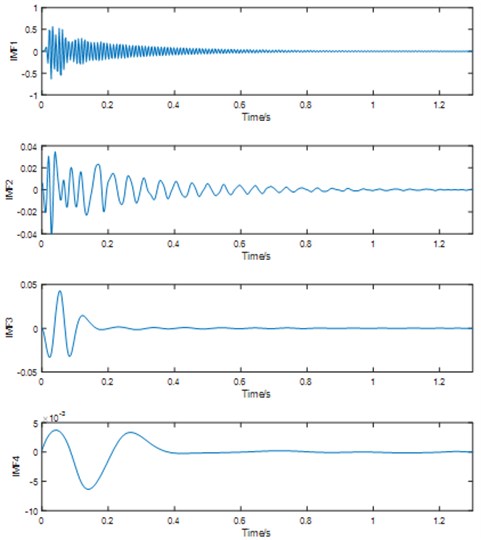
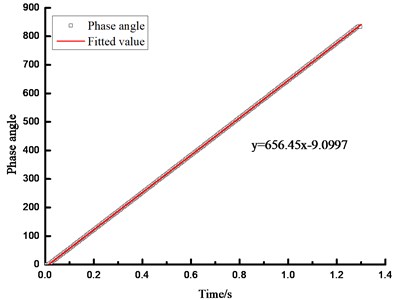
The first IMF component was made the HHT transformations to obtain its instantaneous frequency and phase angle. Among them, the specimen can be derived through the phase angle to obtain the instantaneous frequency of the beam in the vibration process. The instantaneous frequency of the beam was shown in Fig. 6 under the condition of $T=$400 N, and its phase angle was shown in Fig. 7.

It was indicated from Fig. 7 that a good linear relationship was presented in the phase angle of IMF1, which was more consistent with the linear equation of the fitting line. At this time, the fundamental frequency of the beam was:

2

$f=\frac{656.45}{2\pi }=104.4773.$

Based on same methods and procedures, the fundamental frequencies of the beam were 104.0046 Hz, 104.2381 Hz and 104.4773 Hz respectively under the stress values of 0 N, 200 N, 400 N.

Fig. 6Instantaneous frequency

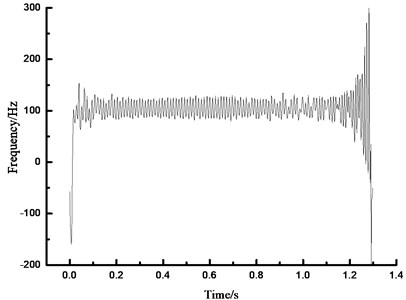
Fig. 7Phase angle fitting line

4.3. Comparison and analysis of results

The fundamental frequency result of the prestressed beams was obtained and collected on the basis of FFT and HHT analytical methods, as shown in Fig. 8. It was indicated that, along with the prestress value, the fundamental frequency changes of the beam cannot be analyzed through FFT. Under different prestress effects, no changes were occurred regarding the analytical result concerning the fundamental frequency of the beam; as shown from the analytical result of HHT method, the fundamental frequency of the beam was gradually enlarged along with the rising prestress value, but not entirely linear growth; in the absence of prestress state, the fundamental frequency error was 0.098 % under the two analytical methods, thus indicating the strong credibility of analytical results.

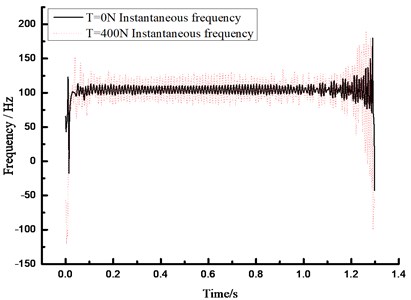
The instantaneous frequency of the structure could be obtained due to one biggest characteristic of HHT analytical method, namely the relationship between frequency and time. After analyzing the relationship between the prestress and fundamental frequency, the instantaneous frequency spectrums were compared under two conditions of $T=$0 N and $T=$400 N so as to understand the relationship between the prestress and instantaneous frequency deeply, as shown in Fig. 9. It could be found that the magnitude of the beam frequency would be increased along with the rising prestress value of the beam.

Fig. 8The fundamental frequency of different analysis method

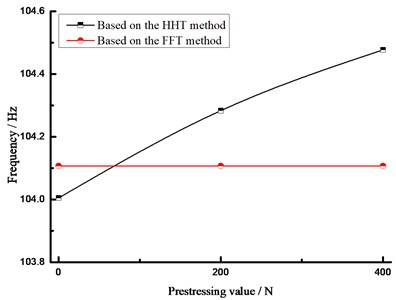
Fig. 9Instantaneous frequency-time spectrum under different conditions

From the above analysis, the natural vibration frequency of the prestressed continuous steel beam was a variable with a certain period of time. The relationship between the prestress and frequency was difficult to be gained through the conventional FFT analytical method, which was also an important reason of unable correct analysis in some previous researches. Such problem could be better solved through HHT analytical method.

5. Numerical simulation

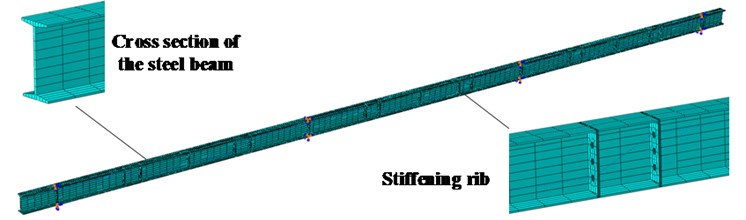
ABAQUS software was applied for modeling of the mentioned model. Among them, Solid element was applied in the steel beam and intermediate stiffening ribs, Truss element was employed in the pre-stressed steel strand, and two parts were connected through MPC. There were a total of 14065 elements in the model. The corresponding positions of the beam support were constrained its corresponding displacement and rotation, and the finite element model of the whole structure was shown in Fig. 10.

Fig. 10Finite element model

The finite element software was possessed with the modal analysis module, which nevertheless was based on the conventional mechanics analysis method. Namely, in the analytical result, the fundamental frequency of the beam would be reduced under the axial pressure action, which was inconsistent with the actual test results. Therefore, the first several order vibration modes and fundamental frequency were directly extracted on the direct basis of the analytical method built in the software, which could not gain the relationship between the prestress value and fundamental frequency of the prestressed steel beam. Hence, the hammering method consistent with the actual experiments was applied during analyzing the numerical simulation in the paper. After extracting the acceleration signal of the beam, the previous HHT method was applied for analysis, so as to obtain accurate analytical results. In the numerical model, the hammering method was used by adding 100 N concentrated load in the left midspan at 0.11 s moment suddenly, the analysis of 2 s instantaneous condition was conducted for the structure, and the acceleration curve in the mid-span of the continuous beam was extracted. And the sampling frequency was set to 500 Hz, as shown in Fig. 11.

Similarly, HHT method was applied to analyze the collected data. Consequently, the natural frequencies 105.5485 Hz, 105.8049 Hz and 106.0661 Hz of the numerical model were acquired under different pre-stress values, which were compared with the actual measurement values, as shown in the following table. It could be seen that the error of the actual measurement values and numerical simulation values regarding HHT analytical method was within 1.52 %, and their values also showed the same patterns and trends. Namely, the fundamental frequency of the prestressed continuous steel beam was increased along with the rising prestress value.

Fig. 11The acceleration time history curve in the midspan

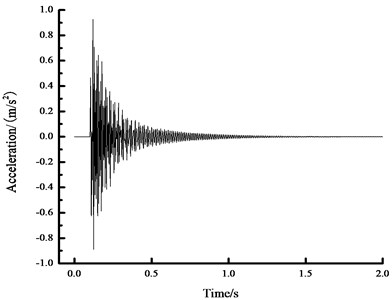
a) Time history curve of $T=$ 0 N acceleration

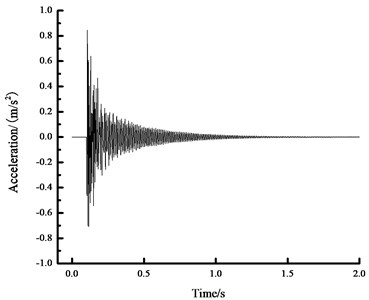
b)$T=$ 0 N spectrum

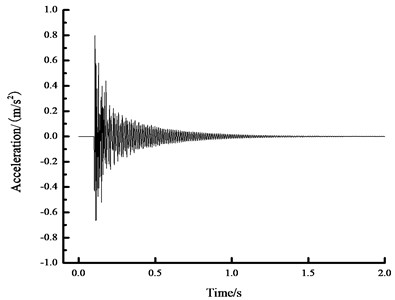
a) Time history curve of $T=$ 400 N acceleration

6. Conclusions

The pre-stressed continuous steel beam model was tested to study the relationship between the fundamental frequency and pre-stress value of the pre-stressed continuous steel beam. The following main conclusions can be obtained through the analytical result of different spectral analysis methods:

1) The relationship between the fundamental frequency and pre-stress value of the pre-stressed beam cannot be well explained by the traditional mechanics theory, whose theoretical value was just contrary to the experimental value.

2) The instantaneous frequency of the structure and the pre-stress value changes with its fundamental frequency cannot be obtained through FFT method.

3) The instantaneous frequency of the beam could be captured better through HHT spectrum analytical method, and the analytical result of the method was rather sensitive to the pre-stress value, which truly reflected the relationship between the beam frequency and pre-stress value;

4) The natural vibration frequency of the pre-stressed beam was increased along with the rising pre-stress value, and meanwhile the vibration amplitude involving instantaneous frequency of the beam will also be enhanced correspondingly.

5) The numerical simulation model was also built to calculate the corresponding results and compared with those of HHT method. The relative small error was presenting in the experimental result and numerical simulation result, thus indicating the reliability and accuracy of the HHT method.