Abstract
To effectively extract rolling bearing fault feature under variable conditions, a hybrid method based on order tracking and EEMD is proposed in this paper. This method takes the advantages of order tracking, ensemble empirical mode decomposition and 1.5 dimension spectrum. Firstly, order tracking is used to transform the time domain non-stationary vibration signal to angular domain stationary signal. Secondly, ensemble empirical mode decomposition is performed to decompose the angular domain stationary signal into a series of IMFs, and select the IMF in which the largest vibration energy occurs as the characteristic IMF. Thirdly, 1.5 dimension spectrum is further employed to analyze the characteristic IMF, and extract the fault features from background noise. The proposed method is applied to analyze the experimental vibration signals, and the analysis results confirm the effectiveness of the proposed method under variable conditions.
1. Introduction
Rolling bearing is widely used in rotating machinery, such as gas turbines, generators, and aircraft engines. Therefore, the fault diagnosis of rolling bearing is of great significance in industry and has attracted more and more attention.
Most researches usually consider the same rotating speed or rotating speed slight change as stationary processes. In fact, rolling bearing frequently is under variable conditions especially during the speeding up or speeding down [1]. Since traditional techniques in diagnosis mostly cater for stationary processes, it therefore will not produce satisfactory results when applied to nonlinear systems or variable conditions [2]. Nowadays, more and more researchers focus on variable conditions problem. Zhao [3] et al. introduced an instantaneous speed estimation method for fault detection. Amir [4] et al. extracted the feature based on local Gaussian correlation function of wavelet coefficients. Wang [5] et al. used wavelet and correlation filtering to identify fault feature.
The vibration signals measured from rolling bearing usually are complex and non-stationary with heavy background noise, and the useful characteristics of rolling bearing faults are hidden in the background noise. Especially in the early stages of fault development, the characteristic information is too weak to detect [6-7]. So the detection of the characteristics of weak faults in rolling bearing from the background noise is still a big challenging task. Order tracking is an important method for fault diagnosis under variable conditions [8-12]. Order tracking has been further developed, such as Gabor order tracking [13]. Ensemble empirical mode decomposition has many advantages and has been applied in many scientific fields [14-17]. Get several intrinsic mode functions by EEMD, then the vibration fault feature was separated by enveloping demodulation method [18]. 1.5 dimension spectrum can extract fault characteristic frequencies from background noise or weak signal [19].
In this paper, a novel hybrid method based on order tracking, EEMD and 1.5 dimension spectrum is proposed in order to extract rolling bearing fault feature under variable conditions effectively, which combines the advantages of order tracking, EEMD and 1.5 dimension spectrum. Order tracking is used to convert the non-stationary vibration signals from time domain to angular domain stationary signal. EEMD decomposes the angular domain stationary signal into a series of narrow frequency band IMFs, and enhances the fault characteristic components in the characteristic IMF. 1.5 dimension spectrum is further performed on the characteristic IMF vibration signal and the background noise in the characteristic IMF is restrained, and the fault feature is extracted. The proposed method is applied to rolling bearing fault feature extraction under variable conditions to verify the effectiveness. The results confirm that it performs better than Hilbert transform demodulation method. The rolling bearing outer raceway fault characteristic order is effectively extracted.
The rest of this paper is organized as follows. The basic rationale of order tracking, EEMD and 1.5 dimension spectrum is presented in Section 2. The proposed method for Rolling bearing fault feature extraction under variable conditions is discussed in Section 3. The experimental validation is presented in Section 4. Finally, conclusion is given in Section 5.
2. Basic rationale
2.1. Order tracking
Order tracking is widely applied to analysis non-stationary vibration signal in the varying-speed condition, which adopts equal-angle resample method to remove the non-stationary characteristics. The process of order tracking is as follows [9].
Assuming that the shaft is under a constant acceleration condition, shaft angle can be represented with a quadratic equation given by:
where , , are unknown coefficients, they can be calculated by three successive keyphasors’ arrival times (, , ). The shaft angle increments is 360°:
Substituting Eq. (2) into Eq. (1), solve the equations, and are obtained as follows:
Then resample time is calculated:
where is the equal-angle resample spacing in angular domain, and is the integer.
After the resample time is obtained, the corresponding vibration amplitude at is calculated with interpolation. By this means, the non-stationary vibration signal is converted from time domain into angular domain stationary signal with equal-angle resample method.
More details about order tracking are discussed in reference [9].
2.2. EEMD method
EEMD is a nonlinear signal processing method. EEMD is a new signal processing method proposed by Huang on the basis of EMD, which overcomes the problem of modal aliasing. The EEMD algorithm can be described as follows [14-17]:
(1) Initialize the number of ensemble M and the amplitude of the added white noise.
(2) The signal added th white noise is obtained:
where is original vibration signal, and represents the noise-added signal of the th trial.
(3) Repeat step (1) and (2) with independent white noise series for hundreds epochs.
(4) Calculate the mean of corresponding IMFs as the final output pattern.
2.3. 1.5 dimension spectrum
1.5 dimension spectrum can eliminate background noise and provide more information than classical methods such as envelope spectrum analysis [19].
1.5 dimension spectrum is defined as the diagonal slice spectrum of the third-order cumulant of a signal , and it is denoted as:
where is Fourier transform of , is complex conjugate of .
3. The proposed method
Under variable conditions, rolling bearing characteristic orders are calculated as follows [20, 21]:
where is the shaft spin order. , , and are rolling element diameter, pitch diameter, rolling element contact angle and number of rolling elements, respectively. and are the outer raceway fault characteristic order and the inner raceway fault characteristic order, respectively.
In this paper, to effectively extract fault features under variable conditions, we employ order tracking to convert the time domain non-stationary vibration signal to angular domain stationary signal, EEMD is used to refine the vibration characteristics, and 1.5 dimension is further adopted to extract the fault features. The procedures of the proposed method are as follows:
1) Get the time domain sample signal from sampling the vibration acceleration signal and the pulse signal at the same time;
2) Set threshold value of the pulse signal in order to get the pulse arrival time;
3) According to the pulse time it can be drawn up speed change diagram;
4) According to the velocity determine the highest order and set angle domain sampling points;
5) Use three successive pulse arrival times in order to calculate unknown coefficients ;
6) Through determine the angle increment , then get the corresponding point in time;
7) According to , interpolate the vibration acceleration signal into corresponding place and complete the angle domain resampling;
8) After the angle domain resampling, deal with EEMD to select characteristic IMF;
9) Perform 1.5 dimension spectrum to analyze the characteristic IMF and extract the weak fault feature.
10) The flowchart of the proposed method is presented in Fig. 1.
Fig. 1The flowchart of the proposed method
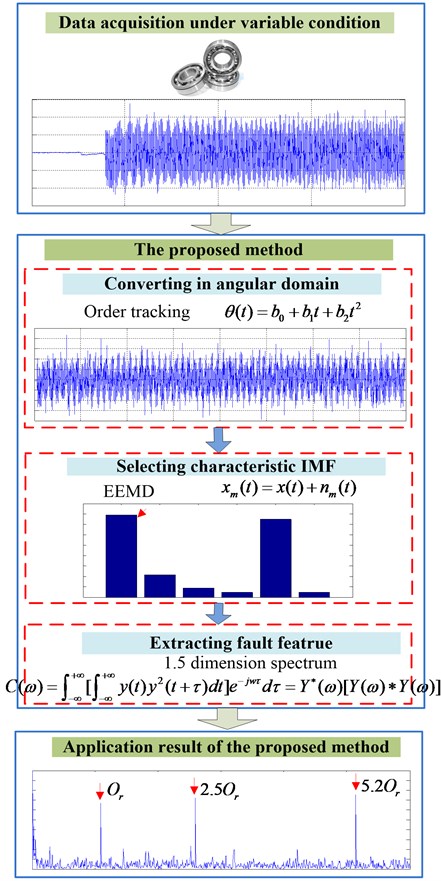
4. Experimental validation
Rolling bearings are the key parts of rotating machinery. In this paper, rolling bearing experimental vibration signal under variable condition is used to verify the effectiveness of the proposed method. Fig. 2 is the multi-function experimental setup, which consists of motor, testing rolling bearing, accelerometer, photoelectric sensor and other components. The experimental setup is driven by the motor. The testing rolling bearing with outer raceway fault was mounted at the shaft end, which is shown in Fig. 3. The photoelectric sensor picks up the speed pulse signals.
The experimental setup operated in speeding up to simulate rolling bearing under variable condition. The rotor speed rose from 0 to 420 rpm, and the motor is used to change the rotor speed. The sampling frequency was 10000 Hz, and the sampling time was 20 seconds.
Fig. 2Multi-function experimental setup

Fig. 3Rolling bearing outer raceway fault

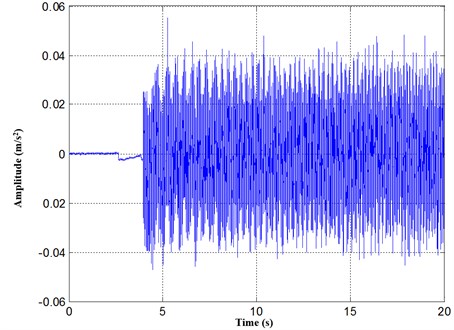
The vibration signal of rolling bearing is picked up with accelerometer, and it is shown in Fig. 4. From Fig. 4, the rolling bearing vibration signal in time domain during speeding up is complex, and no more fault information can be obtained.
The rotating speed of rolling bearing during speeding up is illustrated in Fig. 5. From Fig. 5, the speeding up of rolling bearing is a non-stationary process, and the speed changes violently.
Fig. 4Vibration signal of rolling bearing
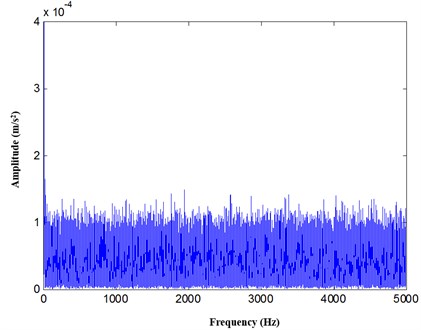
The FFT spectrum of the vibration signal is presented in Fig. 6. The frequency components are abundant, and we cannot find the useful characteristic frequency components. From Fig. 6, it shows that the traditional FFT spectrum analysis is not suitable for rolling bearing fault feature extraction under variable condition.
Fig. 5Rolling bearing rotating speed during speeding up
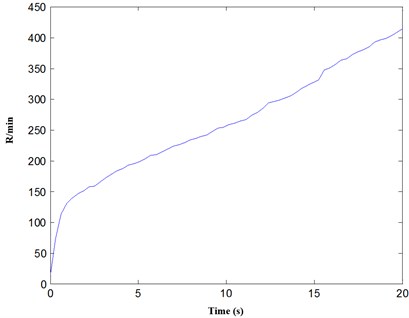
Fig. 6Vibration signal spectrum
To extract the fault feature, the vibration signal is transformed from time domain to angular domain with order tracking, and the result is illustrated in Fig. 7.
To further extract the rolling bearing fault feature, EEMD is performed to decompose the angular domain vibration signal into a series IMFs. The vibration energy of each IMF is calculated, and the results are illustrated in Fig. 8. From Fig. 8, the largest vibration energy occurs in the first IMF, and the outer race fault feature of rolling bearing is enhanced in the first IMF, so the first IMF is selected as the characteristic IMF for rolling bearing outer race fault.
Fig. 7Angular domain vibration signal
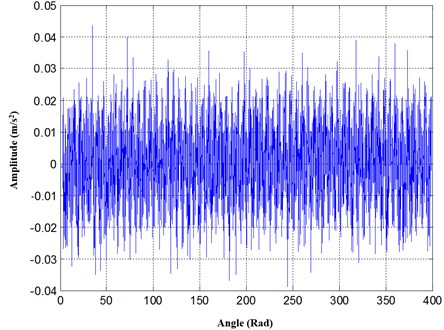
Fig. 8EEMD IMFs vibration energy
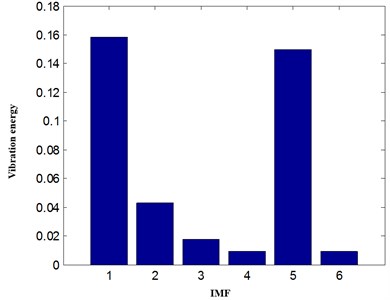
1.5 dimension spectrum is further used to analyze the first IMF, and the result is illustrated in Fig. 9. Based on the shaft spin order and the geometric parameters of the testing rolling bearing, the outer raceway fault characteristic order is calculated with Eq. (7), which is . In Fig. 9, there exist three clear feature orders, which are , and , respectively. The outer raceway fault characteristic order is obviously extracted, which coincide with the outer raceway fault of the testing rolling bearing. The proposed method well reveals under variable condition.
Fig. 9The analysis result with the proposed method
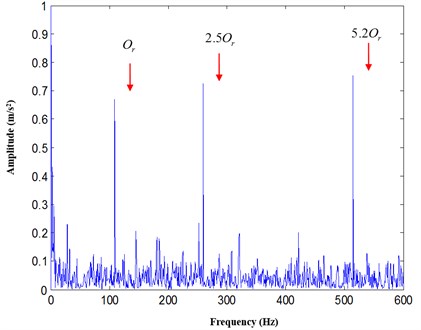
For comparison, Hilbert transform demodulation method is also used to analyze the first IMF, and the result is illustrated in Fig. 10. In Fig. 10, there are no obvious feature orders, and outer raceway fault characteristic order is not extracted. Hilbert transform method fails to reveal the outer raceway fault of the testing rolling bearing.
Fig. 10The analysis result with Hilbert transform demodulation
5. Conclusions
In this paper, we have proposed a hybrid method based on order tracking and EEMD for rolling bearing fault feature extraction under variable conditions. Order tracking is adopted to transform the non-stationary vibration signal to angular domain stationary signal, EEMD is used to select the characteristic IMF and 1.5 dimension spectrum is further employed to extract fault characteristic order.
The proposed method is applied to analyze the rolling bearing vibration signal under variable condition, and the result confirms that it performs better than other method and effectively extracts rolling bearing outer raceway fault characteristic order.
References
-
Ye Tian, Jian Ma, Chen Lu, Zili Wang Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mechanism and Machine Theory, Vol. 90, 2015, p. 175-186.
-
Man Shan Kan, Andy C. C. Tan, Joseph Mathew A review on prognostic techniques for non-stationary and non-linear rotating systems. Mechanical Systems and Signal Processing, Vol. 62, 2015, p. 1-20.
-
Zhao Ming, Lin Jing, Wang Xiufeng, et al. Fluctuation analysis of instantaneous angular speed based on digital differentiator and its application in vibration source identification. Journal of Mechanical Engineering, Vol. 48, Issue 22, 2012, p. 1-6.
-
Amir Hosein Zamanian, Abdolreza Ohadi Gear fault diagnosis based on Gaussian correlation of vibrations signals and wavelet coefficients. Applied Soft Computing, Vol. 11, 2011, p. 4807-4819.
-
Wang Shibin, Huang Weiguo, Zhu Z. K. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 1299-1320.
-
Zhang ChunLin, Li Bing, Chen BinQiang, Cao HongRui, Zi YanYang, He ZhengJia Weak fault signature extraction of rotating machinery using flexible analytic wavelet transform. Mechanical Systems and Signal Processing, Vol. 64, 2015, p. 162-187.
-
Li Feng, Wang Jiaxu, Chyu Minking K., Tang Baoping Weak fault diagnosis of rotating machinery based on feature reduction with supervised orthogonal local fisher discriminant analysis. Neurocomputing, Vol. 168, 2015, p. 505-519.
-
Remond Didier, Mahfoudh Jarir From transmission error measurements to angular sampling in rotating machines with discrete geometry. Shock and Vibration, Vol. 9, 2005, p. 1-13.
-
Fyfe K. R., Munck E. D. S. Analysis of computed order tracking. Mechanical Systems and Signal Processing, Vol. 11, Issue 2, 1997, p. 187-205.
-
Bossley K. M., Mckendrick R. J., Harris C. J., Mercer C. Hybrid computed order tracking. Mechanical Systems and Signal Processing, Vol. 13, Issue 4, 1999, p. 627-641.
-
Coats Michael D., Randall Robert B. Single and multi-stage phase demodulation based order-tracking. Mechanical Systems and Signal Processing, Vol. 44, 2014, p. 86-117.
-
Borghesani P., Pennacchi P., Chatterton S., Ricci R. The velocity synchronous discrete Fourier transform for order tracking in the field of rotating machinery. Mechanical Systems and Signal Processing, Vol. 44, 2014, p. 118-133.
-
Pan C. M., Liao S. W., Chiu C. C. Improvement on Gabor order tracking and objective comparison with Vold-Kalman filtering order tracking. Mechanical System and Signal Processing, Vol. 21, 2007, p. 653-667.
-
Amirat Yassine, Choqueuse Vincent, Benbouzid Mohamed EEMD-based wind turbine bearing failure detection using the generator stator current homopolar component. Mechanical Systems and Signal Processing, Vol. 41, 2013, p. 667-678.
-
Wang Hongchao, Chen Jin, Dong Guangming Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Applied Acoustics, Vol. 77, 2014, p. 195-203.
-
Chen Xi-hui, Cheng Gang, Shan Xian-lei, Hu Xiao, Guo Qiang, Liu Hou-guang Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement, Vol. 73, 2015, p. 55-67.
-
Xue Xiaoming, Zhoun Jianzhong, Xu Yanhe, Zhu Wenlong, Li Chaoshun An adaptively fast ensemble empirical mode decomposition method and its applications to rolling element bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 62, Issue 63, 2015, p. 444-459.
-
Qi Xiaoxuan, Yuan Zhonghu, Han Xiaowei Diagnosis of misalignment faults by tacholess order tracking analysis and RBF networks. Neurocomputing, Vol. 169, 2015, p. 439-448.
-
Jiang Hongkai, Xia Yong, Wang Xiaodong Rolling bearing fault detection using an adaptive lifting multiwavelet packet with a 1.5 dimension spectrum. Measurement Science and Technology, Vol. 24, Issue 12, 2013, p. 125002-125012.
-
Wang Tianyang, Liang Ming, Li Jianyong, Cheng Weidong Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis. Mechanical Systems and Signal Processing, Vol. 45, 2014, p. 139-153.
-
Guo Yu, Liu Tingwei, Na Jing, Rongfong Fung Envelope order tracking for fault detection in rolling element bearings. Journal of Sound and Vibration, Vol. 331, 2012, p. 5644-5654.
Cited by
About this article
This research is supported by the National Natural Science Foundation of China (No 51475368) and Shanghai Engineering Research Center of Civil Aircraft Health Monitoring Foundation of China (No GCZX-2015-02).
