The influence of damping coating geometrical-material parameters on helical spring longitudinal vibration amplitudes

2.1. Equivalent rod model

The equivalent rod model with suitable dynamic parameters can be utilised when considering the longitudinal vibrations of coated helical springs. The effects connected with damping can be initially omitted, as damping does not affect the normal mode shapes, and due to the relatively low damping obtained by elastomeric coatings, its influence on natural frequencies is small. Thus, the wave equation of undamped longitudinal vibrations of equivalent rod takes a conventional for $m$:

where $m$ denotes the linear density of equivalent rod, whereas $\gamma$ denotes an equivalent compression rigidity [8]:

where: $n$ – number of active coils, $L$ – current active spring height, $R$ – half of the nominal diameter of the spring, $G_w$ and $G_c$ – shear modulus of the spring wire and coating material respectively, $J_w$ and $J_c$ are area moments of inertia of the wire and coating cross-sections respectively.

2.2. Amplitudes of resonant longitudinal spring vibrations

The first four normal longitudinal modes of a clamped-clamped coated helical spring as well as plots of the displacement amplitudes of equivalent rod modelling for the spring are presented in Fig. 1.

Fig. 1The first four longitudinal natural modes of a clamped-clamped coated helical spring with corresponding plots of displacement amplitudes of equivalent rod

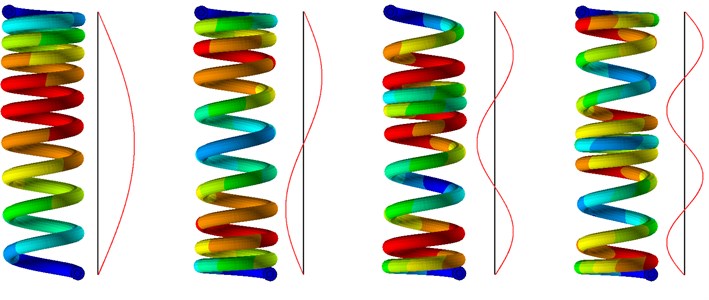
Under the initial assumption that both ends of the spring are fixed, one can write the stationary solution of Eq. (1) and the time independent factor $X_i\left(x\right)$ of this solution, which describes the amplitudes of longitudinal vibrations of equivalent rod modelling for the considered spring:

where $i=$ 1, 2, 3,... denotes the number of the natural longitudinal frequency ${\omega }_i$.

Knowing the shape of the vibration mode, one can calculate the maximal elastic energy stored in the spring in resonance conditions as a function of the maximal amplitude $A_i$ and, subsequently using the definition of the specific damping capacity $\xi$, the energy dissipated during one period of vibrations can be determined. According to this definition [9], energy dissipated during the cycle $U_{Dj}$ is equal to the maximal potential energy $U_j$ of the vibratory system within one cycle multiplied by the specific damping capacity$\xi$. In the case of a spring with a damping coating on its wire, the equivalent relative energy dissipation $\xi$ can be written in the form [10]:

where: ${\xi }_w$ is the specific damping capacity of the spring wire material, whereas ${\xi }_c$ is the specific damping capacity of the coating material. Longitudinal deformations of the spring are connected mainly with the twisting of the wire and the coating, thus the energy dissipated by the spring $U_{di}$ during one period of vibrations amounts to:

where: $S$ is the active length of the coating and the spring wire, $s$ – the coordinate along the spring wire axis, $\delta$ – the lead angle of the helix.

Giving up the initial assumption that both ends of the spring are clamped and assuming in return that one end of the spring (at $x=$ 0) is moving in accordance with the equation $u(x=0,t)=a\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$ and only the second end of the spring (at $x=L$) is clamped, the work $W_i$ performed by the vibrating support on the spring can be determined. This work can be expressed in the following form:

It should be mentioned that in resonance conditions, when $\omega ={\omega }_i$, there is a phase shift between the driving oscillation and vibrations equal to one quarter of the period, thus the function $u_i\left(x,t\right)$ appearing in Eq. (6) has the following form:

Comparing the energy dissipated during one period of vibrations $U_{Di}$ (Eq. (5)) with the work $W_i$ performed on the spring during this period (Eq. (6)), after transformations we obtain the ratio of the maximal amplitude $A_i$ to the amplitude of the spring end (at $x=$0) displacement $a$:

The relationship Eq. (8) therefore allows the maximal vibration amplitude of the spring with a damping coating on its wire to be determined, when the amplitude of driving oscillations is given.

2.3. Numerical examples

Fig. 2 presents the ratio between the maximal resonant vibration amplitude $A_i$ of the spring with a damping coating to the maximal resonant vibration amplitude $A_{nci}$ of the same spring but without a damping coating, under the assumption that the excitation amplitude $a$ is the same in both cases as a function of the coating material shear modulus $G_c$ and the ratio of coating and wire diameters. It was assumed that ${\xi }_w=$0.01 and ${\xi }_c=$0.4.

Fig. 2The ratio of amplitudes Ai/Anci as a function of coating material shear modulus Gc and the ratio of coating and wire diameters dc/dw

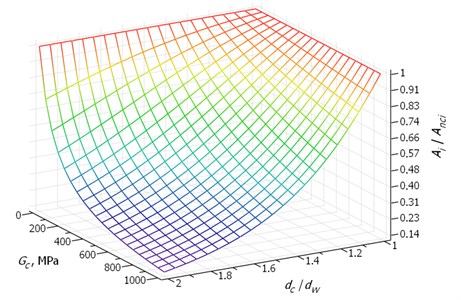
Fig. 3 presents the ratio of amplitudes $A_i/A_{nci}$ as a function of coating material shear modulus $G_c$ and the coating material specific damping capacity ${\xi }_c$ under the assumption that $d_c/d_w=$2 and ${\xi }_w=$ 0.01.

Fig. 3The ratio of amplitudes Ai/Anci as a function of the coating material shear modulus Gc and the coating material specific damping capacity ξc

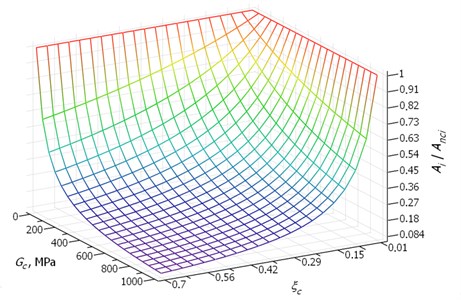
The assumed range of the shear modulus $G_c$ and the specific damping capacity ${\xi }_c$ of the damping coating material includes values of these parameters typical for both industrial rubber and plastics, such as polyurethane, polyethylene of high density or polyamide. Rubber-like materials usually have very good damping properties, but are accompanied by very low shear modulus values. Thus, although they are successfully applied in many different types of dampers [11], it can be seen in Fig. 3 that in the considered case such materials do not provide good results. Materials with good damping properties but higher shear modulus, such as typical polymers [12], provide much higher vibration damping efficiency. It is also visible in Fig. 2 that the relative thickness of the coating plays a major role in damping effectiveness – the increase in the ratio $d_c/d_w$ is accompanied by a slow increase in damping.