Control of elastic-hysteretic characteristics of multilayer all-metal vibration insulators with structural damping

1. Introduction

There are many scientific works where a problem of energy dissipation in the systems with structural damping is studied. One of the most significant works is article of L. Goodman and J. Klamp [1-3]. In this paper, the authors suggested a way of hysteresis calculation, which occurs for bending two-layer console beam. The layers are pressed against each other by constant pressure. The beam rigidly fixed at one end. On the opposite end of the beam the force is applied. For this construction, the mathematic bilinear model of elastic-hysteresis loop was theoretically developed. As the authors note [1, 2, 4-7], the hysteresis is a result of an instant change of the inertia moment of the cross section of the beam at the certain points where the beam is deformed. The changes of the inertia moment of the cross section of the beam are controlled by a distribution of tangential stresses on the height of the beam. The idea of forming the hysteresis, used into the mathematical model [1, 2, 8], is controversial. However, the authors have received accurate data: 1) the dependence of dissipated energy on the amplitude; 2) the presence of extremum on a graph of the dependence of dissipated energy from the contact pressure between the layers.

The similar results were obtained in the research of Kalinin for the multilayer beam compressed by the constant pressure [5, 9, 10]. The authors noted that the slippage of the layers occurs immediately in two-layer beam when a certain force on the end of beam is reached. In the multilayer beam the slip in each of the contact surfaces takes place simultaneously and according to the certain law the slip gradually spreads from surface to surface. It inhibits the growth of the energy dissipation coefficient $\psi$ in the multilayer beam. The higher the energy dissipation coefficient $\psi$, the smaller is the amplitude in the resonance.

In [11-16] an extensive analysis of the opportunities of the different energy dissipation systems with the structural damping (e. g. an all-metal wire rope insulators, shock absorbers made of pressed wire material MR, multilayer dampers with various distribution of pressure between the layers) was carried out on the base of the theory of similarity and dimensionality. It was found that the multilayer structures with an instant slippage and the uniform pressure between the layers have the best damping properties. This finding has led to the development of some effective designs of the damping devices for aviation and engineering industry.

The principle of uniformity of compressive load along the length of the multilayer elastic element is the most simply implemented on the base of wire rope all-metal insulators [5, 17-19]. The elastic element in these vibration insulators consists of one or several wire ropes, tightly wrapped by wire. This elastic element connects two holders of the vibration insulator equipped with fixing bolts.

In [20] the design of a ribbon (instead of wire rope) vibration insulator is described. It is using of the similar idea for aerospace engineering. The uniformity of compression of layers in the package is provided by specially profiled elastic rings, which serve as the supports of the vibration insulator too. Experimental and theoretical study of these designs [20, 23] shown their high efficiency.

Unfortunately, in these designs [20, 21] the maximum value of the energy dissipation coefficient ${\psi }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is realized at the specific amplitude. Therefore, the value of the energy dissipation coefficient is not amenable to control during the process of vibrations. In this regard, the authors of this article had an idea to create the design of all-metal vibration insulators with controlled elastic-hysteretic characteristics. The pressure on the contact surfaces was selected as the parameter for the control of the properties of the all-metal multilayer vibration insulators with structural damping.

Several variants of the all-metal vibration insulators were developed on this principle [21, 24-27]. In one of them [27] (Fig. 1) the package of elastic elements of the square cross-sectional 1 is covered by clamps 2. Within the clamps 2 there are gaskets 3 made of electrostriction material that may change their transverse dimensions under the influence of electric voltage. The voltage is applied to the electrodes of the gaskets 3 from an external source of energy. Gaskets 3 allow changing of the pressure between the layers of the vibration insulator thus changing of the form of the hysteretic loop. Each of the two pairs of the opposite electrostriction elements are associated with independent voltage sources for separate control of the oscillation level in different directions. Voltage sources are controlled by the signals from the sensors of vibrations.

One of the variants of the design of the all-metal vibration insulator with perception spatial load is illustrated on Fig. 2. In the similar way, as in the first design, electrostriction items controlled by electrical voltage can be located under the clamps. Herewith on the mutually perpendicular areas of the vibration insulator the pressure on the layers can be individually controlled, depending on the vibration level in the corresponding direction.

Fig. 1The design of the all-metal vibration insulator with controlled elastic-hysteretic characteristics [27]

Fig. 2The design of the controllable vibration insulator with perception spatial load [3, 27]

2. Materials and methods

It is known that the damping properties of the multilayer vibration insulators have a high level [27-30]. However, it can be improved.

An elastic-damping element is working on bending mainly. Elastic-damping element has a rectangular cross-section (Fig. 3). Zhuravskij D. I. derived an equation which describes the distribution of the shear stresses $\tau$ for a rectangular cross-sectional at bending [3, 31]:

where $P$ is the transverse force in the considered section, N; $b$ is width of a rectangular cross-sectional, m; $H$ is height of a cross-sectional, m; $y$ is the distance from the neutral axis to the corresponding contact surface, m. For multilayer beam $H=hn$, where $n$ is the number of the layers in the multilayer package, $h$ is the height of each layer.

The authors suggested that the dissipation energy coefficient will be maximized if the slippage will occur immediately on all contact surfaces. To achieve this, the height distribution of the friction coefficient $f$ should be the same as the distribution of shear stresses [5, 9]:

where $q$ is the compression pressure of the layers, N/mm².

By substituting Eq. (2) into Eq. (1) we find that on the contact surfaces of a multilayer package (Fig. 1, 2) need to create a pair of friction with the friction coefficient $f$, which obeys the following relationship:

where $P$ is the amplitude of the transverse force at which delaminating of the multilayer package is provided, N. The friction coefficient $f$ reduces roundtrip from the neutral axis (Fig. 3).

When the level of tangential stresses equal to the level of the distributed friction forces ($q_0=f_0$), the simultaneous slippage of all the layers in the multilayer package will happen [25].

At the bending of such an elastic-hysteresis element ($q=const$) the hysteretic loop will be in the form of parallelogram (Fig. 4) with two characteristic stiffness one of which is the initial stiffness (delaminated stiffness), defined by the expression:

And the other is laminated stiffness, defined by the expression:

where $\alpha$ is the angle between the horizontal axis $x$ and the site of the load curve which corresponds to the laminated multilayer beam; $\beta$ is the angle between the horizontal axis $x$ and the site of the load curve which corresponds to the delaminated multilayer beam; $\mu$ is the coefficient that depend on the boundary conditions of the displacement of the movable end of the multilayer beam; $E$ is the modulus of elasticity of material, N/m²; $J=\left(b{h}^3\right)/12$ is the inertia moment of the transverse section of the layer in the multilayer package, m⁴; $l$ is the length of the beam, m.

Fig. 3The cross-section and the graph of distribution of the values of the friction coefficient on the thickness of the multilayer beam

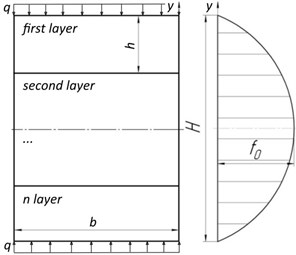
Fig. 4The elastic-hysteretic characteristic of the multilayer all-metal controlled vibration insulator 1

The energy dissipation coefficient $\psi$ is determined as:

where $f_0$ is the maximum friction coefficient of the friction pair on the neutral axis of the multilayer package (Fig. 3). This equation shows that the value of energy dissipation coefficient $\psi$ may be controlled by changing of the value of compression loads $q$. To ensure the permanence of energy dissipation coefficient $\psi ={\psi }_0=const\text{,}$ which does not depend on the force $P$ amplitude, the authors derived the following relationship for the compression loads:

Since the amplitude of the force $P$ acting on the vibration insulator depends on the acceleration of the object of the vibration protection, it is easy to implement dependence Eq. (7) using a simple electronic circuit with an acceleration sensor placed on the object of the vibration protection.

Relationship Eq. (3) of distribution of the friction coefficient on the height of the multilayer package $f\left(x,y\right)$ with the maximum $f_0$ on the neutral axis can be realized with the help of various coverings. Thus, on the basis of the all-metal vibration insulators with structural damping the adjustable systems of the vibration protection can be created.

Let us consider the possibilities of the created model of the adjustable vibration insulator. We define the initial parameters of the system. We have a multilayer steel beam consisting of $n$ layers, height $H=const$. The height of each layer is $h$, the width is $b$, and the length is $l$. We accept the law Eq. (3) of distribution of the friction coefficient on the thickness of the multilayer beam with the maximum of $f_0$ on the neutral axis (Fig. 3). Let suppose that the surface of each layer is treated so that the friction coefficient $f$ on the neutral axis of the multilayer beam is $f_0=$ 0.15. The pressing of the layers of the multilayer beams to each other is provided by the distributed load $q$. The multilayer beam is loaded on its end by the concentrated force $P$.

Taking value $\mu =$ 3 for selected boundary conditions, we denoted the stiffness parameters of hysteresis as:

where $J_P$, $J_0$ are the inertia moments of the cross-section of the laminated and delaminated multilayer beam (Fig. 4).

The laminated moment of inertia is (the layers are deformed independently):

The delaminated moment of inertia is (the layers are deformed together):

Let us determine the force Eq. (12) and the deflection Eq. (13), at which the layers of the beam begin to slip:

Then the maximum force of the separate hysteretic loop with amplitude $A$ is given by:

We find the parameters derived from the hysteretic loop. It is the mean-cyclic stiffness:

And the dissipated cyclic energy $W$, which is equal to the area of the hysteretic loop with arbitrary amplitude $A$:

The energy dissipation coefficient $\psi$ is determined as:

By input of the specific value of the parameters and using Eqs. (3) and (17), we obtained the dependence of the energy dissipation coefficient $\psi$ on the deformation amplitude $A$ and the number of layers of the multilayer beam (Fig. 5):

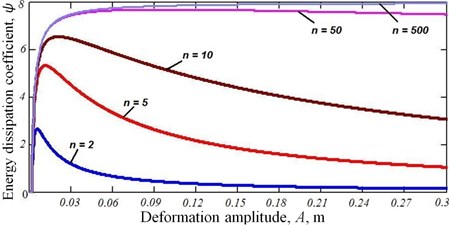
Fig. 5The dependence of the energy dissipation coefficient ψ from the deformation amplitude A. The number of layers in the multilayer beam is fixed. In this, l= 1 m, b= 0.1 m, H=const= 0.1 m, q= 10 MPa, f0= 0.15

Substituting Eqs. (10) and (11) to Eq. (14), with $n\to \infty$ it is easy to find the limit of the function Eq. (17), which turns out to be ${\psi }_{max}=$ 8 at the optimum deformation amplitude:

Dependence Eq. (18) deformation amplitude $A_{optim}$ on the number of layers $n$ of the multilayer beam is the linearly increasing function.

We investigated the dependence of the energy dissipation coefficient $\psi$ on the number of layers $n$ of the multilayer beam with the optimum deformation amplitude $A_{optim}$. We represent the maximum value of the force corresponding to the optimum deformation amplitude $A_{optim}$ as:

And the area of the hysteresis loop for the optimum deformation amplitude $A_{optim}$ as:

Then the energy dissipation coefficient at the optimum deformation amplitude is represented by the expression:

Next, we defined the dependence of the scattered energy on the compressive pressure $q$ at a deformation amplitude $A_{max}=const$ and $n=const\text{.}$ To do this, we substitute in the Eq. (14), the expression (12) of the force of the lamination $P_p$ (Fig. 4). We previously denoted a set of constants as $Z$:

The force $P_0$ at a given value of the compressive pressure $q$ is:

We substitute in the Eq. (16), the Eq. (23). The dependence of the area of the hysteretic loop on the magnitude of the compressive pressure $q$ is:

Next, we defined the maximum compressive pressure $q_{max}$. To obtain the result we equated the left-hand side of the Eq. (24) to zero and solved the resulting quadratic equation for $q$. At the same time, we got rid of the function $if$ in the Eq. (23) of the force $P$. We accept the condition that if $W=$ 0, then the force $P$ is calculated by the delaminated stiffness $C_0$ Eq. (9) because sliding does not occur. Then the maximum value of the compressive pressure $q_{max}$ at which the sliding at a given deformation amplitude $A$ does not occur is defined as:

The optimum pressure $q_{optim}$ is a half of the maximum load $q_{\mathrm{m}\mathrm{a}\mathrm{x}}$ [3, 31]:

We defined the compressive pressure $q$ at the extremum point of function $\psi =f\left(q\right)$, where the energy dissipation coefficient $\psi$ is maximal. To obtain the result, we differentiated the function $\psi =f\left(q\right)$ for $q$ and equated to zero the derivative function. We obtained a quadratic equation, solving which we found:

Next, we defined the dependence of the energy dissipation coefficient $\psi$ on the deformation amplitude $A$ and on the number of layers $n$ of the multilayer beam as:

where:

The study of the dynamic characteristics of the mechanical system is conveniently carried out on the basis of the amplitude-frequency characteristic (AFC). The plot of the AFC presented in the dimensionless form (Fig. 7). It is necessary to determine the dependence of the dynamicity coefficient $\eta$ on the relative frequency of the mechanical system $\nu$. It is known that the dynamicity coefficient $\eta$ depends on the damping coefficient $\gamma$. For a given mechanical system the damping coefficient $\gamma$ depends on the deformation amplitude $A$ [5, 27, 32]. We calculated the average damping coefficient ${\gamma }_{avg}$ as a function of the number of layers $n$ of the multilayer beam to eliminate this dependence within the system. This coefficient does not depend on the deformation amplitude. Therefore, we will use them in further calculations of the dynamics of the mechanical system. The average damping coefficient is defined as [27, 32]:

We obtained an average energy dissipation coefficient ${\psi }_{avg}$ as:

where $S_{\psi }$ is the area under the graph of the dependence of the energy dissipation coefficient $\psi$ on the deformation amplitude $A$.

The functional dependence of the dynamicity coefficient $\eta$ on the dimensionless frequency $\nu$ is given by [5, 33]:

where the dimensionless frequency $\nu$ is defined as:

where the natural circular frequency of the system is:

where $m$ is the mass of the oscillating object.

The values of the energy dissipation coefficient $\psi$ for multilayer beam with the variable friction coefficient $f\left(y\right)$ and the values of $\psi$ for multilayer beam with the equal $f$ [34] on all the contact surfaces are compared. Eskin method allows the calculation of multilyesr beam only with an even number of layers $n$. The number of layers $n$ should be greater than four. Comparison was made at the following parameters: $b=$ 0.1 m, $H=$ 0.1 m, $L=$ 1 m, $f_0=$ 0.15, $q=$ 10⁷ H/m², $E=$ 2.1∙10¹¹ H/m². The comparison was made at similar thickness of the hysteretic loops $W$ for each of the layers $n$. The comparison results are presented in Fig. 6.

3. Results

As a result of our research the following was found.

1. The damping coefficient of the multilayer all-metal vibration insulators (for example, Fig. 1, 2) can be increased. To obtain the result it is necessary to create a pair of friction with the quadratic distribution according to Eq. (3) of the friction coefficient on the contact surfaces of the multilayer beam (Fig. 3).

2. In the multilayer all-metal vibration insulators with the law of the quadratic distribution of the friction coefficients between layers exists optimal deformation amplitude Eq. (18), at which the energy dissipation coefficient $\psi$ is maximal and can be represented by the Eq. (21).

3. The magnitude of compressive pressure $q$ can control the level of the energy dissipation coefficient $\psi$. To ensure the stability of the energy dissipation coefficient $\psi ={\psi }_0=const$ at change the force $P$ (or the deformation amplitude $A$), it is necessary to ensure the law of distribution of the compressive pressure as Eq. (7).

4. The optimum pressure $q$ at which the area of the hysteretic loop is maximal defined from the Eq. (26).

5. The value of the compressive load $q$, required to achieve the maximum value of the coefficient $\psi$, can be got from the Eq. (27).

Fig. 6The dependence of the energy dissipation coefficient ψ on the number of layers n of the multilayer beams

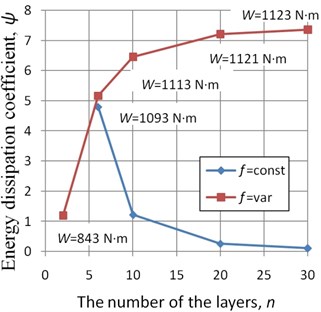
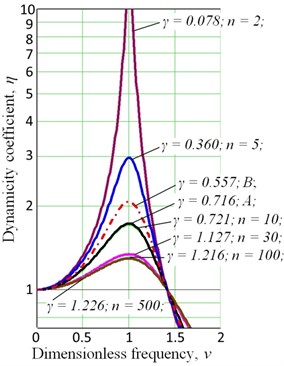
Fig. 7The dependence of dynamicity coefficient η on the dimensionless frequency ν: A – corrugated damper (avg), B – wire pressed materials (avg)

6. The energy dissipation coefficient $\psi$ for multilayer beam with $f=$ variable is larger than for a beam with the uniform $f=const$ when $n=idem$ and $W=idem$ (Fig. 6). For beam with $f=const$ energy dissipation coefficient $\psi$ decreases with increasing number of layers $n$ due to lack of control. For beam with $f=$ variable energy dissipation coefficient $\psi$ increases with $n$ and approaches to the maximum ${\psi }_{max}=$ 8 for systems with structural damping.

7. To evaluate the effectiveness of the vibration isolation systems based on the different elastic-damping elements (e.g. corrugation, pressed wire material MR) we can use dependence of the dynamicity coefficient $\eta$ on the dimensionless frequency $\nu$ (Fig. 7).

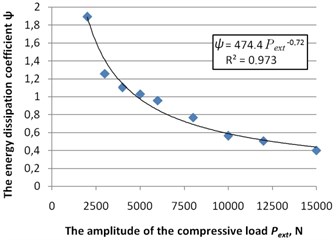
Ability to control stiffness and damping of the multi-layer-metal damper via magnitude compressive load has been proven experimentally [27, 31]. Static tests of the damper were carried out in the mode uniaxial loading. The obtaining of a set of the hysteresis loops when exposed to cyclic compressive force with amplitude on the damper is the basis of experiment $P_{ext}$. The load $P_{ext}$ at the same time compresses the layers and causes a shift between the layers of the damper (sliding between layers). The experimental procedure is described in detail in the source [5, 31]. For the experiment was taken a multilayer steel damper with the following parameters: the number of layers in the package $n=$ 19, the height of the package $H=$ 9.45 mm, the package width $b=$ 33 mm. The experimentally obtained dependencies of the mean-cyclic stiffness C and the energy dissipation coefficient $\psi$ from the load $P_{ext}$ are shown in Fig. 8 and Fig. 9. $R^2$ is the value of reliability of approximation.

It is clearly seen that the mean-cyclic stiffness $C$ increases as the load $P_{ext}$ increases, and the energy dissipation coefficient $\psi$ decreases. This behavior of the parameters is consistent with the calculations given in this paper. In [35, 36] experimentally studied the different coating for plates of frictional dampers with provided constant compressive load (created due to the springs). Researches were carried out at different frequencies and amplitudes. In [37] investigated experimentally the multilayer damper under different loads and different sliding speeds. In [31, 38, 39] was experimentally investigated behavior of the friction coefficient of different pairs of metal strips (of copper, gold, and steel). The effect of the normal load and sliding speed on the coefficient of friction has been investigated.

These studies confirm the possibility of adjusting the hysteretic characteristics of the plate damper by choosing the friction coefficients between the layers and the control of the compressive load.

Fig. 8The dependence of the mean-cyclic stiffness C from the amplitude of the compressive load Pext

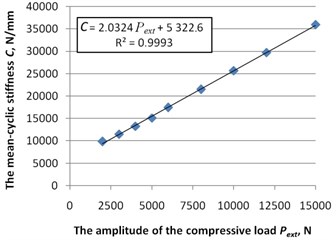
Fig. 9The dependence of the energy dissipation coefficient ψ from the amplitude of the compressive load Pext

4. Conclusions

The analysis of the functional dependence Eq. (17) shown in Fig. 5 shows that the energy dissipation coefficient $\psi$ is practically constant on the operating frequency of the vibration protection system at the number of layers of the elastic-damping element (multilayer all-metal beam) $n>$ 50. Further increase of the number of layers of the multilayer beam gives a slight increase of the coefficient $\psi$. The analysis of the graphs presented in the article, shows that the proposed principles allows to create a fairly simple design that provides an almost constant damping coefficient in a wide range of frequencies and deformation amplitudes of the all-metal vibration insulator. Moreover, at the small deformation amplitudes (in the after resonance region) of the vibration isolation system, the damping coefficient is close to zero, that reduces losses.

It should be noted that we determined the compressive load where the energy dissipation coefficient $\psi$ is maximal Eq. (21) by differentiation the function $\psi =f\left(q\right)$ for $q$ and the equating the derivative to zero Eq. (27).

The analysis of the Eq. (26) shows that for $n=const$, the optimal compressive pressure $q_{optim}$ depends only on the deformation amplitude. And it is a linearly increasing function. This fact allows using the dependence Eq. (26) to design of the vibration isolation systems with the simple parametric control of the elastic-hysteretic characteristics.

The graph of the dynamicity coefficient $\eta$ on the dimensionless frequency $\nu$ (Fig. 7) indicates the advantage of using multilayer all-metal vibration insulators compared with the similar design on the basis of the wire pressed material “metal analogue rubber (MR)” or package of the corrugated tapes at designing parametrically controlled elastic-hysteretic systems. For example, for a beam from 100 layers (each layer is represented by a thin metal plate, the plates have equal thickness) the dynamicity coefficient $\eta$ is 1.127. It corresponds to an increase of the amplitude on only 30 percents at the moment of the resonance. While the pressed wire material MR provides a twofold increase of the amplitude.

Thus, in the course of this research it was found that the multilayer all-metal vibration insulator with simultaneous sliding of the all plates in the package (in which a quadratic distribution of the friction coefficient $f$ along the height of the cross-section and the uniform distribution of the compression $q$ is implemented) provides the energy dissipation coefficient $\psi$ higher than the vibration insulator with a constant friction coefficient between the layers provides. Furthermore, the increasing of the number of layers $n$ leads to an increase of the stability of the energy dissipation coefficient $\psi$ as a function of the deformation amplitude $A$. As a result, even if the package has only a few tens layers, the energy dissipation coefficient is approaching the theoretical limit ${\psi }_{max}=$ 8. Moreover, within the range of operating frequencies the coefficient $\psi$ increases proportionally to the deformation amplitude $A$ (Fig. 5), providing the minimum or zero value of the coefficient $\psi$ for the small amplitudes $A$. It increases the efficiency of the vibration isolation in the range of after resonance frequency (zone of protection from vibration).

Thus, the design, based on the principles proposed in the article, has a linear control law, provides low amplitude at resonance, and effective work in the range of after resonance frequency.