Rheological models of high viscosity silicone fluids

1. Introduction

The viscous type vibration dampers of crankshafts provide the necessary torsional vibration damping effect by elastic and damped coupling of the inertia ring to primary mass (damper housing). When the crankshaft rotates uniformly – without any torsional vibration – the inertia ring in the housing is driven round without any slippage occurring. However, as soon as – even at a very low stage – the vibration amplitudes are superimposed, a relative movement is caused to take place between the housing and the ring, which generates alternating stresses in the silicone layer. The sum of these stresses over the entire gap surface between the inertia ring and the housing results in a damping effect [1]. Older models of the viscous torsional vibration dampers of crankshafts utilized silicone fluids with a quite low kinematic viscosity ($\nu =$0.02-0.06 m² s^-1) and the coupling of the inertia ring to the housing had a character of viscous damping [1]. The progress in the field of polymethylsilicone fluids has enabled the manufacture of silicone fluids with kinematic viscosity $\nu =$ 0.01-0.06 m² s^-1. These fluids show damping and also elastic properties when exposed to oscillating shear stress. Under harmonic oscillating shear stress the viscoelastic properties of the fluid may be described by a complex shear modulus $\stackrel{-}{G}$ which determines the relation between the deformation angle $\stackrel{-}{\gamma }$ and shear stress $\stackrel{-}{\tau }$ [2, 3]:

The real part $G^{\text{'}}$ of the complex modulus determines the storage of elastic energy, the imaginary part $G^{\text{'}\text{'}}$ determines the viscous dissipation. For utilization in the field of silicone dampers of torsional vibrations in IC engines it is necessary to take into consideration the frequency range up to 300 Hz, while both components of the complex shear modulus are frequency- and temperature-dependent. Dynamic viscometers may be used for the experimental determination of behavior of such components [4, 5]. These devices accommodate the fluid between two layers with the defined geometry – one of these (active) is excited and the other (reactive) is flexibly mounted. The measured values are input and output amplitudes, phase shift and the frequency. The components of the complex shear modulus are determined from the measured data and from the solution of motion equations describing the mechanical system of dynamic viscometer.

Parameters of the elastic and damping coupling between the inertia ring and damper housing, see Fig. 1, are determined from the integration of the shear stress to the surfaces of the damper. The so-called “gap coefficient” $\mathrm{\Lambda }$ may be determined from the given geometry of the gaps between the inertia ring and damper housing. The complex stiffness between the inertia ring and damper housing is then calculated as:

The excitation forces and vibrations caused by them are periodic in the crankshaft mechanisms of IC engines. In the dynamic computational models, tens of harmonic components need to be taken into consideration to reach the necessary accuracy while solving in both frequency and time domains. Since the relations Eqs. (1) and (2) are defined only for harmonic vibrations, they cannot be directly used for systems with periodic or general excitation forces. The solution could be a suitable multi-parameter linear viscoelastic model in which the frequency dependence of the real and imaginary part of the complex stiffness would, with a necessary accuracy and within the given frequency range, approximate the behavior described by the Eq. (2) with parameters $G^{\text{'}}$ and $G^{\text{'}\text{'}}$ obtained by the measurement.

Fig. 1Viscous type torsional vibration damper - laser welded technology

2. Rheological models

Two rheological models for high viscosity silicone fluids were created. The first model is the fourth-order Maxwell model, see Fig. 2.

Fig. 2Fourth-order Maxwell model

Fig. 3General model

The complex stiffness of a single serial spring-damper element can be calculated as [6]:

where $k_{ij}$ is the damping coefficient, $c_{ij}$ is the stiffness coefficient, $j$ is the imaginary unit and $\omega$ is the angular frequency. The second model considered in the paper is the general model with no specific structure. The model consists of four massless points. Each point is connected to all the remaining points as well as to the frame by means of single Kelvin units, see Fig. 3. The complex stiffness of the Kelvin elements used in the general model can be described as [6]:

The real and imaginary parts of the complex stiffness $\mathrm{R}\mathrm{e}\left(\omega \right)$ and $\mathrm{I}\mathrm{m}\left(\omega \right)$, respectively, are dependent on the frequency and as well as on the temperature. The complex stiffness of the system can be determined from the solution of the linear set of equations:

where $\mathbf{M}$ is the mass matrix, $\stackrel{-}{\mathbf{C}}$ is the complex stiffness matrix, $\mathbf{x}$ is the displacement vector and p is the vector of forces. In the paper, the system was considered massless ($\mathbf{M}=$ 0). Finally, the resultant complex stiffness is determined as:

where $p_n$ and $x_n$ are the last elements of the vectors $\mathbf{p}={\left(0,\dots ,0,p_n\right)}^T$ and $\mathbf{x}$, respectively.

3. Optimization approach to the determination of parameters

Optimal values of the stiffness $c_{ij}$ and damping $k_{ij}$ coefficients were found with the use of the nonlinear mathematical programming method [7]. The special optimization software GAMS and nonlinear solver CONOPT were applied [8]. The use of the GAMS-CONOPT software has proven significantly better results than in the case of heuristics or the commonly used the least-squares method, see e.g. [9, 10]. The objective function of the implemented optimization model with the constraints can be formulated as:

where $\mathrm{R}{\mathrm{e}}_{exp}$ and $\mathrm{I}{\mathrm{m}}_{exp}$ are the frequency-dependent real and imaginary parts of the complex stiffness, respectively, which were determined experimentally. $\mathrm{R}{\mathrm{e}}_{exp}$ and $\mathrm{I}{\mathrm{m}}_{exp}$ are the simulation values of the frequency-dependent real and imaginary part, respectively, calculated by the optimization model and $N$ is the number of frequencies for which the experimental data were measured. Because the magnitudes of values for the real and imaginary parts of the complex stiffness are of different orders, the relative error in the objective Eq. (7) is utilized. As can be seen from the objective function given in Eq. (7), the goal of the optimization is to find the values of the parameters $c_{ij}$ and $k_{ij}$ which minimize the difference between the experimental and simulated data.

In case of the Maxwell model, the optimization software GAMS is allowed only for the determination of the values for the $c_{ij}$ and $k_{ij}$ coefficients. On the other hand, in case of the general model the GAMS is searching for both the values of parameters as well as for the optimal structure itself. Obviously, the goal is to find the best fit between the experiment and simulation with the model having as few elements as possible. Since the “searching path” and results of the GAMS are very dependent on initial values of variables, the optimization procedure was repeated 1000-times in a loop with the random generation of initial values. Then the best solution from the set of results was identified and considered as the final solution.

4. Results and discussion

The silicone oil with a high viscosity was considered for the investigation. The complex stiffness was measured for the frequency range between 10 Hz and 270 Hz with the step of 20 Hz. The measurements were carried out for two different temperatures of the oil. In particular, the temperatures of 50 °C and 110 °C were considered. The results are presented in Fig. 4, Fig. 5 and Table 1.

Fig. 4The real part of the complex stiffness – comparison between experiment and simulation

Fig. 5The real part of the complex stiffness – comparison between experiment and simulation

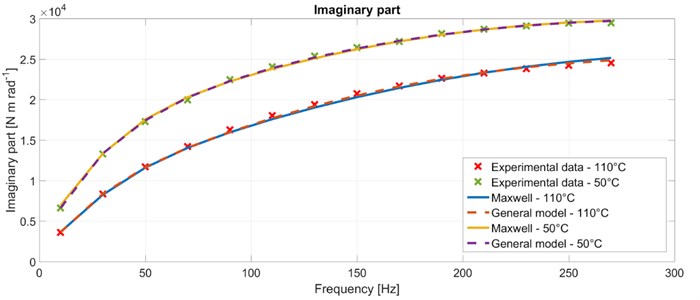
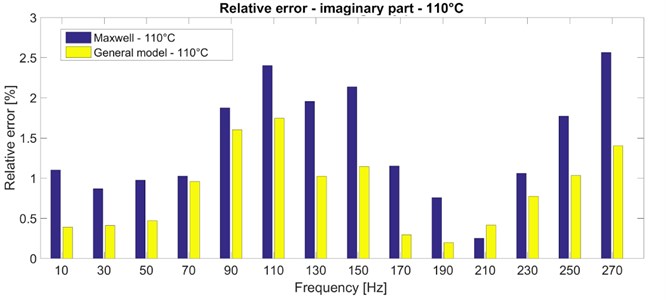
Fig. 4 shows the comparison between the experiment and simulation for the real part of the complex stiffness. As can be seen from the figure, the simulated results provided by both the Maxwell model and the general model are in a very good agreement with the experimentally determined data. This conclusion is valid for both the considered temperatures. Fig. 5 presents the comparison for the imaginary part of the complex stiffness. Similarly, as in the case with the real part, both the Maxwell model and the general model greatly fit the experimental data. In order to investigate the results in more detail, the absolute values of the relative errors between the experimental and simulated data were investigated. As an example, the absolute values of the frequency-dependent relative error for the imaginary part of the complex stiffness and for the temperature of 110 °C are shown in Fig. 6. It can be seen from the figure that the relative error of results determined with the use of the general model is approximately a half of the relative error of results computed by the Maxwell model. As for the resultant objective function, the particular values are presented in Table 1 together with the particular values of the stiffness and damping coefficients $c_{ij}$ and $k_{ij}$, respectively. The Maxwell model has eight parameters in total (four stiffness coefficients and four damping coefficients) from its nature. In case of the general model, the full model consists of 20 parameters in total (10 stiffness coefficients and 10 damping coefficients). However, the best results were achieved with the structures consisting of eight parameters, i.e. the identical number as in case of the Maxwell model, see Table 1.

Note that the objective function is considered as a quality indicator between the experiment and simulation; the lower the value of the objective function the better the approximation. Consider the data related to the temperature of 110 °C. As can be seen from Table 1 the general model enables to provide the approximation with about 20 %-lower value of the objective function (OF) than in case of the Maxwell model. In case of data measured at the temperature of 50 °C, even about 35 %-lower value of the objective function can be attained using the general model instead of the Maxwell model. Since the general model is able to determine both the optimal structure and its parameters, these results make the general model easily applicable to a wide range of different materials used in various damping systems.

Fig. 6Relative error between the experimental and simulated data – imaginary part of the complex stiffness for the temperature of 110 °C

5. Conclusions

The approximation of the rheological behavior for the silicone oil with the high viscosity was investigated with the use of the traditional third-order Maxwell model and with the use of the general rheological model. The Maxwell model with the fixed structure was allowed only for the determination of optimal stiffness and damping parameters while the general model was enabled to find an optimal structure and the corresponding optimal parameters. Although both the models provide a very good approximation, the results have shown that the general model allows for a better approximation and no special care is required to pre-design the structure of the model. These conclusions make the developed general model greatly applicable for various damping materials.