Seismic performance of building structures based on improved viscous damper seismic design

3.1. Building seismic design based on displacement design

In recent years, more and more large-scale buildings have been built. In architectural design and construction, earthquake-resistant design of buildings is the key to construction. Among them, the structural seismic design based on displacement has attracted much attention. Compared with the traditional seismic design based on load-bearing, displacement control pays more attention to the performance and seismic resistance of the building, which is more obvious for the stability and safety of the building structure [15]. In displacement based design, equating multi degree of freedom structures to single degree of freedom is the key to seismic design, mainly because the application of multi degree of freedom equivalence can reduce the difficulty of subsequent calculations and improve the effectiveness of structural design. The principle of displacement seismic design is shown in Fig. 1.

Fig. 1Principle of displacement seismic design

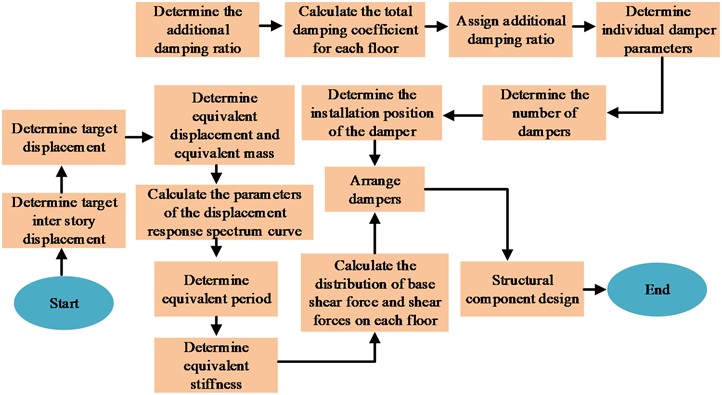
In displacement-based seismic design, it is necessary to determine the performance objectives of the structure, such as considering building stability, durability, and adaptability conditions, etc., and comprehensively determine the performance design requirements based on various factors. In the study, both frequent and rare cases were considered for design. Based on the maximum elastic inter story displacement to floor height ratio of the frame not exceeding 1/550, the inter story displacement angle in frequent cases was set at 1/550. For rare cases, to prevent damage from characteristic earthquakes, the inter story displacement angle was set at 1/100 [16]. In displacement-based design, equating multi-degree-of-freedom structures into single degrees of freedom is the key to seismic design. The equivalent principle of building degrees of freedom is shown in Fig. 2 [17].

Fig. 2Equivalent principle of structural degrees of freedom

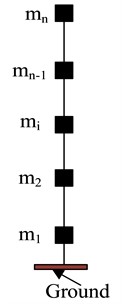
a) Multi degree of freedom system

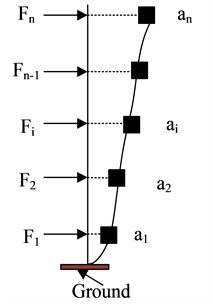
b) Acceleration and inertial force

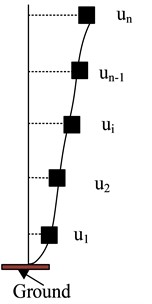
c) Displacement shape

In the design of building structures, the building's multi-degree-of-freedom dynamic system is shown in Eq. (1):

where, $M$ represents the mass matrix, $K$ represents the stiffness matrix, $C$ represents the damping matrix, $\ddot{U}$, $\dot{U}$, and $U$ represent different velocities under three degrees of freedom: multi degree of freedom system, acceleration and inertial force, and displacement shape. ${\ddot{u}}_g\left(t\right)$ representing inertial force. The lateral shift state of the multi-degree-of-freedom system is defined as Eq. (2):

where, $Z\left(t\right)$ represents the normalized coordinates and $\mathrm{\Phi }\left(\xi \right)$ represents the mode matrix. By bringing Eq. (1) and Eq. (2) into the solution, the normalized structural dynamic Eq. can be obtained, such as Eq. (3):

In the equivalent degree of freedom system, set the equivalent displacement as $u_{eff}$, the equivalent acceleration as $a_{eff}$, the equivalent mass as $M_{eff}$, the equivalent base shear force as $V_b$, and the equivalent stiffness as $k_{eff}$, then the $u_i$ equation of multi-degree-of-freedom particle lateral displacement and equivalent displacement $u_{eff}$ is shown in Eq. (4):

where, $a_i$ represents the absolute acceleration of the particle. The seismic force exerted on the multi-degree-of-freedom particle $i$ at this moment is shown in Eq. (5):

where, $m_i$ represents the particle mass. The equivalent base shear force can then be calculated, as shown in Eq. (6):

The equivalent mass can be further obtained from Eq. (5) and Eq. (6), as shown in Eq. (7):

Through the Eq. (7), $i$ the seismic force on the final particle can be obtained, as shown in Eq. (8):

where, $m_j$ and $u_j$ are the single-degree-of-freedom particle mass and equivalent displacement respectively. Under the action of earthquake excitation, the work done by single degree of freedom and multiple degrees of freedom are the same, and there is Eq. (9):

According to Eq. (8) and Eq. (9), the equivalent displacement can be obtained, as shown in Eq. (10):

In addition, in displacement-based seismic design, the equivalent period also needs to be determined $T_{eff}$, which needs to be obtained by constructing a displacement response spectrum. The seismic integral curve is used to construct the displacement response spectrum, and the seismic integral curve is shown in Fig. 3.

Fig. 3Seismic integration curve

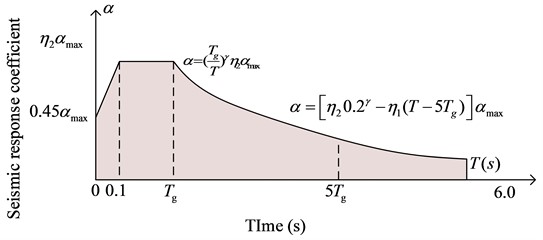
In order to obtain the displacement response spectrum, the dynamic differential equation of the equivalent degree of freedom system is set as ${\ddot{u}}_{\left(t\right)}+2\xi \omega {\dot{u}}_{\left(t\right)}+{\omega }^2{u}_{\left(t\right)}=-{\ddot{u}}_{g\left(t\right)}$, where and $2\xi$ are $\omega$ both damping term parameters, ${\ddot{u}}_{\left(t\right)}$ representing multi-degree-of-freedom acceleration, and $u_{\left(t\right)}$ multi-degree-of-freedom displacement, $u_{\left(t\right)}$ representing the displacement under multi-degree of freedom. Due to the fact that the Duhamet integral is an effective method for solving the response of linear systems under arbitrary external excitation, which improves computational efficiency, the displacement obtained by using the Duhamet integral is shown in Eq. (11) [18]:

where, $T$ represents the seismic response period and $\tau$ represents the interval time, which can be obtained by using the second-order derivative ${\ddot{u}}_{\left(t\right)}$, as shown in Eq. (12):

According to the Eq. (12), the acceleration response spectrum can be obtained, as shown in Eq. (13):

where, ${\alpha }_l$ represents the seismic response coefficient, $S_a$ which is the spectral acceleration, $g$ represents the gravity acceleration, which $S_d$ is the single-degree-of-freedom spectral displacement. The earthquake response period can be obtained from the displacement spectrum, and the period expression is shown in Eq. (14):

In Eq. (14), ${\eta }_2$ represents the damping adjustment coefficient.

3.2. Construction of displacement seismic model based on amplified viscous damping structure

In the displacement-based seismic structural design, in order to reduce the impact of earthquakes on the building structure, appropriate dampers need to be used to reduce the impact of earthquakes on the building. Considering that the research object is concrete steel frame concrete structure buildings, viscous dampers (Viscous Damper, VD) have excellent seismic effects in the seismic resistance of steel frames, concrete frames and other structures [19]. Therefore, viscous dampers are used as the main structure for anti-seismic design. However, traditional viscous dampers have limited energy consumption and poor shock absorption effects in scenarios where structural deformation is small. Therefore, in order to solve the above problems, an Amplified Viscous Damper (Amplified Viscous Damper, AVD) displacement seismic method [20]. The schematic diagram of the enlarged damper device is shown in Fig. 4.

Fig. 4A new type of amplified damper device

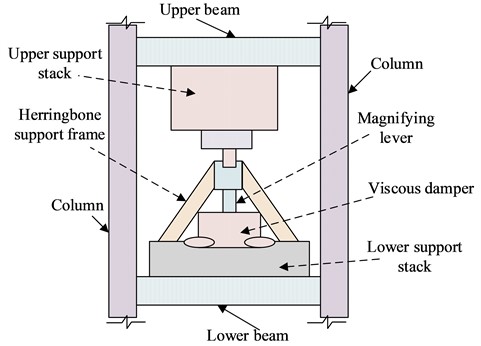
According to the structure of Fig. 4, the device consists of a horizontally placed viscous damper, a vertical amplification lever and a herringbone bracket. In order to analyze the mechanical model of AVD, the AVD mechanical model will be obtained through nonlinear derivation of VD. Suppose the structural velocity is $\dot{u}$, the structural displacement is $u$, and by using the lever device to amplify it $n$ times, the amplified displacement is $u_f=n*u$, and the speed is ${\dot{u}}_f=n*\dot{u}$. Where and are ${\dot{u}}_f$ input $u_f$ into the nonlinear viscous damper model, and the AVD damping force expression is obtained as shown in Eq. (15):

where, $c$ represents the damping coefficient, $\alpha$ represents the damping coefficient. Using the lever amplification effect, the AVD mechanical model is obtained, as shown in Eq. (16):

Expressing $F$ the damping force of ordinary VD, the energy consumption of ordinary VD is expressed as Eq. (17):

The energy consumption of VD after magnification n times is shown in Eq. (18):

Among them, the damping coefficient $c$ is $c_{\delta }$ enlarged $\delta$ to such that ordinary VD and $n$-times enlarged AVD have the same energy consumption and shock absorption ability for the building, then the VD energy consumption at this moment is as follows: Eq. (19):

According to Eq. (19) and Eq. (20), the expression can be obtained $c_{\delta }$, as shown in Eq. (20):

According to the results of Eq. (20), it can be concluded that, under the same other conditions, a VD $c$ magnified $n^{\alpha +1}$ by $n$ times has the same energy consumption and shock absorption effect as an AVD magnified by $n$ times [21]. At the same time, in the construction of the displacement model based on AVD, assuming that the displacement is added to the single free system of the AVD containing the lever amplification type $u$, the acceleration is $\dot{u}$, then the AVD work expression can be obtained as shown in Eq. (21) [22]:

where, $u_0$ represents the displacement amplitude and $\omega$ represents the frequency of external force. Let $dt=(2/\omega )d\theta$, $\omega t=2\theta$, be substituted into Eq. (21) to get the updated one $W_d$, as shown in Eq. (22):

Among them, if intermediate variable parameters are introduced $\lambda$, $\mathrm{\Gamma }$ the function expression is as shown in Eq. (23):

where, $\alpha$ represents the damping index. The damping ratio $\alpha$ has a corresponding relationship with the variable parameters. Refer to the new generation seismic performance method in the United States, as $\lambda$ shown in Table 1 [23].

According to Eq. (22) and Eq. (23), the equivalent damping ratio of the AVD single degree of freedom system is obtained, as shown in Eq. (24):

where, $m$ is the mass of the damper system. Extending the single-degree-of-freedom system to a multi-degree-of-freedom system, the structural elastic strain is obtained, as shown in Eq. (25):

where, ${F_i}^{\text{'}}$ represents the shear force between floors and $i{\mathrm{\Delta }}_i$ represents the displacement between floors. $i$ in a multi-degree-of-freedom system, generally only the first vibration shape is considered, and finally the equivalent damping ratio under the nonlinear AVD multi-degree-of-freedom system can be obtained, as shown in Eq. (26) [24]:

where, $A$ represents the maximum displacement of the top floor of the building, represents the ${\varphi }_{rj}$ regularized relative displacement of $c_j$ the $j$th damper under the first-order vibration shape, $j$ represents the coefficient of the $j$th damper, represents $m_i$ the mass of the th system, ${\varphi }_i$ represents the regularized displacement of the top-level displacement, ${\xi }_0$ represents the system Inherent damping ratio.

4.1. Experimental analysis of frequent earthquakes

In order to verify the proposed displacement seismic design performance, a 6-story reinforced frame concrete building will be selected for seismic experimental analysis, and the two seismic design objectives of frequent and rare occurrences will be analyzed. The experiment uses a 6-story cast-in-place reinforced concrete structure designed by the PKPM platform of the China Institute of Building Research as an experiment. At the same time, combined with the principle of equivalent structural degrees of freedom, different directional degrees of freedom loads are converted into equivalent vertical loads for convenient experimental calculations. The specific parameters of the structure are shown in Table 2.

At the same time, there are two types of structural design target damper deployment schemes for the PKPM platform: frequent and rare. The arrangement of frequent and rare dampers is shown in Table 3.

In the analysis of frequent earthquakes, refer to Table 3 for experimental parameters. According to the demand, two natural waves, Ken County (Ken County, KC) and Humbolt bay (Humbolt bay, HB) in 1952, were selected as experiments. In the analysis of frequent earthquakes, the peak acceleration is 110 cm/s². The comparison of the structural vertex displacement is shown in Fig. 5.

Fig. 5Comparison of displacement of structural vertices

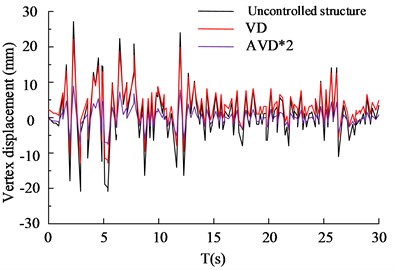
a) HB wave $X$-axis vertex displacement

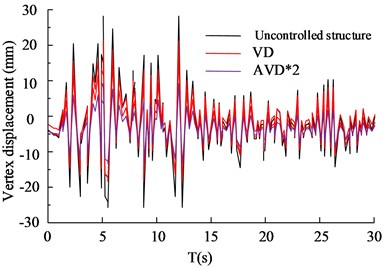
b) HB wave $Y$-axis vertex displacement

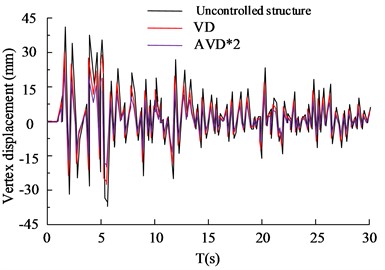
c) KC wave $X$-axis vertex displacement

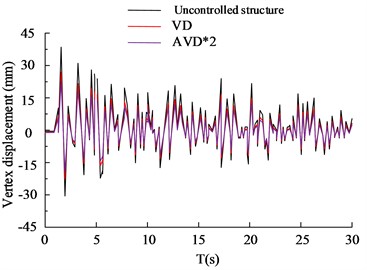
d) KC wave $Y$-axis vertex displacement

Fig. 5(a) to 5(b) show the vertex displacement in the $X$ and $Y$ directions of the HB wave, respectively. From the data results, it can be seen that in frequent earthquake scenarios, VD structures have significant advantages in seismic performance compared to AVD*2 structures without control. The VD structure has a 27.65 % increase in seismic reduction compared to uncontrolled structures, while the AVD*2 structure has a 35.65 % increase in seismic reduction compared to uncontrolled structures. Fig. 5(c) and 5(d) show the displacement of KC wave vertices in the $X$ and $Y$ directions, respectively. According to the data results, VD and AVD*2 with structural design have significantly smaller displacement in the $X$ and $Y$ directions compared to uncontrolled structures. Compared with AVD * 2, the uncontrolled structure of VD has an increase of 24.35 % and 32.35 % in shock absorption rate, respectively. It can be seen that VD and AVD*2 optimize the displacement variation of the building structure in the $X$ and $Y$ directions, reduce the force by improving the viscous damper, shorten the movement of the $X$ and $Y$ axes, and significantly improve the safety of the building structure. The comparison of shear forces on structural floors is shown in Fig. 6.

Fig. 6(a) to Fig. 6(b) are the HB wave $X$- and $Y$-direction shear force diagrams respectively. According to the curves in the figure, there are obvious differences in the seismic effects of the three types of seismic structure designs between floors. Among them, the AVD*2 structure with the best performance has the $X$-direction floor shear force controlled at 2186 KN on the first floor, while the VD structure is controlled at 2556 KN, and the Uncontrolled structure shear force is 2498 KN. In the $Y$-direction floor shear analysis, there are big differences between the three structures. The maximum floor shear force is still on the first floor. The maximum shear forces of no structure, VD and AVD*2 are 1956 KN, 1465 KN and 1265 KN respectively. Fig. 6(c) to Fig. 6(d) are the KC wave $X$- and $Y$-direction shear force diagrams respectively. It can be seen from the comparison of the curves that in the comparison of shear forces between floors in the Comparing the shear force, the AVD*2 structure with the smallest shear force control has a shear force value of 1503 KN, followed by VD with a shear force value of 1635 KN. The worst performance is the uncontrolled structure with a shear force value of 2623 KN. It can be seen that adopting structural design can significantly reduce the impact of seismic forces, mainly due to more effective seismic structural design, which offsets the forces from multiple directions of earthquakes. However, uncontrolled structures cannot counteract the forces, causing the structure to be affected by more forces and significantly reducing safety. Fig. 7 shows the displacement comparison results between structural floors.

Fig. 6Comparison of shear forces on structural floors

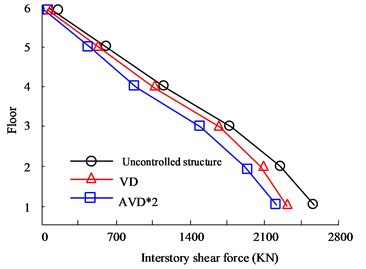
a) HB wave $X$-direction floor shear force

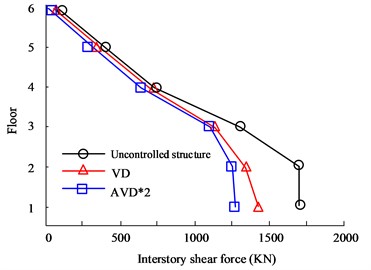
b) HB wave $Y$-direction floor shear force

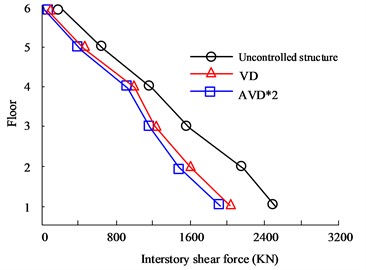
c) KC wave $X$-direction floor shear force

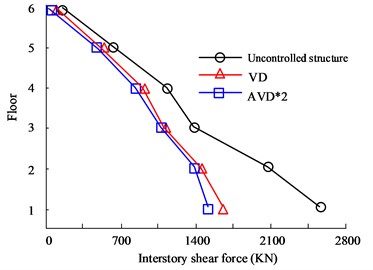
d) KC wave $Y$-direction floor shear force

Fig. 7(a) to Fig. 7(b) are the $X$- and $Y$-direction displacement diagrams of the HB wave respectively. Judging from the data curve, as the number of floors continues to increase, the displacement between floors will continue to expand. When the floor reaches 6 floors, the maximum inter-floor displacement value will be obtained. Therefore, when comparing the inter-story displacement values of different structural designs on the 6th floor, in the comparison of $X$-direction displacement values, the largest displacement value is the uncontrolled structure, with a maximum value of 31.95 mm, followed by the VD structure, with a maximum value of 21.05 mm. The smallest inter-layer displacement is the AVD*2 structure, with a maximum value of 18.35 mm. In the comparison of $Y$-direction floor displacement values, the maximum displacement values of no structural design, VD, and AVD*2 on the 6th floor are 19.36 mm, 20.35 mm, and 10.68 mm respectively. It can be seen from the data structure that structural design is obviously better in seismic displacement control than uncontrolled structure. Fig. 7(c) to Fig. 7(d) are the KC wave $X$- and $Y$-direction displacement diagrams respectively. The test results are consistent with the HB test results. The AVD*2 structural design still has better seismic resistance in the $X$ and $Y$ directions. For example, in the $X$-direction floor displacement comparison, the maximum inter-story displacement value of the Uncontrolled structure is 43.35 mm, while the AVD*2. The maximum inter-story displacement value is 19.05 mm. It can be seen that AVD*2 structural design can significantly reduce the displacement effect of earthquakes on floors compared with no-structure design, and minimize earthquake hazards.

Fig. 7Comparison of displacement between structural floors

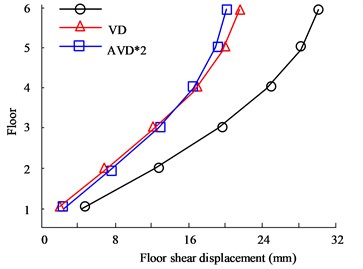
a) HB wave $X$-direction floor displacement

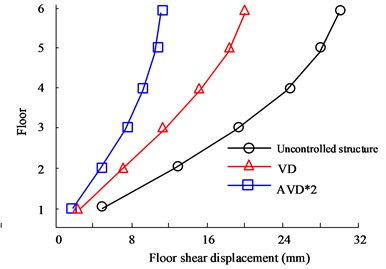
b) HB wave $Y$-direction floor displacement

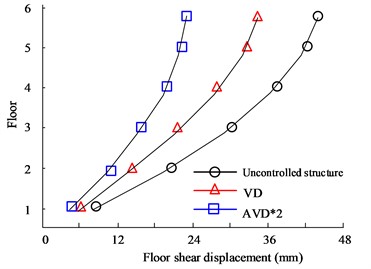
c) KC wave $X$-direction floor displacement

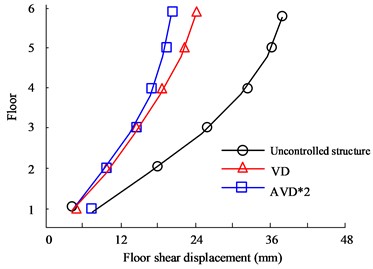
d) KC wave $Y$-direction floor displacement

4.2. Analysis of rare earthquakes

The HB wave and KC wave in the experiment were still selected for the experiment, but the peak acceleration was increased to 510 cm/s² to carry out 8-degree (0.3 g) rare earthquake experimental analysis. The remaining parameters are set according to the parameters of rare regions. The structural vertex displacement comparison is shown in Fig. 8.

Fig. 8(a) to Fig. 8(b) are the HB wave $X$- and $Y$-direction structural vertex displacement diagrams respectively. Judging from the data curve in the figure, the AVD*2 and AVD*3 structural designs can control the $X$-direction vertex displacement within the range of 50 mm, while VD can control the $X$-direction vertex displacement within the range of 100 mm. The maximum $X$-direction vertex displacement value of the structure-free design is 112 mm. In the comparison of the $Y$-direction structural apex displacement, the AVD*3 structural design performed best, followed by AVD*2, VD and no-structure design. Among them, the maximum displacement of the AVD*3 structure was controlled within the range of 30 mm, compared with 88 mm of the no-structure design. There is a significant improvement. Fig. 8(c) to Fig. 8(d) are the KC wave $X$ and $Y$ structure vertex displacement diagrams respectively. The test results are basically consistent with the HB wave test results. The AVD*3 structural design has better overall seismic resistance than the other two structural designs. The shock absorption rate of AVD*3 structural design is increased by 25.65 % compared to the structure-free design, the shock absorption rate of AVD*2 is increased by 21.56 % compared to the structure-free design, and the shock absorption rate of VD is increased by 12.35 % compared to the structure-free design. The comparison of structural floor shear forces is shown in Fig. 9.

Fig. 8Comparison of displacement of structural vertices

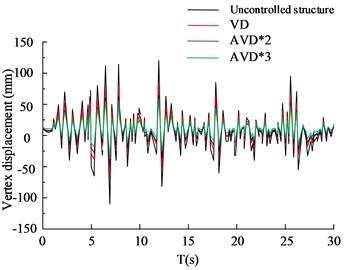
a) HB wave $X$-axis vertex displacement

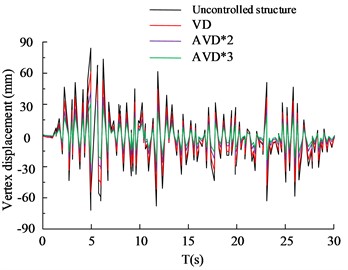
b) HB wave $Y$-axis vertex displacement

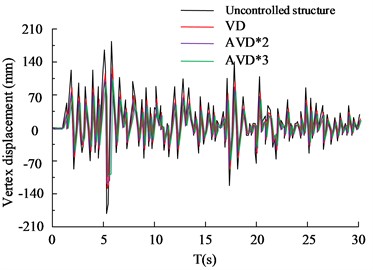
c) KC wave $X$-axis vertex displacement

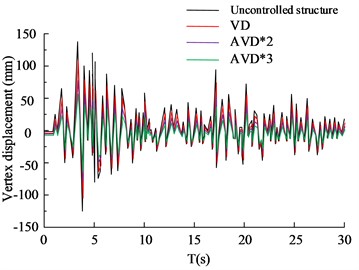
d) KC wave $Y$-axis vertex displacement

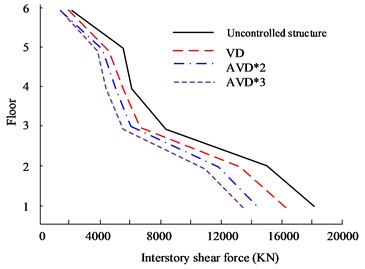
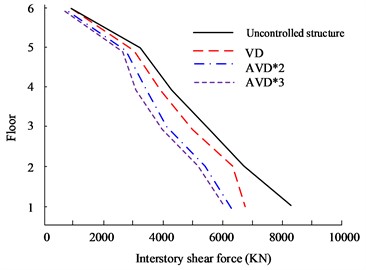
Fig. 9Comparison of shear forces on structural floors

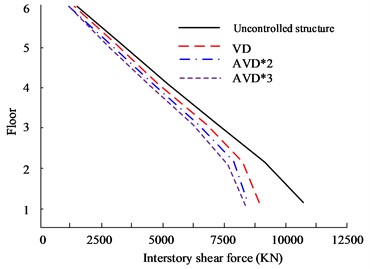
a) HB wave $X$-direction floor shear force

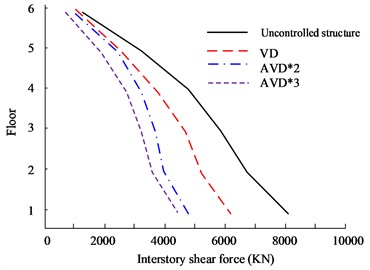
b) HB wave $Y$-direction floor shear force

c) KC wave $X$-direction floor shear force

d) KC wave $Y$-direction floor shear force

Fig. 9(a) to Fig. 9(b) are the HB wave $X$- and $Y$-direction shear force diagrams respectively. In rare earthquakes, the lower the floor, the more obvious the inter-floor shear force will be. Therefore, the first layer was selected for experimental analysis. In the shear force analysis between floors in the 8699 KN, while VD is 8865 KN. At the same time, in the $Y$-direction floor shear comparison, the AVD*3 structure still has the smallest inter-story shear value, which is 4486 KN, while the Uncontrolled structure is 8006 KN. Fig. 9(c) to Fig. 9(d) are the KC wave $X$- and $Y$-direction shear force diagrams respectively. AVD*2 and AVD*3 still have excellent shear force control effects. In the $Y$-direction floor shear force analysis, the maximum interstory shear force of the AVD*3 structure on the first floor is 6105 KN, while the maximum interstory shear force of AVD*2 is 6105 KN. The shear force is 6186 KN. Fig. 10 shows the comparison results of displacement between structural floors.

Fig. 10Comparison of displacement between structural floors

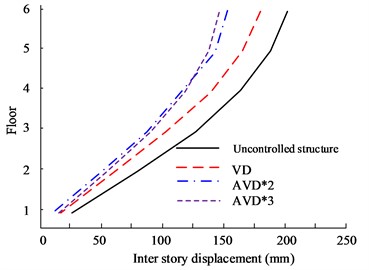
a) HB wave $X$-direction floor displacement

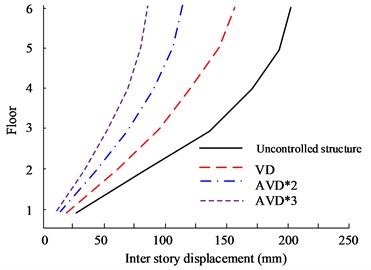
b) HB wave $Y$-direction floor displacement

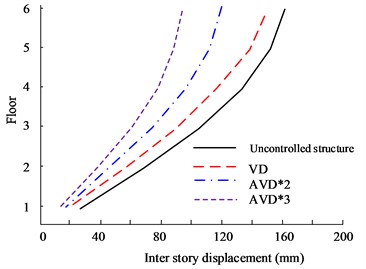
c) KC wave $X$-direction floor displacement

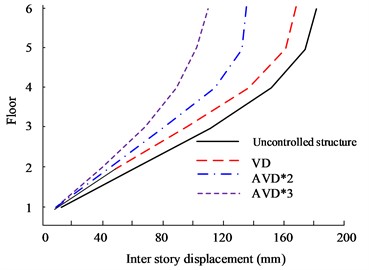
d) KC wave $Y$-direction floor displacement

Fig. 10(a) to Fig. 10(b) are the $X$- and $Y$-direction interlayer displacement diagrams of HB wave respectively. According to the data, the maximum inter-story displacement value appears on the highest floor, and the 6th floor has the maximum displacement value. From a comprehensive comparison, it can be seen that AVD*3 and AVD*2 have the smallest inter-layer displacement values in the $X$ and $Y$ directions. In the comparison of X-direction inter-story displacement values, the maximum inter-story displacement values of AVD*3 and AVD*2 are 162 mm and 169 mm respectively, while the maximum inter-story displacement value of the Uncontrolled structure is 212 mm. Fig. 10(c) to Fig. 10(d) are the KC wave $X$- and $Y$-direction interlayer displacement diagrams respectively. The test results are consistent with the HB wave test results. AVD*3 still has better inter-layer displacement control effect.