A novel method for detecting bearing defects based on EMD and fractal dimension

2.1. Empirical mode decomposition

Hilbert Huang Transform (HHT) is a new signal processing method which developed by Huang et al. [14, 15]. It contains two parts: EMD and Hilbert spectrum analysis method. As the kernel of HHT, EMD has been developed and widely used in fault diagnosis of rotating machinery recently. Using EMD, the complex signal can be decomposed into a set of complete, simple and almost orthogonal components named intrinsic mode functions (IMF). The IMFs represent the natural oscillatory mode embedded in the signal and work as the basis functions, which are determined by the signal itself. And the IMFs should satisfy the following two conditions: (1) In the whole data set, the number of extreme and the number of zero-crossings must either be equal or differ at most by one; and (2) At any point, the mean value of the envelope defined by local maxima and minima must be zero. Namely, local signal is symmetrical about the time axis.

EMD is developed based on the assumption that any signal consists of many different IMFs. The procedures of decomposing a given signal $x\left(t\right)$ to different IMFs can be categorized into the following steps. First, identify all the local extreme from the given signal and then connect them with a cubic spline line as the upper envelope $l_{max}\left(t\right)$. Second, repeat the first step for the local minima to produce the lower envelope $l_{min}\left(t\right)$. The upper and lower envelopes should cover the entire signal between them. Third, compute their mean as $m_1\left(t\right)$ and the difference between the signal $x\left(t\right)$ and $m_1\left(t\right)$ is $h_1\left(t\right)$:

Ideally, after the sifting operation of Eq. (1), $h_1\left(t\right)$ should be the first IMF. The construction of $h_1\left(t\right)$ described above seems to satisfy all the requirements of IMF. However, during the practical process, the theoretical upper envelope $l_{max}\left(t\right)$ and lower envelope $l_{min}\left(t\right)$ are very difficult to calculate. In addition, any little inflection points of the monotonous signal can be transformed to new extrema. And these new extremas should be contained by the next sifting operation. To solve this dilemma, Huang et al. repeated the sifting process of Eq. (1) as many times as required to reduce the extracted signal to an IMF. Therefore, the fourth step is to repeat the sifting process by treating $h_1\left(t\right)$ as the original signal as follows:

The sifting process will be repeated $k$ times until $h_{1k}\left(t\right)$ becomes a true IMF, that is:

Then, make $c_1\left(t\right)=h_{1k}\left(t\right)$, and can be seemed as the first IMF. Remove $c_1\left(t\right)$ from the signal $x\left(t\right)$, namely:

And generate the residue signal $r_1\left(t\right)$. Treating $r_1\left(t\right)$ as a new original signal and repeating the same sifting process above, the second IMF can be got. Similarly, a series of IMFs ($c_i\left(t\right)$ ($i=$1, 2,…, $n$)) can be obtained until the final residue $r_n\left(t\right)$ is monotonous. Then the original signal $x\left(t\right)$ can be reconstructed as:

The IMFs $c_1$, $c_2$,…, $c_n$ represent different frequency bands ranging from high to low. The frequency components contained in each frequency band are different and they change with the variation of the original signal $x\left(t\right)$, and $r_n\left(t\right)$ represents the central tendency of signal $x\left(t\right)$.

2.2. Fractal dimension

The vibration signals of mechanical equipment always have non-linear. Fractal theory is an effective means to deal with this dilemma. As an essential parameter in fractal theory, fractal dimension (FD) has been widely used in many areas of science, including the capability of quantitative measurement for fractal characteristics of nonlinear systems and the ability of space-filling capacity measurement for signals. In mechanical fault diagnosis, the influences of nonlinear factors for mechanical vibration signals are different under diverse fault status. Fractal dimension describes the fault features of mechanical system and recognizes the fault status of mechanical device effectively. In the field of vibration signal processing, fractal box dimension and correlation dimension are two parameters that usually used by researchers. However, the calculate process of correlation dimension is very complicated. So this paper mainly studies the fractal box dimension.

Assume that $Y\subset R^n$, $Y\ne \mathrm{\Phi }$, if there are $N\left(\epsilon \right)$ hypercube can cover $Y$, then:

Eq. (6) is the definition of fractal box dimension.

2.3. The bearing defects detecting method

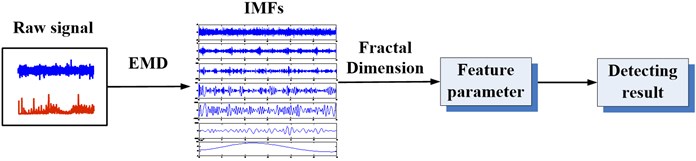
The flow chart of the method based on EMD and FD which proposed in this paper is shown in Fig. 1. It consists of the following procedural steps. (1) Obtain several IMFs by EMD decomposition. (2) Compute out the FD of each IMF. (3) Gain the detecting result.

Fig. 1Flowchart of the proposed method

3.1. Experimental setup and data acquisition

A mechanical test bed in the RCM laboratory of Mechanical Engineering College is used in this research to validate the effectiveness of the proposed method in this paper. The gearbox is driven by a 4 KW three phase asynchronous drive motor. In addition, the speed and torque sensors are used to acquire the speed and torque information, a magnetic powder brake is utilized to provide load. These components are connected by couplings, as shown in Fig. 2. The sampling frequency of this experimental system is 20 kHz.

Bearings are defected after experiment. This paper chooses four states to analyzing. The four states are normal state, ball defect, inner face defect and outer face defect, as Fig. 3 shows.

Fig. 2The test rig

Fig. 3The states of bearings

3.2. Results analysis and discussion

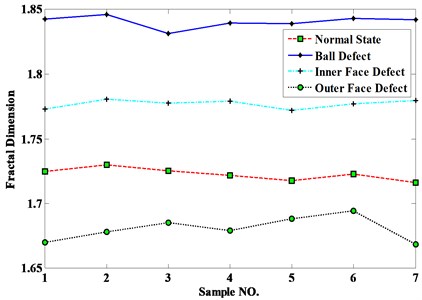
The vibration signal acquired from the test rig is utilized to analyzing according to the method proposed in Section 2.3. Fig. 4 is the detecting results using the method proposed in this paper. It can be seen from the figure that the classification result is very obvious.

Fig. 4Detection results using the proposed method

In order to validate the necessity of EMD, this paper analyzes the data but without processed by EMD and the results can be seen in Fig. 5. The detecting results of normal state, inner face defect and outer face defect are confused. So, the necessity of EMD can be validated.

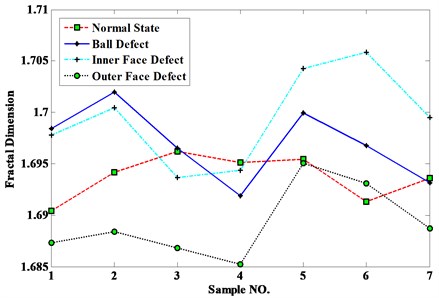
In order to validate the effectiveness of method proposed in this paper, a method based on wavelet and fractal dimension is utilized. It can be seen from Fig. 6 that all of the four states are confused seriously. So, the effectiveness of the method can be validated.

Fig. 5Detection results without EMD

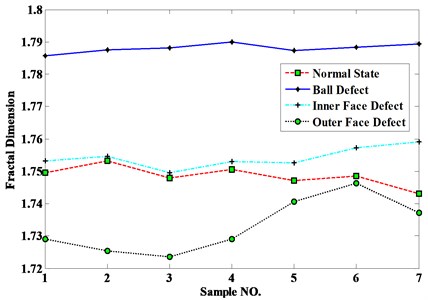
Fig. 6Detection results using wavelet and FD