Method for direct identification of optimum modal values of dynamical systems

Nistyuk, A. I.; Danilov, M. V.; Sivtsev, N. S.; Kugultinov, S. D.

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

Method for direct identification of optimum modal values of dynamical systems

A. I. Nistyuk¹

M. V. Danilov²

N. S. Sivtsev³

S. D. Kugultinov⁴

^{1, 2, 3, 4}Kalashnikov Izhevsk State Technical University, Izhevsk, Russia

Corresponding Author:

A. I. Nistyuk

Cite the article Download PDF

Downloads 1285

Abstract

The synthesis method of a dynamic system by successive solutions of two systems of algebraic equations, variables that are characteristic polynomial coefficients and mechanical parameters of the system.

1. Determination of modal coefficients

Under the synthesis of parameters of the tape-transport mechanism (Fig. 1) [1, 4] it is understood as directed calculation of structural elements having one of the ultimate goals of eliminating the resonance phenomena in the tape transport mechanism and finding the optimal parameter values between the individual units. This goal will be achieved in compliance with the conditions:

1

\underset{j}{\forall} \underset{r}{\forall} ω_{r} \notin (α_{j} β_{j}), 1 \leq j \leq m, 1 \leq r \leq n

Fig. 1Model simplified kinematic scheme tape-transport mechanism. m, k – mass and stiffness of components

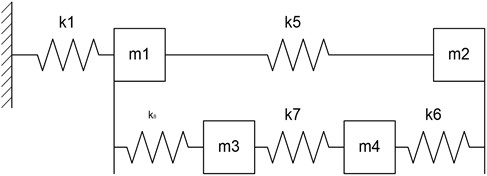
For the preparation of the differential equations describing the dynamic model of the tape-transport mechanism, we use the method of sections. The equations of motion for the dynamic model without exposure to the external disturbances are as follows:

- m_{1} {\ddot{x}}_{1} = k_{1} x_{1} + k_{5} x_{1} - k_{5} x_{2} + k_{8} x_{1} - k_{8} x_{3}, - m_{2} {\ddot{x}}_{2} = k_{5} x_{2} - k_{5} x_{1} + k_{6} x_{2} - k_{6} x_{4},

- m_{3} {\ddot{x}}_{3} = k_{8} x_{3} - k_{8} x_{1} + k_{7} x_{3} - k_{7} x_{4}, - m_{4} {\ddot{x}}_{4} = k_{6} x_{4} - k_{6} x_{2} + k_{7} x_{4} - k_{7} x_{3} .

Synthesized characteristic equation of the system:

2

a_{4} p^{4} + a_{3} p^{3} + a_{2} p^{2} + a_{1} p + a_{0} = 0,

In this equation, coefficients $a_{n}$ depend on system parameters $m_{i}$ and $k_{i}$ . In particular $a_{4} = m_{1} m_{2} m_{3} m_{4}$ . Calculation of other factors associated with cumbersome calculation formulas, so we propose a method of calculating the equation formalization coefficients (2).

In this case, the coefficients (2) can be written as follows:

3

a_{4} = m_{1} m_{2} m_{3} m_{4},

a_{3} = - (k_{1} m_{1} m_{2} m_{3} + m_{1} m_{2} m_{4} k_{7} + m_{1} m_{2} m_{4} k_{8} + m_{1} m_{2} m_{3} k_{6} +

+ m_{1} m_{2} m_{3} k_{7} + m_{1} m_{3} m_{4} k_{5} + m_{1} m_{3} m_{4} k_{6} + m_{2} m_{3} m_{4} k_{5} + m_{2} m_{3} m_{4} k_{8}),

a_{2} = k_{1} m_{2} m_{4} k_{7} + k_{1} m_{2} m_{4} k_{8} + k_{1} m_{2} m_{3} k_{6} + m_{1} m_{2} k_{6} k_{7} + m_{1} m_{2} k_{6} k_{8} + k_{1} m_{2} m_{3} k_{7}

+ m_{1} m_{2} k_{7} k_{8} + k_{1} m_{3} m_{4} k_{5} + m_{1} m_{4} k_{5} k_{7} + m_{1} m_{4} k_{5} k_{8} + m_{1} m_{3} k_{5} k_{6} + m_{1} m_{3} k_{5} k_{7}

+ k_{1} m_{3} m_{4} k_{6} + m_{1} m_{4} k_{6} k_{7} + m_{1} m_{4} k_{6} k_{8} + m_{1} m_{3} k_{6} k_{7} + m_{2} m_{4} k_{5} k_{7} + m_{2} m_{4} k_{5} k_{8}

+ m_{2} m_{3} k_{5} k_{6} + m_{2} m_{3} k_{5} k_{7} + m_{3} m_{4} k_{5} k_{6} + m_{2} m_{4} k_{7} k_{8} + m_{2} m_{3} k_{6} k_{8} + m_{2} m_{3} k_{7} k_{8}

+ m_{3} m_{4} k_{5} k_{8} + m_{3} m_{4} k_{6} k_{8},

a_{1} = - (k_{1} m_{2} k_{6} k_{7} + k_{1} m_{2} k_{6} k_{8} + k_{1} m_{2} k_{7} k_{8} + k_{1} m_{4} k_{5} k_{7} + k_{1} m_{4} k_{5} k_{8} + k_{1} m_{3} k_{5} k_{6}

+ m_{1} k_{5} k_{6} k_{7} + m_{1} k_{5} k_{6} k_{8} + k_{1} m_{3} k_{5} k_{7} + m_{1} k_{5} k_{7} k_{8} + k_{1} m_{4} k_{6} k_{7} + k_{1} m_{4} k_{6} k_{8}

+ k_{1} m_{3} k_{6} k_{7} + m_{1} k_{6} k_{7} k_{8} + m_{2} k_{5} k_{6} k_{7} + m_{2} k_{5} k_{6} k_{8} + m_{2} k_{5} k_{7} k_{8} + m_{4} k_{5} k_{6} k_{7}

+ m_{4} k_{5} k_{6} k_{8} + m_{3} k_{5} k_{6} k_{7} + m_{2} k_{6} k_{7} k_{8} + m_{4} k_{5} k_{7} k_{8} + m_{2} m_{4} k_{7} k_{8} + m_{2} m_{3} k_{6} k_{8}

+ m_{2} m_{3} k_{7} k_{8} + m_{3} m_{4} k_{5} k_{8} + m_{3} m_{4} k_{6} k_{8},

a_{0} = k_{1} k_{5} k_{6} k_{7} + k_{1} k_{5} k_{6} k_{8} + k_{1} k_{5} k_{7} k_{8} + k_{1} k_{6} k_{7} k_{8} .

It is assumed that the boundaries of the resonance-hazardous areas ( $α_{j}$ , $β_{j}$ ) are known. The selection of the absolute values of natural frequencies $ω_{r}$ , $r = 1,2, \dots, n$ , in compliance with the conditions (1), where $n$ – number of degrees of freedom of the synthesized system, is possible then. These frequencies are the roots of the Equation (2), whose coefficients (3) depend on the parameters of links of the tape transport mechanism, where $k_{1}, . ., k_{8}$ are rigidity sections of transported tape, $m_{1}, \dots, m_{4}$ – mass inertial elements of the mechanism. Therefore, determining the values of the coefficients of the Equation (2) satisfy its given roots $ω_{r}$ , $r = 1,2, \dots, n$ , you can get the numerical values of the synthesized system parameters, the optimum in terms of the lack of resonance phenomena is available in the tape transport mechanism [3].

It is provided to determine the coefficients of (2) satisfying given roots in two ways.

The first one is the expansion of the characteristic Equation (2) into prime factors. So we asked a priori $n$ its roots, then in general form it will look like as follows:

4

(1 - \frac{ω^{2}}{ω_{1}^{2}}) (1 - \frac{ω^{2}}{ω_{2}^{2}}) . . . (1 - \frac{ω^{2}}{ω_{n}^{2}}) = \prod_{r = 1}^{n} (1 - \frac{ω^{2}}{ω_{r}^{2}}) = 0 .

Introducing the substitution $p = ω^{2}$ and opening (4), we obtain:

5

\sum_{r = 0}^{n} C_{r} p^{2} = 0 .

To find the coefficients $C_{r}$ and to define the function $Φ (y)$ :

6

Φ (y) = \sum_{i = 1}^{r} y_{i},

where $y = (J_{1}, J_{2}, . . ., J_{r})$ is the binary number $J$ . Given (6) $C_{r}$ values of the coefficients of (5) are calculated using the following formula:

7

C_{r} = {(- 1)}^{r} \sum_{J : Φ (y) = n - r}^{2^{r}} \prod_{i = 1}^{n} f (J_{i}), where f (J_{i}) = \{\begin{matrix} 1, & J_{i} = 0, \\ ω_{i}^{2}, & J_{i} = 1 . \end{matrix}

In view of the Equation (7), we can write a special case of the Equation (5) in the form:

8

p^{4} + c_{3} p^{3} + c_{2} p^{2} + c_{1} p_{1} + c_{0} = 0 .

Multiply (8) by a constant factor $k$ , we obtain:

9

k p^{4} + k c_{3} p^{3} + k c_{2} p^{2} k c_{1} p_{1} + k c_{0} = 0 .

Fig. 2General view of logarithmic frequency response for conservative systems

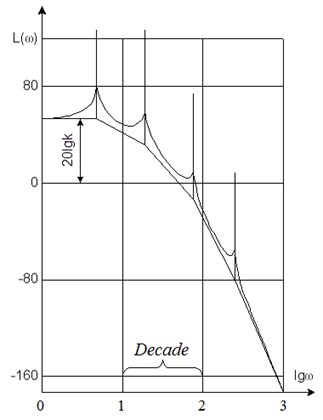
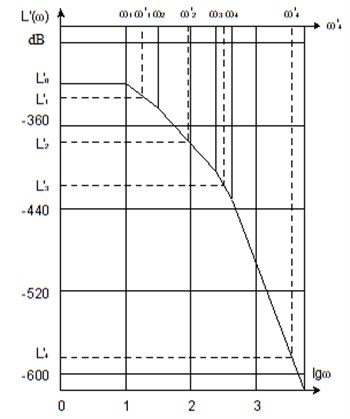
Fig. 3Example of desired asymptotic logarithmic frequency response

Comparing (2) and (9), consisting of the following system of equations:

10

a_{0} = k c_{0}, a_{1} = k c_{1}, a_{2} = k c_{2}, a_{3} = k c_{3}, a_{4} = k .

The coefficient of the term of the characteristic Equation (2) with a degree $2 n$ is always equal to the product of the masses, in the system, i.e. $k = m_{1} m_{2} m_{3} m_{4}$ . By setting a priori this factor taking into account the real possibilities of change limit of the mass inertia of the system units all the coefficients of the Equation (2) can be determined.

Another way to determine the coefficients of the Equation (2) is to use logarithmic amplitude-frequency characteristics, namely its asymptotic approximation. Construction of the last being almost non-computational work, which greatly simplifies the process of determining the parameters of parts of the tape transport mechanism, and thus by constructing the desired asymptotic logarithmic frequency response we can define the parameters of the transport mechanism of tape units. The logarithmic frequency response is based on the following expression:

11

L (ω) = 20 l g |W (p)| = 20 l g \frac{1}{|D (p)|},

where $D (p)$ is the characteristic polynomial of Equation (2) whose roots are the values of $ω_{r}$ . General view of logarithmic amplitude frequency characterized for a conservative system [2] is shown in Fig. 2. The asymptotic logarithmic frequency response is shown here. The latter analysis shows that it is a piecewise linear function with n points of the first kind discontinuity. By the property of logarithmic frequency response of a conservative system the slope after each root of the characteristic equation is increased by 40 dB per decade.

Thus, the construction of the desired asymptotic logarithmic frequency response is provided to conduct a polygonal curve with break points for the values of the polynomial roots with a discrete set of angles of inclination of the curve. The roots of the polynomial are selected to meet the requirements (1). The example of the desired logarithmic amplitude-frequency characteristics shown in Fig. 3. The equation of this piecewise-linear functions can be written as:

12

y = A_{r} + B_{r} l g ω, ω_{r} < ω < ω_{r + 1}, r = 0,1, . . ., n + 1,

where $ω_{r}$ , $r = 1,2, \dots, n$ – polynomial roots, $ω_{0} < ω_{1}$ and $ω_{n} < ω_{n + 1}$ . $B_{r}$ coefficients in this system of equations are defined as follows: $B_{0} = 0$ , $B_{r} = B_{r - 1} + B$ , where $B$ = –40 – number characterizing the logarithmic slope of the asymptotic frequency response for a conservative level of 40 dB per decade, i.e. $B_{r}$ = –40∙ $r$ , $r = 0,1, \dots, n$ .

Ordinate a meeting point for the two lines, given in the form $y_{1} = A_{1} + B_{1} x$ and $y_{2} = A_{2} + B_{2} x$ written as:

13

x = \frac{A_{1} - A_{2}}{B_{2} - B_{1}} .

In our case, $x = l g ω_{r}$ . Then, to determine the values of $A_{r}$ (12) to modify the expression (13):

14

l g ω_{r} = \frac{A_{r - 1} - A_{r}}{B_{r} - B_{r - 1}} = \frac{A_{r - 1} - A_{r}}{- 40}, r = 1,2, . . ., n,

when $ω_{0} \to 0$ , $A_{0} = 20 l g (1 / | a_{0} |)$ . From the last set of equations consecutively determined values of $A_{r}$ . After obtaining the specific values of the coefficients (12), we determine the numerical values of the logarithms of the characteristic polynomial $L^{'} (ω)$ .

To do this, you must select the frequency $ω_{i}^{'}$ , under which the value of the characteristic polynomial (2) will be located. Obviously, these values should be chosen from the condition of maximum approach, the asymptotic logarithmic amplitude-frequency characteristics of the real value. In this case, they are defined as follows:

15

l g ω_{i}^{'} = l g ω_{i} + ξ (l g ω_{i + 1} - l g ω_{i}), i = 1,2, . . ., n - 1 .

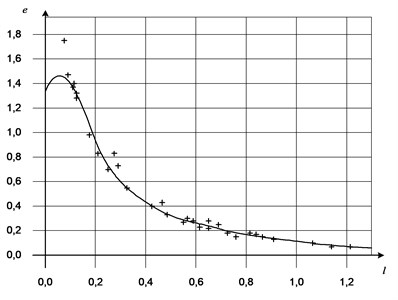
Experimentally, as a result of mathematical modeling, the value dependence of $ξ$ on $l = l g ω_{i + 1} - l g ω_{i}$ provided the difference in the minimum $L (ω) - L^{'} (ω)$ , as shown in Fig. 4. It is obvious that the value of $ξ$ hardly correlated to the distance along the axis between two logarithms of natural frequencies and should be chosen as equal to 0.5.

The value $ω_{n}^{'}$ need to be chosen as more than one order of magnitude greater than $ω_{n}$ , i.e. $l g ω_{n}^{'} = S + l g ω_{n}$ , where $S > 1$ . This condition is based on the maximum approach to the asymptotic logarithmic amplitude-frequency characteristics of the real. From these requirements it follows that $ω_{0}^{'} = 0$ .

Substituting the values of $ω_{i}^{'}$ in the expression (12), and replacing $y = - 20 l g |D (p)|$ we obtain the following system of equations:

16

- 20 l g |D (p)| = A_{i} + B_{i} l g ω_{i}^{'}, i = 0,1, . . ., n .

The consideration of imperfectly matching of the real logarithmic frequency response with its asymptotic approximation is necessary (16) is rewritten as:

17

- 20 l g |D (p)| = A_{i} + B_{i} l g ω_{i}^{'} + 20 e_{i},

where $20 e_{i}$ – some amendments. And let’s assume that $e_{0}$ = 0 and $e_{n}$ = 0. For $e_{i}$ , $i = 1,2, \dots, n - 1$ the experimental approximation of its dependence on the magnitude of the difference of the logarithms of nearby roots of the characteristic equation has been found as follows:

18

e_{i} = \frac{1}{17,4 l^{4} - 33,8 l^{3} + 26,5 l^{2} - 2,5 l + 0,74},

where $l = l g \frac{ω_{i + 1}}{ω_{i}}$ .

Fig. 5 shows this relationship with the experimentally obtained points. The degree of approximation in this case, $0.1 < l < 13$ is quite satisfactory. A slight variation of available values is explained by the quantization errors in digital simulation system of computers.

The construction results of a logarithmic frequency response to the desired frequency characteristics are numerical values of a polynomial (2) $L_{i}$ , at frequencies $ω_{i}^{'}$ (15).

On this basis, to build a system of $n + 1$ equations that can be solved with respect to $n + 1$ independent coefficients of the polynomial. In the particular case of:

19

L_{0} = a_{4} p_{0}^{4} + a_{3} p_{0}^{3} + a_{2} p_{0}^{2} + a_{1} p_{0} + a_{0},

L_{1} = a_{4} p_{1}^{4} + a_{3} p_{1}^{3} + a_{2} p_{1}^{2} + a_{1} p_{1} + a_{0},

L_{2} = a_{4} p_{2}^{4} + a_{3} p_{2}^{3} + a_{2} p_{2}^{2} + a_{1} p_{3} + a_{0},

L_{3} = a_{4} p_{3}^{4} + a_{3} p_{3}^{3} + a_{2} p_{3}^{2} + a_{1} p_{3} + a_{0},

L_{4} = a_{4} p_{4}^{4} + a_{3} p_{4}^{3} + a_{2} p_{4}^{2} + a_{1} p_{4} + a_{0}

Fig. 4Magnitude dependence of ξ on l=lgωi+1-lgωi provided minimum difference Lω-L'ω

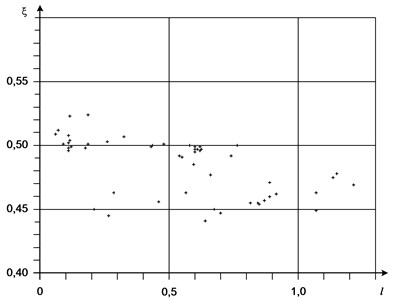
Fig. 5Approximation of amendments to values of asymptotic logarithmic frequency response of value of l=lgωi+1-lgωi

The solution results of system (19) are the numerical values of the coefficients of the polynomial (2), which were previously recorded in general terms of the parameters of synthesized transport mechanism of tape units (3).

2. Definition of tape transport mechanism parameters

The system of Equations (3) generally is not soluble because the number exceeds the number of unknown parameters of the system of equations. Therefore, it is necessary to redefine it by assigning specific numerical values of some of the unknown. In particular, in the tape transport mechanism synthesized always have nodes which parameters must be set in advance. For example, in order to unify with other designs or technological limitations. The system (3) will be assumed to be known in advance with the following parameters $k_{1}$ , $m_{3}$ , $m_{4}$ , $k_{7}$ . The values of the other five remaining parameters $m 1$ , $m 2$ , $k 5$ , $k 6$ , $k 8$ are determined by solving the system of equations (3) by conventional methods. These settings of links tape transport mechanism are optimal in terms of lack of resonance phenomena.

As an example, define one of the possible solutions of the system (3). Suppose that $F_{1}$ = 10.0 Hz, $F_{1}$ = 38.5 Hz, $F_{3}$ = 222 Hz, $F_{4}$ = 380 Hz. Also, we will ask the already known system parameters $k_{1}$ = 17200 N/m; $m_{3}$ = 0.435∙10^-2 kg; $m_{4}$ = 0.435∙10^-2kg; $k_{7}$ = 8200 N/m.

Table 1Characteristic equation coefficients

$N$	$F_{i}$ , Hz	$ω_{i}^{2}$	$C_{r}$	${\tilde{a}}_{r}$	$a_{r}$	$ε_{r}$
0	–	–	2.56∙10²¹	1.002∙10¹⁶	1.000∙10¹⁶	0.20 %
1	10.0	3.95∙10³	–6.94∙10¹⁷	–2.718∙10¹²	–2.740∙10¹²	0.80 %
2	38.5	5.85∙10⁴	1.16∙10¹³	4.588∙10⁷	4.562∙10⁷	0.75 %
3	222	1.94∙10⁶	–7.71∙10⁶	–3.017∙10¹	–3.026∙10¹	0.30 %
4	380	5.70∙10⁶		3.914∙10^-6	3.914∙10^-6	0 %

Table 2Characteristic equation coefficients by logarithmic amplitude-frequency response

$N$	0	1	2	3	4
$F_{r}$	–	10.0	38.5	222	380
$ω_{r}$	–	62.83	241.9	1395	2388
$l g ω_{r}$	–	1.798	2.384	3.144	3.378
$A_{r}$	–320	–248	–152.7	--26.95	108.2
$B_{r}$	0	–40	–80	–120	–160
$l g ω_{r}^{'}$	0	2.091	2.764	3.261	4.378
$e_{r}$	0	5.52	3.90	16.32	0
$L_{r}^{'}$	–320	–326.1	–369.9	–402.0	592.3
${\tilde{a}}_{r}$	1∙10⁶	–2.611∙10¹²	4.461∙10⁷	–2.990∙10¹	3.935∙10^-6
$a_{r}$	1∙10⁶	–2.740∙10¹²	4.562∙10⁷	–3.026∙10¹	3.914∙10^-6
$ε_{r}$	0 %	4.70 %	2.21 %	1.18 %	0.62 %

We define the coefficients of the Equation (8) by the formula $C_{r}$ (7), where $ω_{i} = 2 π F_{i}$ . We define a priori coefficient $k$ = 3.91∙10^-6.

The calculation results are summarized in Table 1. This table also shows the true values of the coefficient $a_{r}$ of Equation (2) with the roots, resulting from multiple iterative selection on a computer, and the relative error in calculating the coefficients ${\tilde{a}}_{r}$ by the proposed method.

The procedure for determining the coefficients of the Equation (2) using a logarithmic amplitude-frequency characteristic of the same initial conditions is given in Table 2.

A comparative analysis of the relative error in determining the numerical values of the coefficients of the characteristic equation shows that the first method is more precise than the second one. However, if low-frequency components of the spectrum of the natural frequency synthesized in the system are the most dangerous, the second method is more preferable because an error in determining the coefficient $a_{0}$ , the strongest influence on the low-frequency part of the spectrum in this case is zero. Substituting the numerical values of the coefficients of ${\tilde{a}}_{r}$ , e.g., from Table 1, in the Equations (3) and the known system parameters, the other parameters are defined: $m_{1}$ = 0.34 kg; $m_{2}$ = 0.6 kg; $k_{5}$ = 0.35∙10^-2 N/m; $k_{6}$ = 8350 N/m; $k_{8}$ = 8500 N/m.

3. Conclusion

The created synthesis method of tape transport mechanism by successive solutions of two systems of algebraic equations in which variables are the coefficients of the characteristic polynomial and mechanical parameters of the tape transport mechanism with a priori given spectrum of eigenfrequencies.

We propose two ways to determine the numerical values of the characteristic polynomial coefficients through a priori given natural frequencies:

- Through the use of direct eigenvalues;

- By building the desired logarithmic frequency response of the system and determining the numerical values of a polynomial at frequencies located between the natural frequencies.

We prove that the first way to determine the coefficients characteristic polynomial more precisely of the second order of magnitude. However, if more accurate accounting of the low frequency components of the spectrum is required, then the second method is more preferable and more efficient.

References

Nistyuk A. I., Lyalin V. E., Elkin V. S. A formal description of the algorithm and analysis diacoptical topological models of dynamic systems with lumped parameters. Vestnik ISTU: Mathematical Modeling of Radio-Electronic Means of Telecommunication Systems, 2002, p. 35-42, (in Russian).

Search CrossRef
Lyalin V. E., Elkin V. S. Analysis of methods of spectral synthesis of conservative dynamical systems. Vestnik ISTU: Mathematical Modeling of Radio-Electronic Means of Telecommunication Systems, Izhevsk, 2002, p. 29-35, (in Russian).

Search CrossRef
Nistyuk A. I., Elkin V. S. Methods and algorithms for the synthesis of the dynamic systems of the frequency spectrum. Vestnik ISTU: Mathematical Modeling of Radio-Electronic Means of Telecommunication Systems, Izhevsk, 2002, p. 28-33, (in Russian).

Search CrossRef
Nistyuk A. I., Elkin V. S. Algorithms analysis diacoptical topological models plots tape carrier-playback recording equipment. Vestnik ISTU: Intelligent Information Technology in Telecommunications and Telemetry, 2002, p. 34-38, (in Russian).

Search CrossRef
Chua L. O., Chen Li-Kuan Diacoptic and generalized hybrid analysis. IEEE Transactions CAS, Vol. 23, Issue 12, 1976, p. 694-705.

Search CrossRef

About this article

Received

21 August 2016

Accepted

25 August 2016

Published

07 October 2016

SUBJECTS

Modal analysis

Keywords

characteristic equation

optimum values of own frequencies

priori defined borders resonance hazardous areas

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.