Vibration suppression of rotating nonlinear beam by nonlinear energy sink

1. Introduction

Vibration suppression of rotating beam is an important issue for safety running of rotating machinery. Rotating machinery is usually subjected to complex excitation and dynamic stiffness due to high speed rotation. As we all know, linear vibration absorber can be useful for a narrow frequency zone which is near the resonant frequency. Recently, Vakakis et al. [1] proposed a new nonlinear absorber named nonlinear energy sink (NES) which contained a linear damping, a nonlinear stiffness and a small mass. They found that NES could absorb steady state vibration energy from the linear oscillator over a relatively broad frequency range.

Vibration suppression of beam by NES has been a very important issue in recent studies. Georgiades and Vakakis [2] provided numerical evidence of targeted energy transfer from a linear flexible beam under shock excitation to a NES. Ahmadabadi and Khadem [3] investigated the bifurcations and topological structure of nonlinear normal modes of two types of coupled NES on energy suppression of a cantilever beam under shock excitation. Parseh et al. [4-5] studied order three steady state dynamics of damped linear harmonically excited beams coupled with a NES. Kani et al. [6] investigated targeted energy transfer from a nonlinear beam with simply supported ends to a NES. Bab et al. [7] used a NES to mitigate vibration of a rotating beam under an external force. The Hopf bifurcation, saddle-node bifurcation and strongly modulated responses were found in this system.

In previous researches, vibration suppression of a rotating nonlinear beam under harmonic excitation by using NES has not been investigated yet. Also, finding the suitable parameters of NES for vibration suppression of rotating beam by analytical analysis is significant. All these studies are presented in this paper.

2. Dynamical model

Consider a rotating nonlinear beam coupled with a nonlinear energy sink, as shown in Fig. 1. The length of the beam is $l$, and $\rho$ is the density, $E$ is the Young’s modulus, $h$ and $b$ are the depth and width of the cross section of the beam respectively. The coordinate set $oxy$ is fixed to the beam with a constant rotating speed $\mathrm{\Omega }$. The vibration of the beam in y direction is considered in this paper. To suppress the vibration of the beam, a NES is fixed on the beam at $x_s$. The NES is a small mass $m_s$ coupled with the beam by a nonlinear stiffness $k_s$ and linear damping $c_s$. The displacement of this small mass in y direction is $y_s$.

Fig. 1Rotating nonlinear beam coupled with a NES

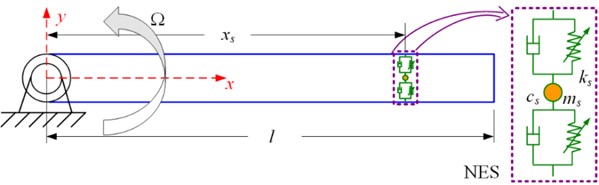
The governing differential equations of motion of the rotating nonlinear beam-NES system are derived by applying the quasi-Hamilton’s principle which requires the expressions for potential, kinetic and dissipate energies of the dynamic system as fundamental prerequisites.

It is convenient to introduce the following dimensionless parameters: $t=\gamma \tau$, $\stackrel{-}{\omega }=\omega \gamma$, $\stackrel{-}{\mathrm{\Omega }}=\mathrm{\Omega }\gamma$, $y=\stackrel{-}{y}l$, $x=\stackrel{-}{x}l$, $y_s={\stackrel{-}{y}}_{s}l$, $x_s={\stackrel{-}{x}}_{s}l$, $\gamma =l^2\sqrt{\rho A/EI}$. Applying the Galerkin method, and setting $q_s={\stackrel{-}{y}}_s-\stackrel{-}{y}({\stackrel{-}{x}}_s,\tau )$, the vibration equations can be rewritten as:

where ${\omega }_0^2={\int }_0^1\mathrm{\Phi }\left(\stackrel{-}{x}\right)\mathrm{\Phi }\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}\left(\stackrel{-}{x}\right)d\stackrel{-}{x}$, ${\omega }_d^2={\int }_0^1\mathrm{\Phi }\left(\stackrel{-}{x}\right)\left[\frac{1}{2}\left({\stackrel{-}{x}}^2-1\right)\mathrm{\Phi }\mathrm{\text{'}}\mathrm{\text{'}}\left(\stackrel{-}{x}\right)+\stackrel{-}{x}\mathrm{\Phi }\mathrm{\text{'}}\left(\stackrel{-}{x}\right)-\mathrm{\Phi }\left(\stackrel{-}{x}\right)\right]d\stackrel{-}{x}$, $\lambda ={\int }_0^1\left(\frac{3A{l}^2}{I}{\mathrm{\Phi }\mathrm{\text{'}}}^2\left(\stackrel{-}{x}\right)\mathrm{\Phi }\mathrm{\text{'}}\mathrm{\text{'}}\left(\stackrel{-}{x}\right)\right)d\stackrel{-}{x}$, $\epsilon =\frac{m_s}{\rho Al}$, $\zeta =\frac{c_s\gamma }{m_s}$, $\eta =\frac{k_s{\gamma }^2{l}^2}{m_s}$, $\stackrel{-}{f}=\frac{{\gamma }^{2}f}{\rho Al}{\int }_0^1\mathrm{\Phi }\left(\stackrel{-}{x}\right)d\stackrel{-}{x}$.

3. Analytical analysis

In order to solve the periodic response of Eq. 2 which is two DOF nonlinear vibration equations, the harmonic balance method is used in following. The solution of Eq. 2 takes the periodic form:

Substituting Eq. 3 into Eq. 2, and collecting the coefficients of $\mathrm{s}\mathrm{i}\mathrm{n}(\stackrel{-}{\omega }\tau +{\theta }_s)$ and $\mathrm{c}\mathrm{o}\mathrm{s}(\stackrel{-}{\omega }\tau +{\theta }_s)$, one obtains algebraic equations for $a$, $a_s$, $\theta$, and ${\theta }_s$:

Eliminating $\theta$, $a_s$ and ${\theta }_s$, yields:

where $P_i$ ($i$ = 1, 2,…, 9) is function of structural parameters of beam and NES. Thus, we can investigate the parameter influence on the vibration amplitude of the rotating beam.

4. Results for vibration suppression

In order to reveal the vibration suppression of rotating nonlinear beam by NES, the dynamic responses of the rotating beam coupled with a NES are studied for different NES parameters.

The main parameters used in this paper are chosen as: $l$ = 0.3 m, $\rho$ =7.85×10³ kg/m³, $E$ = 2.1×10¹¹ Pa, $b$ = 0.03 m, $h$ = 0.004 m, $f$ = 1 N.

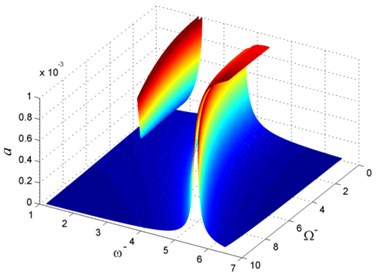
In order to verify that NES could suppress the vibration of rotating beam over a relatively broad frequency range. The vibration amplitude of beam with respect to external frequency and rotating speed is shown in Fig. 2. In this case, NES is installed on the end of the beam, and NES parameters are $\epsilon$ = 0.1, $\zeta$ = 0.1, and $\eta$ = 10⁶. The vibration amplitude near resonance is decreased due to NES under different rotating speed. The natural frequency of rotating beam is increased as the rotating speed increased. Thus, it can be seen that beam-NES system is resonance under different rotating speed, and NES can dissipate vibration energy transferred from rotating beam.

Fig. 2Vibration of rotating beam for different Ω-

The influences of structural parameters of NES (mass ratio $\epsilon$, non-dimensional damping $\zeta$, non-dimensional nonlinear stiffness $\eta$), and NES location ${\stackrel{-}{x}}_s$ on vibration suppression are investigated in the following. The NES parameters are vary, the non-dimensional rotating speed is chosen as 1, and the other parameters are chosen as before.

Figure 3 presents the amplitude of the beam in parameter spaces $(\epsilon ,\stackrel{-}{\omega })$ when $\zeta$ = 0.1, $\eta$ = 10⁶, and ${\stackrel{-}{x}}_s=1$. When $\epsilon$ = 0, the vibration of the beam shows soft-spring type due to the nonlinearity of beam. When NES is located on the beam, the vibration of the system shows hard -spring type. The vibration of the beam is suppressed greatly as the mass ratio increased. Moreover, two more vibration solutions, induced by the NES, appear in low frequency zone.

Figure 4 shows the amplitude of the beam in parameter spaces $(\zeta ,\stackrel{-}{\omega })$ when $\epsilon$ = 0.1, $\eta$ = 10⁶, and ${\stackrel{-}{x}}_s=1$. When NES damping is small, the vibration of the nonlinear beam-NES system shows hard-spring type. As the NES damping increased, the amplitude jumping phenomena disappears, and the amplitude of the beam is decreased greatly.

Figure 5 presents the amplitude of the beam in parameter spaces $(\eta ,\stackrel{-}{\omega })$ when $\epsilon$ = 0.1, $\zeta$ = 0.1, and ${\stackrel{-}{x}}_s=1$. When the nonlinear stiffness of NES is small, NES is almost independently on the vibration of beam. When the nonlinear stiffness of NES is increased, the vibration characteristic of nonlinear beam-NES system is changed from soft-spring type to hard-spring type, and two more vibration solutions appear in the low frequency zone.

Fig. 3Vibration of rotating beam for different ε

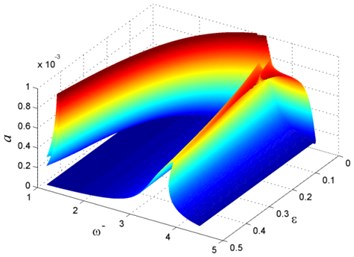
Fig. 4Vibration of rotating beam for different ζ

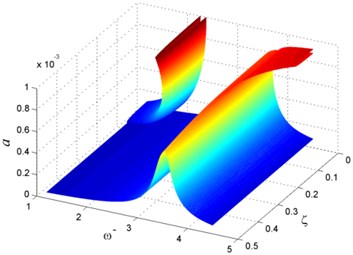
Fig. 5Vibration of rotating beam for different η

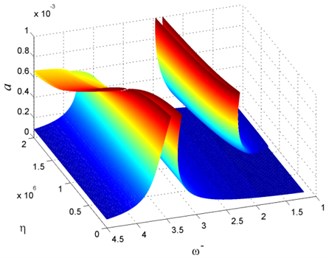
Fig. 6Vibration of rotating beam for different x-s

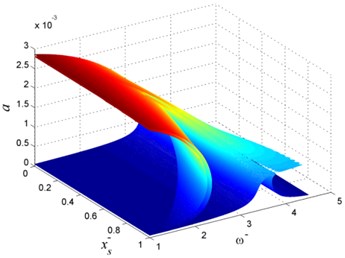
Figure 6 shows the amplitude of the beam in parameter spaces $({\stackrel{-}{x}}_s,\stackrel{-}{\omega })$ when $\epsilon$ = 0.1, $\zeta$ = 0.1, and $\eta$ = 10⁶. When NES is near to the fixed end, i.e., ${\stackrel{-}{x}}_s\to 0$, it leads to a poor performance for NES. When NES moves to the free end of the beam, the vibration characteristic of nonlinear beam-NES system is changed from soft-spring type to hard-spring type, and the vibration of the beam is decreased greatly, especially for resonant frequency.

5. Conclusions

A NES is used to suppress the vibration amplitude of a rotating nonlinear beam under an external harmonic force. The quasi-Hamilton’s principle and Galerkin method is applied to obtain the nonlinear vibration equations of beam-NES system. Then, harmonic balance method is used to acquire the analytic solution of vibration amplitude of beam. Lastly, a detailed study was presented in order to obtain an appropriate set of parameters for NES. Results show that the vibration of rotating beam is suppressed by NES under all rotating speed. And NES has a better performance as the rotating speed increased. Moreover, increasing the mass ratio, damping, nonlinear stiffness of NES or moving NES to the free end of the beam could induce a better performance of NES for vibration suppression of rotating beam.