Forced vibrations of vibro impact system with zero tightening with harmonic resonant excitation

1. Introduction

An important problem for engineering practical applications is investigated: namely dynamics of the system by taking into account dissipative forces and with an aim that those steady state vibrations should be stable and single valued. This is achieved by choosing suitable parameters of the system.

Forced vibrations of vibro impact system with zero tightening with harmonic resonant excitation are investigated. By using analytical – graphical methods characteristics of motions of the system are determined. Results of investigation for various typical parameters of the analysed system are presented and enable to determine suitable regimes for engineering practical applications.

Resonances and velocity jumps in nonlinear road-vehicle dynamics are investigated in [1]. Dynamics of two vibro-impact systems with energy sinks are analysed in [2]. Global asymptotic stabilisation of periodic nonlinear systems is described in [3]. Chatter in mechanical systems with impacts is analysed in [4]. Optimal control of periodic orbits of mechanical systems with impacts is investigated in [5]. The energy transfer mechanism of a single-sided vibro-impact nonlinear energy sink is described in [6]. Dynamics of particle impact with a wall is analysed in [7]. Frequencies of the planar flexible multibody system with clearances are investigated in [8]. Forced response of low-frequency pendulum mechanism is analysed in [9]. Nonlinear vibrations of a piecewise-linear system are investigated in [10]. The dynamics of a nonlinear energy harvester with multiple resonant zones are analysed in [11]. Sommerfeld effect in an oscillator with a reciprocating mass is investigated in [12]. Isolated resonances with nonlinear damping are analysed in [13]. A separate case of the vibro impact mechanism is investigated in [14].

The main objective of this paper is to present a model of a forced nonlinear vibro-impact system with zero tightening with harmonic resonant excitation. Such models can be useful in designing special types of nonlinear vibro-impact systems exhibiting stable and single valued regimes of motion. First, the model of the investigated system is described. Then results for various parameters of the investigated system are presented as well as dependence of characteristics of motion in steady state regime from the main parameters of the investigated system. The obtained results are useful in the process of optimal design of vibro impact mechanisms and their use in various engineering systems.

2. Model of the system

The investigated system is described by the following equation:

where $x$ denotes the displacement, $m$ is the mass of the system, $H$ is the coefficient of viscous friction, $C$ is the coefficient of stiffness, $F$ is the amplitude of the exciting force, $\omega$ is the frequency of excitation, $t$ is the time variable and the upper dot denotes differentiation with respect to the time. Also:

where $R$ is the coefficient of restitution and the superscript minus indicates the value before the impact, the superscript plus indicates the value after the impact. Such a vibro-impact system is not allowed to travel into the positive values of $x$ and is reverted back to the negative half-line after the impact.

The following notations are introduced:

By substituting Eq. (3) into Eq. (1) it is obtained:

By substituting Eq. (3) into Eq. (2) it is obtained:

3. Eigenvibrations with impacts

In this case it is assumed that:

Then the system is described by the following equations:

Spectrum of this nonlinear system is infinite and consisting from linear components. In this paper it is shown that steady state forced vibrations are located in the vicinities of those eigenfrequencies and they are single valued.

4. Forced steady state vibrations

Further dynamics of the system for typical parameters and taking into account the processes of steady state motions is investigated.

Case 1. In this case dynamics of the system for low frequency of excitation is investigated.

The following notation is introduced:

The following quantities are investigated in steady state periodic regimes of motion:

Graphical relationships are presented in Fig. 1.

Fig. 1Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 0.5, R= 0.7

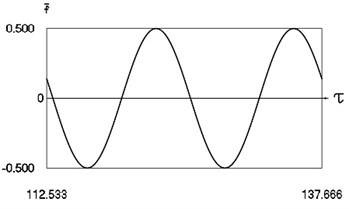
a) Harmonic function of excitation

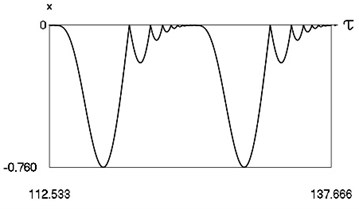
b) Displacement in periodic regime

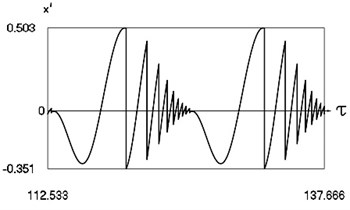
c) Velocity in periodic regime

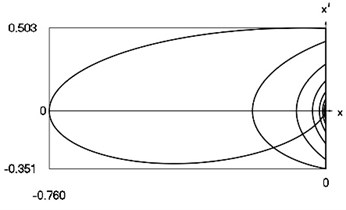
d) Representation in the phase plane: velocity as function of displacement in periodic regime

In Fig. 1 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for small value of frequency of excitation are presented. The results show that for small value of frequency of excitation multiple decaying impacts are observed.

When $\nu <1$ in steady state regime in one period of the function of excitation several impacts take place and with the decrease of frequency of excitation regimes of motion with the higher number of impacts take place. Regimes with decaying impacts are seen. Thus, cyclic motion takes place.

Case 2. In this case dynamics of the system for various values of coefficient of restitution is investigated.

Graphical relationships are presented in Fig. 2 and Fig. 3.

In Fig. 2 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for small value of coefficient of restitution are presented.

In Fig. 3 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for large value of coefficient of restitution are presented.

From mutual comparison of corresponding drawings of Fig. 2 and Fig. 3 the influence of the value of coefficient of restitution $R$ to the dynamic behavior of the investigated system is observed. From $x=x\left(\tau \right)$, $x\text{'}=x\text{'}\left(\tau \right)$, $x\text{'}=x\text{'}\left(x\right)$ as functions of their arguments at the values of parameters $h=$ 0, $f=$ –0.5, $\nu =$ 1 depending on the value of $R$ indicate that the quality of behavior of the system does not change, while the quantities change essentially.

Fig. 2Forced steady state vibrations in periodic regime for h=0, f= –0.5, ν= 1, R= 0.3

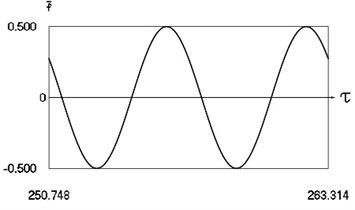
a) Harmonic function of excitation

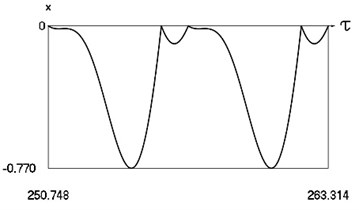
b) Displacement in periodic regime

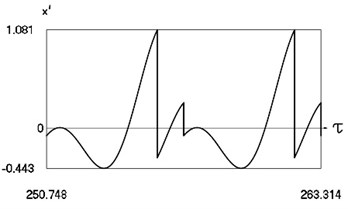
c) Velocity in periodic regime

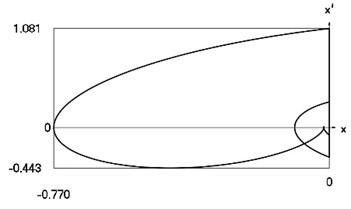
d) Representation in the phase plane: velocity as function of displacement in periodic regime

Fig. 3Forced steady state vibrations in periodic regime for h= 0, f= –0.5, ν= 1, R= 0.9

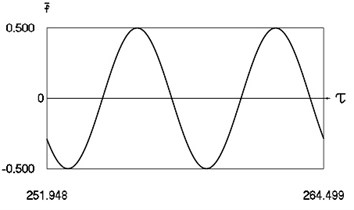
a) Harmonic function of excitation

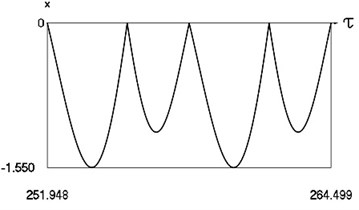
b) Displacement in periodic regime

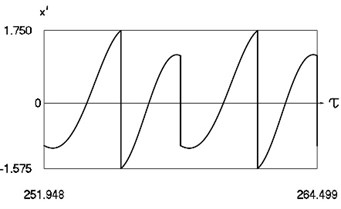
c) Velocity in periodic regime

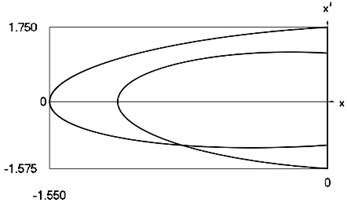
d) Representation in the phase plane: velocity as function of displacement in periodic regime

Characteristics of steady state motion as functions of coefficient of restitution are presented in Fig. 4.

From Fig. 4 the inter impact interval as function of coefficient of restitution, velocity before impact as function of coefficient of restitution, minimum displacement in the inter impact interval as function of coefficient of restitution are seen. The presented drawings show the influence of the value of the coefficient of restitution to the main characteristics of dynamic behavior of the investigated system. The intervals $T_{\tau 1}$, $T_{\tau 2},$ where $T_{\tau 1}+T_{\tau 2}=2\pi$, and the quantities ${{x\text{'}}^{-}}_{\tau 1}$, ${{x\text{'}}^{-}}_{\tau 2}$, $x_{m\tau 1}$, $x_{m\tau 2}$ at $h=$ 0, $f=$ –0.5, $\nu =$ 1 substantially depend from $R.$

Fig. 4Characteristics of steady state motion as functions of coefficient of restitution in periodic regime for h=0, f= –0.5, ν= 1

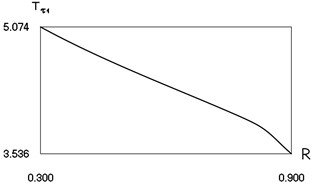
a) First inter impact interval

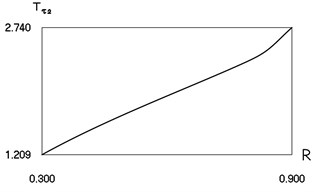
b) Second inter impact interval

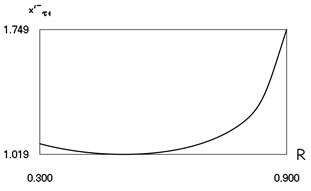
c) Velocity before first impact

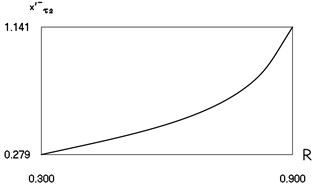
d) Velocity before second impact

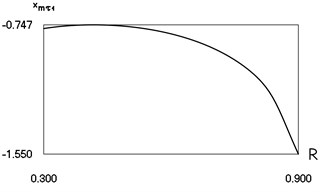
e) Minimum displacement in the first inter impact interval

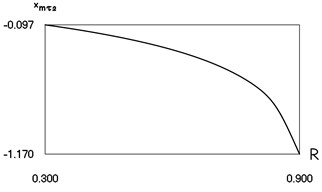
f) Minimum displacement in the second inter impact interval

Case 3. In this case dynamics of the system for various values of coefficient of viscous damping is investigated.

Graphical relationships are presented in Fig. 5 and Fig. 6.

In Fig. 5 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for small value of coefficient of viscous damping are presented.

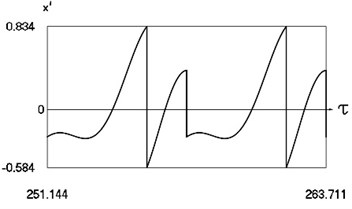
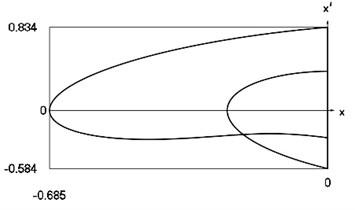
In Fig. 6 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for large value of coefficient of viscous damping are presented.

From mutual comparison of corresponding drawings of Fig. 5 and Fig. 6 the influence of the value of coefficient of viscous damping $h$ to the dynamic behavior of the investigated system is observed. From $x=x\left(\tau \right)$, $x\text{'}=x\text{'}\left(\tau \right)$, $x\text{'}=x\text{'}\left(x\right)$ as functions of their arguments at the values of parameters $f=$ –0.5, $\nu =$ 1, $R=$ 0.7 depending on the value of $h$ indicate that the quality of behavior of the system does not change, while the quantities change essentially.

Fig. 5Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 1, R= 0.7

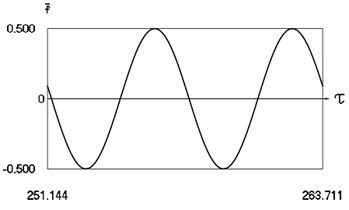
a) Harmonic function of excitation

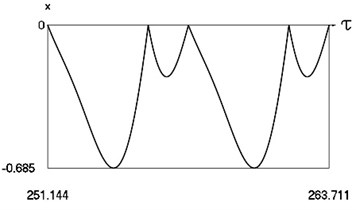
b) Displacement in periodic regime

c) Velocity in periodic regime

d) Representation in the phase plane: velocity as function of displacement in periodic regime

Fig. 6Forced steady state vibrations in periodic regime for h= 0.3, f= –0.5, ν= 1, R= 0.7

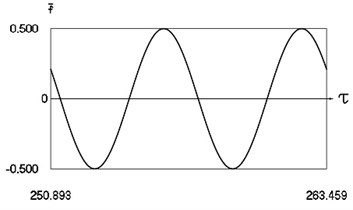
a) Harmonic function of excitation

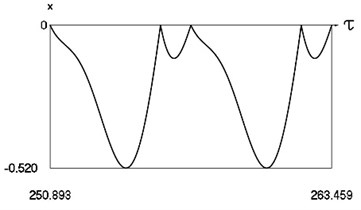
b) Displacement in periodic regime

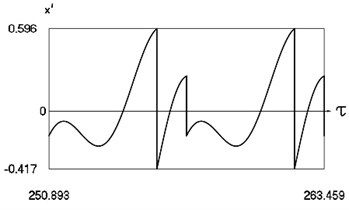
c) Velocity in periodic regime

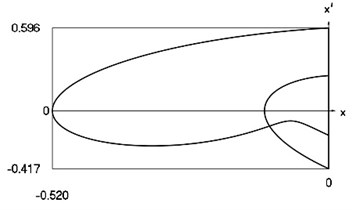
d) Representation in the phase plane: velocity as function of displacement in periodic regime

Characteristics of steady state motion as functions of coefficient of damping are presented in Fig. 7.

From Fig. 7 the inter impact interval as function of coefficient of viscous damping, velocity before impact as function of coefficient of viscous damping, minimum displacement in the inter impact interval as function of coefficient of viscous damping are seen. The presented drawings show the influence of the value of the coefficient of viscous damping to the main characteristics of dynamic behavior of the investigated system. The intervals $T_{\tau 1}$, $T_{\tau 2}$, where $T_{\tau 1}+T_{\tau 2}=2\pi$, and the quantities ${{x\text{'}}^{-}}_{\tau 1}$, ${{x\text{'}}^{-}}_{\tau 2}$, $x_{m\tau 1}$, $x_{m\tau 2}$ at $f=$ –0.5, $\nu =$ 1, $R=$ 0.7 substantially depend from $h.$

Fig. 7Characteristics of steady state motion as functions of coefficient of damping in periodic regime for f= –0.5, ν= 1, R= 0.7

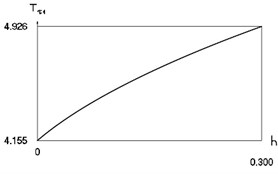
a) First inter impact interval

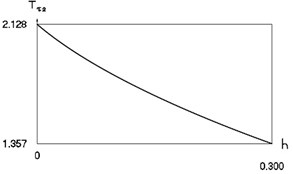
b) Second inter impact interval

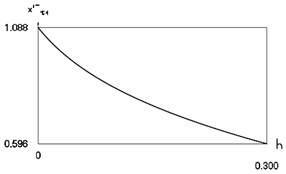
c) Velocity before first impact

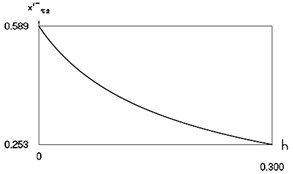
d) Velocity before second impact

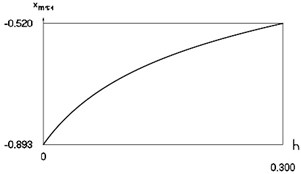
e) Minimum displacement in the first inter impact interval

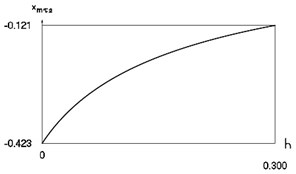
f) Minimum displacement in the second inter impact interval

Case 4. In this case dynamics of the system for various values of frequency of excitation is investigated.

Graphical relationships are presented in Fig. 8, Fig. 9, Fig. 10, Fig. 11 and Fig. 12.

Fig. 8Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 1.0485, R= 0.7

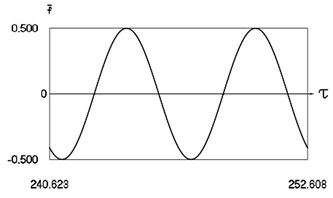
a) Harmonic function of excitation

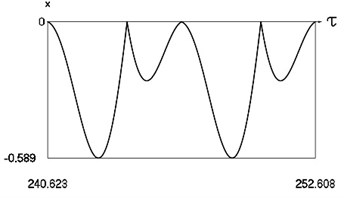
b) Displacement in periodic regime

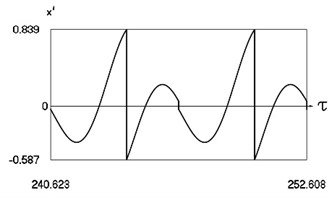
c) Velocity in periodic regime

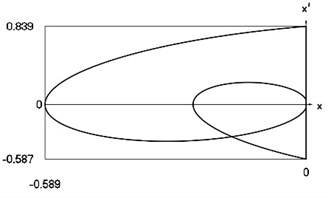
d) Representation in the phase plane: velocity as function of displacement in periodic regime

In Fig. 8 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for the value of frequency of excitation near to the lower border of the optimal zone of operation of the vibro impact system are presented. The results show that there are two different inter impact intervals.

Fig. 9Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 1.049, R= 0.7

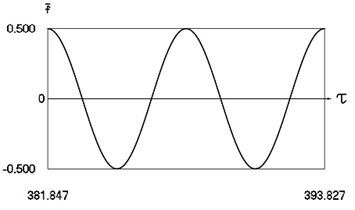
a) Harmonic function of excitation

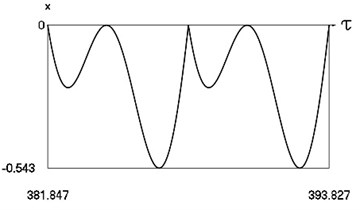
b) Displacement in periodic regime

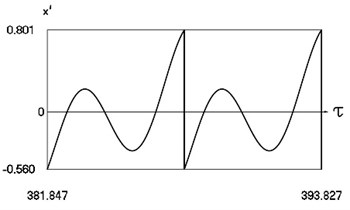
c) Velocity in periodic regime

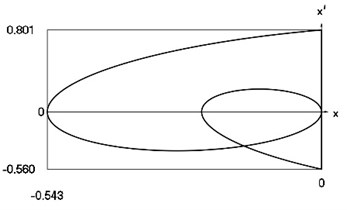
d) Representation in the phase plane: velocity as function of displacement in periodic regime

Fig. 10Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 2, R= 0.7

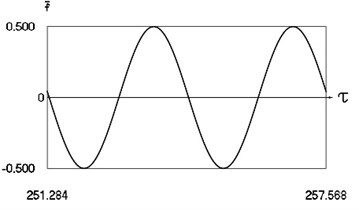
a) Harmonic function of excitation

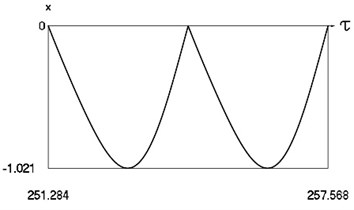
b) Displacement in periodic regime

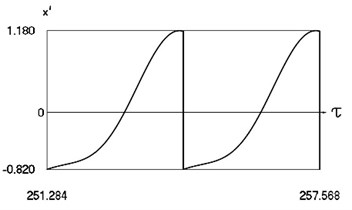
c) Velocity in periodic regime

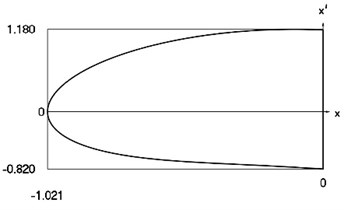
d) Representation in the phase plane: velocity as function of displacement in periodic regime

In Fig. 9 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for the value of frequency of excitation near to the lower border in the optimal zone of operation of the vibro impact system are presented. The results show that inter impact intervals are of the same type.

In Fig. 10 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for the value of frequency of excitation which is approximately optimal for operation of the vibro impact system are presented. The results show that absolute value of minimum displacement of the investigated system is large.

Fig. 11Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 2.665, R= 0.7

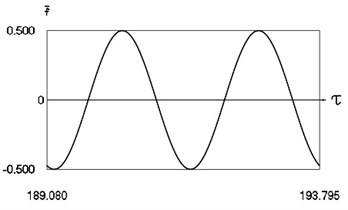
a) Harmonic function of excitation

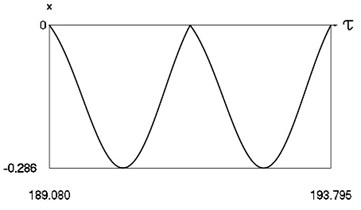
b) Displacement in periodic regime

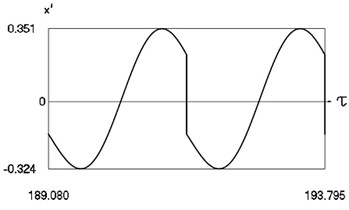
c) Velocity in periodic regime

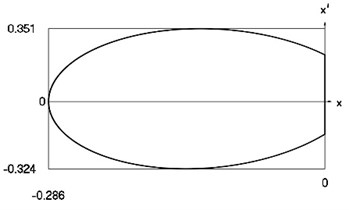
d) Representation in the phase plane: velocity as function of displacement in periodic regime

Fig. 12Forced steady state vibrations in periodic regime for h= 0.1, f= –0.5, ν= 2.67, R= 0.7

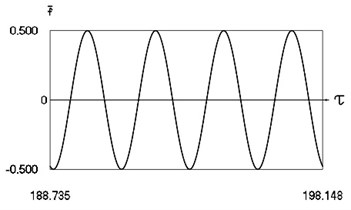
a) Harmonic function of excitation

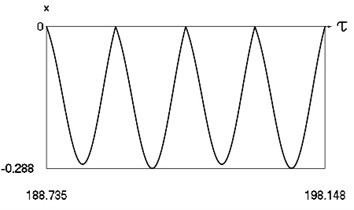
b) Displacement in periodic regime

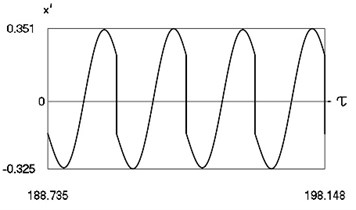
c) Velocity in periodic regime

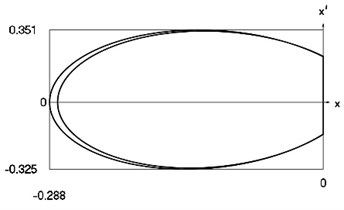
d) Representation in the phase plane: velocity as function of displacement in periodic regime

In Fig. 11 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for the value of frequency of excitation near to the upper border in the optimal zone of operation of the vibro impact system are presented. The results show that inter impact intervals are of the same type.

In Fig. 12 variation of the exciting force as function of time, variation of displacement as function of time, variation of velocity as function of time and dynamics of the investigated system in the phase plane for the value of frequency of excitation near to the upper border of the optimal zone of operation of the vibro impact system are presented. The results show that there are two different inter impact intervals.

From $x=x\left(\tau \right)$, $x\text{'}=x\text{'}\left(\tau \right)$, $x\text{'}=x\text{'}\left(x\right)$ as functions of their arguments at the values of parameters $h=$ 0.1, $f=$ –0.5, $R=$ 0.7 depending on the value of $\nu$ indicate that the quality of behavior of the system, as well as the quantities, change essentially.

Characteristics of steady state motion as functions of frequency of excitation are presented in Fig. 13 and Fig. 14.

Fig. 13Characteristics of steady state motion as functions of frequency of excitation in periodic regime for h= 0.1, f= –0.2, R= 0.7

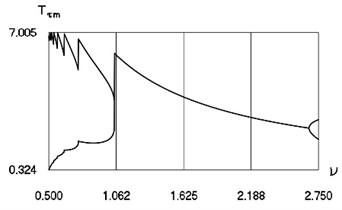
a) Minimum and maximum inter impact intervals

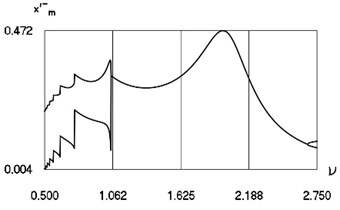
b) Minimum and maximum velocities before impact

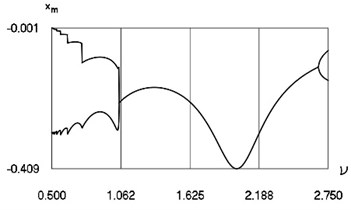
c) Minimum and maximum minimum displacements

From Fig. 13 the minimum and maximum inter impact intervals as function of frequency of excitation, minimum and maximum velocities before impact as function of frequency of excitation, minimum and maximum minimum displacements in the inter impact intervals as function of frequency of excitation for small in absolute value amplitude of excitation are seen. The intervals $T_{\tau m}$ and the quantities ${{x\text{'}}^{-}}_m,x_m$ at $h=$ 0.1, $f=$ –0.2, $R=$ 0.7 substantially depend from $\nu .$

From Fig. 14 the minimum and maximum inter impact intervals as function of frequency of excitation, minimum and maximum velocities before impact as function of frequency of excitation, minimum and maximum minimum displacements in the inter impact intervals as function of frequency of excitation for large in absolute value amplitude of excitation are seen. The intervals $T_{\tau m}$ and the quantities ${{x\text{'}}^{-}}_m$, $x_m$ at $h=$ 0.1, $f=$ –1.6, $R=$ 0.7 substantially depend from $\nu .$

The comparison of corresponding drawings from both previous figures shows the influence of the value of amplitude of excitation to the main characteristics of dynamic behavior of the investigated system. It can be noted that minimum and maximum inter impact intervals look the same for both values of amplitude of excitation. Optimal region of operation of the vibro impact system is also observed from those graphical representations.

Fig. 14Characteristics of steady state motion as functions of frequency of excitation in periodic regime for h= 0.1, f= –1.6, R= 0.7

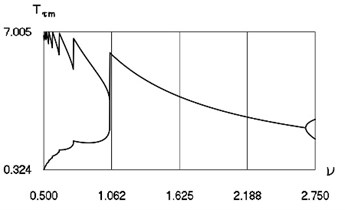
a) Minimum and maximum inter impact intervals

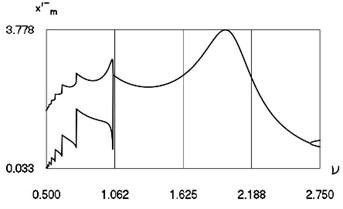
b) Minimum and maximum velocities before impact

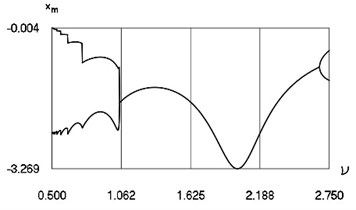
c) Minimum and maximum minimum displacements

5. Conclusions

Forced vibrations of vibro impact system with zero tightening with harmonic resonant excitation are investigated. Results for various typical parameters of the analysed system are presented. Also, dependence of characteristics of motion in steady state regime from the main parameters of the investigated system is investigated.

It is determined that optimal regimes are located at definite values of $\nu =\omega /p$, where $\omega$ is the frequency of the exciting force and $p$ is the partial eigenfrequency of the vibrating mass attached to the immovable foundation. Optimal regimes are in the zones about $\nu =$ 2, 4, 6, while higher values of $\nu$ are not useful in engineering applications. Further by changing the parameters of the system in those zones it is possible to determine the influence of the parameters to the size of separate zones.

Regimes of motion $\nu =1;\frac{1}{2};\frac{1}{4};\frac{1}{6};\dots$ are regimes with impacts having the character of decaying type. This is useful in some types of technological processes.

The obtained results can be exploited in the design of nonlinear dynamical systems with impacts. A noteworthy fact is that such nonlinear vibro-impact systems do posses single-valued and stable regimes of motion. Such a property can be useful in the design of elements of various machines, including manipulators and robots which are based on vibro impact systems.