Equilibrium forms branching of a nanolayers system

1. Introduction

In recent years, great interest of physicists, biologists and electrical engineers aroused the development of micro- and nanotechnology due to possibility of sensors production capable for nano- and microscale measurements of physical and biological parameters [1-6] such as molecular weight, quantum state, properties of biochemical reactions and others. Nanomechanical sensors have supplied sensitivity to extremely small forces and masses of order zeptonewtons (1 zN = 10^-21 N) and zeptograms correspondingly. Such sensitivity is caused by achievement of Mega and Giga-hertz frequency range of MEMS internal dynamic characteristics. For example, the silicone element 1 uM in length, 0.12 uM in width and with thickness of 0.075 uM has a natural frequency 1.03 GHz a $Q$-factor of order 10¹⁴ [1]. Not less widespread are micro sensors based on “pull-in” effect, which gave an opportunity to identify microchanges of external or internal physical characteristics [7].

In this paper we study the equilibrium forms branching of three parallel micro/nanolayers at direct current (Fig. 1). This type of structure is really feasible at the nanoscale [2]. This micro/nano structure can be used as a sensor of external and internal mechanical and electrical parameters or as a nanoresonator for measuring the mass of adhering nanoparticles [8, 9]. It is important to note that in the case of micro/nano schemes non-linear electromechanical interaction in them must be taken into account, as it is the basis of the mechanical or electrical characteristics identification.

Fig. 1Scheme of a system of nanolayers

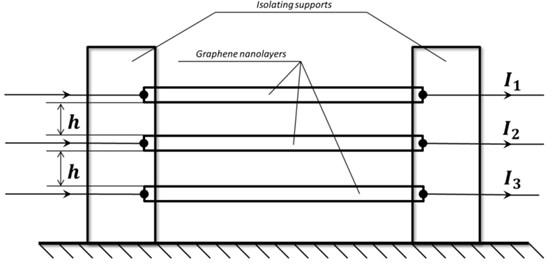
Physical parameters alteration can lead to symmetry breaking in the system, i.e. asymmetrical deflection of outermost layers and nonzero deflection of middle, initially neutral layer. By slow current intensity variation in one of outermost layers, initial symmetry of the system can be achieved, thus determining the parameters alteration which had occurred.

We will estimate graphene nanostrings (one-dimensional layers) parameters [2], at which significant interaction between layers is possible: layer length $l=$ 1000 nm, width $\delta =$ 10 nm, thickness $b=$0.3 nm. Thus, the resonant frequency of the vibrating string is 30 MHz with $Q~$100 [6]. Using the expression for the natural frequency $\stackrel{-}{\omega }$ of a stretched string, we obtain the required tension force $T={\rho }_{V}S{l}^2{\stackrel{-}{\omega }}^2/{\pi }^2=\mathrm{}$1,5∙10^-12 N. Introducing the parameter ${\lambda }^2={\mu }_0{I}^2/2\pi T{h}^2$ which characterizes the force interaction between layers, and assuming that its value is of order of the gap $h~\text{10}\text{nm,}$ we obtain the value of current $I_0=h\lambda /l\sqrt{\pi T/{\mu }_0}=$40 mkA$.$

2. Mathematical formulation

Introducing the notation of direct currents in layers in case of their equality $I_1=I_2=I_3=I=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$, we obtain the approximate expression for distributed attracting forces between layers excluding edge effects as $q=\frac{{\mu }_0{I}^2}{2\pi }\frac{\mathbf{r}}{r^2},$ where $\mathbf{r}$ – vector of distance between the layers which is directed normally to them [12]. Not taking into account the interaction between outermost layers, we get equilibrium equations in the form:

where $T$ is tension force, $q_{ij}$ – attractive force acting from $j$ conductor to $i$, $u_i$ – vertical deflections in layers; positive values of all forces and deflections correspond to vertical downwards direction.

In general case of different currents in layers attractive forces can be written in the form:

where $h$ is an initial gap between layers. We introduce dimensionless coordinates and displacements $s=x/l$, ${\nu }_i=u_i/h$ and main physical parameter ${\lambda }^2={\mu }_0{I}^2{l}^2/2\pi T{h}^2$. Thus we get system of equilibrium equations in non-dimensional form:

where the parameters ${\alpha }_1$, ${\alpha }_2$ characterize the deviation from symmetry, which can be caused, for example, by change of currents.

Assuming symmetrical deformed state relatively to central section of three layers (i.e., section normal to layers at $s=$0.5), we come to a conclusion that in every section through layers length the sum of first derivatives of deflections is equal to zero. Therefore, due to zero boundary conditions, sum of deflections of three layers is equal to zero through the length: $v_1+v_2+v_3=0.$

Introducing deflections differences $z_1=v_1-v_2$, $z_2=v_2-v_3$ and substracting Eq. (2) from Eq. (1) and Eq. (3) from Eq. (2), we obtain a system of two nonlinear Eq. (4):

with zero boundary conditions. Deflections of three layers in symmetrical case can be thus written in the form:

The achieved boundary value problem (Eq. (4)) in case of equal currents (${\alpha }_1={\alpha }_2$) allows symmetrical solution with non-deformed middle layer and outermost layers equally deflected one towards another: $v_2=0$, $v_1=-v_3$. Then we have $z_1=z_2=z$ and two equations in Eq. (4) transform to one: $z^{\text{'}\text{'}}+{\lambda }^2/1-z=0$ with zero boundary conditions $z\left(0\right)=0$, $z\left(1\right)=0.$ The above-named problem is equivalent to already considered problem of two nanostrings system equilibria at direct current [12]. Its bifurcation diagram contains two equilibrium forms (stable one with smaller amplitude and non-stable with bigger amplitude) at $\lambda <{\lambda }_{*}\approx$1.53, which disappear at $\lambda ={\lambda }_{*}$, what physically corresponds to coalescence of layers.

System of equations Eq. (4) allows for energy integral which is symmetrical relatively to $z_1$, $z_2$:

Searching partial solution $z_1=z_2=z\text{,}$ the energy integral is transformed to ${\left(z^{\text{'}}\right)}^2-2{\lambda }^2\ln \left(1-z\right)=h=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$, which correspond to the problem of two nanostrings.

3. Results and discussion

The obtained boundary value problem (Eq. (3)) is solved numerically, using the bvp4c Matlab subprogram. In Fig. 2 there are shown calculated symmetrical and non-symmetrical nanolayers equilibrium forms at different values of parameter $\lambda .$

Fig. 2Forms of equilibrium

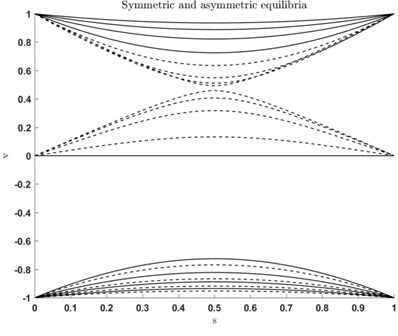
Analytical solution is achieved by Galerkin method solving system of Eq. (4) in assumption of deflection symmetry. Projection conditions of Galerkin method are obtained by searching the solution in the form $z_i=x_i\mathrm{s}\mathrm{i}\mathrm{n}\pi s$, $i=$1, 2 and integrating equations in Eq. (4), multiplied by $z_i$, along layers length:

Graphical solution of Eq. (7) for various values of $\lambda$ is shown in Fig. 3 (grey and dark lines keep with first and second equation in Eq. (7) correspondingly).

Fig. 3Graphical solution of Eq. (7) for various values of λ

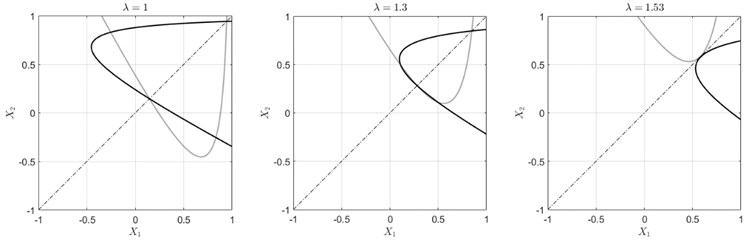
Numerically calculated bifurcation diagram of general system of equations (Eq. (3)) in case of equal currents is shown in Fig. 4, where deflection norms (maximum of absolute values of deflections along layer length) of one outermost ($v_1$) and middle ($v_3$) layers are presented in dependence of parameter $\lambda$. The notations $v_1$, $v_3$ and $v_5$ for top, middle and bottom layer result from rewriting ODE system (Eq. (3)) in normal form. Solution is obtained using AUTO 07P, a software for continuation and bifurcation problems [13].

Fig. 4Bifurcation diagram

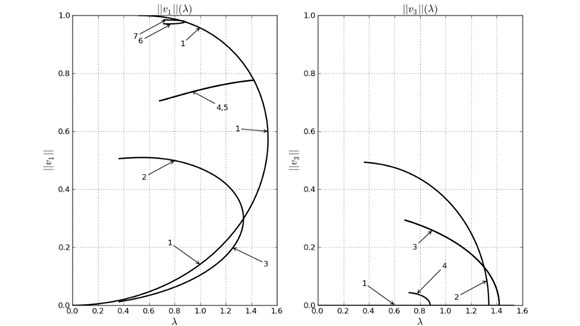
For $\lambda <{\lambda }_{**}\approx \text{1.34}$ there are three qualitatively different equilibrium forms: one stable form with non-deflected middle layer and symmetrically deflected outermost layers; and two non-stable forms with deflection of middle layer and smaller or bigger deflection of outermost layers (for example, for $\lambda \approx \text{0}$$‖v_1‖\approx$ 0.5, $‖v_3‖\approx$0.5, $‖v_5‖\approx$0 and vice versa for $v_1$ and $v_5$ – see Fig. 4, branches 1, 2, 3 for $‖v_1‖$ and branches 1, 2 for $‖v_3‖$). For ${\lambda }_{**}<\lambda <{\lambda }_{*}\approx$1.53 non-deflected state of middle layer becomes non-stable and aforenamed non-symmetrical forms don’t exist. For $\lambda >{\lambda }_{*}$ there are no equilibrium forms in the system, what physically corresponds to coalescence of layers. It is remarkable that for $\lambda <{\lambda }_{*}$ there also exist equilibria with outermost layers ($‖v_1‖$ or $‖v_5‖$) deflection norm higher than $0.5$ (see Fig. 4, branches 1,4-7 for $‖v_1‖$ and branches 1, 3, 4 for $‖v_3‖$). Among these forms exist non-symmetrical ones relatively to central section of layers, i.e. symmetry breaking occurs (see Fig. 4, branches 4, 5 for $‖v_1‖$ and branches 3 for $‖v_3‖$). Naturally, these forms could be found only by solving general boundary value problem (Eq. (3)), as the system Eq. (7) already contains assumption about central symmetry of solutions. It is notable that analytical solution by Galerkin method shown good agreement with numerical results.

4. Conclusions

In this work the branching theory was applied for the analysis of new type of nano- micro-electromechanical system. The obtained structure of branching can be used for determination of alteration of nano- and micro-scale physical parameters of the system.