Influence of the resonance characteristics of free-yaw small wind turbines on the performance

1. Introduction

Wind energy is one of the most perspective renewable energy sources. Small wind turbine is an attractive alternative for off-grid electrification, both as stand-alone utility and in combination with other energy technologies. One obstacle for using a wind power is the instability of its speed and direction, and, consequently, of output electric power. At the same time, the wind has not only a long-term and seasonal variability, but also changes its behavior within very short periods of time (instantaneous velocity pulsations, wind gusts, etc.).

Designers of a horizontal axis wind turbine (HAWT) yaw mechanisms are faced with a difficult decision. Use of a yaw-controlled rotor leads to increase in initial cost and decreases the reliability. On the other hand, a free-yaw rotor represents a high-risk design with unknown and random yaw characteristics [1].

The small wind turbines are often equipped by the passive mechanisms of yawing (free-yaw), such as lifting forces acting on a tail vane in the case of an upwind turbine or axial forces acting on the rotor in the case of a downwind turbine. The upwind free-yaw HAWT represents a torsional oscillation system. In fact, HAWT is a pendulum oscillator. The elastic element's stiffness of such system depends on wind speed and yaw angle.

The history of wind energy development is rife with accounts of yaw related problems. The most serious problems are structural failures due to yaw loans. Yaw-driven systems have had many instances of excessive yaw loads demerging the yaw drive mechanism. Many free-yaw rotors consistently operate at small (5°-15°) yaw errors and occasionally operate at lager yaw angles [1, 2].

Thus, a resonance excitation can appear during the HAWT operation that has a great influence on the performance. That excitation can induce amplified oscillations in the system that will lead to great output power losses and can cause damage of yaw drive mechanism. These processes and the effect of periodic unsteady fluctuations on the energy efficiency of wind turbines were devoted to the study, the results of which are presented below.

2. Wind turbine

The object of the research was considered experimental small upwind HAWT equipped by a free-yaw mechanism PE-250 (Fig. 1(а)). In wind turbines with free-yaw mechanism the aligning of rotor axis and wind direction carried out without any active controllers. This approach is simple and provides operational reliability, but, in the same time, may lead to unacceptable levels of mechanical loads [1].

The results of dynamic simulation of the HAWT PE-250 operation, by the method described in [3], showed a significant influence of yaw angle on the wind turbine rotor operational efficiency. (Fig. 1(b)). Thus, the yaw angle of 10° brings to a loss in generated power amount of about 4 %, then at 20° – already 14 %.

Fig. 1a) HAWT PE-250; b) theoretical output power generated by the wind turbine rotor (for the wind speed equals 6 m/s) depending on the yaw angle

а)

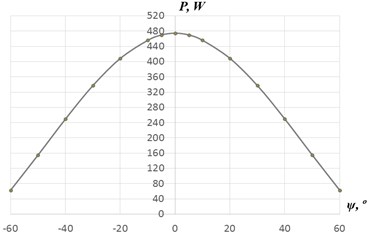
b)

3. Parameters of oscillation process in the HAWT yaw mechanism

The HAWT PE-250 in yaw operating conditions represents a torsional oscillator with elastic element of a lifting force acting on tail vane. Introducing such a system in general, the basic kinematic scheme of yawing HAWT can be obtained.

Like a torsional oscillator the HAWT performs torsional oscillation about the fixed yaw axis. The turning of the wind turbine nacelle around yaw axis is described by the general equation of dynamics [4, 5]:

where $M^T$ – the torsional torque about the rotation axis, $I$ – the moment of inertia of the wind turbine relative to the same axis, $d\omega /dt$ – the angular acceleration.

If wind direction changes relative to the nacelle axis the aerodynamic forces acting on the tail vane cause a torque. This torque tends to return the nacelle in position coaxially with new wind direction.

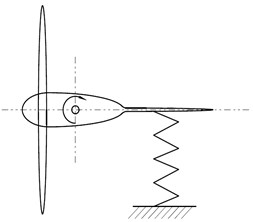
Factually, there is a pendulum oscillating system schematically shown on the Fig. 2. Stiffness of such system depends on the magnitude of wind speed and yaw angle.

Fig. 2Schematic of the pendulum oscillating system of HAWT in yaw operating conditions (top view)

The natural frequency of this system can be determined by the classical formula of torsional oscillations [6, 7]:

where $C$ – the torsional spring constant of HAWT yaw mechanism.

In case of the wind turbine yaw mechanism the value of torsional spring constant corresponds to the ratio of total torsional torque and yaw angle. The torque relative to the yaw angle, at the certain magnitude of wind speed, can be determined by the complex dynamic model presented in [3]. An example of that ratio for the wind speed of 6 m/s is presented on the Fig. 3.

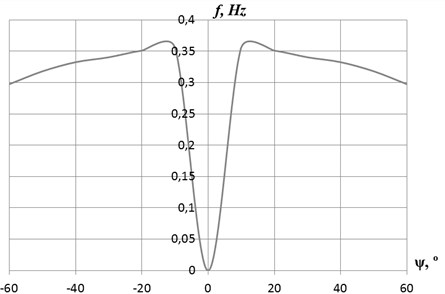
Based on the obtained ratio the natural torsional oscillation frequencies relative to the yaw angle can be determined. For a wind speed of 6 m/s, the graph of that ratio is presented on Fig. 4.

Fig. 3Total torsional torque MT depending on the yaw angle ψ (wind speed – 6 m/s)

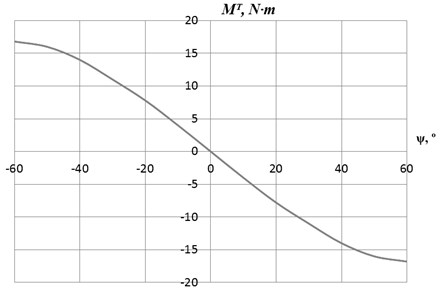
Fig. 4The natural oscillation frequencies of HAWT PE-250 depending on the yaw angle at the wind speed of 6 m/s

4. Experimental equipment

In order to determine the actually occurring yaw angles the field tests of the experimental free-yaw HAWT was performed. The considered experimental wind turbine represents a small-size machine. However, it has all the properties of the standard HAWTs with the passive mechanism of yawing. Thus, the test results can be applied to somewhat greater wind turbines. The technical characteristics of experimental HAWT are given in Table 1.

Comparing with the yaw mechanisms of small HAWTs from known manufacturers, the experimental wind turbine has a higher integral index of relative efficiency (Table 2).

A specialize measuring complex was developed to detect the operating parameters of experimental HAWT. The automatic braking system was installed in the spinner of nacelle. The system stops the rotor when the rotational speed exceeds the permissible value.

5. Results of the yaw angle measurements on an experimental HAWT PE-250

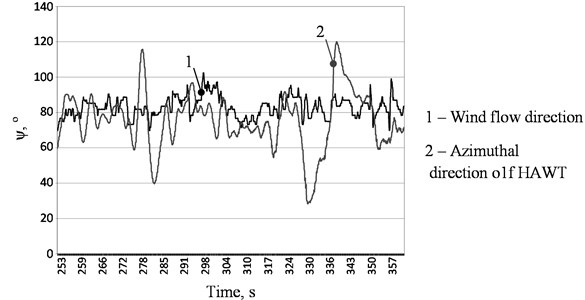
The field test results show that the conditions of wind flow misalignment (yaw error) are constantly present during the operation of the free-yaw HAWT. In some moments of time the value of misalignment achieves a significant amount. An example of recorded azimuthal parameters of the wind turbine nacelle and the wind flow are shown on Fig. 2. It could be seen that during the first period of time from 66 to 110 s the yaw error is relative small and on average equals 5.4° with frequency of wind turbine yawing equals 0.26 Hz. The frequency of wind flow oscillation is 0.46 Hz. From the other side the average yaw error during the second period of time from 110 to 165 s equals on average 25.6° with frequency of yawing equals 0.15 Hz. While the frequency of wind flow oscillation decreases to 0.32 Hz. It can be seen also that the wind speed is relatively constant. Thus it should be obvious that there are resonance excitations caused by the decreased frequency.

In some moments the coincidence of frequencies and phases leads to resonance oscillations of significant amplitudes. The coincidence of phases presented on Fig. 5 leads to a yaw error of about 40-50°. These behaviors of the HAWT will lead to great output power losses.

6. Conclusions

It can be concluded that, the upwind HAWT with a passive mechanism of yawing is constantly in conditions of azimuthal misalignment with wind flow direction. The experimental results show that the mean square deviation in the azimuthal directions is about 68.08 %. The arithmetic value of misalignment is equal to 11.6°. Consequently, the amount of decrease in efficiency for the angle 11.6° is equal to 7.1 %. Additionally, the misalignment of 40° caused by the resonance excitation, results in the efficiency decrease of 47.4 %. Thus the discovered values of misalignment angle caused by the resonance excitations lead to a significant decrease in efficiency and cause increase in operational loads. It reduces the life of equipment and makes it necessary to take in to account the resonance effects at the stage of designing.

Fig. 5An example of recorded azimuthal directions of wind flow and wind turbine with a high amplitude misalignment angle