Fault severity assessment of rolling element bearings based on bicoherence spectrum

1. Introduction

Rolling element bearings are key components of rotating machinery, and the faults related to the bearings are one of the major reasons that lead to machine breakdown [1, 2]. Hence, it is necessary to detect and diagnose these faults at an early stage.

Vibration signals collected from bearings carry the rich information on machine health conditions [3]. Vibration-based condition monitoring (VCM) is the most popular technique for the diagnosis of faults related to rotating machines because the machine vibration response is sensitive to any small structural or process parameter change [4]. Many vibration-based methods for faults diagnosis have been proposed in the past decades. Some success, indeed, have been achieved by these conventional techniques. However, most of them focus on fault identification, and limited work has been reported for fault severity assessment, which is also critical to make decision for maintenance actions [5, 6]. Therefore, it is very necessary to predict the trend of development of the bearing fault for the machine.

In recent years, thanks to the advantages that conventional methods can’t match, such as nonlinear system identification, phase information retention and Gussian noise elimination properties, Higher order spectrum (HOS) techniques have gained more and more attention. The bispectrum and the bicoherence spectrum are the two common HOS techniques. The bispectrum is complex and interpreted as measuring the amount of coupling between frequency components in signals. Hence the relationship between the different harmonic components of a signal can be observed in the bispectrum. Jyoti K. Sinha et al. did a lot research about the application of the bispectrum in rotating machinery [7, 8]. The bicoherence spectrum is the normalized forms of the bispectrum, and was also common used in machinery diagnostics [9, 10]. Fault-related signals usually show nonlinear terms. These terms cause nonlinear interactions between different spectral components of the signals. One of the most important nonlinear interaction is the quadratic phase coupling (QPC), i.e., the interaction between the original components $\left(f_1,{\phi }_1\right)$ and $\left(f_2,{\phi }_2\right)$ leads to the generation of the coupling components $\left(f_1{-f}_2,{\phi }_1-{\phi }_2\right)$ and $\left(f_1+f_2,{\phi }_1+{\phi }_2\right)$. While the bispectrum and the bicoherence spectrum are useful tool to detect the presence of QPC. In particular, the bicoherence spectrum may be used to discriminate between nonlinearly coupled components and spontaneously excited components, and to measure the fraction of energy due to QPC. Therefore, this paper attempts to assess the fault severity based on QPC by using the bicoherence spectrum.

2. Related work

3. Fault severity assessment based on bicoherence spectrum

In this paper, we attempt to make a quantitative analysis of different fault severities based on the bicoherence spectrum.

The steps of fault severity assessment are actually the procedures for computing the bicoherence spectrum. For an arbitrary input signal $x\left(t\right)$, with a record length $T=L∆t$, where $L$ is the number of samples and $∆t$ is the time between samples, its bicoherence spectrum estimation is given as the follow [11]:

(1) Divide the original data record into $M$ segments with the length of $N$ where $L=MN$. $x^{\left(i\right)}\left(l\right)$, $i=\mathrm{}$1,…, $M$ and $l=$ 1,…, $N$.

(2) Remove the mean value from each segment.

(3) Multiply with a window for each segment to reduce leakage.

(4) Calculate the Fourier amplitudes, using the FFT by:

(5) Estimate the squared bicoherence spectrum by:

(6) Gain the QPC features according to the squared bicoherence spectrum.

(7) Repeat the steps (1)-(6) for different fault severities and complete the fault severity assessment.

Note that one can reduce the number of calculations needed to compute the bicoherence spectrum by taking advantage of some symmetry properties of the bispectrum as well as physical limitations due to sampling [11]. The actual computation region can be confined to $0\le f_2\le 1/4f_s$ and $f_2\le f_1\le 1/2f_s-f_2$ where $f_1$ and $f_2$ are frequencies involving in coupling, and $f_s$ is the sampling frequency. The region forms a distinctive “triangle shape”, that can clearly be seen in Fig. 1.

4. Experimental validation and results

The vibration data analyzed in this paper were downloaded from the Case Western Reserve University Bearing Data Central [12]. As shown in Fig. 2, the rigs consist of a 2hp motor driving a shaft on which a torque transducer and encoder are mounted, and a dynamometer-load. The test bearings supporting the motor shaft at the drive end are 6205-2RS JEM SKF deep groove ball bearings. Single point faults with fault diameters 0.1778 mm, 0.3556 mm, 0.5332 mm were introduced to the ball, inner raceway and outer raceway of the test bearing using electro-discharge machining (EDM). Vibration data measured in the vertical direction on the housing of the drive-end bearing were collected using an acquisition system at a sampling frequency of 12 kHz for different bearing conditions.

Fig. 1The computation region of the bicoherence spectrum

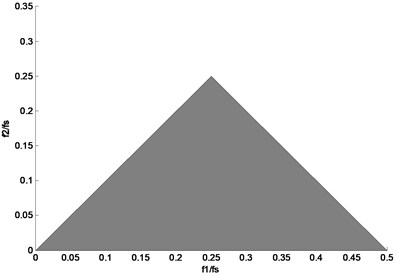
Fig. 2The experimental rig

The vibration signals of inner raceway fault (IRF) with three severity cases (case_1: 0.1778 mm, case_2: 0.3556 mm, and case_3: 0.5332 mm) and the normal case (case_0: Normal) at four rotating speeds (1730, 1750, 1772, 1797 rpm) are considered. The sampling frequency $f_s$ is 12 kHz. The contours of the squared bicoherence spectrum for four cases at two rotating speeds (1750, 1797 rpm) are shown in Fig. 3 and Fig. 4 respectively.

Fig. 3The contours of bc2f1,f2 at 1750 rpm: a) case_0, b) case_1, c) case_2, d) case_3

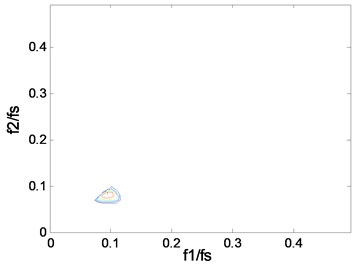
a)

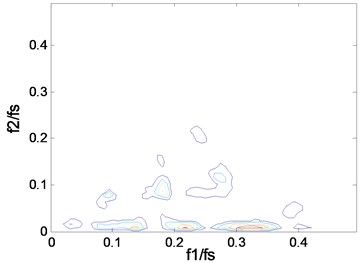
b)

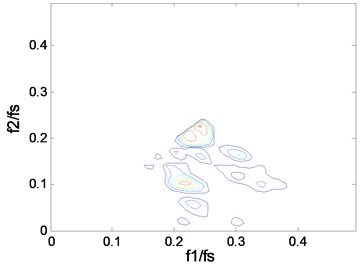
c)

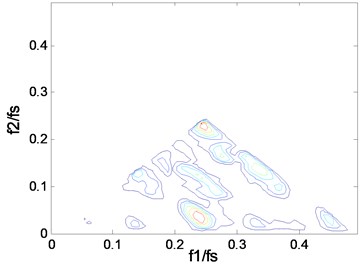
d)

Fig. 4The contours of bc2f1,f2 at 1797 rpm: a) case_0, b) case_1, c) case_2, d) case_3

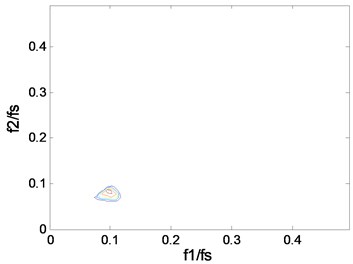
a)

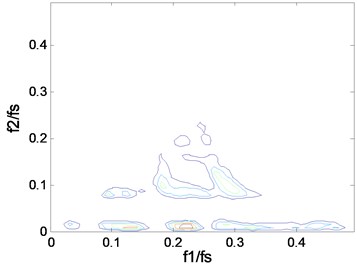
b)

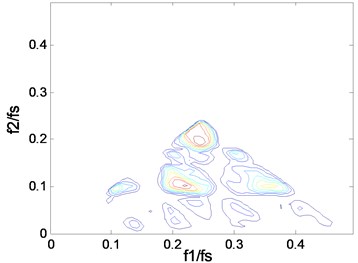
c)

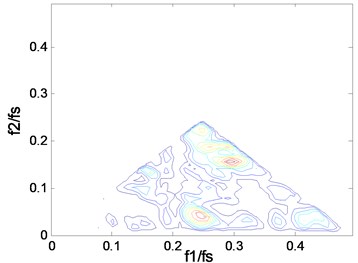
d)

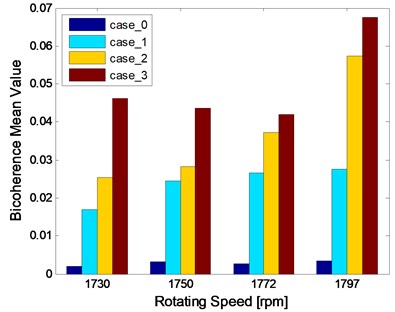
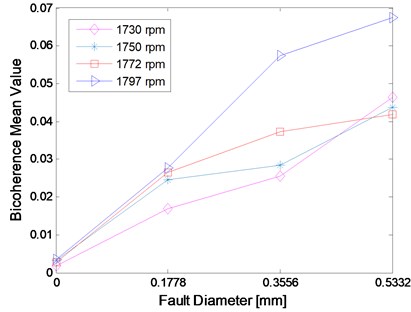
We know that $b_c^2\left(f_1,f_2\right)$ measures the percentage of energy at frequency $f_3$ due to coupling from $f_1$ and $f_2$. The contours show clearly what frequencies take part in the coupling. The “triangle shape” region is becoming more and more distinct when the fault severity increases, which indicates that the deepening fault severity results in more frequency pairs involving in coupling. In particular, there is only one frequency pair that takes part in coupling in the normal case and more peaks will appear in the fault cases, which can be used to separate the normal from the fault. A peak in $b_c^2\left(f_1,f_2\right)$ can be explained in a sum interaction between two frequencies to give a peak at $f_1+f_2=f_3$. Based on the description above, we know that the peak, namely the value of $b_c^2\left(f_1,f_2\right)$, is an important parameter that can reflect the fault severity. But one or other of the peaks can’t reflect the whole trend, the mean may be a good indicator. The mean value of the squared bicoherence in four cases at four rotating speeds are shown in Table 1. The corresponding bar chart and the trend curve are shown in Fig. 5. It can be clearly seen from Fig. 5 that the mean of $b_c^2\left(f_1,f_2\right)$ increases with the fault severity, meaning the fault is becoming more and more serious when the mean value increases. The change is relatively smooth from a light severity to a heavy one, but it changes sharply from the normal to the fault, such as, at 1772 rpm, the mean value is just 0.0027 in case_0, while it becomes 0.0266 in case_1 which is almost ten times of the former. This can be explained by the fact that the fault leads to more frequency pairs taking part in coupling, which results in more energy due to coupling. Therefore, the mean value of the squared bicoherence may be a strong indicator of the fault trend prediction.

Fig. 5The mean of bc2f1,f2 in different conditions: a) the bar chart, b) the trend curve

a)

b)

5. Conclusions

The fault severity assessment is very important for condition monitoring of rotating machinery at an early stage. The bicoherence spectrum is a useful signal processing technique and has excellent ability to detect nonlinearity, especially QPC. In this paper, we attempt to realize the quantitative detection of the fault on rolling element bearings and the assessment indicator based on the bicoherence spectrum is proposed. The experimental results show that the bicoherence spectrum is sensitive to different severities of fault. The mean value of the bicoherence spectrum may be a good indicator of fault severity assessment.