Abstract
Aiming at the vibration signal characteristics of multi-channel rolling bearing complex faults containing various shock components, a rolling bearing complex fault diagnosis model based on spatiotemporal intrinsic mode decomposition (STIMD) method and fast spectral kurtosis method was proposed. The spatiotemporal intrinsic mode decomposition method combines the signal atomic decomposition method with the idea of signal blind source separation. Through the fast independent component analysis and the nonlinear matching pursuit method of the established overcomplete dictionary base, various fault mode components are separated. The initial phase function selected based on the high kurtosis fault frequency band obtained by the fast spectral kurtosis method can better fit the bearing fault frequency domain characteristics, so that the spatiotemporal intrinsic mode decomposition method can more accurately separate various impact components in the vibration signal. The simulation model of bearing compound fault was established and the data collected from fault diagnosis experiment platform were used to verify that the STIMD method was effective in solving the problem of rolling bearing compound fault diagnosis. By analyzing the kurtosis changes under different signal noise ratio (SNR) conditions and comparing the simulation results with the fast independent component analysis method, it shows that the kurtosis index decomposed by the proposed method is more able to prove the existence of faults under the condition of low SNR, that is, the impact is completely covered by noise. Therefore, a spatiotemporal intrinsic mode decomposition method with fast spectral kurtosis optimization can solve the problem of blind source separation in the field of composite faults of multi-channel rolling bearings and realize composite fault diagnosis.
Highlights
- The spatiotemporal intrinsic mode decomposition method combines the signal atomic decomposition method with the idea of signal blind source separation.
- Through the fast independent component analysis and the nonlinear matching pursuit method of the established overcomplete dictionary base, various fault mode components are separated.
- The initial phase function selected based on the high kurtosis fault frequency band obtained by the fast spectral kurtosis method can better fit the bearing fault frequency domain characteristics, so that the spatiotemporal intrinsic mode decomposition method can more accurately separate various impact components in the vibration signal.
1. Introduction
With the development of intelligent manufacturing, industrial robot rotary arms, wind power generation, etc., it is more urgent to study rolling bearing fault diagnosis [1]. In recent years, the vibration signal acquisition technology is constantly improved, and the multi-channel signal acquisition equipment is constantly optimized. The vibration response caused by different materials is different [2-4]. The multi-channel signal can contain more bearing vibration information than the single channel signal, and can reflect more fault characteristics in the case of bearing compound fault. In engineering practice, vibration signals of mechanical faults are usually generated by multiple vibration sources, and the mixing matrix of each vibration source for mixed signals is unknown, so the problem of multi-channel fault diagnosis can be regarded as the problem of blind source separation [5, 6]. Bearing compound failure is more harmful to rotating machinery, which will lead to accelerated deterioration of equipment performance and even mechanical accidents. In complex faults, multiple faults often interact with each other, which makes it more complicated to separate multiple fault components from vibration signals.
Nowadays, blind source separation methods such as fast independent component analysis [7], De-noising Source Separation [8], singular value decomposition [9], principal component analysis [10] and tensor decomposition [11] are widely used in mechanical fault diagnosis. fast independent component analysis (FastICA) is a commonly used algorithm, which adopts fixed point and Newton iteration and has a fast convergence rate [12, 13]. However, the FastICA algorithm is very sensitive to signal gauss, resulting in unstable convergence, and can not accurately separate fault components. Hou and Shi [14] proposed data-driven time-frequency analysis (DDTFA) based on Adaptive Time-Frequency Analysis (ATFA). This method uses Newton iteration method to solve nonlinear problems and achieves the sparsest representation of signals in a dictionary composed of eigenmode functions. In 2020, Seth M. Hirsh et al. [15] proposed the concept of spatiotemporal intrinsic mode decomposition based on data driven time frequency domain analysis combined with the idea of blind source separation. This method is only applied the method to manipulate Gravitational waves from the LIGO experiment and Neural recordings from rodent hippocampus to effectively analyze its signal signatures, but not combined with mechanical fault diagnosis. The fast spectral kurtosis method is a common method to judge the position of impulse information in the frequency domain in the field of mechanical fault diagnosis. The spectral kurtosis can filter interference in the transient impact component, which improves the feature extraction effect and has great significance to enhance fault diagnosis accuracy of the rolling bearing [16]. The fast spectrum kurtosis algorithm can adaptively identify resonance bands of a signal, and fault characteristics can be extracted by analyzing the selected frequency bands. However, the bearing failure may be composed of various faults and the faults may be located in different resonant bands. Due to the interference between different fault components and noise, the weak components may be submerged when fast spectrum kurtosis is used to deal with compound fault signals [17, 18].
Bearing vibration signals can be decomposed into time modes and space modes from time scale and space scale, and the mode functions are extracted for analysis. The spatiotemporal intrinsic mode decomposition can make full use of the rich information contained in multidimensional data and extract the fault features of multidimensional data more comprehensively by using the established over-complete dictionary. Because the spatiotemporal intrinsic mode decomposition method is sensitive to the initial phase function, selecting the appropriate initial phase function by fast spectral kurtosis method [19] can realize the signal decomposition more accurately and quickly.
2. Spatiotemporal intrinsic mode decomposition theory
2.1. Fast independent component analysis
Independent component analysis is a method to solve the problem of blind source separation. It separates signals based on signal independence and can obtain the separation matrix when the source signal is unknown. It assumes that the source signals are statistically independent, the source signals are non-Gaussian distribution, and the mixed matrix is orthogonal. [20], where represents the mixed signal matrix, represents the mixed matrix, and represents the signal matrix after unmixing. If follows a Gaussian distribution, then a unique cannot be reduced. If is not Gaussian, then can be calculated by calculating , where represents the separation matrix. The central limit theorem states the conditions under which a large number of random variables approximate normal distribution [21, 22]. The central limit theorem is the main theoretical basis of the objective function [23]. By extension, it can be known that, compared with the source signal, the mixed signal received by the sensor is more gauss, and conversely, the non-gauss is weak. Therefore, the separation of mixed signals can be completed by performing non-Gaussian maximization operation on mixed signals. The independent component analysis algorithm [24] computes the and matrices using kurtosis or negative entropy by maximizing the non-Gaussian property of the source signal. Fast independent component analysis finds the direction of maximizing non-Gaussian measurement through projection pursuit [25].
The new signal is obtained by preprocessing the observed signal. is the row vector in the unmixing matrix . The FastICA algorithm maximizes the non-Gaussian property of a vector by a fixed point iterative algorithm. The most common evaluation function for non-Gaussianness is the approximation of negative entropy. The objective function of the FastICA algorithm is:
where is any non-quadratic function and is a Gaussian random variable whose mean value and unit error function is zero. means . Get the best value by maximizing in . When , the negative entropy is the highest, that is the maximum. Through the Lagrange multiplier algorithm, the objective function of the fixed point algorithm is [26]:
where is a constant, so the optimization problem is equivalent to:
where the function is the derivative of . The solution to the equation 3 is similar to the Newtonian iteration, that is, leaving the left side of the equation unchanged:
The gradient of is:
where for transpose. Since are independent sources, it can be assumed that the variance of is consistent. So the covariance of is equal to [27]:
The final iteration form of the fast ICA algorithm can be obtained by approximating the equation:
The weight vector is normalized after each iteration:
2.2. Nonlinear matching pursuit
Nonlinear matching pursuit (NMP) can be used to separate intrinsic mode function (IMF) from mixed signals instead of empirical mode decomposition. Assuming that the signal can be decomposed into a finite number of IMFs, the following problems can be solved:
where is assumed to contain the following interwave frequency modulated signals. can be known to be monotone by the invertible function theorem, and IMF is expressed by the function of :
If the and are smoother than , then is defined as an interwave frequency modulated signal. That is to say, the and are in the following set:
Among them , .
A signal that physically contains an interwave frequency modulation component can roughly correspond to the solution of the second-order differential equation:
where the and are the sufficiently smooth functions.
To sum up, the IMF dictionary with an interwave frequency modulation component is:
when the sum of is equal to the original signal , the quantity is minimum. For noisy signals the equality is replaced by inequality.
To solve the problem of NMP method minimization, an alternate scheme is proposed, that is, fixed minimization and then fixed updating . In the minimization calculation, projecting onto the surface is equivalent to applying a low-pass filter to the coordinates. The guess value of the initial phase function is generally .
2.3. Fast spectral kurtosis
Kurtosis is a dimensionless parameter index in the time domain which is very sensitive to the instantaneous characteristics of the signal. Kurtosis coefficient refers to the impact pulse generated at the defect of the working face when the working surface of rotating parts such as bearings is faulty. It is often used to detect the strength of the impact component in the vibration signal of rolling bearings [25]:
Spectral kurtosis (SK) is used to characterize the kurtosis value of each spectral line of the signal, so as to find the non-stationary components of the signal and their positions in the frequency domain [20]:
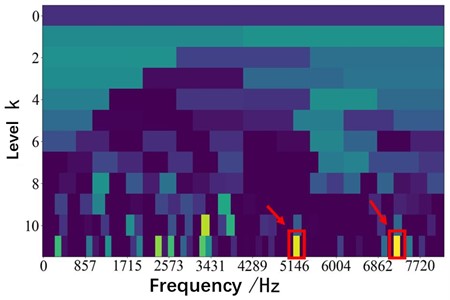
where is the mathematical expectation; is the complex envelope of the original signal at frequency . In order to obtain the transient components in the signal, the kurtosis value of each frequency band should be calculated to find the frequency band with the maximum kurtosis. In order to reduce the calculation time of spectral kurtosis significantly, fast spectral kurtosis calculation is carried out by using the 1/3 – binary tree filter banks to realize the fast calculation of spectral kurtosis of each sub-band, and the kurtosis value is represented according to the depth of the color graph [28].
2.4. Spatiotemporal intrinsic mode decomposition methods
The spatiotemporal intrinsic mode decomposition method establishes an over-complete dictionary base through empirical mode decomposition as the constraint condition of nonlinear matching pursuit method, which can effectively separate the impact component from the vibration signal of hybrid bearing. The STIMD method integrates the idea of nonlinear matching pursuit, so that it can detect the frequency characteristic component of mixed signal near the initial phase function, so it can still effectively separate various mixed components in the case of high noise. The STIMD method combines the advantages of fast independent component analysis and nonlinear matching pursuit. It can separate the multi-dimensional signal blind source to obtain the component signal generated by each vibration source and analyze the component signal to get the fault characteristics of the rolling bearing vibration signal. By nonlinear modelling of complex multidimensional mixed signals and constructing the eigenmode function dictionary conforming to the characteristics of bearing vibration signals, the spatiotemporal intrinsic mode decomposition method can effectively extract the impact signal components of bearing vibration from the mixed signals. By analyzing the envelope spectrum of the component, the characteristic frequency of the fault can be seen and the fault type can be determined.
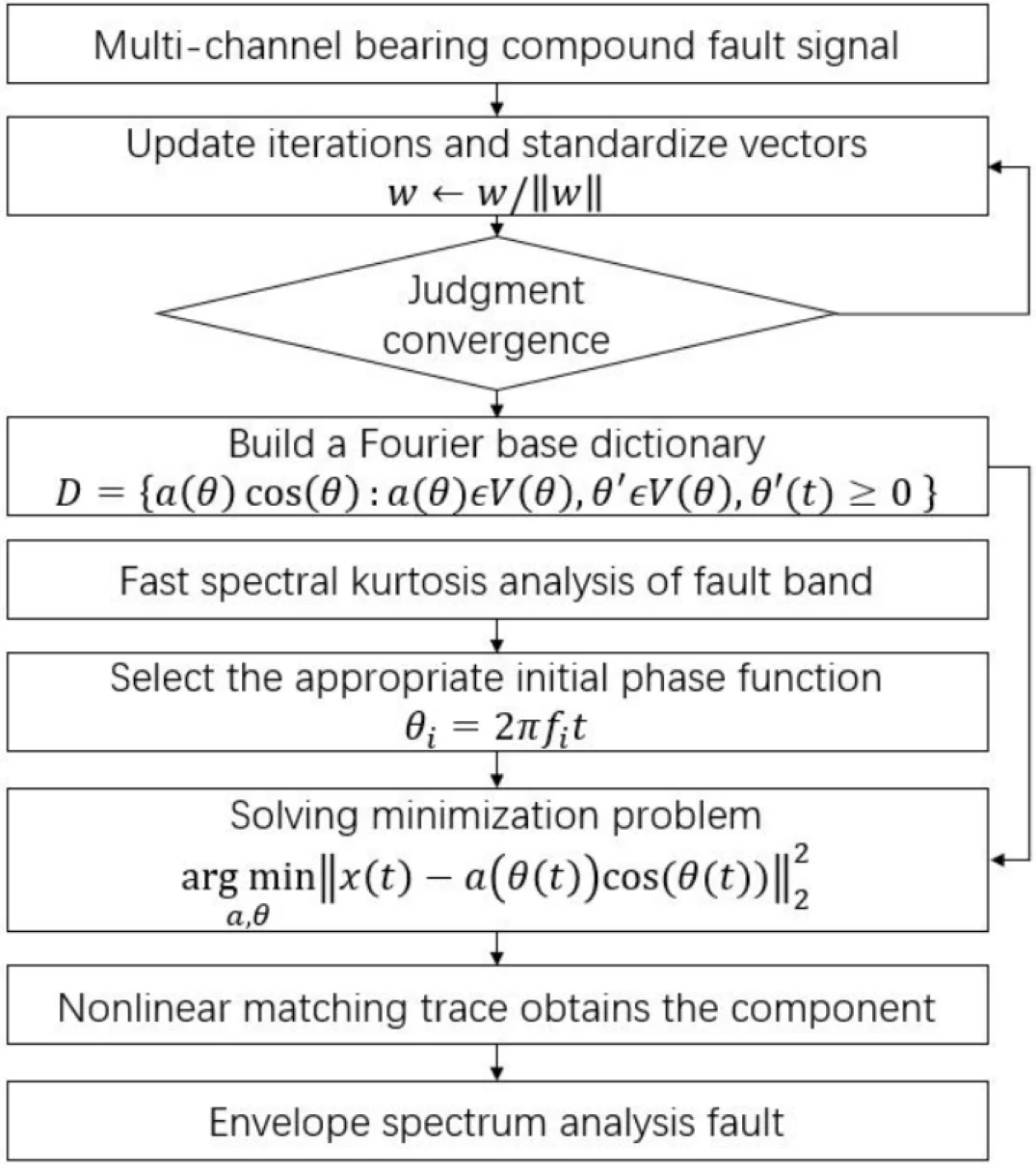
Fig. 1Flow chart of STIMD
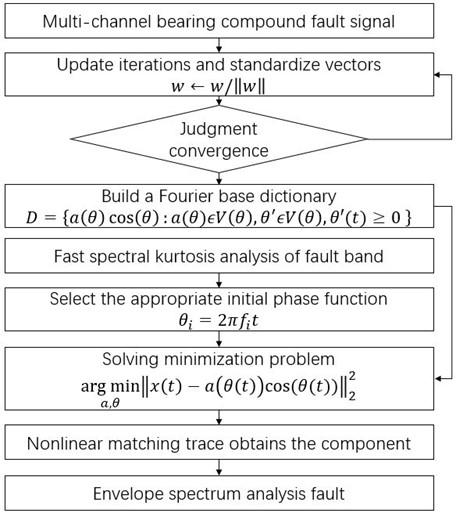
It is particularly important to select the initial phase function of the initial parameter, which can directly affect the accuracy of the solution of the following minimization problem. The selection of the initial phase function can be based on the fault frequency band with high kurtosis found by the fast spectral kurtosis method, and then the center frequency of the fault band can be determined. A suitable initial phase function is selected for nonlinear matching pursuit of the newly formed signal to obtain the source signal component. In the field of actual mechanical fault diagnosis, the initial phase function can be expressed as , is the center frequency determined by the fast spectral kurtosis method. The specific flow chart is shown in Fig. 1.
3. Simulation analysis of bearing compound fault diagnosis
When the rolling bearing inner and outer rings and other local failure, the vibration signal will produce the corresponding impulse signal. The vibration of rolling bearings can be divided into two categories. One is the natural vibration of rolling bearing; The other is the abnormal vibration of rolling bearings, which is related to the surface state of bearings. This section verifies the effectiveness of the spatiotemporal intrinsic mode decomposition method in processing bearing composite fault signals through simulation analysis. The bearing vibration signal monitored in the actual industrial production working environment is bound to be interfered by various factors, such as noise, electromagnetic interference, etc. In practical work, the bearing often generates vibration signals based on modulated signals. Therefore, the vibration simulation signal of bearing compound fault is established as follows:
In the Eq. (17) and Eq. (18), and represent the periodic fault impact signals of the inner and outer rings, respectively. The amplitude 0.5, the frequency 30 Hz, the attenuation coefficients 500 and600. The resonant frequencies 4000 Hz and 3000 Hz, the carrier frequencies in the interference harmonic are 70 Hz and 50 Hz, the inner ring fault characteristic frequencies are 150 Hz, and the outer ring fault characteristic frequencies are 60 Hz. The sampling frequency is 8192 Hz, and white noise with a signal-to-noise ratio of –5 dB is introduced. The number of analysis points is 8192. Hybrid matrix . The time domain diagram of simulated signals is shown in Fig. 2. In the Fig. 2, the inner ring fault is represented by blue, the outer ring fault signal is represented by green, and the black signal is the mixed signal after adding noise. In the figure, the impact signal features are completely submerged in the noise, and there is no obvious impact fault in the time-domain signal.
Fast spectral kurtosis analysis is carried out on simulation signals of bearing compound faults, as shown in Fig. 3.
According to the selected area in the red box in Fig. 3, it is concluded that there are impact characteristics in two frequency bands in the simulation signal. The center frequency is extracted, and the initial phase function of the spatiotemporal intrinsic mode decomposition method is selected according to the frequency band, and its decomposition component is obtained, as shown in Fig. 4.
Fig. 2Simulation signal of bearing Compound fault
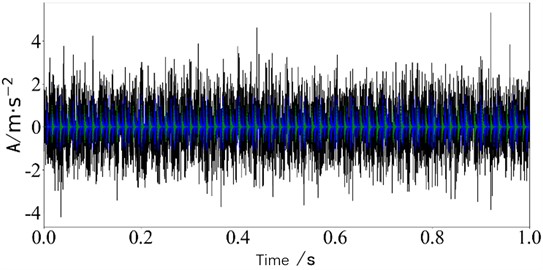
a) Waveform diagram of simulation signal 1
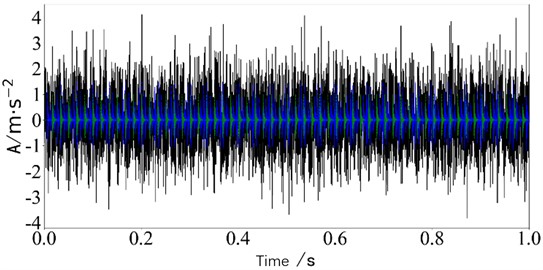
b) Waveform diagram of simulation signal 2
Fig. 3Fast spectral kurtosis diagram of simulation signal
Component 1 approximately represent the inner ring fault component in the rolling bearing compound fault model. Component 2 approximately represent the outer ring fault component in the rolling bearing compound fault model. The fault characteristics of impulse impact exist in time domain diagram. The envelope spectrum analysis of the component obtained by the spatiotemporal intrinsic mode decomposition method was conducted, as shown in Fig. 5. is the inner ring fault frequency, and is the outer ring fault frequency.
Fig. 4Time domain diagram of simulation analysis results of STIMD
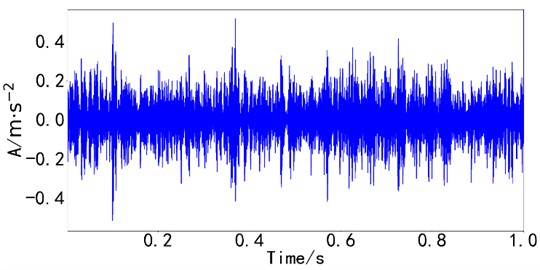
a) Waveform of component 1
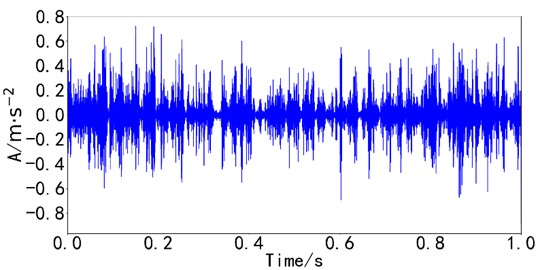
b) Waveform of component 2
Fig. 5Envelope spectrum of simulation results of STIMD
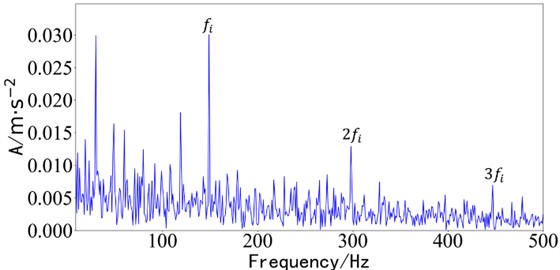
a) Envelope diagram of component 1
b) Envelope diagram of component 2
It can be proved from Fig. 5 that the spatiotemporal intrinsic mode decomposition method can separate the fault frequency of the outer ring and the inner ring as well as the double frequency and triple frequency respectively. The fault frequency is obvious and the fault separation is accurate.
Fast independent component analysis method was used to analyze the vibration simulation signals of the same bearing compound fault. And the waveform diagram of components are shown in Fig. 6.
Fig. 6Time domain diagram of fast ICA
a) Waveform diagram of component 1
b) Waveform diagram of component 2
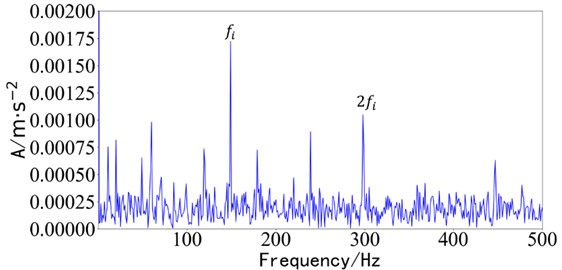
No obvious impact feature exists in the time domain diagram obtained by decomposition. The envelope spectrum of the time-domain component obtained by the fastICA method is analyzed, as shown in Fig. 7. is the inner ring fault frequency.
It can be seen from Fig. 7 that the envelope spectrum of the component obtained by fastICA analysis method can only judge the inner ring fault frequency and its frequency doubling, but cannot extract the outer ring impact frequency, so it cannot effectively separate the compound fault.
By analyzing the simulation signal model of the bearing compound fault, it can be verified that the STIMD method can accurately separate the inner ring fault from the outer ring fault. Selecting the initial phase function by fast spectral kurtosis can solve the minimization problem more quickly. Compared with the fastICA method, the STIMD method can realize the inner and outer ring fault separation in bearing compound fault diagnosis, and embody multiple frequency doubling.
To verify the effect of STIMD under different signal-to-noise ratios (SNR) and to further compare with the fast independent component analysis method. Kurtosis, as an index to measure the impact characteristics of the signal, can reflect whether the fault impact characteristics in the component are obvious to a certain extent. The kurtosis change of the decomposition component is analyzed when the signal-to-noise ratio is from –10 dB to 10 dB. In order to make the trend more obvious, the abrupt value generated by random noise is ignored and the polynomial is used to fit the data, so that the curves of signal-to-noise ratio and kurtosis are smoother and more intuitive. The signal-to-noise ratio and kurtosis curves of the two channels of the simulated signal and the two corresponding components obtained by the decomposition method are shown in Fig. 8.
Fig. 7Component envelope spectra obtained by fastICA
a) Envelope diagram of component 1
b) Envelope diagram of component 2
It can be seen from Fig. 8 that compared with the fastICA method and the STIMD method has a significant improvement in component kurtosis. As shown in Fig. 8, the kurtosis of the STIMD method after fast spectral kurtosis optimization is about 8, while the kurtosis of fastICA and simulation signal is about 3.5. Through numerical comparison, it can be seen that the fault impact component can still be extracted by the STIMD method under the condition of a low signal-to-noise ratio, i.e. the impact characteristics are not obvious. In conclusion, the STIMD method can realize the separation of inner and outer ring faults and diagnose the existing faults under the condition of a low signal-to-noise ratio in the simulation and verification of bearing composite fault simulation signal model.
4. Case analysis of bearing compound fault diagnosis
4.1. Test equipment
In order to further verify the practicability of the proposed method, the vibration signals collected in the actual experiment is analyzed. Relevant experimental research is conducted in Guilin University of Electronic Science and Technology with the help of corresponding author Yanxue Wang in 2021.The MFS-MG mechanical fault comprehensive simulation test bench is used to conduct the test. The test system consists of a driving motor, a speed monitor, an acceleration sensor, a hand regulator, a flexible coupling, a load gearbox and an experimental bearing. The test bench is shown in Fig. 9. ER-12K type rolling bearings were selected for the test bearing, whose dimensions were shown in Table 1. Bearings with compound faults were installed near the driving motor and multi-channel vibration information was collected by piezoelectric acceleration sensors. The signal acquisition position was shown in Fig. 10. The faulty bearing is shown in Fig. 11.
Fig. 8Relationship between SNR and kurtosis
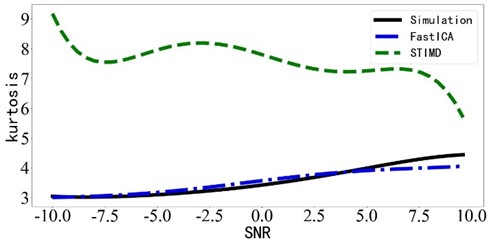
a) Simulation signal 1 and component 1 of the two methods
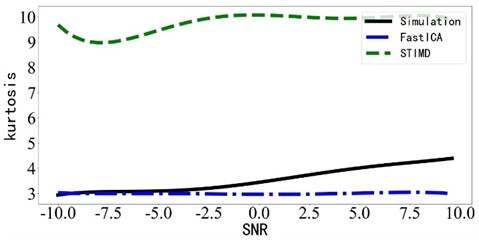
b) Simulation signal 2 and component 2 of the two methods
Fig. 9Bearing fault experiment platform
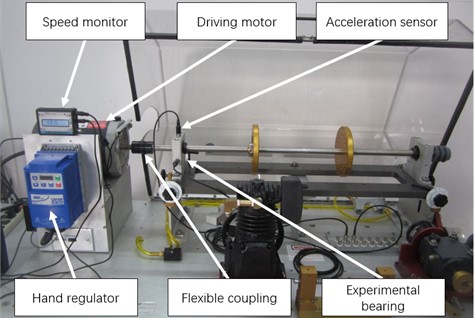
Table 1ER-12K bearing parameters
Outer ring diameter / mm | Inner ring diameter / mm | pitch circle diameter / mm | Number of rollers | Roller diameter / mm | Contact angle / (°) |
52 | 25.4 | 33.4772 | 8 | 7.9375 | 0 |
In the test process, the motor frequency 29.87 Hz, sampling frequency 25.6 kHz, analysis sampling number 25600, that is, analysis sampling time 1s. According to the basic dimension parameters of bearings, the frequency information of motor rotation and Eq. (16) and (17), the inner ring fault frequency is 147.81 Hz, and the outer ring fault frequency is 91.15 Hz:
where, is the number of rolling bodies, and is the diameter of rolling bodies; is the pitch circle diameter and is the contact Angle.
Fig. 10Signal acquisition position of the experiment platform

Fig. 11Compound fault bearing

4.2. Bearing compound fault diagnosis
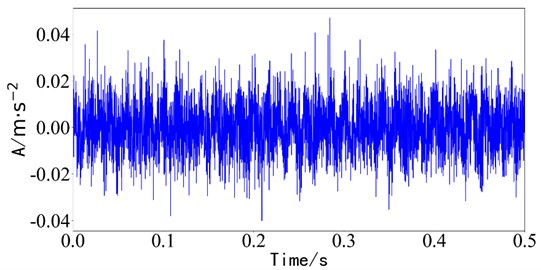
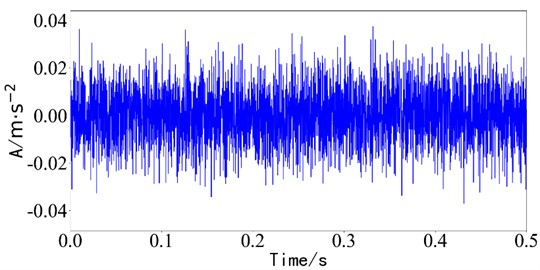
The bearing compound fault collected by the test equipment is a signal containing an inner ring fault and outer ring fault. And the time-domain waveform is shown in Fig. 12.
Fig. 12Time domain diagram of the signal of bearing composite fault
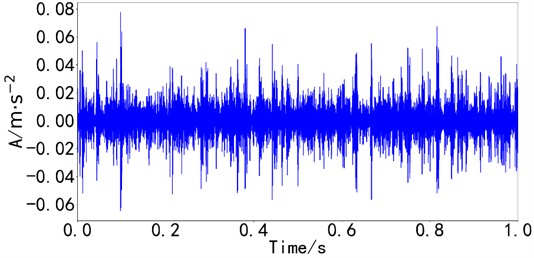
a) Time domain diagram of channel 1
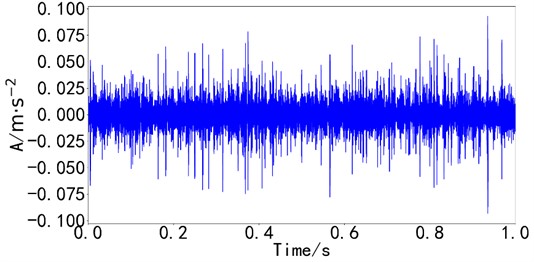
b) Time domain diagram of channel 2
There is no obvious impact characteristic in the time domain vibration signal, and the fault type cannot be judged. Rapid spectral kurtosis analysis is performed on the bearing composite vibration signals collected in the experiment, as shown in Fig. 13.
Fig. 13Fast spectral kurtosis of experimental signal
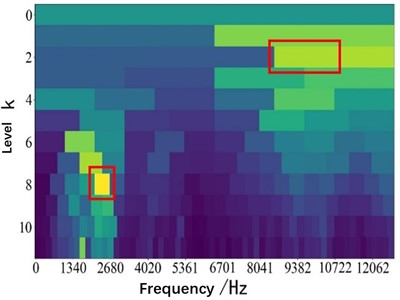
Two fault bands with high energy are obtained by fast spectral kurtosis analysis and then filtered and analyzed by the STIMD method. The result is shown in Fig. 14.
Fig. 14Decomposition result waveforms of STIMD
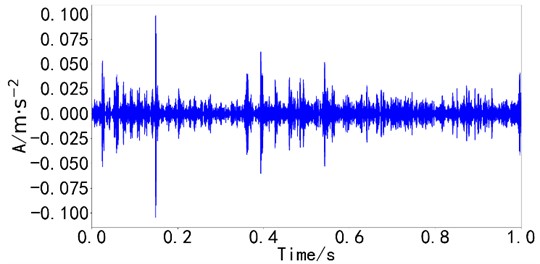
a) Waveform diagram of outer ring fault component
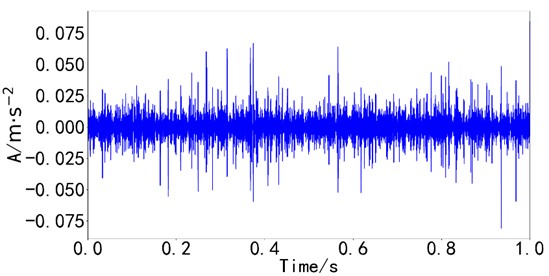
b) Waveform of inner ring fault component
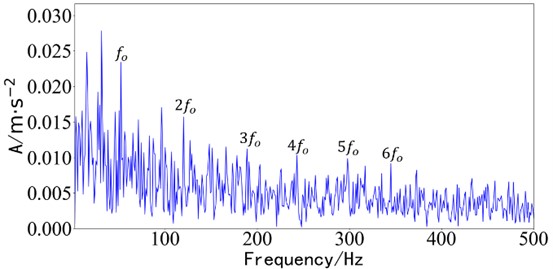
It is not difficult to find periodic impact signals in the time domain waveform in Fig. 14. The envelope spectrum analysis of the fault component obtained by the STIMD method is carried out, as shown in Fig. 15. is the inner ring fault frequency, and is the outer ring fault frequency.
Fig. 15Decomposing component envelope diagram of STIMD
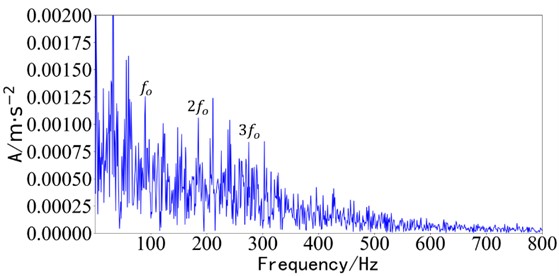
a) Envelope diagram of outer ring fault component
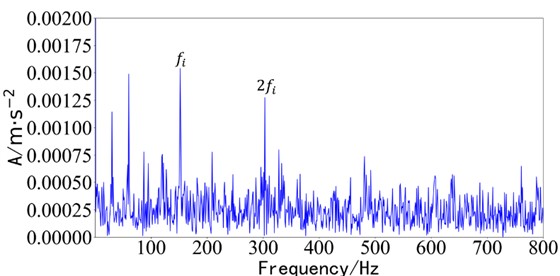
b) Inner ring fault component envelope diagram
The existence of inner and outer ring faults can be determined from the envelope spectrum of components, and the effective separation and extraction of fault types can be realized. From Fig. 15(a), the outer ring failure frequency with a large value can be analyzed; from Fig. 15(b), the inner ring failure frequency and its double frequency can be analyzed. It is shown that the inner and outer ring faults can be decomposed and separated from the multi-channel bearing vibration signals by the STIMD method which selects the initial phase function by fast spectral kurtosis optimization, and the bearing compound fault diagnosis can be realized.
When the same test data is used to analyze the bearing vibration compound fault signals through the fast ICA method, the result is shown in Fig. 16.
The time domain signal component does not have an obvious impact component. The envelope analysis is carried out on the time domain component decomposed by the fast ICA method, and the envelope spectrum as shown in Fig. 17 is obtained. is the inner ring fault frequency.
Fig. 16Time domain diagram of fast ICA
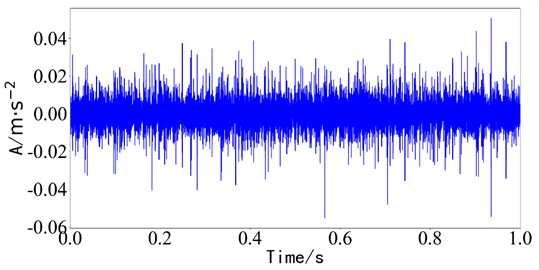
a) Waveform diagram of component 1
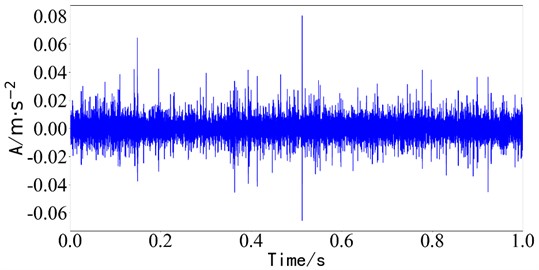
b) Waveform diagram of component 2
Fig. 17Envelope spectrum of results of fast ICA
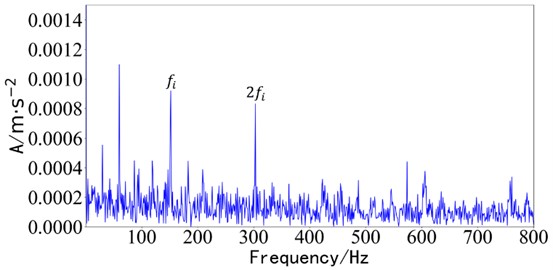
a) Envelope spectrum of component 1
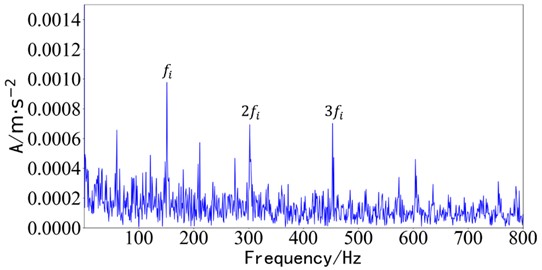
b) Envelope spectrum of component 2
In the envelope spectrum of fast independent component analysis, only the inner circle fault can be detected, but the outer circle fault cannot be distinguished. Therefore, the composite bearing fault diagnosis method applied in the test cannot realize the separation and judgment of the fault frequency of the inner ring and the outer ring.
In conclusion, the spatiotemporal intrinsic mode decomposition method selects the key parameter of the initial phase function through fast spectral kurtosis optimization, which can effectively solve the problem that the fast independent component analysis method cannot effectively judge and separate the inner and outer ring faults in bearing compound fault diagnosis.
5. Conclusions
Aiming at the problem that it is difficult to separate multiple fault characteristic components from multi-channel composite fault signals of rolling bearings, a composite fault diagnosis method of rolling bearings based on spatiotemporal intrinsic mode decomposition method combined with fast spectral kurtosis was proposed. High kurtosis frequency band in vibration signal is determined by fast spectral kurtosis, and the center frequency of frequency band is selected as the basis of initial phase function selection. The simulation signal model was established according to the composite fault signal characteristics of the rolling bearing. The signal model contained two impact components and the signal-to-noise ratio was –5, which completely covered the impact characteristics. In addition, the kurtosis index of the proposed method is higher than that of the contrast method and mixed signal under different signal-to-noise ratio. In this paper, the compound faults of the inner and outer rings of experimental rolling bearings are analyzed. By comparing nonlinear with the comparison method, it is shown that the method can effectively separate the two fault characteristic components and reflect the impact characteristics more comprehensively, which proves that the spatiotemporal intrinsic mode decomposition method with fast spectral kurtosis optimization can realize the compound fault diagnosis of rolling bearings.
References
-
Huang et al., “Automatic quantitative diagnosis for rolling bearing compound faults via adapted dictionary free orthogonal matching pursuit,” Measurement, Vol. 154, 2020, https://doi.org/10.1016/j.measurement.2020.10747
-
S. P. Parida and P. C. Jena, “Free and forced vibration analysis of flyash/graphene filled laminated composite plates using higher order shear deformation theory,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 236, No. 9, pp. 4648–4659, May 2022, https://doi.org/10.1177/09544062211053181
-
S. P. Parida, P. C. Jena, and R. R. Dash, “Dynamics of rectangular laminated composite plates with selective layer-wise fillering rested on elastic foundation using higher-order layer-wise theory,” Journal of Vibration and Control, p. 107754632211383, Nov. 2022, https://doi.org/10.1177/10775463221138353
-
S. P. Parida and P. C. Jena, “Advances of the shear deformation theory for analyzing the dynamics of laminated composite plates: an overview,” Mechanics of Composite Materials, Vol. 56, No. 4, pp. 455–484, Sep. 2020, https://doi.org/10.1007/s11029-020-09896-0
-
Y. Xiao and H. Wang, “A two-step blind source extraction method and its application in fault diagnosis of rolling element bearing,” Journal of Mechanical Science and Technology, Vol. 33, No. 3, pp. 1141–1148, Mar. 2019, https://doi.org/10.1007/s12206-019-0212-6
-
X. Zhao, Y. Qin, C. He, and L. Jia, “Underdetermined blind source extraction of early vehicle bearing faults based on EMD and kernelized correlation maximization,” Journal of Intelligent Manufacturing, Vol. 33, No. 1, pp. 185–201, Jan. 2022, https://doi.org/10.1007/s10845-020-01655-1
-
L. Feng, Y. Zhang, X. Li, and Y. Fu, “Independent component analysis based on data-driven reconstruction of multi-fault diagnosis,” Journal of Chemometrics, Vol. 31, No. 12, p. e2932, Dec. 2017, https://doi.org/10.1002/cem.2932
-
L. Wei et al., “A novel partial discharge ultra-high frequency signal de-noising method based on a single-channel blind source separation algorithm,” Energies, Vol. 11, No. 3, p. 509, Feb. 2018, https://doi.org/10.3390/en11030509
-
H. Li, T. Liu, X. Wu, and Q. Chen, “A bearing fault diagnosis method based on enhanced singular value decomposition,” IEEE Transactions on Industrial Informatics, Vol. 17, No. 5, pp. 3220–3230, May 2021, https://doi.org/10.1109/tii.2020.3001376
-
Y.-K. Gu, X.-Q. Zhou, D.-P. Yu, and Y.-J. Shen, “Fault diagnosis method of rolling bearing using principal component analysis and support vector machine,” Journal of Mechanical Science and Technology, Vol. 32, No. 11, pp. 5079–5088, Nov. 2018, https://doi.org/10.1007/s12206-018-1004-0
-
C. Hu, Y. Wang, and T. Bai, “A tensor-based approach for identification of multi-channel bearing compound faults,” IEEE Access, Vol. 1, No. 7, pp. 38213–38223, 2019, https://doi.org/0.1109/access.2019.2906784
-
F. Miao and R. Zhao, “A new fault diagnosis method for rotating machinery based on SCA-FastICA,” Mathematical Problems in Engineering, Vol. 2020, pp. 1–12, Apr. 2020, https://doi.org/10.1155/2020/6576915
-
L. S. Pinto et al., “Compression method of power quality disturbances based on independent component analysis and fast Fourier transform,” Electric Power Systems Research, Vol. 187, p. 106428, Oct. 2020, https://doi.org/10.1016/j.epsr.2020.106428
-
T. Y. Hou and Z. Shi, “Data-driven time-frequency analysis,” Applied and Computational Harmonic Analysis, Vol. 35, No. 2, pp. 284–308, Sep. 2013, https://doi.org/10.1016/j.acha.2012.10.001
-
S. M. Hirsh, B. W. Brunton, and J. N. Kutz, “Data-driven spatiotemporal modal decomposition for time frequency analysis,” Applied and Computational Harmonic Analysis, Vol. 49, No. 3, pp. 771–790, Nov. 2020, https://doi.org/10.1016/j.acha.2020.06.005
-
J. Zhao, Y. Zhang, and Q. Chen, “Rolling bearing fault feature extraction based on adaptive tunable q-factor wavelet transform and spectral kurtosis,” Shock and Vibration, Vol. 2020, pp. 1–19, Jul. 2020, https://doi.org/10.1155/2020/8875179
-
S. Wan, X. Zhang, and L. Dou, “Compound fault diagnosis of bearings using improved fast spectral kurtosis with VMD,” Journal of Mechanical Science and Technology, Vol. 32, No. 11, pp. 5189–5199, Nov. 2018, https://doi.org/10.1007/s12206-018-1017-8
-
Y. Hu, W. Bao, X. Tu, F. Li, and K. Li, “An adaptive spectral kurtosis method and its application to fault detection of rolling element bearings,” IEEE Transactions on Instrumentation and Measurement, Vol. 69, No. 3, pp. 739–750, Mar. 2020, https://doi.org/10.1109/tim.2019.2905022
-
H. Ding, Y. Wang, Z. Yang, and O. Pfeiffer, “Nonlinear blind source separation and fault feature extraction method for mining machine diagnosis,” Applied Sciences, Vol. 9, No. 9, p. 1852, May 2019, https://doi.org/10.3390/app9091852
-
W. Deng, Z. Li, X. Li, H. Chen, and H. Zhao, “Compound fault diagnosis using optimized MCKD and Sparse Representation for Rolling Bearings,” IEEE Transactions on Instrumentation and Measurement, Vol. 71, pp. 1–9, 2022, https://doi.org/10.1109/tim.2022.3159005
-
G. A. Brosamler, “An almost everywhere central limit theorem,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 104, No. 3, pp. 561–574, Nov. 1988, https://doi.org/10.1017/s0305004100065750
-
C. Daraio, L. Simar, and P. W. Wilson, “Central limit theorems for conditional efficiency measures and tests of the ‘separability’ condition in non‐parametric, two‐stage models of production,” The Econometrics Journal, Vol. 21, No. 2, pp. 170–191, Jun. 2018, https://doi.org/10.1111/ectj.12103
-
T. Wang et al., “An adaptive confidence limit for periodic non-steady conditions fault detection,” Mechanical Systems and Signal Processing, Vol. 72-73, pp. 328–345, May 2016, https://doi.org/10.1016/j.ymssp.2015.10.015
-
H. Sun, L. Fang, and F. Zhao, “A fault feature extraction method for single-channel signal of rotary machinery based on VMD and KICA,” Journal of Vibroengineering, Vol. 21, No. 2, pp. 370–383, Mar. 2019, https://doi.org/10.21595/jve.2018.20073
-
J. E. Garcia-Bracamonte, J. M. Ramirez-Cortes, J. de Jesus Rangel-Magdaleno, P. Gomez-Gil, H. Peregrina-Barreto, and V. Alarcon-Aquino, “An approach on MCSA-based fault detection using independent component analysis and neural networks,” IEEE Transactions on Instrumentation and Measurement, Vol. 68, No. 5, pp. 1353–1361, May 2019, https://doi.org/10.1109/tim.2019.2900143
-
A. Hyvarinen, “Fast and robust fixed-point algorithms for independent component analysis,” IEEE Transactions on Neural Networks, Vol. 10, No. 3, pp. 626–634, May 1999, https://doi.org/10.1109/72.761722
-
S. Jiang, P. Lin, Y. Chen, C. Tian, and Y. Li, “Mixed-signal extraction and recognition of wind turbine blade multiple-area damage based on improved Fast-ICA,” Optik, Vol. 179, pp. 1152–1159, Feb. 2019, https://doi.org/10.1016/j.ijleo.2018.10.137
-
Y. Wang, J. Xiang, R. Markert, and M. Liang, “Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications,” Mechanical Systems and Signal Processing, Vol. 66-67, pp. 679–698, Jan. 2016, https://doi.org/10.1016/j.ymssp.2015.04.039
About this article
This work was supported in part by the National Natural Science Foundation of China under Grant 51875032, in part by Beijing Talents Project and in part by Fundamental Research Funds for Beijing University of Civil Engineering and Architecture (X20159), in part by Research Project of Young Teachers’ Research Ability Improvement Plan of Beijing University of Civil Engineering and Architecture(X21053), in part by Ministry of Science and Technology-National Key R&D Program of the 13th Five-Year Plan - National Key R&D Program(2021YFF0306303).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Zhixing Li: conception of the study. Yuanxiu Zhang: analysis and manuscript preparation, performed the data analyses and wrote the manuscript. Yanxue Wang: perform the analysis with constructive discussions.
The authors declare that they have no conflict of interest.
