Vehicle steering wheel angle identification research based on dynamic program method

1. Introduction

In modern engineering, the vehicle active safety has received more and more attention. An important inverse problem of the vehicle handling dynamics problem which is anti-obtaining vehicle steering wheel angle input from motion response of the vehicle’s state has gradually been attention, which belong load identification problem.

Vehicle steering wheel angle recognition which can obtain the steering wheel angle of drivers under the known vehicle state response belongs to load identification problem [1]. Vehicle steering wheel angle recognition has a certain guiding role for the drivers to drive the actual process and also provides a theoretical basis for automatic steering vehicle. Scholars from various countries did some theoretical research on vehicle steering wheel angle recognition. They studied vehicle steering wheel angle identification problems systematically by using inverse method and optimized the vehicle steering stability [2-5]. Zhao Youqun group team have done a deep research based on vehicle wheel angle identification of vehicle handling inverse dynamics [6-8]. In recent years, many new methods of load identification emerge with the improvement of computer level. The methods can solve the problem which the conventional load identification methods cannot solve.

This paper presents a dynamic load identification research based on dynamic programming method for the actual road vehicle. Different vehicles steering wheel angle under a given avoidance path tracking are identified by using dynamic programming principle.

2. 3-DOF vehicle dynamic model

In this paper, automotive linear three degrees of freedom angle input model including roll degree of freedom is used. Vehicle sports state coordinates are shown in Fig. 1. Fig. 1(a) is the top view of vehicle motion, and Fig. 1(b) is the rear view of vehicle motion.

Vehicle motion state response is represented by three generalized coordinates: yaw angle $\psi$, sideslip angle $\beta$, car body side angle $\mathrm{\Phi }$. Let automobile state vector $X=\left\{{\omega }_r,\beta ,p,\mathrm{\Phi }\right\}$$T$, ${\omega }_r$ is the yaw rate, $p$ is the roll angular speed. ${\delta }_{sw}$ is the steering wheel angle, the front wheel angle $\delta ={\delta }_{sw}/i$, $i$ is the steering gear ratio. The state equation of the car is obtained by the force balance equation:

where:

The parameters in Eq. (1) are defined in [6].

Fig. 1Vehicle sports state coordinates graph

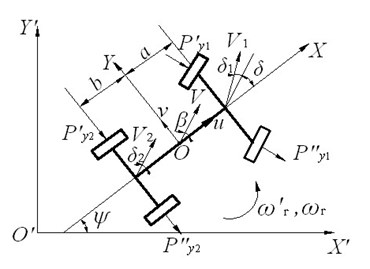
a)

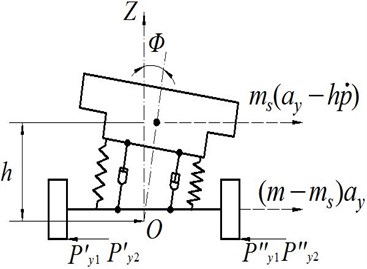
b)

3. Dynamic program algorithm theory

The whole optimization problem is discretized into several sections by the dynamic program algorithm, where each segment has a decision to this functional extremum problem into a multistage decision making process. In a multistage decision making process, when the previous paragraph is used as the initial stage of this paragraph. The optimal decision for the purposes of this paragraph is still an optimal multistage decision. So, a multistage decision problem can be simplified as a single stage of the optimal decision problem, and has nothing to do with before any decision at the corresponding level. Dynamic program algorithm is a very effective tool to solve the multistage decision problem [9-11].

Discrete optimal control problem is formulated as (continuous system can be regarded as unlimited multistage decision making process):

Assuming that the present and future state of the past do not affect the decision making, decision making and goal, it referred to the objective function with Markov property, $u\left(k\right)=u\left(x\right(k),k)$ is either directly measured or reconstructed, $u\left(k\right)$ may be made immediately after getting $x\left(k\right)$:

Eq. (4) indicates the total target for the minimum from the paragraph $\mathrm{k}$ to the last paragraph, and calculate the decision sequence $u\left(k\right),\dots ,u(N-1)$. Then the recursive relationship can be obtained, it is:

4. Analysis of dynamic program algorithm

Taking a vehicle as an example in the identification research based on dynamic program method. The vehicle parameters are as follows: the quality of vehicle $M$ is 1818.2 kg, the quality of suspension $M_s$ is 1418 kg, the distance a from the center of mass to the front axle is 1.463 m, the distance $b$ from the center of mass to the rear axle is 1.585 m, the moment of inertia $I_Z$ of vehicle around the $z$-axis is 3885 kg·m², the moment of inertia $I_Z$ of suspension around the $x$-axis is 980 kg·m², the moment of inertia $I_{XZ}$ of suspension around the $x$-axis and the $z$-axis is 0, the cornering Stiffness (2$k_f$) $k_f$ of the former wheel is 62618 N/rad, the cornering Stiffness (2$k_r$) $k_r$ of the former wheel is 110185 N/rad, the roll angle damping $D_f$ of the former suspension is 3430 N·m·s/rad, the roll angle damping $D_r$ of the rear suspension is 3430 N·m·s/rad, the roll arm $h$ is 0.488 m, the roll angle stiffness $C_f$ of the former suspension is 100548 N·m/rad, the roll angle stiffness $C_r$ of the rear suspension is 32732 N·m/rad, the steering gear ratio $i$ is 24.9, the acceleration of gravity g is 9.8 m·s^-2, the follow order $\alpha$ is 0.5 [12].

To simulate vehicle emergency avoidance under high speed, the avoidance path is double lane (twice avoidance).

The vehicle drives at a high speed of 108 km/h. The yaw angel velocity, lateral acceleration and vehicle body rolling angel of the vehicle mass center obtained by solving the vehicle dynamics model are used as the input of dynamic programming methods, the steering wheel angle and the steering wheel angle speed are used as the output of the dynamic program method. The results are used to be compared with the simulated values to verify the accuracy of recognition dynamic program methods.

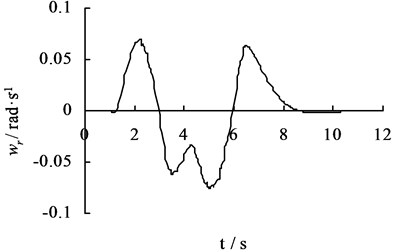
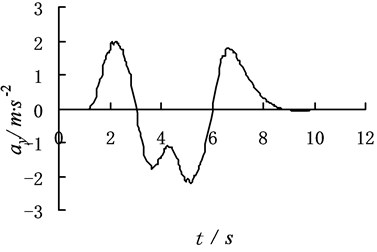
The yaw angel velocity, lateral acceleration and vehicle body rolling angel of the vehicle mass center are got by positive solutions for a new set of pilot model parameters in Fig. 2.

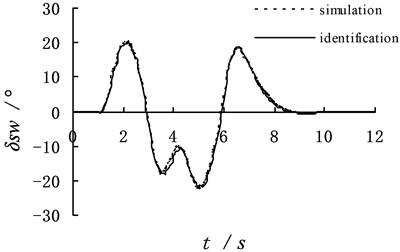
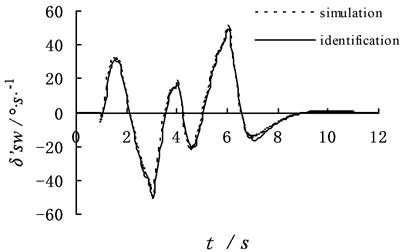
Fig. 3 is the simulation results which identify vehicle steering wheel angle and angular velocity at high speed under the double line avoidance way with the dynamic program method. Dynamic program method can well identify vehicle steering wheel angle and angular velocity in the figure. The identification values are set as ${\delta }_i$ and ${\delta }_i^{\text{'}}$. The simulation values are set as ${\delta }_m$ and ${\delta }_m^{\text{'}}$. The error comparing the identification value with the simulation value is small.

To test the fault tolerance and robustness of the dynamic programming method, the chosen yaw angel velocity, lateral acceleration and vehicle body roll angle are added the maximum amplitude of 10 % uniformly distributed random noise, as shown in Fig. 4.

The yaw angular velocity, lateral acceleration and body rolling angle after adding noise interference are put into the dynamic program method. The identification results of dynamic program method are shown in Fig. 5.

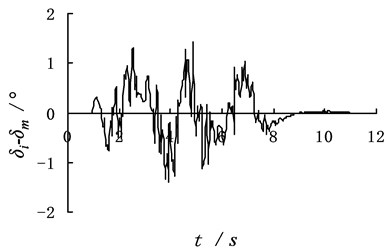
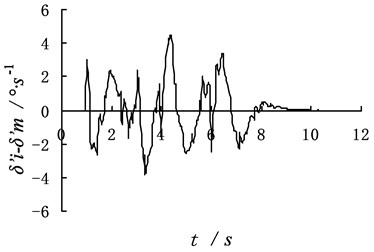
Simulation results show that the absolute error of the identification steering wheel angle and angular velocity changes little. It indicates that the dynamic program method has strong anti-interference capacity. By comparing Fig. 3 with Fig. 5, it is easy to see, the error value of identification between no additive noise and with the additive noise is in a range, which further demonstrates the dynamic program method has strong anti-interference capacity and the accuracy of their identification.

Fig. 2The sample of the input dynamic program method

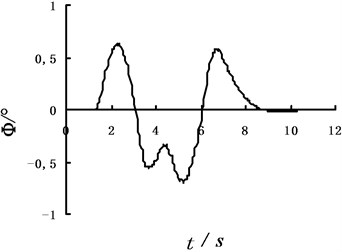
c) The body rolling angle response

Fig. 3The identification result of dynamic program

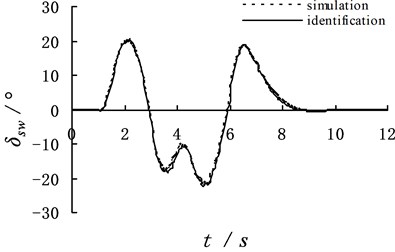
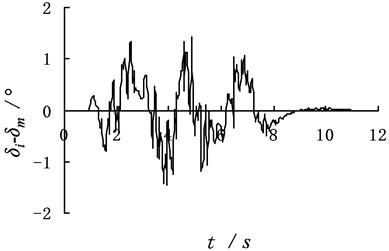
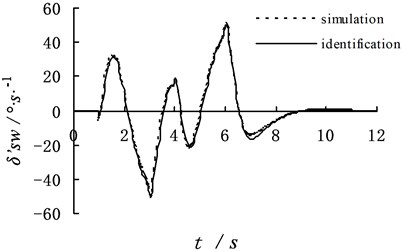
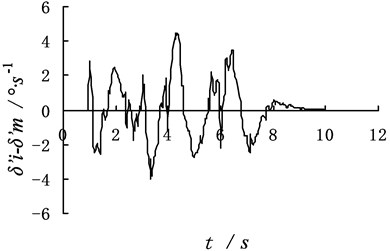
Fig. 4A dynamic programming method input sample with the additive noise

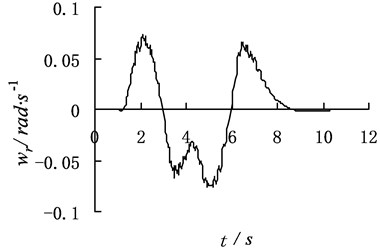
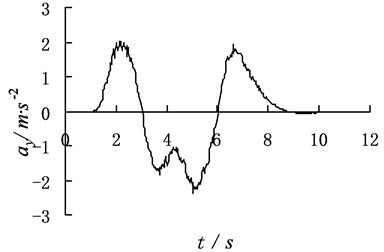
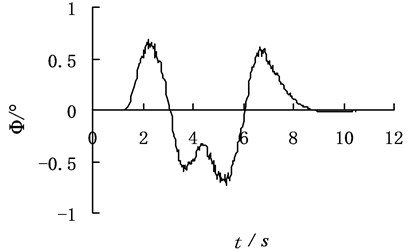
Fig. 5The identification result of dynamic program with the additive noise

5. Conclusions

Through dynamic load identification method based on dynamic program equation, vehicle can be good at tracking the desired avoidance path and identifying the steering wheel angle under the tracking avoidance path by using the dynamic program method and the known vehicle models at high speed. The yaw angel velocity, lateral acceleration and vehicle body rolling angle are added the maximum amplitude of 10 % uniformly distributed random noise. The result indicates that the dynamic program method for steering angle recognition problems with noise is adaptable, and it has a high recognition accuracy and good anti-jamming capability. In this paper, the vehicle steering wheel angle was identified by the dynamic program algorithm. The identification research results pave the way for the vehicle steering vibration characteristics. The vehicle steering vibration characteristics will be studied in the future.