Short-term trend prediction of bearing based on SGWT and MLE method

2.1. The second generation wavelet denoising

The second generation wavelet transform, proposed by Wim Sweldens, is a new wavelet construction method using lifting scheme. It can be seen as an alternate implementation of classical discrete wavelet transform. The main feature of the second generation wavelet transform is that it provides an entirely spatial domain interpretation of the transform, as opposed to the traditional frequency domain based constructions [1]. The decomposition stage of SGWT consists of three steps: split, prediction and update.

In the split step, an approximate signal $a_l$ at level $l$ is split into even samples and odd samples:

In the prediction step, a prediction operator $P$ is designed and applied on $a_{l+1}$ to predict $d_{l+1}$. The resultant prediction error $d_{l+1}$ is regarded as the detail coefficients of $a_l$:

where, $p_r$ are coefficients of $P$ and $M$ is the length of $p_r$.

In the update step, a designed update operator $U$ is applied on $d_{l+1}$. Adding the result to the even samples, the resultant $a_{l+1}$ is regarded as the approximate coefficients of $a_l$:

where, $u_j$ are coefficients of $U$ and $N$ is the length of $u_j$.

Iteration of the above three steps on the output $a$, and then the detail and approximation coefficients at different levels are generated. The reconstruction stage of SGWT is a reverse procedure of the decomposition stage, which includes inverse update step, inverse prediction step and merging step:

The operators $P$ and $U$ are built by means of interpolating subdivision method (ISM) [7]. Choosing different $P$ and $U$ is equivalent to choosing different biorthogonal wavelet filters [8]. The computational costs of the forward and inverse transform are exactly the same.

Then, we can take a simulated signal for example to show the denoising efficiency of the second generation wavelet denoising method as shown in Fig. 1. The signal (frequency 1 Hz amplitude $F_1=$0.05) shown on Fig. 1(a) is corrupted with white noise shown on Fig. 1(b) (SNR = –45 dB), and then the denoising effect of the first and the second generation wavelet denoising were shown on Fig. 1 (c) and Fig. 1 (d).

Fig. 1The comparison between the first and the second generation wavelet denoising

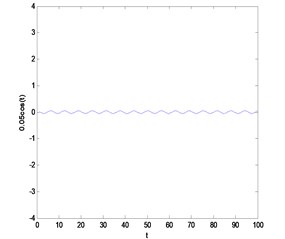
a)

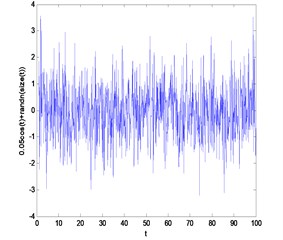
b)

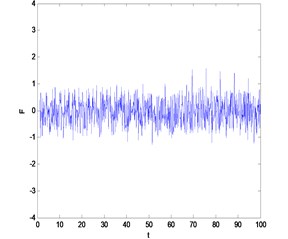
c)

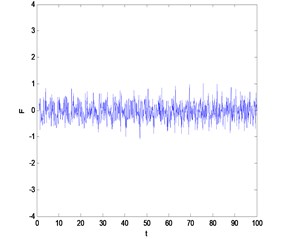
d)

2.2. The improved chaotic time series prediction model based on the maximum Lyapunov exponent

As the chaotic time series conceal the dynamic information of chaotic system and the phase space reconstruction method can reveal the dynamic information, we can reconstruct the chaotic oscillator which depicts the trajectory of the chaotic system [9]. Let $\left\{x\left(t\right)|t=\mathrm{1,2},\dots ,N\right\}$ be the observed time series, according to Packard [10] and Taken [11], based on the selected embedded dimension $m$ and the time delay $\tau$, we can reconstruct the phase space as follows:

where, $i=$1, 2,…, $M$ and $M=N-\left(m-1\right)\tau$.

According to Taken theorem [11], the embedded dimension $m$ and the time delay $\tau$ are the basic parameters of the constructed phase space. Taken assumes that we have an infinite noise-free data set, in which case, we can arbitrarily choose the time delay $\tau$. However, as real data sets are finite and noisy, the choice of the time delay plays an important role in the reconstruction of the oscillator from the scalar time series. If $\tau$ is too small, the reconstructed oscillator is compressed along the identity line which is called redundancy. If $\tau$ is too large, the attractor dynamics may become causally disconnected which is called irrelevance. Furthermore, the Lyapunov exponent is sensitive to the time delay $\tau$ and embed dimension m, the C-C method is used to calculate both the time delay $\tau$ and embed dimension m simultaneously which is more accurately than calculate the two items separately. Rosenstein et al. [12] put forward to the small data set method to calculate the largest Lyapunov exponent. This method can make fully used of the usable data, besides it has the advantage of fast operation and easily implement.

Let $x_i$ be the point in the original phase space, the maximum Lyapunov exponent is ${\lambda }_1$, the delayed time is $\tau$, the embedded dimension is $m$. Then, we can get the point in the reconstructed phase space:

The following equation will be obtained by the maximum Lyapunov exponent ${\lambda }_1$, then:

where, $‖·‖$ denotes the Euclidean norm, $X_k$ is the nearest neighbourhood point of $X_M$, $X_{M+1}$ is the prediction point.

Then, we can take a typical chaotic signal Lorenz for example to show the efficiency of the improved chaotic time series prediction model based on the maximum Lyapunov exponent as shown in Fig. 2. The phase trajectory of Lorenz system is shown in Fig. 2(a), and the time series curve of the variable y in the Lorenz system is shown in Fig. 2(b). Then, the maximum Lyapunov Exponent ${\lambda }_1$ obtained by small data method can be calculated by using least square method of the labeled scale less line as shown in Fig. 2(c), and the comparison between the real data and the forecasting result is shown in Fig. 2(d).

Fig. 2The comparison between the real data and the forecasting result

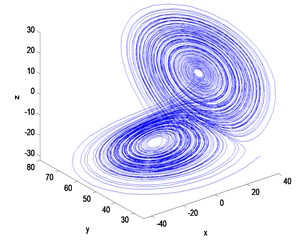
a)

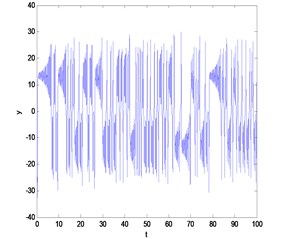
b)

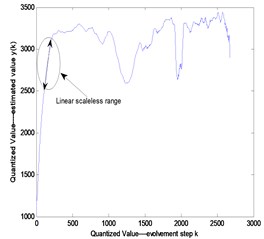
c)

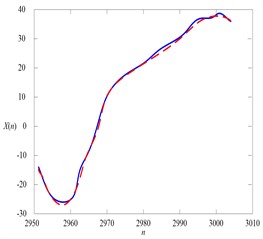
d)

3.1. Experimental setup and data acquisition

A mechanical test bed in the RCM laboratory of Mechanical Engineering College is used in this research to validate the effectiveness of the proposed method in this paper. The test bearing (6220E) is driven by a 15 KW three phase asynchronous drive motor. In addition, the speed and torque sensors are used to acquire the speed and torque information. These components are connected by couplings, as shown in Fig. 2. The sampling frequency of this experimental system is 20 kHz.

Fig. 3The test rig

3.2. Results analysis and discussion

The vibration signal acquired from the test rig is utilized to analyzing according to the method proposed in Section 2. Fig. 4(a) is the original signal without SGWT, and the maximum Lyapunov exponent ${\lambda }_1$ obtained by small data method can be calculated by using least square method of the labeled scale less line as shown in Fig. 4(b). Fig. 5(a) is the original signal with SGWT, and the maximum Lyapunov exponent ${\lambda }_1$ obtained by small data method can be calculated by using least square method of the labeled scale less line as shown in Fig. 5(b).

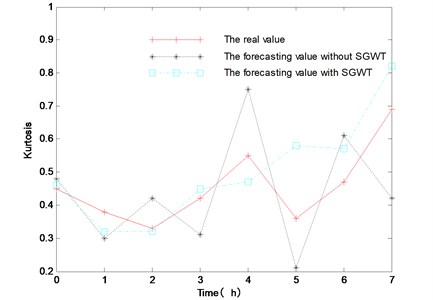
In order to validate the effectiveness of method proposed in this paper, a method based on the second generation wavelet denoising and the maximum Lyapunov exponent is utilized. It can be seen from Fig. 6 that the proposed method can predict the short-term trend of the bearing. So, the effectiveness of the method can be validated.

Fig. 4The original signal without SGWT

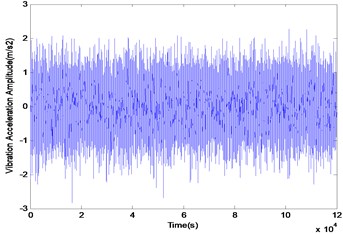
a)

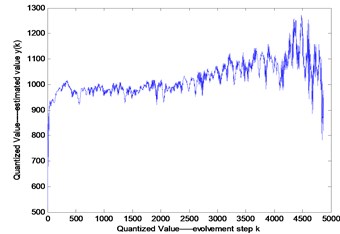
b)

Fig. 5The original signal with SGWT

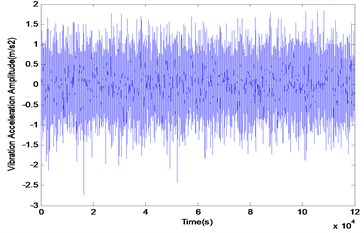
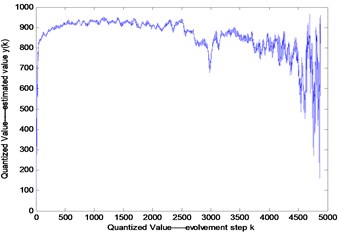
Fig. 6The prediction results of two forecasting methods