Abstract
A rolling element bearing is a common component in household and industrial machines. Even a minor fault in this section has a negative impact on the machinery's overall operation. As a result, the industry suffers significant financial losses, and this damage can potentially result in catastrophic failures. Therefore, even a little fault in the rolling element bearings must be recognized and remedied as soon as possible. Many ways for detecting REB defects have been created in recent years, and new methods are being introduced on a daily basis. This article will provide a summary of such methods, with a focus on vibration analysis techniques. The newest advancements in this field will be recognizable to readers of this article. Anyone interested in defect diagnostics of rolling element bearings can utilize this material.
Highlights
- A rolling element bearing is a common component in household and industrial machines. Even a minor fault in this section has a negative impact on the machinery's overall operation.
- Therefore, even a little fault in the rolling element bearings must be recognized and remedied as soon as possible. Many ways for detecting REB defects have been created in recent years, and new methods are being introduced on a daily basis.
- This article will provide a summary of such methods, with a focus on vibration analysis and artificial intelligence techniques. The newest advancements in this field will be recognizable to readers of this article. Anyone interested in defect diagnostics of rolling element bearings can utilize this material.
1. Introduction
All industries are becoming smarter as part of the fourth industrial revolution. One of the most significant aspects of these smart industries is Prognostics and Health Management (PHM). PHM is a strategy for monitoring system health that provides comprehensive yet tailored solutions, and it is essentially a three-part summary. First and foremost, detecting the presence of a fault is often known as fault detection. Defect diagnosis, on the other hand, is the process of determining the type of fault and its location. Finally, the prognosis might be defined as an estimate of the component's remaining useful life. PHM aids in the cost-effectiveness of all activities in the industry, as well as the protection of the machinery. It also aids in the efficiency and reliability of an asset [1], [2]. This paper describes the recent advancements in the fault diagnosis of rolling element bearings.
Rolling element bearing (REB) is an inevitable machine element used in rotating machinery. The determination of this machine element is to offer an easy movement or rotation of a shaft and housing while transmitting the power [3]. Rolling element bearings, like any other moving component, are prone to developing faults. Fig. 1 lists the most common bearing defects. A damaged bearing can cause serious problems with the machine's operation and, in the worst-case scenario, catastrophic failure. Early diagnosis of bearing defects and correct severity level assessments is therefore crucial for the machines' smooth operation. Many methods are introduced in recent years to find the faults occurring in the bearings. Some of them are vibration analysis, acoustic emission measurement, temperature measurement, wear debris assessment, motor current signature evaluation, etc. Vibration analysis and acoustic emission measurement, however, are the most extensively employed. As a result, these two methods are chosen to create a summary in rolling element-bearing fault diagnostics. Although such defect diagnostic procedures include several steps, this work focuses on signal processing methods. Even though numerous review papers have been published in this field in the past, new review articles are still needed because new methods are introduced regularly.
In 1999 N. Tandon and A. Choudhury [4] reviewed the techniques used for fault diagnostics of REB, they described the vibration and acoustic measurement techniques and compared those with some recent methods. In 2014 Y. Hassan Ali et al. [5] published a summary article on fault diagnosis (FD) and condition monitoring of REB based on AE analysis with the help of artificial intelligence. Soon afterward two researchers [6] wrote a review article about the signal processing methods for the diagnostics and prognosis of REB, they discussed the important condition monitoring tools and their capabilities in depth. In 2019 a research article [7] summarized the techniques used in FD, fault measurement, and fault modeling of REB.
The objectives of this article are to review the latest developments in fault diagnostics and fault classification of REB, to give a brief idea about vibration analysis and acoustic emission measurement, to compare different signal processing techniques with their pros and cons, and to familiarize the role of artificial intelligence methods in identification and classification of bearing faults. The paper's scope aids anyone interested in REB fault diagnostic approaches in learning about the current state of the art. The data for this literature survey is taken from various research papers published in the leading journals in the last three decades. This paper’s methodology is as follows: A brief theory of the vibration and AE analysis is discussed in Section 2. Various signal processing methods in FD of REBs are discussed in Section 3. Artificial intelligence techniques are described in Section 4. Section 5 contains the summary and discussion; after all, Section 6 is where the findings are discussed.
2. Vibration analysis and acoustic emission measurements
2.1. Vibration analysis (VA)
The motion of a body is represented by vibration, which is fundamentally oscillatory around a mean position and can be periodic or aperiodic. To use vibration monitoring to detect flaws in machines, the machine's vibration must first be recorded, and then the vibration signal must be processed to acquire useful information about the machine’s health. Vibrations should be recorded in close proximity to the bearings that support the rotating shafts. Vibrations at any location should be measured in three mutually perpendicular directions if possible. Vibration monitoring is preferred in the majority of rotating machinery. Because every dynamic machine component manifests itself in the machine's measured vibration response at its characteristic frequencies, this is the case. As a result, for fault diagnosis, signal analysis of the recorded vibrations from the machines provides a significant and simple methodology for detecting flaws in operational machines [8], [9].
Fig. 1Common bearing defects
Fig. 2Steps involved in FD of REB
2.2. Acoustic emission analysis
Acoustic emission (AE) is the spontaneous release of transient elastic stress energy when a material deforms. Waves of 2 MHz or higher are emitted by materials under stress. High-frequency piezoelectric-based AE sensors can detect these waves on a body’s surface. These AE waves might be continuous or in bursts, depending on the level of internal stress. The cause of the interior defect can be discovered using the triangulation approach, which involves placing many AE sensors on the surface of a body and collecting high-speed data on the arrival times of these AE waves. This technique is a non-destructive testing method, and it can be used in a variety of ways, such as health monitoring of structures, machine tools, gears, bearings, assessing tribological and wear behavior, etc. [10]-[12]. The benefits and drawbacks of vibration analysis and AE measurement are given in Table 1.
Table 1Benefits and drawbacks of vibration and AE analysis
Techniques | Benefits | Drawbacks |
Vibration analysis | It is possible to monitor machines in real-time. Many well-developed signal processing techniques are available for use | High possibility to get noise-contaminated data. Difficult to find the proper mounting position for vibration sensors |
Acoustic emission analysis | The time for analysis is minimal. Recognition accuracy is high. It is a nondestructive evaluation | Due to a variety of elements such as environmental circumstances, recording software parameters, and reflected acoustic signals, accurately capturing acoustic signals is extremely difficult |
3. Signal processing
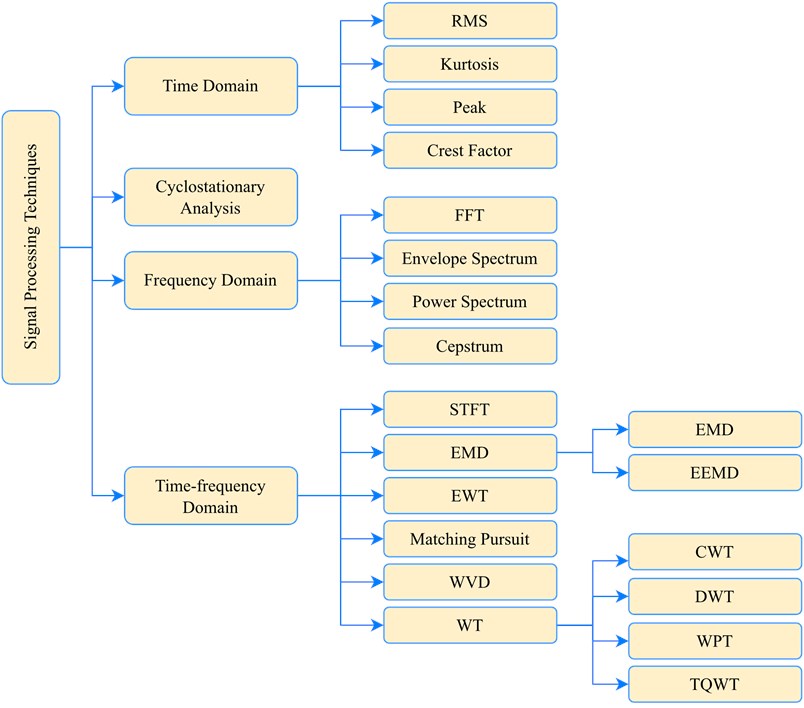
Data acquisition, signal processing, and fault classification are the three pillars of the fault diagnostic procedure in vibration and AE analysis, as given in figure 2. Sensors and analyzers can be used to collect data. The most often used sensors for collecting vibration data include accelerometers, displacement transducers, velocity transducers, and so on. Piezoelectric sensors are used to collect AE signals. These collected data will be transferred to the signal processing unit, which will process the signals further. The data contain all of the relevant information about the bearings' condition. However, the information gathered is a mix of bearing data, information about other functioning elements including gears, shafts, etc., and noise. The signal processing unit may be required in this case. Signal denoising, signal filtering, signal amplification, feature extraction, and fault identification are all examples of signal processing. The signal can be processed in a variety of ways. Some of them are wavelet transform, fast Fourier transform, envelope analysis, root mean square, empirical mode decomposition, matching pursuit, cepstrum, Wigner Ville, etc. [13]. The extraction and selection of features can be conducted particularly in three domain techniques and a cyclo-stationary analysis. The three scales are the time scale, frequency scale, and time-frequency scale. The next sections go through each of these in-depth.
3.1. Time domain techniques
A time-domain analysis is the simplest and most fundamental signal processing technique, which gives the information of a signal concerning the time. In the time domain technique, the typical characteristic features in particular crest factor, kurtosis value, peak value, root mean square value, etc. are investigated to get the idea of fault present in the bearings [14], [15]. The RMS value represents the vibration’s power content. The signal's greatest value over time is called the peak. The crest factor is the representation of the ratio of the input signal's peak value to its RMS value. Kurtosis is a statistical metric that is employed to describe the shape of a signal. In essence, it is a metric for determining the “peakedness” of a random signal. Each feature's benefits and drawbacks are listed in table 2. Some researchers [16], [17] published articles on intelligent diagnosis techniques of REB faults employing time-domain characteristics and artificial neural networks (ANN). The RMS value, kurtosis value, and negative log-likelihood parameters are employed as the inputs for ANN, which are obtained from the processed time-domain signals. The time-domain analysis technique, on the other hand, is ineffective for higher-order systems. Furthermore, employing time-domain analysis to acquire all information concerning the REB’s failure is unfeasible. As a result, we'll look into other options.
3.2. Frequency domain techniques
In the frequency domain, several characteristics which are not detectable in the time domain can be found. The frequency-domain approach plots a signal's information along the frequency axis vs its amplitude. Signal feature extraction and selection employing frequency domain include fast Fourier transform, power spectrum, Cepstrum, and envelope spectrum. This section explains them.
3.2.1. Fast Fourier transform (FFT)
The Fourier transform was put forward by Joseph Fourier, a French physicist and mathematician in the 19th century. He found that “any periodic function can be decomposed in a series of simple oscillating functions, namely sines and cosines”. That means Fourier transform separates a vibration signal in the form of complex exponential functions at dissimilar frequencies [18]. In 2007 two researchers [19] investigated the fault diagnostics of a rolling bearing employing FFT of the Intrinsic Mode Functions (IMF) with the help of Hilbert Huang Transform (HHT). This paper addressed the inefficiency of traditional DFT and the inherent problems of Wavelet Transform (WT) such as lengthy computational time and inappropriate resolution for investigating non-stationary vibration signals coming out of faulty bearings. However, the primary drawback of FFT is that it computes over the entire period so that it is impossible to distinguish the stationary and transient components of the signal easily.
Table 2Benefits and drawbacks of time-domain characteristics
Time-domain characteristics | Benefits | Drawbacks |
RMS | A straightforward technique that is directly tied to the vibration profile's energy content | Only high-amplitude parts are susceptible to changes in RMS vibrations |
Kurtosis | Great sensitivity to shock and high performance in detecting periodic impulses | The kurtosis meter is expensive. |
Peak | Straightforward technique | Noise sensitivity |
Crest Factor | The crest factor meter is a simple to use and inexpensive device | Only in the framework of relevant impulsiveness is it trustworthy |
3.2.2. Envelope analysis
Envelope Analysis (EA) is a renowned technique to collect periodic impacts from a machine’s vibration or AE signal. The envelope analysis technique's primary idea is to use the envelope spectrum to remove the disturbance effect and accentuate the fault feature [20]. Hilbert transform (HT) is one of the most extensively employed techniques in envelope spectrum analysis. It has an outstanding application in the area of fault identification and diagnostics of machine elements. McInerny et al. [21] used EA in 2003 for basic vibration signal processing to detect bearing faults. In 2017 C. Mishra et al. [22] studied the defect diagnostics of REB by the application of envelope analysis as well as wavelet de-noising along with sigmoid function-based thresholding. As per the technique, it was supposed that the vibration signal coming from the defective bearings consists of a specific part indicating a large number of fault features and noise components. For extracting these large-scale features from the vibration signal, a Bayesian estimator was used after processing the wavelet coefficients.
3.2.3. Power spectrum
Power spectral techniques have great applications in the context of fault diagnostics of machinery. According to this technique, it is hard to investigate the phase indication of the signal, which contains severe diagnostic information. So, for conserving the phase information, the collective time-frequency analysis technique is adopted. The power spectrum is frequently selected for health monitoring techniques as it efficiently denotes the time, the variant time-domain vibration signal into a group of defined length vectors indicating the square values of the frequency components [23], [24]. K. F. Al-Raheem et al. in 2007 [25] studied the fault diagnostics of REB based on Laplace-wavelet-envelope Power Spectrum. The authors tried to find out a unique method for identifying the localized defects present in the inner and outer races of the rolling contact bearing through the envelope-power spectrum of the Laplace coefficient. It is clear to observe that the peaks of the power spectrum are very sensitive to the shaft fluctuations, this is considered as a drawback while processing the signal.
3.2.4. Cepstrum
Cepstrum analysis is a nonlinear signal processing procedure that can be used in the detection, classification, and removal of harmonic and sideband families from vibration and AE signals. A study [26] was conducted on the fault diagnostics of automotive ball bearings at the early stages by the application of the Minimum Variance Cepstrum (MVC). The authors presented MVC for the investigation of repeated impulse signals present in noisy circumstances. MVC is accomplished through a logarithmic-power spectrum, it is intended by the least variance procedure. In 2019 D. Ibarra-Zarate et al. [27] proposed a methodology to extract vibration and AE signals from faulty bearings based on the cepstrum pre-whitening technique. They found that the suggested approach can perform well in defect identification of bearings in medium and late stages. Researchers have used the different variance of cepstrum such as MVC and cepstrum pre-whitening for fault diagnosis of machine elements, but it is computationally expensive.
Table 3Different frequency domain techniques with benefits and drawbacks
Frequency domain techniques | Benefits | Drawbacks |
FFT | The technique is simple to use and implement | Unable to examine transient features in a timely manner |
Envelope analysis | Performs well even when there is a minor random fluctuation | This can result in a major diagnosis error |
Power spectrum | Higher spectrum estimation performance than the FFT, which is useful for detecting signals that change considerably over a short period | Due to its intricacy, it necessitates the expertise of professionals. Peaks of the power spectrum are very sensitive to shaft fluctuations |
Cepstrum | Simple to use and useful for sideband analysis | The variations of the spectrum curve are averaged out due to the filtering, and it can only be used for well-separated harmonics. Computationally expensive |
3.3. Cyclo-stationary analysis
A different context is introduced for investigating periodically time-variant signals by cyclo-stationary analysis. It is assumed that the signals are static in traditional stationary signal processing techniques, whereas the cyclo-stationary analysis treats the signal as a periodically time-varying element. Nonstationary signals are considered cyclo-stationary when certain of their characteristics are periodic [28], [29]. P. K. Kankar et al. in 2013 [30] investigated the defect diagnostics of REBs by the combination of cyclic autocorrelation and wavelet transform. The key concept of the paper was developing a feature extraction system with the help of a cyclic autocorrelation of raw vibration signals coming out of the defective bearings. When the non-stationary signals underwent cyclo-stationary analysis, more than a few distinct modulating frequencies were present.
3.4. Time-frequency domain techniques
The time domain and frequency domain analyses were discussed in sections 3.1 and 3.2. The integration of both of these analyses will be discussed in this section. The Time-frequency domain gives the information of signals in both time and frequency scales. A vibration signal consists of many signal components having different characteristics such as linear and non-linear behavior, stationary and non-stationary, etc. So, it is substantial to conduct the time-frequency analysis for extracting the fault characteristic properties and eliminating noise components efficiently [31]. Important time-frequency practices used are short-time Fourier transform, empirical mode decomposition, wavelet transform, empirical wavelet transform, matching pursuit, Wigner-Ville distribution, etc.
Fig. 3List of various signal processing methods used in the FD of REB
3.4.1. Short-time Fourier transform (STFT)
STFT is a basic and straightforward signal transformation technique for converting time-domain signals to time-frequency space. This approach uses a window function to multiply time series in which the non-stationary vibration signal can almost be found to be locally stationary and then convert into the time-frequency domain. To improve the signs of localized fault, spectrograms of STFT are averaged in the time-frequency domain. The phase underlines the energy flow associated with the impacts between defective components of the bearing as well as strengthens the signal-to-noise ratio [32], [33]. In 2015 H. Gao et al. [34] studied the vibration signal feature extraction procedures for fault diagnostics of REBs by the application of STFT plus non-negative matrix factorization (NMF). Researchers adopted a new time-frequency distribution (TFD) matrix-factorization by merging the ideas of TFD with NMF. However, STFT gives a constant time resolution once the window size is fixed. Hence further investigations are required to overcome this drawback in real-time applications.
Table 4Different time-frequency domain techniques with benefits and drawbacks
Time-frequency domain techniques | Benefits | Drawbacks |
STFT | A simple approach, suitable for novices in time-frequency analysis, with low computing complexity | It's challenging to create a quick and efficient technique to compute STFT with constant frequency resolution for the entire signal |
EMD | Self-adaptive decomposition process. Not requiring a preexisting set of mathematical functions | EMD overestimates the number of modes so that there is a chance to occur the mode mixing problem while processing the signal |
EWT | EWT focuses more on the oscillating part It is also faster in terms of computing than EMD | If the input signal consists of two chirps that overlap in both the temporal and frequency domains, the EWT will be unable to distinguish between them |
Matching Pursuit | MP is a materialistic method that finds the best waveform from the signal at each iteration | The dictionary density determines the success of the MP algorithm. Increased density improves efficiency, but it may also result in increased computing time and storage space |
WVD | It has a good frequency and time resolution. Its implementation does not necessitate the use of a window function | The cross-term interference misleadingly indicates the presence of signal components between auto-terms |
WT | Provide better temporal localization at high frequencies than STFT, are more versatile than STFT, and have a wider range of wavelet functions | Choosing the mother wavelet type is challenging |
3.4.2. Empirical mode decomposition (EMD)
EMD is a time-frequency domain self-adaptive decomposition algorithm that may decompose any vibration signal into empirical modes corresponding to the numerous oscillation modes implanted in the signal. Any vibration signal could be generated by the linear superposition of empirical modes, according to the EMD algorithm. EMD is a signal processing approach that can be used to treat non-stationary and non-linear data whose local-time measure is dependent on the signal. It can also decompose the signal into a finite number of IMFs [35], [36]. A study [37] was conducted to review the application of the EMD procedure in FD of rotating machinery in which the authors tried to report the earliest EMD technique alone, advanced EMD, and the combination of EMD with other techniques. In 2015 J. Ben Ali et al. [38] studied automated fault diagnostics of the REB from vibration signals. The key concept of the research was the implementation of the EMD as well as ANN for fault diagnostics and fault classification. A Health Index (HI) was introduced and tested based on the vibration signal of three bearings at different speed and torque conditions. However, EMD overestimates the number of modes so there is a chance to occur the mode mixing problem while processing the signal.
3.4.3. Empirical wavelet transform (EWT)
Vibration signals consist of frequency modulated and amplitude modulated components. EWT is utilized to extract the above-said signal components from vibration signals. EWT could be applied for fault identification as well as the fault classification of the REB [39]. In 2019 S. N. Chegini et al. [40] wrote an article on the de-noising technique for the diagnosis of faulty bearings by the application of a new empirical wavelet transform. The authors divided the paper into two stages; one was the de-noising stage, and the other was the fault diagnosis stage. In the de-noising stage, the EWT method was employed to break down the vibration signal into different empirical modes. In the fault-diagnosis phase, the presence of a fault and its location were identified by applying the envelope spectra and kurtosis number of the de-noised signal.
3.4.4. Matching pursuit
The Matching Pursuit algorithm is able to break down any vibration signal into the linear expansion of waveforms, which is suitable for a dictionary of functions. The above said wave-forms are carefully chosen for the sake of getting the finest match of signal structures. The matching pursuit decomposition provides an interpretation of the signal structures. If a signal structure does not correlate well with any dictionary function, it is sub-decomposed into numerous functions and its information is diluted. Matching pursuit is a materialistic algorithm that selects a waveform at each iteration that would be the best part of the signal [41]. In 2005 H. Yang et al. [42] investigated the fault diagnostics of REB by the application of basis pursuit. This paper explained the vibration signal feature extraction coming out of a defective bearing with inner-race and outer-race defects by using the application of a time-frequency procedure called the Basis Pursuit. The interpretation of the analyzed results was easier in the basis pursuit technique because it denoted the characteristic properties with excellent resolution in the time-frequency domain. However, the success of the MP algorithm depends on the density of the dictionary. If the density increases, the efficiency increases, but it could result in an increase in the computational time and storage space.
3.4.5. Wigner Ville distribution (WVD)
WVD is the time-frequency domain technique coming under Cohen class distribution, which could be employed in the space of fault diagnostics and fault classification of the REBs. The primary advantage of WVD includes better resolution in time and frequency domains. WVD has gained significant consideration in recent years for analyzing non-stationary or periodic signals and it could be used in machine condition monitoring, structure bone noise identification, etc. [43], [44]. In 2011 Y. Zhou et al. [45] studied the Wigner–Ville distribution by virtue of the Cyclic Spectral Density (CSD) to investigate the cyclo-stationary vibration signals coming out of faulty bearings. In this process, the CSD of the cyclo-stationary signals was calculated and WVD was applied through the inverse Fourier transform. One major disadvantage of WVD is cross-term interference. These cross-terms misleadingly indicate the presence of signal components between auto-terms.
3.4.6. Wavelet transform (WT)
Wavelet transform is a major reliable method in the time-frequency domain for defect diagnostics of REBs. In this method, the feature information would be stored in time-frequency domains. The most important step in this technique is to choose a suitable wavelet when investigating the vibration signals coming from the faulty bearings. A wavelet function is a tiny wave that holds oscillating wave-like features and is required for implementing the wavelet transform [46], [47]. In a paper [48], the theory and functions of wavelet transform in defect diagnosis of rotating machines were reviewed. WT has four derivatives: CWT, DWT, WPT, and TQWT, which are explained below.
3.4.6.1. Continuous wavelet transform (CWT)
Wavelet coefficients of the CWT method are the indices of similarity of the chosen wavelet and the analyzed signal. It is well known that the real Morlet wavelet is similar to the damped oscillating waveform and hence matches the transient vibrations formed due to the impulsive engagement of the rolling component with point or line defects of the bearing race. The standard manner of representing the CWT is to use a two- or three-dimensional plot called a scalogram which plots the modulus of the wavelet transform as functions of location over a range of scales [49], [50]. In 2009 H. Hong and M. Liang [51] studied the severity assessment of fault for REBs by the combined application of CWT and Lempel-Ziv complexity. The authors tried to measure the severity of the bearing fault by using results obtained from the continuous wavelet transform. In the first stage, the CWT identified the best characteristic features and eradicated the presence of noise and unwanted signals as far as possible. In the second stage, the Lempel-Ziv complexity numbers were computed, and the severity of the bearing defect was measured effectively. Even though the CWT is shift-insensitive, it is computationally expensive. It should be considered when using CWT in FD of machine elements like REB.
Table 5The main differences between traditional analysis and AI-based analysis
Factors | Traditional analysis | Artificial intelligence |
Time as a factor | Prediction of a single occurrence Effective at non-time changing, steady-state occurrences In transient events, when time is a variable rather than an index, the system is unable to cope | The entire time series is treated as though it were a single event Excellent for contrasting steady-state and transient occurrences |
User expertise required | It is critical to have access to appropriate data in order to construct a model The effectiveness of the model is determined by the user's ability | Relevant data and essential features are automatically recognized The data is directly linked to the process Value can be captured right away |
Identification of diagnostic data | The fault diagnostic library must be explicitly declared For diagnosis, key features are estimated by the user and incorporated into the model | Fault diagnostic data is part of the event itself Features of the first, second, and third order are generated automatically User input is integrated into the system so that it can learn from its experience |
Model training and data pre-processing | Manually detecting and excluding poor points from a data collection is used to train a model | The model automatically detects normal behavior and standard deviations |
3.4.6.2. Discrete wavelet transform (DWT)
Wavelets offer time-scale data of the signal empowering the extraction of characteristic features that vary with time. This behavior makes the wavelets a perfect means for analyzing transient or non-stationary signals. The discrete wavelet transform is derivable from a CWT. DWT can give results with a higher resolution at different frequencies by removing redundant information [52]. S. Sharma et al. in 2015 [53] investigated the fault diagnostics of the rolling contact bearing in a variable, invariable speed, and load requirements. The characteristic extraction of vibration signal in time and frequency domains was performed by DWT, and the character reduction to remove the redundancy of the signal was carried out by Orthogonal Fuzzy Neighborhood Discriminative Analysis (OFNDA). The classification of defects and prognostication of the conditions of the elements was conducted by the Dynamic Recurrent Neural Network (DRNN). Even though the computational speed of DWT is more, it ignores the high-frequency part of the vibration signal, and it concentrates only on the low-frequency part in each decomposition level. This may adversely affect the efficiency of the FD procedure.
3.4.6.3. Wavelet packet transform (WPT)
Wavelet packet transform is an innovative time-frequency analysis procedure, which is having vast applications in the defect diagnostics of rotating machines. WPT decomposes a signal into several wavelet packets in the form of a full binary tree. It enhances the weak transients from noisy signals [54], [55]. In 2002 two researchers [56] studied the fault diagnostics of REBs by the implementation of wavelet packets. Following the paper, the WPT was employed as a symmetric means to analyze vibration signals coming out of the defective bearings. The objective of the research included the provision of a time-frequency breakdown of vibration signal and the selection of components that carries significant analytical information. This method could be conducted with minimal user intervention because of the flexibility of WPT and the efficient parameter selection eligibility. WPT resolves the limitations of DWT, it can decompose high-frequency as well as low-frequency parts of the vibration signal, but WPT is shift-sensitive. In 2005 Z. K. Peng et al. [57] published an article on the fault diagnosis of REB by comparing an upgraded HHT along with a wavelet transform. The researchers proposed an improved HHT method with the aid of WPT and intrinsic mode functions. The role of WPT in the suggested method was a preprocessor to break down the vibration signal coming from defective bearing into a series of narrowband signals. After that, IMFs were generated with the help of EMD. Finally, useful IMFs were selected by removing undesired IMFs in the selection process.
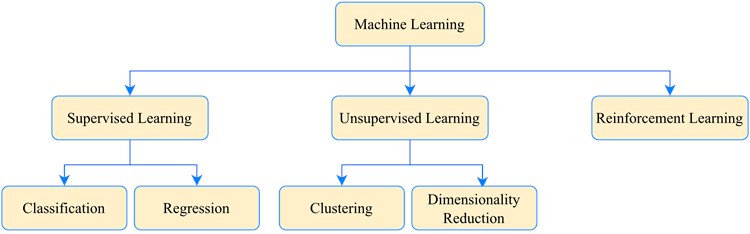
Fig. 4Different classes of Machine learning
3.4.6.4. Tunable Q-factor wavelet transform (TQWT)
TQWT is a newly designed, updated version of the wavelet transform that, depending on the Q-factor number, may break down any vibration signal into low Q-factor, high Q-factor, and residual components [58]. A. Anwarsha and T. Narendiranath Babu wrote a review article on the role of TQWT in the fault diagnosis of rolling element bearings [59]. In 2014 H. Wang et al. [60] published an article on early weak defect feature extraction of the REB employing Ensemble Empirical Mode Decomposition (EEMD) with the application of tunable Q-factor wavelet transform. By this technique, the decomposition of the collected signal is carried out by using EEMD. Then the application of TQWT to the selected intrinsic mode functions with the biggest kurtosis value. Furthermore, envelope demodulation is employed for the carefully chosen lowest Q-factor element. TQWT can overcome the limitations of the conventional WT, the quality factor of TQWT can be tuned easily, but it is computationally expensive.
4. Artificial intelligence for fault classification
The paper discussed the many types of signal processing approaches used in vibration analysis in the preceding sections. All of the approaches require the assistance of a professional. The most important aspect of current condition monitoring, however, is the capability to identify and repair faults without the assistance of a human. This is where artificial intelligence enters the picture. Artificial intelligence techniques have gained great applications in the area of defect diagnostics of rotating machines because of their reliability and adaptation capabilities. Furthermore, it does not necessitate complete previous substantial familiarity, which might be hard to acquire in actual practice. K-nearest neighbor, naive bayes classifier, support vector machine, deep learning, and artificial neural network are the important artificial intelligent techniques for fault identification [61]. A comparative study [62] was conducted on the effectiveness of ANN, SVM, and Gaussian Regression Process in estimating the bearing’s remaining useful life. The numerous artificial intelligence methods utilized in the fault diagnostics of REBs are described in this section.
Artificial intelligence is demonstrated when a machine can execute a task that was previously accomplished by a human and was assumed to require the ability to learn, reason, and solve problems. Artificial intelligence (AI) is the ability of machines to appear to think for themselves. There are two sorts of AI techniques in general utilized in REB fault diagnosis. They're called Machine Learning and Deep Learning, respectively. The following section explains these concepts.
4.1. Machine learning algorithms
Machine learning is a subset of artificial intelligence that focuses on machines' capability to receive a collection of data and learn for themselves, modifying algorithms as they get a better understanding of the data they're processing. Machine learning and artificial intelligence are frequently used interchangeably. Machine learning is divided into three categories: supervised learning, unsupervised learning, and reinforcement learning. Supervised learning is a sort of machine learning that learns from training data with learning targets that are labeled. It usually makes predictions based on a learned mapping that generates an output for each input. There are many different types of mapping, such as decision trees, logistic regression, support vector machines, etc. There are two types of supervised learning. The first is known as classification, and the second is known as regression. When the output variable is a category, such as red or blue, faulty or healthy, the problem is called a classification problem. A classification model attempts to get some decisions from the examined data. The goal of regression is to predict the value of each data point, for example, prediction of temperature, age, etc. As a result, it's a method for analyzing the correlation between a scalar dependent variable and one or more explanatory variables. Unsupervised learning entails constructing an internal representation of the input, such as finding clusters or extracting features. The program must determine the data patterns on its own because no information about the correct output labels is available. As a result, the input is unlabeled, and the algorithm must figure out what it is. Clustering or dimensionality reduction are two examples of unsupervised learning. Clustering is a crucial topic in unsupervised learning since it involves identifying a structure or pattern in a set of uncategorized data. The process of lowering the number of random variables by establishing a set of principal variables in the problem under consideration is referred to as dimensionality reduction. The information available for training in reinforcement learning is truly intermediate between supervised and unsupervised learning. As a result, instead of training samples that show the proper output for a provided input. The training data are considered to provide merely a rough indicator of whether or not a given action is correct. So, we're concerned with the problem of finding the best course of action in a given situation. The following are some of the most often utilized machine learning algorithms in REB's fault diagnosis field.
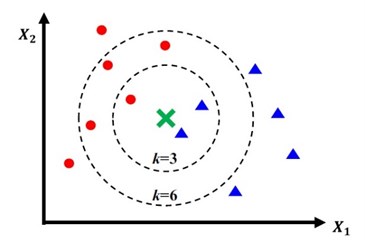
4.1.1. K-nearest neighbors (KNN)
The k-nearest neighbor technique is a simple pattern recognition methodology; it is particularly a multi-class classifier. The KNN technique is based upon the learning analogy and does not require any parameters to be chosen carefully. It is highly successful in the identification of statistical patterns, and it can accomplish better categorization accuracy for unlabeled distribution data. One of the advantages of the KNN algorithm is that it can eliminate the misclassification error to a great extent, especially when the training is carried out from a large number of data sets. Where K indicates the number of neighbors which affects the categorization accuracy of the KNN method [63]-[65]. KNN has better classification accuracy when the training dataset is larger. But then it is computationally expensive and requires more storage space.
Table 6Suitability and efficiency of various approaches for detecting early faults and low energy defects
Methods | Detection of early fault | Efficiency for low energy defects | The number of information sources |
Time domain | × | Low | 4 |
Frequency domain | √ | Low | 10 |
Cyclo-stationary | √ | Low | 3 |
Time- frequency domain | √ | Medium | 19 |
Time domain + artificial intelligence | √ | Medium | 4 |
Frequency domain + artificial intelligence | √ | Medium | 17 |
Time- frequency domain + artificial intelligence | √ | High | 23 |
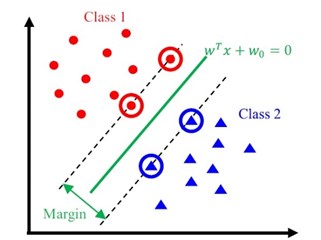
Fig. 5Example of k-nearest neighbor and Support vector machine
4.1.2. Support vector machine (SVM)
A support vector machine is an efficient tool in the area of machine defect diagnostics, which is capable of making a consistent decision for a lesser quantity of datasets and has a better generalization ability. In the condition monitoring process, SVM is used to find specific patterns in obtained signals, which are subsequently categorized based on the machine's problem incidence [66], [67]. In 2018 two researchers [68] proposed a new enhanced support vector machine categorization procedure with multi-domain characteristic features. To ameliorate the low recognition accuracy and insufficient feature extraction of current processing approaches with a single domain feature, they suggested a defect categorization algorithm through enhanced SVM with multiple domain features. In the feature extraction stage, vibration signals’ fundamental properties and condition information were extracted by applying statistical analysis, FFT, and Variation Mode Decomposition (VMD) approaches. In the feature selection stage, a meaningful sensitive feature was selected with the improved calculation efficiency by the Laplace Score Algorithm technique. In the fault identification stage, a particle swarm optimization-based SVM classification model was applied. The main limitations of SVM are, that it is a time-consuming procedure when the training dataset is too large, and it is inappropriate for multi-class classification since it is used basically for binary-class classification.
4.1.3. Naive Bayes (NB) classifier
The Naive Bayes classifier is a categorization method for defect diagnostics of the REBs, specifically based upon the Bayes rule. In other words, the NB classifier is a controlled learning-classification technique based on probability, it has achieved great popularity because of its unique classification model and outstanding classification outcome. One of the advantages of the NB classifier is that it evaluates the characteristic features of the signal from a lesser number of training data [69]-[71]. However, the NB classifier requires prior probability and strong assumptions. Furthermore, it is nearly impossible in a real-time context to assume that all predictor features are mutually independent.
Table 7Characteristics of various AI algorithms
Algorithm | Prediction speed | Training speed | Memory usage | General assessment |
Linear SVM, Logistic Regression | Fast | Fast | Small | For minor situations with linear decision boundaries, this method works well |
Decision Trees | Fast | Fast | Small | Although a good generalist, it is prone to overfitting. |
Non-linear SVM | Slow | Slow | Medium | It works well with high-dimensional data and is good for many binary problems |
Nearest Neighbour | Moderate | Minimal | Medium | Lower precision, but simpler to use and comprehend |
Naïve Bayes | Fast | Fast | Medium | For multi-class predictions, this approach is widely used |
Neural Network | Moderate | Slow | Medium to Large | Classification, compression, recognition, and forecasting are popular applications |
4.1.4. Artificial neural network (ANN)
An artificial neural network is an optimization technique inspired by the human brain. It can be used for processing information such as data classification and pattern recognition. ANN is one of the computational models in artificial intelligence techniques, particularly an interrelated assembly of uncomplicated processing components, parts, and nodes. In various ANN operations, processing of the data is being conducted through a single neuron, which results in slower computation. The advantages of ANN include better learning skills, noise reduction properties, and computation capabilities. Nevertheless, the successful execution of ANN-based diagnostics heavily is reliant on the appropriate choice of the nature of network structure and the number of training data that do not necessarily exist in actual practice [72]-[74]. Some researchers [75] published an overview of the application of ANN in defect diagnostics and fault classification of REB. Two researchers [76] made a comparison study between ANN and SVM in defect classification and FD of bearings. They found that SVM has some advantages in classification accuracy over ANN. In 2003 B. Samanta and K. R. Al-Balushi [77] published an article on fault diagnostic of the rolling-element bearing by the implementation of artificial neural networks in time-domain features. The characteristic features for ANN inputs were collected from time-domain vibration signals of regular and faulty bearings. In a study [78] the remaining useful life of slow-speed bearings was estimated by the application of multilayer ANN and linear regression classifier by analyzing AE signals. However, the limitations of ANN such as hardware dependency, unexplained functioning of the network, the complexity of showing a problem to the network, etc. to be considered when selecting ANN for fault classification of machine elements like REB.
Fig. 6Operation of artificial neural network
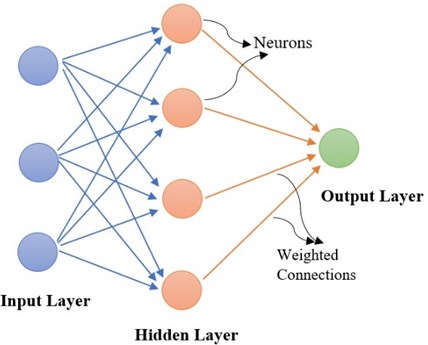
Fig. 7Structure of the fuzzy logic system
4.1.5. Fuzzy logic system
Fuzzy logic is a potential tool for decision-making to solve problems with imprecision and uncertainties. A classical set allows answering two variables either true (1) or false (0), whereas a fuzzy set allows answering the range between zero and one [79]. Fuzzy sets can be used as the fault classification tool in the area of defect diagnosis of REB. In 2019 F. Gougam et al. [80] suggested a hybrid technique for FD of bearings by the combined application of the EWT and fuzzy logic system. The proposed method helped them to detect the early-stage fault under variable operating conditions. Two researchers [81] put forward a new method for FD of REB by taking the advantage of fuzzy sets, hierarchical entropy, and support vector machines. A study [82] was conducted on rotating machinery by incorporating the applications of fuzzy logic and adaptive filter technique to detect and assess the severity of the faults. However, a major drawback of fuzzy logic is that it completely depends on human knowledge and expertise. Moreover, it is required to update the fuzzy rules regularly in the control system.
4.1.6. Particle swarm optimization (PSO)
Particle swarm optimization is an evolutionary and stochastic optimization technique inspired by nature that is used to address computationally difficult optimization issues [83]. Y. Cheng et al. [84] used the PSO algorithm in defect identification of REB to solve the inverse filter of the deconvolution problem. A study [85] was conducted on FD of REB with the combined application of PSO as a feature selection method and SVM as a classification method. In 2016 C. Yi et al. [86] conducted experiments on the fault feature extraction of REB by taking the advantage of PSO and variational mode decomposition. However, PSO has a low convergence rate in the iterative process, and it easily falls into local optima when it is dealing with high-dimensional problems. Moreover, it requires human knowledge and expertise.
4.2. Deep learning architectures
With the rise of the Internet of Things, intelligent manufacturing has shifted its attention to the collection of massive amounts of data known as big data [87]. Big data analytics is the practice of analyzing large amounts of data to find hidden patterns, unknown relationships, and other insights. Its main purpose is to assist people or machines in making intelligent decisions by evaluating big data streams from many sources [88]. Deep learning technology has been added to address the existing issues of prognostics and diagnostics caused by the vast, diverse, high-speed, and variable big data generated by industrial systems. PHM technology based on deep learning has been used to diagnose faults and assess the health of motors, gearboxes, bearings, and other mechanical components, and has outperformed previous methods [89]-[92].
Table 8Different AI-based methods with benefits and drawbacks
AI-Based Methods | Benefits | Drawbacks |
k-NN | Simple method. It's versatile, and it can be used for regression and classification. High precision | It is computationally expensive and requires more storage space |
SVM | High accuracy and compatibility with big and complicated datasets | Because it is primarily utilized for binary-class classification, it is ineffective for multi-class classification |
NB | Missing values aren't a problem, and there's no need for a lot of storage capacity | The NB classifier requires prior probability and strong assumptions |
ANN | Classification accuracy is high, and complex nonlinear functions are well approximated | Complicated design procedure, huge network processing takes a long time. There are a lot of parameters, and it's simple to overfit |
Fuzzy | Strong sturdiness, a basic style, and an easy-to-understand layout | It's difficult to get the knowledge rules, and it's even harder to figure out what the correct membership function is |
PSO | It has a simple premise, is straightforward to apply, is robust to control parameters, and is computationally efficient | PSO has a low convergence rate in the iterative process, and it easily falls into local optima when it is dealing with high dimensional problems |
Deep Learning | The feature extractor is not required for learning features and spotting flaws, and the deep architecture allows for learning more complicated structures from data | It necessitates a significant quantity of sample data, it is expensive to train for a long time due to the complex data models, etc |
The general methods of fault diagnostics of rolling element bearings were discussed in the preceding sections. But in this section, we’ll go over some of the most cutting-edge techniques in this field. For this, the most recent four years’ worth of research publications has been used. Although the benefits of AI approaches used in fault classification are discussed in the previous part, this section covers a much larger version of the most powerful deep learning techniques. Deep learning is a subset of machine learning in which a model learns to do categorization tasks using only images, numbers, text, or voice as input. Neural network architecture is generally utilized to execute deep learning. The term “deep” refers to the network’s number of layers; the more layers, the deeper the network. Deep neural networks can have more than hundreds of layers, whereas conventional neural networks have just two or three.
Deep learning is state-of-the-art because of its classification accuracy. This level of precision is made possible by three factors: One, easier access to large amounts of labeled data, two, increased computer power, and three, expert-built models. Inspired by biological nerve systems, a deep neural network integrates numerous nonlinear processing layers, using simple pieces functioning in parallel. An input layer, multiple hidden layers, and an output layer make up the structure. Each hidden layer utilizes the output of the preceding layer as its input, and the layers are linked by the nodes or neurons. The following are some of the most cutting-edge deep learning algorithms in the field of rolling element bearing’s fault classification.
4.2.1. Deep belief networks (DBN)
A DBN is a generative graphical framework made up of numerous layers of latent variables, most of which are binary, that can denote hidden characteristics in input observations. Like an RBM (Restricted Boltzmann Machine) model, the link between the leading two levels of a DBN is undirected, and so a DBN with one hidden layer is just an RBM. Except for the final, all of the remaining connections in DBM are directed graphs to the input layer. J. Tao et al. [93] wrote an article on the fault detection of rolling element bearings on the basis of deep belief networks. In 2020, S. Liu et al. [94] suggested a fault identification procedure of REB based on the enhanced convolutional DBN.
4.2.2. Autoencoders
Autoencoder is a three-layer neural network that uses its output layer to try to recreate its input. As a result, an autoencoder's output layer has an equal number of units as the input layer. There are two aspects to the autoencoder technology. Between the input and the hidden layer is the encoder, and between the hidden and the output layer is the decoder. As a result, during the encoding phase, the input trials are frequently recorded in a lower-dimensional feature space. This procedure can be done until the necessary feature dimensional space is obtained. In the decoding phase, we use reverse processing to regenerate the true features from the lower-dimensional features. In a study [95] an autoencoder-based FD of REB using a deep graph convolutional network (DGCN) was proposed. In this method, acoustic signals were collected as graphs and fed into DGCN, where the features were extracted. In 2018 A. Prosvirin et al. [96] studied autoencoder-based FD of bearings by the application of a convolution neural network with kurtogram representation. In this study, they transformed the one-dimensional AE signal into a two-dimensional kurtogram representation that allows CNN to extract high-quality features. Based on an Improved Stack Autoencoder (SAE) and SVM, M. Cui et al. [97] suggested a solution for the FD of rolling bearings. In [98], a unique SAE model for bearing problem diagnostics is created employing a dynamic learning rate, which effectively overcomes the fixed learning rate's drawbacks.
4.2.3. Convolutional neural network (CNN)
The most well-known convolutional neural networks are the next deep architecture. An input layer, many alternating convolutions and max-pooling layers, one fully connected layer, and one classification layer make up the CNN's overall design. The convolutional layers and the subsampling or pooling layers permit the network to pick up filters that are particular to certain regions of the data. The convolution layers assist the framework in preserving the spatial arrangement of pixels found in any picture. The network can summarize the pixel information thanks to the pooling layers. In 2017 L. H. Wang et al. [99] wrote an article on the application of a convolution neural network in the fault diagnostics of motors. In this paper, the advantages of CNN are that it is highly efficient in pattern recognition, it does not require the pre-treatment of input images and it is easily adaptable in the translation of input images. The original signal is used as input in [100] to create a unique network structure based on singular value decomposition (SVD) and 1DCNN, which allows for intelligent identification of bearing problems. Using a Two-Dimensional Convolutional Neural Network (2DCNN), X. Peng et al. [101] devised a method for diagnosing rolling bearing faults. For bearing fault diagnostics, A. Khorram et al. [102] presented an end-to-end CNN plus LSTM deep learning technique.
Fig. 8Convolution neural network architecture
Fig. 9Recurrent neural network architecture
4.2.4. Recurrent neural networks (RNN)
RNNs are feed-forward networks that span many time steps. A network node collects existing data inputs as well as hidden node values obtaining information from prior time steps at any given time. RNNs are special in that they may operate on a sequence of vectors across time. Sequences could be used in the input, output, or, in the most common situation, both. The three types of RNNs most typically utilized in the FD of REB are Long Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), and Bidirectional Recurrent Neural Networks (BRNN). The upgraded classic recurrent neural network (RNN), Long Short-Term Memory (LSTM), can acquire the whole historical information of input data. However, there are certain drawbacks to RNN, such as the possibility of gradient disappearance or gradient explosion during backpropagation. Input, output, and forget gates are added to the LSTM to solve these concerns. In recurrent neural networks, a gated recurrent unit (GRU) is a gating mechanism that can be employed in both their complete form and numerous reduced variations. Because they don't have an output gate, they have a smaller number of parameters than LSTM. Bi-directional RNNs forecast or label every element of a series on the basis of the element's past and future perspectives using a finite sequence. Concatenating the outputs of two RNNs, one processing the sequence from left to right and the other from right to left, accomplishes this.
For the shortcomings of existing fault detection methods, an end-to-end intelligent fault diagnosis procedure for the bearing is suggested in [103], which combines a long short-term memory network (LSTM) with a one-dimensional CNN. X. Chen et al. [104] offered a neural network with automated feature learning that accepts raw vibration signals as inputs and employs two CNNs with varying kernel sizes to collect distinct frequency signal properties. Then, based on the learned attributes, LSTM was employed to determine the defect kind. Using a recurrent neural network, Z. An et al. [105] proposed a novel bearing intelligent failure diagnostic framework for time-varying operating situations. Multi-sensor bearing defect diagnostics based on a 1D convolutional LSTM network were proposed in [106].
4.2.5. Transfer learning
Transfer learning is a concept in deep learning that involves taking the knowledge learned while addressing one problem and employing it to a similar but different problem. For instance, the skills learned while learning to distinguish cars can be applied to recognizing trucks to some extent. And this is an exciting breakthrough in the field of deep neural networks. So, there are two phases here. The first step is pre-training, which is training a network with a large quantity of data so that the model may learn the weights and biases, and then fine-tuning, which entails transferring these weights to another network for testing or training a similar new model. In addition, rather than starting from scratch, the network can use pre-trained weights. Z. Wang et al. [107] proposed a method for the fault detection of REB with the help of transfer learning techniques. Some researchers proposed a method for the fault detection of bearings based on the transfer learning approach [108].
We’re currently discussing different types of deep learning methods. Deep Forward Networks, Restricted Boltzmann Machines, Generative Adversarial Networks, Deep Reinforcement Learning, and Bayesian Deep Learning are some of the other deep learning methods accessible. But we only covered the methods for fault classification of rolling element bearings in this article. The deep learning algorithms have better performance in the modeling of high-level data processing [109]. However, there are still some drawbacks of deep learning exists such as it necessitates a significant quantity of sample data, it is expensive to train for a long time due to the complex data models, etc.
5. Summary and discussion
Rolling element bearing is an indispensable component in every machine, so its fault diagnosis is very important. Data acquisition, signal processing, and fault classification are the three main components of the fault diagnostic technique. Some of the approaches used in signal processing and fault categorization are described in this paper. Every day, new developments in this field emerge. It's nearly hard to construct a summary article that covers all of the papers in the collection. However, practically all of the most common ways are covered. The advantages and disadvantages of each approach are listed in the tables, making it very easy for readers to understand the various methods.
Until about a decade ago, any of the above-mentioned approaches were used to diagnose and classify most faults. However, the current trend is to combine multiple methods to achieve superior fault classification findings. Artificial Intelligence (AI) is also becoming more prevalent in this field. With the advancement of artificial intelligence in this field, it is now possible to detect flaws ahead of time without the involvement of humans. Table 8 summarizes the benefits and drawbacks of the most generally used artificial intelligence approaches for defect identification. Today, academics are attempting to learn more about deep learning's potential and how to apply it to improve defect diagnostics. In addition, this article included table 9 which summarized the work of numerous researchers, including the main objectives, techniques used, and their main findings.
The information for this article was gathered from research and review papers published in peer-reviewed publications. A review of over a hundred research papers reveals that there are still some gaps in this field. The majority of papers deal with a single fault, with only a few dealings with multiple faults. It's also worth noting that many articles clearly indicate the presence of a fault but do not specify the fault's exact size or width. Likewise, when we come to AI-based methods, deep learning, has numerous advantages, but its computational complexity remains a challenge. To address these issues, new ways must be introduced into the field.
Table 9Techniques used by various researchers with their objectives and main findings
References | Main objectives | Techniques used | Main findings |
[8] | Fault diagnostics of REB | Matching pursuit | Lowers the redundancy of the dictionary, easy interpretation of results |
[14] | Vibration analysis of REB defects | Time domain | Beneficial in finding tiny faults in roller bearings |
[21] | Signal processing techniques | Modified cepstrum analysis | Not very sensitive to minor Fourier components |
[29] | Analysis of REB vibration signals | Cyclo-stationary analysis | More effective, better computation capability |
[31] | REB fault diagnosis | Local characteristic-scale decomposition-teager energy operator | Better performance under fluctuating conditions |
[32] | Fault detection of ball bearing | STFT | Effective as a diagnostic tool, perfection in spike detection |
[33] | Rolling bearing FD | STFT + Deep learning | Easy to apply, robust, and better diagnostic performance |
[36] | REB diagnosing method | EMD | Better fault detection capability at the early stages |
[39] | Compound faults detection method for REB | EWT + chaotic oscillator | Potential and adequate for multi-defect diagnostics of REB |
[42] | FD of bearings | WVD + EMD | An effective method in bearing fault diagnosis |
[48] | Singularity analysis for bearing fault | CWT | Powerful in isolating the fault-related signature |
[52] | Detection of ball bearing fault | DWT | Beneficial in single and multiple fault identification |
[55] | Rolling bearing FD | DBN + Dual-Tree Complex WPT | Does not require manual feature selection, reliable fault detection |
[64] | Fault diagnosis of bearing | KNN + fuzzy C-means | More accurate recognition, improved efficiency |
[65] | Fault diagnostics of REB | AE + Hilbert Huang Transform + asymmetric proximity function-KNN | More precise classification, More reliable |
[67] | Rolling bearing FD | SVM + multiscale permutation entropy | Better recognition accuracy, efficient in detecting the different categories of faults |
[71] | Bearing defect diagnostics | NB + enhanced independence of data | Enhanced condition monitoring |
[72] | REB multi-fault diagnosis | WT + Hidden Markov model | Better output in pattern recognition |
[109] | Defect pattern recognition in REB | Hierarchical diagnosis network + DBN | More reliable in multi-stage diagnosis, efficient to eliminate overlapping problems |
[111] | Damage detection of REB | Discrete impulse frequency translation | The technique is applicable to all types of REB |
[114] | Diagnosis and monitoring of REB | Power Spectral Density analysis + ANN | Efficient fault identification |
[115] | FD of low-speed bearing | Multiclass relevance vector machine | More suitable in the real application, better computational ability |
[116] | Multi-fault diagnostics of ball bearing | FFT + wavelet energy entropy means + RMS | Good computational efficiency, better resolution |
[117] | Extracting fault characteristics | WPT + Kurtogram | Precisely match the fault characteristics for various noisy signals |
[118] | REB fault diagnosis | WPT + manifold learning | Effective and reliable for early-stage fault detection |
[119] | Bearing FD | Multi-scale morphology analysis | Can be used to determine damage modes |
[120] | Diagnostics of REB defects | Envelope detection + PSO | Capable of identifying all types of faults in incipient stages |
[121] | Rolling element bearing fault classification | EMD + Multiscale dynamic time warping | Simple and reliable, necessitate a smaller number of samples, lower the period |
[122] | Enrichment of defect signature in REB | Fast non-local means algorithm | Effective bearing diagnostics against different signal-to-noise ratio |
[123] | Fault detection of aero-engine bearing | WPT + Rough set theory | Quick detection of bearing faults |
[124] | FD of rolling bearing | Discrete Hidden Markov Model | A reliable, on-site diagnosis is possible |
[125] | Bearing fault diagnosis | Wavelet packet decomposition + SVM | High recognition accuracy, easy to apply |
[126] | Rolling element bearing fault diagnostics | Over-Complete rational dilation WT | Better performance under background noise and speed fluctuations |
[127] | Fault diagnostics of REB | Sparsogram + Lempel-Ziv | Better performance in the quantitative diagnostics |
[128] | Fault feature extraction from bearings | Improved resonance-based signal sparse decomposition | Better performance compared with conventional spectrum analysis |
[129] | REB incipient defect diagnostics | Adapted dictionary free orthogonal matching pursuit | Robust, strong adaptability, effective in analysis |
[130] | Incipient defect detection in rolling bearing | WT + Resonance-based sparse signal decomposition | Better fault feature recognition ability than regular RSSD |
[131] | Fault diagnostics of rolling bearings | Segment tensor rank decomposition | Extract the fault characteristic frequency accurately, excellent data compression capability |
[132] | Bearing fault diagnostics in variable speed conditions | Acoustic spectral imaging | Invariant to fluctuations of shaft speed |
[133] | Assessment of remaining useful life of REB | WPT + ANN | Better accuracy in the prediction of remaining useful life |
[134] | Automated bearing FD | Self-normalizing CNN | The fault detection rate is faster than traditional CNN |
[135] | Fault classification of low-speed bearings | SVM + genetic algorithm | Effective fault classification at low speed and varying load conditions |
[136] | Fault classification of ball bearing | Vibro-acoustic sensor data fusion + KNN | Increased reliability, accuracy, and robustness |
[137] | Early fault detection of REB | Optimized Kurtogram method | Effective extraction of early weak features, better performance |
[138] | Low speed bearing FD | Adaptive resilient stacked sparse autoencoder | Easy to implement, require a smaller number of data samples |
[139] | Bearing fault diagnosis | Fuzzy logic + multiscale permutation entropy | Better performance, Better accuracy |
[35], [110] | Fault diagnosis of bearings | EMD + Hilbert Transform | Better output in analyzing various frequency ranges |
[112], [113] | Early detection of defects and diagnostic monitoring in REB | High-frequency resonance technique | Suitable to detect both inner race and outer race faults at incipient stages |
6. Conclusions
An attempt has been made to summarize the various vibration analysis methodologies for fault diagnosis of rolling element bearings in this work. Every day, a slew of new techniques emerges in this discipline. As a result, writing a review paper that covers all of the methods is nearly impossible. This article summarized over a hundred peer-reviewed research publications that explained how to detect faults in rolling element bearings using time-domain, frequency-domain, time-frequency domain, cyclo-stationary analysis, and artificial intelligence-based methodologies. RMS in the time domain, FFT in the frequency domain, and WT in the time-frequency domain are the most often utilized techniques in REB fault diagnostics, according to the published articles. Similarly, in AI-based approaches, SVM is the most often used methodology. However, more studies on deep learning have recently been published. In this article, the aforementioned method’s advantages and disadvantages are clearly outlined in distinct tables. Therefore, this paper is valuable for research students and people who want to learn more about vibration analysis methodologies for rolling element bearing failure diagnosis.
References
-
M. Hamadache, J. H. Jung, J. Park, and B. D. Youn, “A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: shallow and deep learning,” JMST Advances, Vol. 1, No. 1-2, pp. 125–151, Jun. 2019, https://doi.org/10.1007/s42791-019-0016-y
-
F. Yang, W. Zhang, L. Tao, and J. Ma, “Transfer learning strategies for deep learning-based PHM algorithms,” Applied Sciences, Vol. 10, No. 7, p. 2361, Mar. 2020, https://doi.org/10.3390/app10072361
-
B. J. Hamrock and W. J. Anderson, “Rolling-Element Bearings,” NASA Reference Publication, 1983.
-
N. Tandon and A. Choudhury, “A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings,” Tribology International, Vol. 32, No. 8, pp. 469–480, Aug. 1999, https://doi.org/10.1016/s0301-679x(99)00077-8
-
Y. H. Ali, R. Abd Rahman, and R. I. Raja Hamzah, “Acoustic emission signal analysis and artificial intelligence techniques in machine condition monitoring and fault diagnosis: A review,” Journal Technology, Vol. 69, No. 2, pp. 121–126, Jun. 2014, https://doi.org/10.11113/jt.v69.3121
-
A. Rai and S. H. Upadhyay, “A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings,” Tribology International, Vol. 96, pp. 289–306, Apr. 2016, https://doi.org/10.1016/j.triboint.2015.12.037
-
A. Kumar and R. Kumar, “Role of signal processing, modeling and decision making in the diagnosis of rolling element bearing defect: a review,” Journal of Nondestructive Evaluation, Vol. 38, No. 1, pp. 1–29, Mar. 2019, https://doi.org/10.1007/s10921-018-0543-8
-
L. Cui, J. Wang, and S. Lee, “Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis,” Journal of Sound and Vibration, Vol. 333, No. 10, pp. 2840–2862, May 2014, https://doi.org/10.1016/j.jsv.2013.12.029
-
A. R. Mohanty, Machinery Condition Monitoring: Principles and Practices. CRC Press, 2014, https://doi.org/10.1201/9781351228626
-
F. Elasha, M. Greaves, D. Mba, and A. Addali, “Application of acoustic emission in diagnostic of bearing faults within a helicopter gearbox,” in Procedia CIRP, Vol. 38, pp. 30–36, 2015, https://doi.org/10.1016/j.procir.2015.08.042
-
Z. Liu and L. Zhang, “A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings,” Measurement, Vol. 149, p. 107002, Jan. 2020, https://doi.org/10.1016/j.measurement.2019.107002
-
Z. Mo, J. Wang, H. Zhang, X. Zeng, H. Liu, and Q. Miao, “Vibration and acoustics emission based methods in low-speed bearing condition monitoring,” in 2018 Prognostics and System Health Management Conference (PHM-Chongqing), pp. 871–875, Oct. 2018, https://doi.org/10.1109/phm-chongqing.2018.00156
-
I. El-Thalji and E. Jantunen, “A summary of fault modelling and predictive health monitoring of rolling element bearings,” Mechanical Systems and Signal Processing, Vol. 60-61, pp. 252–272, Aug. 2015, https://doi.org/10.1016/j.ymssp.2015.02.008
-
Tahsin Doğuer and J. Strackeljan, “Vibration analysis using time domain methods for the detection of small roller bearing defects,” in 8th International Conference on Vibrations in Rotating Machines, 2009.
-
Shyam Patidar and Pradeep Kumar Soni, “An overview on vibration analysis techniques for the diagnosis of rolling element bearing faults,” International Journal of Engineering Trends and Technology, Vol. 4, No. 5, pp. 1804–1809, May 2013.
-
B. Sreejith, A. K. Verma, and A. Srividya, “Fault diagnosis of rolling element bearing using time-domain features and neural networks,” in 2008 IEEE Region 10 and the Third international Conference on Industrial and Information Systems (ICIIS), No. 1, pp. 1–6, Dec. 2008, https://doi.org/10.1109/iciinfs.2008.4798444
-
A. Srividya, A. K. Verma, and B. Sreejith, “Automated diagnosis of rolling element bearing defects using time-domain features and neural networks,” International Journal of Mining, Reclamation and Environment, Vol. 23, No. 3, pp. 206–215, Sep. 2009, https://doi.org/10.1080/17480930902916437
-
I. Adam, “Complex wavelet transform application to denoising,” Politehnica University of Timisoara Université De Rennes, 2010.
-
V. K. Rai and A. R. Mohanty, “Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform,” Mechanical Systems and Signal Processing, Vol. 21, No. 6, pp. 2607–2615, Aug. 2007, https://doi.org/10.1016/j.ymssp.2006.12.004
-
R. B. Randall, “A history of cepstrum analysis and its application to mechanical problems,” Mechanical Systems and Signal Processing, Vol. 97, pp. 3–19, Dec. 2017, https://doi.org/10.1016/j.ymssp.2016.12.026
-
S. A. Mcinerny and Y. Dai, “Basic vibration signal processing for bearing fault detection,” IEEE Transactions on Education, Vol. 46, No. 1, pp. 149–156, Feb. 2003, https://doi.org/10.1109/te.2002.808234
-
C. Mishra, A. K. Samantaray, and G. Chakraborty, “Rolling element bearing fault diagnosis under slow speed operation using wavelet de-noising,” Measurement, Vol. 103, pp. 77–86, Jun. 2017, https://doi.org/10.1016/j.measurement.2017.02.033
-
M. Seera, M. L. D. Wong, and A. K. Nandi, “Classification of ball bearing faults using a hybrid intelligent model,” Applied Soft Computing, Vol. 57, pp. 427–435, Aug. 2017, https://doi.org/10.1016/j.asoc.2017.04.034
-
N. T. van der Merwe and A. J. Hoffman, “A modified cepstrum analysis applied to vibrational signals,” in International Conference on Digital Signal Processing, 2002, https://doi.org/10.1109/icdsp.2002.1028229
-
K. F. Al-Raheem, A. Roy, K. P. Ramachandran, D. K. Harrison, and S. Grainger, “Rolling element bearing fault diagnosis using laplace-wavelet envelope power spectrum,” EURASIP Journal on Advances in Signal Processing, Vol. 2007, No. 1, pp. 1–14, Dec. 2007, https://doi.org/10.1155/2007/73629
-
C.-S. Park, Y.-C. Choi, and Y.-H. Kim, “Early fault detection in automotive ball bearings using the minimum variance cepstrum,” Mechanical Systems and Signal Processing, Vol. 38, No. 2, pp. 534–548, Jul. 2013, https://doi.org/10.1016/j.ymssp.2013.02.017
-
D. Ibarra-Zarate, O. Tamayo-Pazos, and A. Vallejo-Guevara, “Bearing fault diagnosis in rotating machinery based on cepstrum pre-whitening of vibration and acoustic emission,” The International Journal of Advanced Manufacturing Technology, Vol. 104, No. 9-12, pp. 4155–4168, Oct. 2019, https://doi.org/10.1007/s00170-019-04171-6
-
A. Amini, M. Entezami, and M. Papaelias, “Onboard detection of railway axle bearing defects using envelope analysis of high frequency acoustic emission signals,” Case Studies in Nondestructive Testing and Evaluation, Vol. 6, pp. 8–16, Nov. 2016, https://doi.org/10.1016/j.csndt.2016.06.002
-
I. Antoniadis and G. Glossiotis, “Cyclostationary analysis of rolling-element bearing vibration signals,” Journal of Sound and Vibration, Vol. 248, No. 5, pp. 829–845, Dec. 2001, https://doi.org/10.1006/jsvi.2001.3815
-
P. K. Kankar, S. C. Sharma, and S. P. Harsha, “Fault diagnosis of rolling element bearing using cyclic autocorrelation and wavelet transform,” Neurocomputing, Vol. 110, pp. 9–17, Jun. 2013, https://doi.org/10.1016/j.neucom.2012.11.012
-
H. Liu, X. Wang, and C. Lu, “Rolling bearing fault diagnosis based on LCD-TEO and multifractal detrended fluctuation analysis,” Mechanical Systems and Signal Processing, Vol. 60-61, pp. 273–288, Aug. 2015, https://doi.org/10.1016/j.ymssp.2015.02.002
-
M. Cocconcelli, R. Zimroz, R. Rubini, and W. Bartelmus, “STFT based approach for ball bearing fault detection in a varying speed motor,” in Condition Monitoring of Machinery in Non-Stationary Operations, Berlin, Heidelberg: Springer Berlin Heidelberg, 2012, pp. 41–50, https://doi.org/10.1007/978-3-642-28768-8_5
-
H. Liu, L. Li, and J. Ma, “Rolling bearing fault diagnosis based on STFT-deep learning and sound signals,” Shock and Vibration, Vol. 2016, pp. 1–12, 2016, https://doi.org/10.1155/2016/6127479
-
H. Gao, L. Liang, X. Chen, and G. Xu, “Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization,” Chinese Journal of Mechanical Engineering, Vol. 28, No. 1, pp. 96–105, Jan. 2015, https://doi.org/10.3901/cjme.2014.1103.166
-
T. N. Babu, S. Devendiran, A. Aravind, A. Rakesh, and M. Jahzan, “Fault diagnosis on journal bearing using empirical mode decomposition,” Materials Today: Proceedings, Vol. 5, No. 5, pp. 12993–13002, 2018, https://doi.org/10.1016/j.matpr.2018.02.284
-
J. Dybała and R. Zimroz, “Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal,” Applied Acoustics, Vol. 77, No. 77, pp. 195–203, Mar. 2014, https://doi.org/10.1016/j.apacoust.2013.09.001
-
Y. Lei, J. Lin, Z. He, and M. J. Zuo, “A review on empirical mode decomposition in fault diagnosis of rotating machinery,” Mechanical Systems and Signal Processing, Vol. 35, No. 1-2, pp. 108–126, Feb. 2013, https://doi.org/10.1016/j.ymssp.2012.09.015
-
J. Ben Ali, N. Fnaiech, L. Saidi, B. Chebel-Morello, and F. Fnaiech, “Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals,” Applied Acoustics, Vol. 89, pp. 16–27, Mar. 2015, https://doi.org/10.1016/j.apacoust.2014.08.016
-
Y. Jiang, H. Zhu, and Z. Li, “A new compound faults detection method for rolling bearings based on empirical wavelet transform and chaotic oscillator,” Chaos, Solitons and Fractals, Vol. 89, pp. 8–19, Aug. 2016, https://doi.org/10.1016/j.chaos.2015.09.007
-
S. N. Chegini, A. Bagheri, and F. Najafi, “Application of a new EWT-based denoising technique in bearing fault diagnosis,” Measurement, Vol. 144, pp. 275–297, Oct. 2019, https://doi.org/10.1016/j.measurement.2019.05.049
-
S. G. Mallat and Zhifeng Zhang, “Matching pursuits with time-frequency dictionaries,” IEEE Transactions on Signal Processing, Vol. 41, No. 12, pp. 3397–3415, 1993, https://doi.org/10.1109/78.258082
-
H. Yang, J. Mathew, and L. Ma, “Fault diagnosis of rolling element bearings using basis pursuit,” Mechanical Systems and Signal Processing, Vol. 19, No. 2, pp. 341–356, Mar. 2005, https://doi.org/10.1016/j.ymssp.2004.03.008
-
H. Li, H. Zheng, and L. Tang, “Wigner-Ville distribution based on EMD for faults diagnosis of bearing,” in Fuzzy Systems and Knowledge Discovery, pp. 803–812, 2006, https://doi.org/10.1007/11881599_99
-
S. S. Refaat, H. Abu-Rub, M. S. Saad, E. M. Aboul-Zahab, and A. Iqbal, “ANN-based for detection, diagnosis the bearing fault for three phase induction motors using current signal,” in 2013 IEEE International Conference on Industrial Technology (ICIT 2013), pp. 253–258, Feb. 2013, https://doi.org/10.1109/icit.2013.6505681
-
Y. Zhou, J. Chen, G. M. Dong, W. B. Xiao, and Z. Y. Wang, “Wigner-Ville distribution based on cyclic spectral density and the application in rolling element bearings diagnosis,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 225, No. 12, pp. 2831–2847, Dec. 2011, https://doi.org/10.1177/0954406211413215
-
A. Bouzida, O. Touhami, R. Ibtiouen, A. Belouchrani, M. Fadel, and A. Rezzoug, “Fault diagnosis in industrial induction machines through discrete wavelet transform,” IEEE Transactions on Industrial Electronics, Vol. 58, No. 9, pp. 4385–4395, Sep. 2011, https://doi.org/10.1109/tie.2010.2095391
-
D. Paliwal, A. Choudhur, and T. Govandhan, “Identification of faults through wavelet transform vis-à-vis fast Fourier transform of noisy vibration signals emanated from defective rolling element bearings,” Frontiers of Mechanical Engineering, Vol. 9, No. 2, pp. 130–141, Jun. 2014, https://doi.org/10.1007/s11465-014-0298-6
-
R. Yan, R. X. Gao, and X. Chen, “Wavelets for fault diagnosis of rotary machines: A review with applications,” Signal Processing, Vol. 96, pp. 1–15, Mar. 2014, https://doi.org/10.1016/j.sigpro.2013.04.015
-
Q. Sun and Y. Tang, “Singularity analysis using continuous wavelet transform for bearing fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 16, No. 6, pp. 1025–1041, Nov. 2002, https://doi.org/10.1006/mssp.2002.1474
-
P. Shakya, A. K. Darpe, and M. S. Kulkarni, “Vibration-based fault diagnosis in rolling element bearings: ranking of various time, frequency and time-frequency domain data-based damage identication parameters,” International Journal of Condition Monitoring, Vol. 3, No. 2, pp. 53–62, Oct. 2013, https://doi.org/10.1784/204764213808146626
-
H. Hong and M. Liang, “Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform,” Journal of Sound and Vibration, Vol. 320, No. 1-2, pp. 452–468, Feb. 2009, https://doi.org/10.1016/j.jsv.2008.07.011
-
S. Prabhakar, A. R. Mohanty, and A. S. Sekhar, “Application of discrete wavelet transform for detection of ball bearing race faults,” Tribology International, Vol. 35, No. 12, pp. 793–800, Dec. 2002, https://doi.org/10.1016/s0301-679x(02)00063-4
-
S. Sharma, W. Abed, R. Sutton, and B. Subudhi, “Corrosion fault diagnosis of rolling element bearing under constant and variable load and speed conditions,” IFAC-PapersOnLine, Vol. 48, No. 30, pp. 49–54, 2015, https://doi.org/10.1016/j.ifacol.2015.12.352
-
J. L. Ferrando Chacon, V. Kappatos, W. Balachandran, and T.-H. Gan, “A novel approach for incipient defect detection in rolling bearings using acoustic emission technique,” Applied Acoustics, Vol. 89, pp. 88–100, Mar. 2015, https://doi.org/10.1016/j.apacoust.2014.09.002
-
H. Shao, H. Jiang, F. Wang, and Y. Wang, “Rolling bearing fault diagnosis using adaptive deep belief network with dual-tree complex wavelet packet,” ISA Transactions, Vol. 69, pp. 187–201, Jul. 2017, https://doi.org/10.1016/j.isatra.2017.03.017
-
N. G. Nikolaou and I. A. Antoniadis, “Rolling element bearing fault diagnosis using wavelet packets,” NDT and E International, Vol. 35, No. 3, pp. 197–205, Apr. 2002, https://doi.org/10.1016/s0963-8695(01)00044-5
-
Z. K. Peng, P. W. Tse, and F. L. Chu, “A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing,” Mechanical Systems and Signal Processing, Vol. 19, No. 5, pp. 974–988, Sep. 2005, https://doi.org/10.1016/j.ymssp.2004.01.006
-
I. W. Selesnick, “Wavelet transform with tunable Q-factor,” IEEE Transactions on Signal Processing, Vol. 59, No. 8, pp. 3560–3575, Aug. 2011, https://doi.org/10.1109/tsp.2011.2143711
-
A. Anwarsha and T. Narendiranath Babu, “A review on the role of tunable Q-Factor wavelet transform in fault diagnosis of rolling element bearings,” Journal of Vibration Engineering and Technologies, pp. 1–16, Apr. 2022, https://doi.org/10.1007/s42417-022-00484-1
-
H. Wang, J. Chen, and G. Dong, “Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform,” Mechanical Systems and Signal Processing, Vol. 48, No. 1-2, pp. 103–119, Oct. 2014, https://doi.org/10.1016/j.ymssp.2014.04.006
-
R. Liu, B. Yang, E. Zio, and X. Chen, “Artificial intelligence for fault diagnosis of rotating machinery: A review,” Mechanical Systems and Signal Processing, Vol. 108, pp. 33–47, Aug. 2018, https://doi.org/10.1016/j.ymssp.2018.02.016
-
M. Elforjani and S. Shanbr, “Prognosis of bearing acoustic emission signals using supervised machine learning,” IEEE Transactions on Industrial Electronics, Vol. 65, No. 7, pp. 5864–5871, Jul. 2018, https://doi.org/10.1109/tie.2017.2767551
-
L. Zhang, L. B. Jack, and A. K. Nandi, “Extending genetic programming for multi-class classification by combining K-nearest neighbor,” in IEEE International Conference on Acoustics, Speech and Signal Processing – Proceedings, 2005, https://doi.org/10.1109/icassp.2005.1416312
-
S. Dong, X. Xu, and R. Chen, “Application of fuzzy C-means method and classification model of optimized K-nearest neighbor for fault diagnosis of bearing,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 38, No. 8, pp. 2255–2263, Dec. 2016, https://doi.org/10.1007/s40430-015-0455-9
-
D. H. Pandya, S. H. Upadhyay, and S. P. Harsha, “Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN,” Expert Systems with Applications, Vol. 40, No. 10, pp. 4137–4145, Aug. 2013, https://doi.org/10.1016/j.eswa.2013.01.033
-
A. Widodo and B.-S. Yang, “Support vector machine in machine condition monitoring and fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 21, No. 6, pp. 2560–2574, Aug. 2007, https://doi.org/10.1016/j.ymssp.2006.12.007
-
Y. Li, M. Xu, Y. Wei, and W. Huang, “A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree,” Measurement, Vol. 77, pp. 80–94, Jan. 2016, https://doi.org/10.1016/j.measurement.2015.08.034
-
X. Yan and M. Jia, “A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing,” Neurocomputing, Vol. 313, pp. 47–64, Nov. 2018, https://doi.org/10.1016/j.neucom.2018.05.002
-
R. K. Sharma, V. Sugumaran, H. Kumar, and M. Amarnath, “A comparative study of naïve Bayes classifier and Bayes net classifier for fault diagnosis of roller bearing using sound signal,” International Journal of Decision Support Systems, Vol. 1, No. 1, p. 115, 2015, https://doi.org/10.1504/ijdss.2015.067279
-
V. Muralidharan and V. Sugumaran, “A comparative study of Naïve Bayes classifier and Bayes net classifier for fault diagnosis of monoblock centrifugal pump using wavelet analysis,” Applied Soft Computing, Vol. 12, No. 8, pp. 2023–2029, Aug. 2012, https://doi.org/10.1016/j.asoc.2012.03.021
-
N. Zhang, L. Wu, J. Yang, and Y. Guan, “Naive bayes bearing fault diagnosis based on enhanced independence of data,” Sensors, Vol. 18, No. 2, p. 463, Feb. 2018, https://doi.org/10.3390/s18020463
-
V. Purushotham, S. Narayanan, and S. A. N. Prasad, “Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition,” NDT and E International, Vol. 38, No. 8, pp. 654–664, Dec. 2005, https://doi.org/10.1016/j.ndteint.2005.04.003
-
N. Saravanan and K. I. Ramachandran, “Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN),” Expert Systems with Applications, Vol. 37, No. 6, pp. 4168–4181, Jun. 2010, https://doi.org/10.1016/j.eswa.2009.11.006
-
R. S. Gunerkar, A. K. Jalan, and S. U. Belgamwar, “Fault diagnosis of rolling element bearing based on artificial neural network,” Journal of Mechanical Science and Technology, Vol. 33, No. 2, pp. 505–511, Feb. 2019, https://doi.org/10.1007/s12206-019-0103-x
-
B. K. N. Rao, P. S. Pai, and T. N. Nagabhushana, “Failure diagnosis and prognosis of rolling – Element bearings using artificial neural networks: A critical overview,” in Journal of Physics: Conference Series, Vol. 364, No. 1, p. 012023, May 2012, https://doi.org/10.1088/1742-6596/364/1/012023
-
P. Agrawal and P. Jayaswal, “Diagnosis and classifications of bearing faults using artificial neural network and support vector machine,” Journal of The Institution of Engineers (India): Series C, Vol. 101, No. 1, pp. 61–72, Feb. 2020, https://doi.org/10.1007/s40032-019-00519-9
-
B. Samanta and K. R. Al-Balushi, “Artificial neural network based fault diagnostics of rolling element bearings using time-domain features,” Mechanical Systems and Signal Processing, Vol. 17, No. 2, pp. 317–328, Mar. 2003, https://doi.org/10.1006/mssp.2001.1462
-
M. Elforjani, “Estimation of Remaining Useful Life of Slow Speed Bearings Using Acoustic Emission Signals,” Journal of Nondestructive Evaluation, Vol. 35, No. 4, pp. 1–16, Dec. 2016, https://doi.org/10.1007/s10921-016-0378-0
-
K. Gowthami and L. Kalaivani, “Fault classification of induction motor bearing using adaptive neuro fuzzy inference system,” in 2019 Fifth International Conference on Electrical Energy Systems (ICEES), pp. 1–6, Feb. 2019, https://doi.org/10.1109/icees.2019.8719244
-
F. Gougam, C. Rahmoune, D. Benazzouz, and B. Merainani, “Bearing fault diagnosis based on feature extraction of empirical wavelet transform (EWT) and fuzzy logic system (FLS) under variable operating conditions,” Journal of Vibroengineering, Vol. 21, No. 6, pp. 1636–1650, Sep. 2019, https://doi.org/10.21595/jve.2019.20092
-
K. Zhu and H. Li, “A rolling element bearing fault diagnosis approach based on hierarchical fuzzy entropy and support vector machine,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 230, No. 13, pp. 2314–2322, Aug. 2016, https://doi.org/10.1177/0954406215593568
-
M. S. Islam and U. Chong, “Fault detection and severity classification based on adaptive filter and fuzzy logic,” SN Applied Sciences, Vol. 1, No. 12, pp. 1–9, Dec. 2019, https://doi.org/10.1007/s42452-019-1680-0
-
J. Kennedy and R. Eberhart, “Particle swarm optimization,” in International Conference on Neural Networks, 1995, https://doi.org/10.1109/icnn.1995.488968
-
Y. Cheng, Z. Wang, W. Zhang, and G. Huang, “Particle swarm optimization algorithm to solve the deconvolution problem for rolling element bearing fault diagnosis,” ISA Transactions, Vol. 90, pp. 244–267, Jul. 2019, https://doi.org/10.1016/j.isatra.2019.01.012
-
R. Ziani, A. Felkaoui, and R. Zegadi, “Bearing fault diagnosis using multiclass support vector machines with binary particle swarm optimization and regularized Fisher’s criterion,” Journal of Intelligent Manufacturing, Vol. 28, No. 2, pp. 405–417, Feb. 2017, https://doi.org/10.1007/s10845-014-0987-3
-
C. Yi, Y. Lv, and Z. Dang, “A fault diagnosis scheme for rolling bearing based on particle swarm optimization in variational mode decomposition,” Shock and Vibration, Vol. 2016, pp. 1–10, 2016, https://doi.org/10.1155/2016/9372691
-
J. Wang, C. Xu, J. Zhang, and R. Zhong, “Big data analytics for intelligent manufacturing systems: A review,” Journal of Manufacturing Systems, Vol. 62, pp. 738–752, Jan. 2022, https://doi.org/10.1016/j.jmsy.2021.03.005
-
K. L. Tsui, Y. Zhao, and D. Wang, “Big data opportunities: System health monitoring and management,” IEEE Access, Vol. 7, pp. 68853–68867, 2019, https://doi.org/10.1109/access.2019.2917891
-
G. Xu, D. Hou, H. Qi, and L. Bo, “High-speed train wheel set bearing fault diagnosis and prognostics: A new prognostic model based on extendable useful life,” Mechanical Systems and Signal Processing, Vol. 146, p. 107050, Jan. 2021, https://doi.org/10.1016/j.ymssp.2020.107050
-
A. P. Daga, A. Fasana, L. Garibaldi, and S. Marchesiello, “Big data management: a vibration monitoring point of view,” in 2020 IEEE International Workshop on Metrology for Industry 4.0 and IoT (MetroInd4.0&IoT), pp. 548–553, Jun. 2020, https://doi.org/10.1109/metroind4.0iot48571.2020.9138196
-
G.-Y. Lee et al., “Machine health management in smart factory: A review,” Journal of Mechanical Science and Technology, Vol. 32, No. 3, pp. 987–1009, Mar. 2018, https://doi.org/10.1007/s12206-018-0201-1
-
J. Duan, T. Shi, H. Zhou, J. Duan, J. Xuan, and J. Zhang, “A novel bearing health prognostic method based on time-frequency analysis and LSTM,” in 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Oct. 2019, https://doi.org/10.1109/phm-qingdao46334.2019.8942821
-
J. Tao, Y. Liu, and D. Yang, “Bearing fault diagnosis based on deep belief network and multisensor information fusion,” Shock and Vibration, Vol. 2016, pp. 1–9, 2016, https://doi.org/10.1155/2016/9306205
-
S. Liu, J. Xie, C. Shen, X. Shang, D. Wang, and Z. Zhu, “Bearing fault diagnosis based on improved convolutional deep belief network,” Applied Sciences, Vol. 10, No. 18, p. 6359, Sep. 2020, https://doi.org/10.3390/app10186359
-
D. Zhang, E. Stewart, M. Entezami, C. Roberts, and D. Yu, “Intelligent acoustic-based fault diagnosis of roller bearings using a deep graph convolutional network,” Measurement, Vol. 156, p. 107585, May 2020, https://doi.org/10.1016/j.measurement.2020.107585
-
A. Prosvirin, J. Kim, and J.-M. Kim, “Bearing fault diagnosis based on convolutional neural networks with kurtogram representation of acoustic emission signals,” in Advances in Computer Science and Ubiquitous Computing, Vol. 474, pp. 21–26, 2018, https://doi.org/10.1007/978-981-10-7605-3_4
-
M. Cui, Y. Wang, X. Lin, and M. Zhong, “Fault diagnosis of rolling bearings based on an improved stack autoencoder and support vector machine,” IEEE Sensors Journal, Vol. 21, No. 4, pp. 4927–4937, Feb. 2021, https://doi.org/10.1109/jsen.2020.3030910
-
H. Pan, W. Tang, J.-J. Xu, and M. Binama, “Rolling bearing fault diagnosis based on stacked autoencoder network with dynamic learning rate,” Advances in Materials Science and Engineering, Vol. 2020, pp. 1–12, Dec. 2020, https://doi.org/10.1155/2020/6625273
-
L.-H. Wang, X.-P. Zhao, J.-X. Wu, Y.-Y. Xie, and Y.-H. Zhang, “Motor fault diagnosis based on short-time fourier transform and convolutional neural network,” Chinese Journal of Mechanical Engineering, Vol. 30, No. 6, pp. 1357–1368, Nov. 2017, https://doi.org/10.1007/s10033-017-0190-5
-
Y. Wang, S. Huang, J. Dai, and J. Tang, “A novel bearing fault diagnosis methodology based on SVD and one-dimensional convolutional neural network,” Shock and Vibration, Vol. 2020, pp. 1–17, Jan. 2020, https://doi.org/10.1155/2020/1850286
-
H. Zheng, Z. Wu, S. Duan, and Y. Chen, “Research on fault diagnosis method of rolling bearing based on TCN,” in 2021 12th International Conference on Mechanical and Aerospace Engineering (ICMAE), pp. 489–493, Jul. 2021, https://doi.org/10.1109/icmae52228.2021.9522447
-
A. Khorram, M. Khalooei, and M. Rezghi, “End-to-end CNN + LSTM deep learning approach for bearing fault diagnosis,” Applied Intelligence, Vol. 51, No. 2, pp. 736–751, Feb. 2021, https://doi.org/10.1007/s10489-020-01859-1
-
H. Sun and S. Zhao, “Fault diagnosis for bearing based on 1DCNN and LSTM,” Shock and Vibration, Vol. 2021, pp. 1–17, Oct. 2021, https://doi.org/10.1155/2021/1221462
-
X. Chen, B. Zhang, and D. Gao, “Bearing fault diagnosis base on multi-scale CNN and LSTM model,” Journal of Intelligent Manufacturing, Vol. 32, No. 4, pp. 971–987, Apr. 2021, https://doi.org/10.1007/s10845-020-01600-2
-
Z. An, S. Li, J. Wang, and X. Jiang, “A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network,” ISA Transactions, Vol. 100, pp. 155–170, May 2020, https://doi.org/10.1016/j.isatra.2019.11.010
-
S. Hao, F.-X. Ge, Y. Li, and J. Jiang, “Multisensor bearing fault diagnosis based on one-dimensional convolutional long short-term memory networks,” Measurement, Vol. 159, p. 107802, Jul. 2020, https://doi.org/10.1016/j.measurement.2020.107802
-
Z. Wang, X. He, B. Yang, and N. Li, “Subdomain Adaptation transfer learning network for fault diagnosis of roller bearings,” IEEE Transactions on Industrial Electronics, Vol. 69, No. 8, pp. 8430–8439, Aug. 2022, https://doi.org/10.1109/tie.2021.3108726
-
J. Shao, Z. Huang, and J. Zhu, “Transfer learning method based on adversarial domain adaption for bearing fault diagnosis,” IEEE Access, Vol. 8, pp. 119421–119430, 2020, https://doi.org/10.1109/access.2020.3005243
-
M. Gan, C. Wang, and C.A. Zhu, “Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings,” Mechanical Systems and Signal Processing, Vol. 72-73, pp. 92–104, May 2016, https://doi.org/10.1016/j.ymssp.2015.11.014
-
D. Yu, J. Cheng, and Y. Yang, “Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings,” Mechanical Systems and Signal Processing, Vol. 19, No. 2, pp. 259–270, Mar. 2005, https://doi.org/10.1016/s0888-3270(03)00099-2
-
D. Dyer and R. M. Stewart, “Detection of rolling element bearing damage by statistical vibration analysis,” Journal of Mechanical Design, Vol. 100, No. 2, pp. 229–235, Apr. 1978, https://doi.org/10.1115/1.3453905
-
M. S. Darlow and R. H. Badgley, “Early detection of defects in rolling-element bearings,” in 1975 Automotive Engineering Congress and Exposition, Feb. 1975, https://doi.org/10.4271/750209
-
H. Prashad, M. Ghosh, and S. Biswas, “Diagnostic monitoring of rolling-element bearings by high-frequency resonance technique,” ASLE Transactions, Vol. 28, No. 4, pp. 439–448, Jan. 1985, https://doi.org/10.1080/05698198508981641
-
I. E. Alguindigue, A. Loskiewicz-Buczak, and R. E. Uhrig, “Monitoring and diagnosis of rolling element bearings using artificial neural networks,” IEEE Transactions on Industrial Electronics, Vol. 40, No. 2, pp. 209–217, Apr. 1993, https://doi.org/10.1109/41.222642
-
A. Widodo, B.-S. Yang, E. Y. Kim, A. C. C. Tan, and J. Mathew, “Fault diagnosis of low speed bearing based on acoustic emission signal and multi-class relevance vector machine,” Nondestructive Testing and Evaluation, Vol. 24, No. 4, pp. 313–328, Dec. 2009, https://doi.org/10.1080/10589750802378974
-
O. R. Seryasat, M. Aliyari Shoorehdeli, F. Honarvar, and A. Rahmani, “Multi-fault diagnosis of ball bearing using FFT, wavelet energy entropy mean and root mean square (RMS),” in 2010 IEEE International Conference on Systems, Man and Cybernetics – SMC, pp. 4295–4299, Oct. 2010, https://doi.org/10.1109/icsmc.2010.5642389
-
Y. Lei, J. Lin, Z. He, and Y. Zi, “Application of an improved kurtogram method for fault diagnosis of rolling element bearings,” Mechanical Systems and Signal Processing, Vol. 25, No. 5, pp. 1738–1749, Jul. 2011, https://doi.org/10.1016/j.ymssp.2010.12.011
-
Y. Wang, G. Xu, L. Liang, and K. Jiang, “Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 54-55, pp. 259–276, Mar. 2015, https://doi.org/10.1016/j.ymssp.2014.09.002
-
W.-J. Wang, L.-L. Cui, and D.-Y. Chen, “Multi-scale morphology analysis of acoustic emission signal and quantitative diagnosis for bearing fault,” Acta Mechanica Sinica, Vol. 32, No. 2, pp. 265–272, Apr. 2016, https://doi.org/10.1007/s10409-015-0529-z
-
S. Tyagi and S. K. Panigrahi, “An improved envelope detection method using particle swarm optimisation for rolling element bearing fault diagnosis,” Journal of Computational Design and Engineering, Vol. 4, No. 4, pp. 305–317, Oct. 2017, https://doi.org/10.1016/j.jcde.2017.05.002
-
T. Han, X. Liu, and A. C. C. Tan, “Fault diagnosis of rolling element bearings based on multiscale dynamic time warping,” Measurement, Vol. 95, pp. 355–366, Jan. 2017, https://doi.org/10.1016/j.measurement.2016.10.038
-
S. K. Laha, “Enhancement of fault diagnosis of rolling element bearing using maximum kurtosis fast nonlocal means denoising,” Measurement, Vol. 100, pp. 157–163, Mar. 2017, https://doi.org/10.1016/j.measurement.2016.12.058
-
K. Xue, Z. Wu, H. Li, and G. Yang, “Research on identification method of aero-engine bearing fault using acoustic emission technique based on wavelet packet and rough set,” in 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), pp. 1499–1503, Mar. 2017, https://doi.org/10.1109/iaeac.2017.8054263
-
F. Guo, S. Shen, Z. Duan, Z. Fan, and Z. Sun, “Acoustic emission fault diagnosis of rolling bearing based on discrete hidden Markov model,” in Springer Proceedings in Physics, Vol. 14, No. 6, pp. 379–386, 2019, https://doi.org/10.1007/978-3-030-12111-2_35
-
H. Li, Z. Wu, K. Xue, and G. Yang, “Research on aero-engine bearing fault using acoustic emission technique based on wavelet packet decomposition and support vector machine,” in 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), pp. 1444–1448, Mar. 2017, https://doi.org/10.1109/iaeac.2017.8054252
-
J. Singh, A. K. Darpe, and S. P. Singh, “Rolling element bearing fault diagnosis based on Over-Complete rational dilation wavelet transform and auto-correlation of analytic energy operator,” Mechanical Systems and Signal Processing, Vol. 100, pp. 662–693, Feb. 2018, https://doi.org/10.1016/j.ymssp.2017.06.040
-
L. Cui, B. Li, J. Ma, and Z. Jin, “Quantitative trend fault diagnosis of a rolling bearing based on Sparsogram and Lempel-Ziv,” Measurement, Vol. 128, pp. 410–418, Nov. 2018, https://doi.org/10.1016/j.measurement.2018.06.051
-
D. Zhang, M. Entezami, E. Stewart, C. Roberts, and D. Yu, “Adaptive fault feature extraction from wayside acoustic signals from train bearings,” Journal of Sound and Vibration, Vol. 425, pp. 221–238, Jul. 2018, https://doi.org/10.1016/j.jsv.2018.04.004
-
W. Huang, H. Sun, J. Luo, and W. Wang, “Periodic feature oriented adapted dictionary free OMP for rolling element bearing incipient fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 126, pp. 137–160, Jul. 2019, https://doi.org/10.1016/j.ymssp.2019.02.023
-
B. Chen et al., “Fault diagnosis method based on integration of RSSD and wavelet transform to rolling bearing,” Measurement, Vol. 131, pp. 400–411, Jan. 2019, https://doi.org/10.1016/j.measurement.2018.07.043
-
H. Zhao and W. Zhang, “Fault diagnosis method for rolling bearings based on segment tensor rank-(L, L, 1) decomposition,” Mechanical Systems and Signal Processing, Vol. 132, pp. 762–775, Oct. 2019, https://doi.org/10.1016/j.ymssp.2019.05.016
-
M. J. Hasan, M. M. M. Islam, and J.-M. Kim, “Acoustic spectral imaging and transfer learning for reliable bearing fault diagnosis under variable speed conditions,” Measurement, Vol. 138, pp. 620–631, May 2019, https://doi.org/10.1016/j.measurement.2019.02.075
-
A. Rohani Bastami, A. Aasi, and H. A. Arghand, “Estimation of remaining useful life of rolling element bearings using wavelet packet decomposition and artificial neural network,” Iranian Journal of Science and Technology, Transactions of Electrical Engineering, Vol. 43, No. S1, pp. 233–245, Jul. 2019, https://doi.org/10.1007/s40998-018-0108-y
-
K. Lu, T. Lin, J. Xue, J. Shang, and C. Ni, “An automated bearing fault diagnosis using a self-normalizing convolutional neural network,” in 2019 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), pp. 908–912, Aug. 2019, https://doi.org/10.1109/qr2mse46217.2019.9021151
-
H. O. Omoregbee and P. S. Heyns, “Fault classification of low-speed bearings based on support vector machine for regression and genetic algorithms using acoustic emission,” Journal of Vibration Engineering and Technologies, Vol. 7, No. 5, pp. 455–464, Oct. 2019, https://doi.org/10.1007/s42417-019-00143-y
-
R. S. Gunerkar and A. K. Jalan, “Classification of ball bearing faults using vibro-acoustic sensor data fusion,” Experimental Techniques, Vol. 43, No. 5, pp. 635–643, Oct. 2019, https://doi.org/10.1007/s40799-019-00324-0
-
D. Liu, J. Tao, A. Luo, and Q. Wang, “An optimized kurtogram method for early fault detection of rolling element bearings using acoustic emission,” in 2018 International Conference on Information Systems and Computer Aided Education (ICISCAE), pp. 365–370, Jul. 2018, https://doi.org/10.1109/iciscae.2018.8666929
-
S. R. Saufi, Z. A. B. Ahmad, M. S. Leong, and M. H. Lim, “Low-speed bearing fault diagnosis based on ArSSAE model using acoustic emission and vibration signals,” IEEE Access, Vol. 7, pp. 46885–46897, 2019, https://doi.org/10.1109/access.2019.2909756
-
W. Du et al., “A new fuzzy logic classifier based on multiscale permutation entropy and its application in bearing fault diagnosis,” Entropy, Vol. 22, No. 1, p. 27, Dec. 2019, https://doi.org/10.3390/e22010027
