Modified weak signal fault diagnosis method forbearing inner ring

Luo, Chenxu; Jing, Shuangxi; Yang, Xin; Yuan, Jinle

Vibroengineering Procedia

Browse Procedia

Published: 08 December 2016

Check for updates

Modified weak signal fault diagnosis method forbearing inner ring

Chenxu Luo¹

Shuangxi Jing²

Xin Yang³

Jinle Yuan⁴

^{1, 2, 3, 4}School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454000, China

Corresponding Author:

Chenxu Luo

Cite the article Download PDF

Downloads 1341

Abstract

In view of the shortcomings of mode mixing in EMD, the excess IMF component in the low frequency band, spectral kurtosis has no adaptive. The method of EMD and spectral kurtosis are proposed. Spectral kurtosis is very sensitive to the fault signal and it can enhance the fault pulse signal effectively. Then combine spectral kurtosis with EMD to overcome the shortcomings of EMD. Improved the efficiency and accuracy of EMD decomposition and the level of fault diagnosis. The method of EMD and spectral kurtosis are applied to the simulation signal and rolling bearing fault diagnosis. The experimental results show that the method of EMD and spectrum kurtosis can accurately judge the rolling bearing weak fault and have a good application prospect.

1. Introduction

Rolling bearing is widely used in various industrial field, it will affect the operation of the whole machine’s function directly. Therefore, it has very important significance for early fault diagnosis. In the early stage of the rolling bearing, the weak impact component is not obvious, which is often submerged in the noise signal. It can reduce the noise and improve the signal-to-noise ratio effectively, this is the key to rolling bearing weak fault diagnosis.

The time-frequency of Empirical Mode Decomposition (EMD) analysis method is an excellent time-frequency signal analysis method. It is belong to a method of the adaptive time-frequency analysis, and was first proposed by the United States National Aeronautics and Space Administration's Huang. EMD method has a wide application field. Wuhan University of Science and Technology had applied this method to the classification of the damage form of refractories, thus realizing the damage pattern recognition of refractory materials [1]. Spectral kurtosis, which was created to overcome the shortcomings of the power spectral density in the local analysis, is a method proposed by Dwyer [2] and it can better detect the transient characteristics of the signal. The essence of this method is to find the frequency contained in the signal characteristics by detecting the non-stationarity of the signal on each line. Antoni [3] used the Wold-Cramer decomposition to normalize the spectral kurtosis method and proposed a kurtogram (Kurtogram), which is a fast algorithm for spectral kurtosis [4]. It had applied to the fault diagnosis and achieved a good result.

2. Vibration mechanism and fault diagnosis theory of rolling bearings

2.1. Vibration mechanism of rolling bearing

The modeling of rolling bearing fault signal is the basis of fault diagnosis. The accuracy of the model will directly affect the fault diagnosis application fault diagnosis of rolling bearing. There are many kinds of simulation models of bearing fault signals. Among them, the bearing fault signal model established by Macfadden is a good vibration characteristics indicator of rolling bearing faults. The period of the impact is defined as $T$ , the natural frequency oscillation function of the shock is $s (t)$ , and the amplitude of the $k$ times impulse response is $A_{k}$ . The working environment of rolling bearing is relatively bad, so there is often exist interference of additive noise $n (t)$ during its operation. Therefore, the rolling bearing surface damage failure vibration mathematical model established by Menacfadd can be described as:

1

f (t) = \sum_{k = \infty}^{+ \infty} A_{k} s (t - k T) U (t - k T) + n (t) .

In the formula: $U (t)$ is the unit step function; According to the theory of mechanical vibration, natural frequency vibration is usually a damp free vibration attenuation, so the vibration function $s (t)$ is related to the bearing’s natural frequency $f_{n}$ and damping ratio $ξ$ , thus it can be simplified as an exponentially decaying sinusoidal signal, as follows shows:

2

s (t) = \exp (\frac{ξ}{1 - ξ^{2}} 2 π f_{n} t) \sin [2 π f_{n} t + \emptyset] .

In the formula: $Φ$ is the initial phase; the damping ratio $ξ$ of the system must be chosen carefully, so that it can simulate the decay process of the vibration waveform and ensure $s (t)$ is always almost zero outside $[0, T]$ , and it is in order to avoid the interference between the two shock oscillations.

When the rotation period of the absolute position of the damage fault is greater than the period of the impact generation, the magnitude of the impulse response will also be modulated, at which time $A_{k}$ can be expressed as:

3

A_{k} = a_{k} \cos (2 π f_{m} t + \emptyset) + c_{k} .

In the formula: $a_{k}$ is the $k$ th impact energy, $Ф$ is the initial phase, $f_{m}$ is the modulation frequency (Outer ring failure: $f_{m} =$ 0; inner ring failure: $f_{m} = f_{r}$ ; rolling body failure: $f_{m} = f_{c}$ ). Since the magnitude of each shock is not always equal and always with a certain randomness, so the introduction of random constant $c_{k}$ .

According to Eqs. (1), (2) and (3), the characteristic frequency of the fault rolling bearing is related to the contact angle of rolling element. As the bearing speed fluctuations and the different location of the rolling body in the bearing area all will change the rolling contact angle between the rolling element and the raceway, so resulting in the different speed of the bearing of the rolling. The role of the cage makes the revolution of the rolling body to maintain the same speed, this will inevitably lead to a small slip between the rolling and the formation, so produce a minor change of the impact of the oscillation cycle. Considering the factor of the rolling element sliding, the time fluctuation of the $k$ times impact interval relative to the impact repetition period $T$ is $τ_{k}$ . Therefore, the mathematical model of rolling bearing damage type vibration can be expressed as:

4

f (t) = \sum_{k = - \infty}^{+ \infty} A_{k} s (t - k T - τ_{k}) U (t - k T - τ_{k}) + n (t),

A_{k} = a_{k} \cos (2 π f_{m} t + \emptyset) + c_{k},

s (t - k T - τ_{k}) = \exp (\frac{ξ}{1 - ξ^{2}} 2 π f_{n} (t - k T - τ_{k}) \sin [2 π f_{n} (t - k T - τ_{k}) + \emptyset] .

2.2. The fault diagnosis method based on EMD and spectral kurtosis

Based on the characteristics of EMD and spectral kurtosis, which the foemer can adaptive noise reduction spectral and the later can optimal band-pass filter, a method of an EMD and spectral kurtosis fault diagnosis for rolling bearing is proposed, this method can be applied to extracted the fault feature of rolling bearing, and the transient shock component in the signal can be extracted in the strong background noise, so as to diagnose the weak fault type of the rolling bearing. In this paper, EMD and spectral kurtosis method were used to analyze the collected data:

1) Mutual correlation, mutual information and kurtosis index are used to eliminate the false components produced by EMD decomposition, that is the IMF will retained when the mutual information and cross-correlation coefficient of the original signal and the IMF component is big, smaller is considered to be false components and given to remove, the kurtosis of each IMF is different, retention kurtosis values which are greater, rejected the kurtosis value which are smaller. According to the above principles, we will select the larger value from the three groups of indicators to reconstructed signal.

2) The spectral kurtosis of the reconstructed signal can be defined by the Wold-Cramer decomposition of the nonstationary process, and the signal $y (t)$ is defined as:

5

y (t) = \int_{- \infty}^{+ \infty} e^{j 2 π f t} H (t, f) d X (f) .

In the formula, $H (t, f)$ is the complex envelope of signal $y (t)$ at time $t$ and frequency $f$ ; $X (f)$ is the spectrum of strictly white noise. The 2nd moments of the complex envelope can be defined as:

6

S_{2 n y} (f) = E \{{|H (t, f) d X (f)|}^{2 n}\} / d f = E \{{|H (t, f)|}^{2 n}\} • S_{2 n X} .

In the formula, $E ()$ is the mathematical expectation; $n \in Z$ ; $S_{2 n X}$ is the 2 $n$ moment of $X (f)$ .

By the above definition, the fourth moment $C_{4 y} (f)$ of the complex envelope of $y (t)$ can be defined as:

7

C_{4 y} (f) = S_{4 y} (f) - 2 S_{2 y}^{2} (f), f \neq 0 .

The fourth-order moment of the energy normalization gives a measure of the probability density function at the frequency $f$ , which defines the spectral kurtosis:

8

K {}_{y} (f) = \frac{C_{4 y} (f)}{S_{2 y}^{2} (f)} = \frac{S_{4 y} (f)}{S_{2 y}^{2} (f)} - 2, f \neq 0 .

The optimal band-pass filter of the reconstructed signal is designed and filtered. Finally, the filtered signal is analyzed by envelope demodulation to get the purpose of extracting the characteristic frequency of the fault.

3. Experimental design

In this paper, we use the powertrain fault diagnosis comprehensive test bed, which developed by SpectraQuest, to test the weak inner and outer rings fault of rolling bearing, and to verificat the Superior of the method, which is combination by EMD and Spectral Kurtosis for Feature Extraction of Rolling Bearing Faults. Powertrain fault diagnosis comprehensive experimental platform consist of speed drive motors, torque sensors, encoders, a planetary gear box, two parallel shaft gear box, programmable magnetic brakes and data acquisition system. The synthetic test bed can simulate the failure, produced in the inner ring and the outer ring of the rolling bearing respectively, and collect the corresponding fault signal through the acceleration sensor installed on the fault bearing end cover.

As shown test in Fig. 1, the test Drive System use MB ER16K deep groove ball bearings, inner diameter is 25.4 mm, outer diameter is 51 mm, pitch diameter is 38 mm, the number of rolling is 9, the rolling body diameter is 8 mm, contact angle is 0°, and in each experiment, only a single failure of the rolling bearing is analyzed. According to the rolling bearing fault characteristic frequency formula of the previous chapter: $f_{o} = 3.5 f_{r}$ , $f_{i} = 5.4 f_{r}$ , in the part $f_{r}$ is the shaft frequency of the bearing. In this paper, the vibration characteristics of the rolling bearing are studied under the condition that the motor rotation frequency $f_{ε}$ is 45 Hz, 55 Hz, the planetary gearbox reduction ratio is 4.57, the ratio of parallel gearbox reduction are 8.62, Planetary gear box meshing frequency $f_{g}$ are respectively 975 Hz and 1203 Hz, parallel gearbox input shaft frequency ${f_{r}}_{1}$ are respectively 9.7 Hz and 12 Hz (carrier frequency), the intermediate shaft frequency ${f_{r}}_{2}$ are respectively 2.8 Hz and 3.5 Hz, the output shaft frequency ${f_{r}}_{3}$ are respectively 1.13 Hz and 1.4 Hz; The meshing frequencies ${f_{m}}_{1}$ of the parallel gearboxes are 282.4 Hz and 348.3 Hz, the secondary meshing frequencies $f_{m 2}$ are 102 Hz and 125.6 Hz; when the motor frequency 45 Hz, the Rolling bearing inner ring fault frequency is 15.3 Hz, and when the motor frequency 55 Hz, the inner ring fault frequency 18.9 Hz.

Fig. 1The diagram of the gear transmission

4. The data analysis of Roller bearing inner ring failure experimental

4.1. Inner ring fault, the motor frequency 45 Hz, parallel gear box radial load 1570 N

Take the single-point fault rolling bearing, install it on the gearbox intermediate shaft, adjust the radial load of the gearbox to 1570 N and set the sampling frequency of the sampling system 12.8 kHz, and then collect the vibration signal of the rolling bearing. Only analysis the vertical vibration signal acquired by the sensor 1. The time domain waveform of the signal acquired by the sensor is shown in Fig. 2. It can be seen that the periodic impact component in the signal is not obvious due to the influence of other interfering noise. Fig. 3 is the amplitude of the vibration signal spectrum, which is obtained by the sensor 1, in the figure we can see that the main frequency components is 1 $f_{e}$ frequency (44.8 Hz), 3 times the frequency of 3 $f_{e}$ (134.4 Hz) of the motor frequency, and 2 times the frequency of 2 $f_{e}$ (1950 Hz), 3 times the frequency of 3 (2930 Hz), 4 times the frequency of 4 (3900 Hz) of parallel gear box frequency. It has been observed that the side bands on both sides of the parallel gearbox meshing frequency 2 octave 2 (564.8 Hz) are very weak, so the gears in the parallel case are not faulty and conform to the actual situation. The interval of them, which is the meshing frequency $f_{g}$ (975 Hz) of planetary box and a large number of sidebands existence on both sides of multi frequency, are the rotation frequency ${f_{r}}_{1}$ of the planet carrier (9.7 Hz), 2 ${f_{r}}_{1}$ (19.4 Hz) and multi frequency doubling, the partial enlargement as shown in Fig. 4, this is a characteristic of normal planetary gear box show. It is very difficult to extract the fault feature only base on the amplitude spectrum of the fault signal.

Fig. 5 shows the direct envelope spectrum of the inner ring vibration signal, it can be seen that the fault inner ring frequency of the rolling bearing, which contain 1 time frequency $f_{i}$ (15.3 Hz), 2 times of frequency 2 $f_{i}$ (30.6 Hz), 3 times of frequency 3 $f_{i}$ (46 Hz), cannot be accurately extracted because the effects of noise and complex low-frequency modulation phenomena. In this figure, only parallel gearbox input shaft frequency ${f_{r}}_{1}$ (9.7 Hz), the middle shaft frequency ${f_{r}}_{2}$ (2.8 Hz), the motor frequency $f_{e}$ (44.8 Hz) are more obvious. The inner fault signal is analyzed by using the method mentioned in this paper, and the EMD algorithm is used to decompose the 17 IMF components of the inner fault signal, calculate the cross-correlation, mutual information between the original signal and with the individual components, and the kurtosis values of the individual components. As there are so much components, the paper only gives the former six components of the cross-correlation (0.6, 0.4, 0.6, 0.3, 0.1, 0.03), mutual information (0.3, 0.2, 0.3, 0.2, 0.1, 0.1) and kurtosis value (3.6, 7.4, 4.7, 3.6, 4.0, 3.2). The first two sets of IMF component are used to reconstruction signal, and the rest of the component as a false component to give out.

Fig. 2Time domain waveform of vibration signal

Fig. 3Amplitude spectrum of vibration signal

Fig. 4Local amplification figure of amplitude spectrum of vibration signal

Fig. 5Direct envelope spectrum of vibration signal

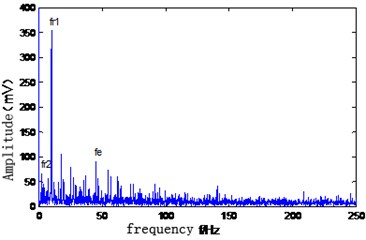
Fig. 6Kurtogram of reconstructed signal

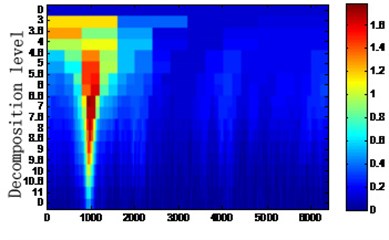
Fig. 7Envelope spectrum after filtering

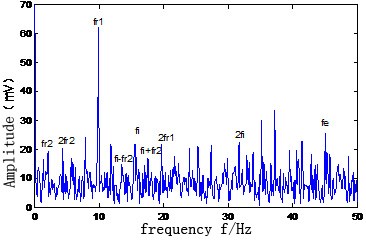
Fig. 6 shows the spectral kurtosis of the reconstructed signal. Fig. 6 shows the maximum kurtosis of the fault signal is 950 Hz produced in the center frequency of 1.8 corresponds, and the filter frequency band is [500, 1200] Hz. The reconstructed signal is filtered by the band-pass filter, and the filtered signal is subjected to envelope analysis. The envelope spectrum of the reconstructed signal is shown in Fig. 7. The main frequency components of the reconstructed signal are frequency 1 octave ${f_{r}}_{2}$ (2.8 Hz), 2nd octave 2 ${f_{r}}_{2}$ (5.6 Hz) of parallel gearbox intermediate axis;1 time the frequency ${f_{r}}_{1}$ (9.7 Hz), 2 times the frequency 2 ${f_{r}}_{1}$ (19.4 Hz) of Input shaft frequency, 1 time frequency $f_{i}$ (15.3 Hz), 2 times frequency 2 $f_{i}$ (30.6 Hz) of the bearing inner ring failure ,and the motor frequency (44.8 Hz). And there is a modulation side frequency, which with the fault bearing axis as the interval, band on both sides of the failure frequency of the inner ring. The results show: EMD and spectral kurtosis method is overcome the mode aliasing interference, use the sensitivity of spectral kurtosis of the fault pulse signal (spectral kurtosis have this advantage) to accurately extract the weak characteristics of the frequency of fault in the inner bearing. Comparing Fig. 5, the method overcomes some shortcomings of the traditional envelope analysis method, and has certain superiority and practicability.

5. Conclusions

Through the analysis of the frequency characteristics of rolling bearings under different fault types, so that to verify combined method of the EMD and spectral kurtosis with the validity and superiority. Experimental results show: EMD and spectral kurtosis method can effectively remove the interference signal, Highlighting the cyclical impact component of the fault signal, the validity and practicability of the method are verified in the weak fault diagnosis of rolling bearing, and provides an effective basis for the study of rolling bearing faults.

References

Li Jinwei, Wang Qi, He Taihong, et al. Based on EMD and ELM fires speed transmission line combination forecast model. Journal of Spread Power Construction, Vol. 36, Issue 3, 2015, p. 27-31.

Search CrossRef
Antoni J. The spectral kurtosis: a useful tool for characterizing non-stationary signals. Journal of Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 282-307.

Search CrossRef
Antoni J. Fast computation of the kurtogram for the detection of transient faults. Journal of Mechanical Systems and Signal Processing, Vol. 20, 2007, p. 108-124.

Search CrossRef
Ren Xueping, Pang Zhen, Xin Xiangzhi Application of wavelet packet and kurtosis in early fault analysis of bearings. Journal Bearings, Vol. 3, 2014.

Search CrossRef
Wu Zhaotong, Yang Shixi New Method for Rotating Machinery Fault Feature Extraction and Pattern Classification. Science Press, 2012, p. 60-63.

Search CrossRef
Jiang Qiongfei, Guo Shengli, Liang Haowen, et al. Interdecadal variability of East Asian summer monsoon and its relationship with solar activity based on EMD. Journal of Space Science, Vol. 35, Issue 1, 2015, p. 50-55.

Search CrossRef
Dwyer R. F. Detection of non-Gaussian signals by frequency domain kurtosis estimation. International Conference on Acoustics, Speech, and Signal Processing, Boston, USA, 1983, p. 607-610.

Search CrossRef
Jinwei Shen, Linsuo Shi An improved wavelet transform spectral kurtosis method for fault diagnosis of rolling bearings. Journal Bearings, Vol. 8, 2010.

Search CrossRef
Dai Haomin, Xu Aiqiang, Li Wenfeng, et al. Application of spectrum kurtosis method based on EMD in fault diagnosis of rolling bearing. Journal of Computer Measurement and Control, Vol. 3, 2015.

Search CrossRef
Liu Weiting Fault Feature Extraction of Gearbox Based on Spectrum Kurtosis. D. Kunming University of Science and Technology, 2011.

Search CrossRef
Zheng Wei, Fan K. Q. Vibration source monitoring method based on uncertainty of spectrum kurtosis. Journal of Noise and Vibration Control, Vol. 5, 2007, p. 94-96.

Search CrossRef
Zhu Ling, Liu Zhigang, Hu Qiaolin Based on the spectral kurtosis CWD transient power quality disturbance identification. Journal of Electric Power Automation Equipment, Vol. 34, Issue 2, 2014, p. 125-132.

Search CrossRef

About this article

Received

08 November 2016

Accepted

09 November 2016

Published

08 December 2016

SUBJECTS

Fault diagnosis based on vibration signal analysis

Keywords

EMD

spectral kurtosis

fault diagnosis

rolling bearing

feature extraction

Acknowledgements

The authors are grateful for the funding of this work by the Henan Province Education Department Applied Research Project Fund (16A460005) and Henan Polytechnic University Doctor Research Project Fund (660407/020) and China Postdoctoral Science Foundation Funded Project (Project No. 2016M592289).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.