The semi-analytical method for damping of tubular transition layer damping structure

Zhang, Wenjun; Sun, Dagang; Yan, Bijuan; Li, Zhanlong; Liu, Shizhong

doi:10.21595/jve.2017.18172

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2018

Check for updates

The semi-analytical method for damping of tubular transition layer damping structure

Wenjun Zhang¹

Dagang Sun²

Bijuan Yan³

Zhanlong Li⁴

Shizhong Liu⁵

^{1, 2, 3, 4}Mechanical Engineering College, Taiyuan University of Science and Technology, Taiyuan, China

^{5, 1}Transportation and Logistics College, Taiyuan University of Science and Technology, Taiyuan, China

Corresponding Author:

Dagang Sun

Cite the article Download PDF

Downloads 1463

WoS Core Citations 1

CrossRef Citations 1

Abstract

To solve the limited vibration consumption of the traditional tubular damping structure (TTDS), the tubular transition layer damping structure (TTLDS) is proposed; Based on viscoelastic materials and theories of thin cylindrical shells, the governing equation, the first order matrix differential equation describing vibration of TTLDS under harmonic excitation, is derived by considering the interaction between all layers and the dissipation caused by the shear deformation for transition layer and damping layer. By using the extended homogeneous capacity precision integration method to solve the control equation, a semi-analytical method for studying the vibration and damping characteristics of TTLDS is given. By way of comparison, the correctness of the method provided in paper is verified. At last, the influence of thickness, material and location of transition layer on damping effect is analyzed. The results show that the change for the thickness or material of the transition layer can make the structural damping effect change greatly, while the change for location of the transition layer plays only a few roles on the structural damping effect.

1. Introduction

The Tubular structure has a good carrying capacity and can meet those requirements not only with enough stiffness and strength but also with a lighter weight. It is widely used in aerospace engineering, marine and offshore engineering, civil construction, machinery equipment and nuclear industry fields. During its use, the tubular structure produces resonance and instability under the effect of the vibration, shock, wind load, seismic and other dynamic load, which leads to failure of the equipment or facilities and damage of property or people. To avoid the disadvantages mentioned above, the tubular structure can be treated by adding damping layer and constrained layer on its body to form traditional tubular damping structure (TTDS).

Many scholars have studied the damping effect of this damping structure: M. G. Sainsbury [1] analyzed the tubular damping structure which covered constrained layer partially through FEM and discussed the influence of different covering location on damping effect by using modal energy density map. Yu Xiang et al. [2] analyzed the vibration of PCLD tubular structure through a new matrix method, which covered damping layer partially, and discussed the frequency response for changing the coverage percentage and location of PCLD. Xiong-tao Cao et al. [3] studied the free vibration characteristics of passive tubular damping structure and solved the vibration equation of PCLD tubular structure simply supported at both ends by using wave propagation method. Cheng-feng Liu et al. [4] conducted topological optimization analysis and experimental research on the tubular damping structure by using evolutionary structural optimization; Being aimed at the vibration characteristics, Hui-rong Shi et al. [5] gave the local tubular damping structure model, analyzed the vibration characteristics and optimized it; Tai-hong Chen et al. [6] analyzed the damping effect of aluminum tube with a constrained damping layer by using layer by layer displacement theory. They compared the natural frequency, modal loss factor and frequency response of the damping tube with the original one and drew the conclusion that the constrained damping tubular structure could reduce vibration effectively. Based on the theory of Flügge shell, Mei-xia Chen et al. [7] established mathematical model of multi-cabin reinforcement tubular damping structure on arbitrary boundary conditions and studied its natural vibration and frequency response characteristics. Aimed at isolating the inner machinery vibration question of tubular structure, Xiao-le Wang et al. [8] gave an analytical fluctuation model for isolation vibration system of tubular damping structure and verified its effectiveness through FEM. Although traditional tubular damping structure (TTDS) can reduce the vibration energy, it is difficult to arrive at satisfactory effects in practice. In order to further improve the structure damping effect, some scholars have proposed another type tubular structure which is called tubular transition layer damping structure (TTLDS, see in Fig. 1(a)). It adds one more layer, which is called transition layer between base layer and damping layer of TTDS to form four-layer structure, and its material property lies in between metal material and rubber material. For the transition layer adding the distance between damping layer and base layer and levering the shear deformation of damping layer, the TTLDS can get a better damping effect than TTDS [9]. Some scholars have done research on four-layer damping structure: Jessica M. Yellin et al. [10] built a passive constrained four-layer beam model. They gave the kinematic equations and verified the results by related tests. Based on the FEM and ANSYS, Zhao-you Wei et al. [11] built a constrained damping beam with a slot strand-off layer and made modal analysis. Hui-rong Shi et al. [12] optimized the design of constrained damping beam with a transition layer under the help of FEM. They analyzed and compared the vibration characteristics with a continuous or discontinuous constrained layer respectively. A. W. V. Vuure et al. [13] applied strain energy method to predict damping effect of the multi-layer structure. Under knowing the loss factors of all layers, the multi-layer damping effect could be predicted by computing the distribution of stain energy with ANASYS. Sanjiv Kumar et al. [14] gave the kinematics equations of constrained damping structure with an active transition layer by adopting Hamilton principle and FEM. Cai-you Zhao et al. [15] applied the transition layer to damp the train tracks. They modeled the constrained damping structure with a slot transition layer and carried out related test. Through using simple proportional feedback control strategy, they gave out the numerical solution of complex eigenvalue for kinematics equations. Ravish S. Mastic et al. [16] analyzed the vibration characteristics of TTLDS which covered constrained layer partially through FEM. By using strain energy distribution map, they discussed the effect of location and size on vibration damping for constrained layer. After a review of relevant literatures, it can be seen that most of the present methods for research on transition layer are focused on plate structure, and a few of them on tubular structure with FEM.

To study the dynamic features of TTLDS, the first order ordinary differential equation is derived by considering the basic control equation of vibration and energy dissipation of viscoelastic damping layer and transition layer, as well as the interaction between these layers. Additionally, the damping characteristics are also analyzed through using the method of extend homogeneous capacity precision integration [17] to solve the ordinary differential equation.

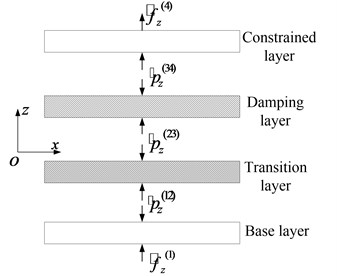
Fig. 1Tubular transitional layer damping structure: 1. base layer, 2. transition layer, 3. damping layer, 4. constrained layer

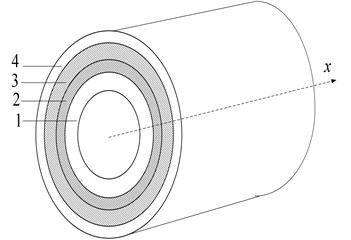
a) B-T-D-C

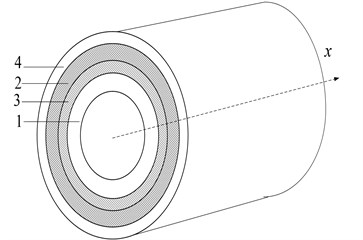
b) B-D-T-C

2. The governing equation of TTLDS

For simplicity, the following assumptions are made like Refs. [18-20]:

1) The radial displacement is same for these four layers, and the radial strain is negligible.

2) There is no slip at the interfaces between layers; that is, perfect continuity.

3) The transverse shear deformation is neglected except in transition layer and damping layer.

4) The bending deformations of base layer and constrained layer are consistent with the Kirchhoff ’s hypothesis.

5) The effect of rotary inertia of each layer is also neglected.

6) Only the radial vibration inertia is considered for transition layer and damping layer.

2.1. Shear deformation and shear force in transition layer and damping layer

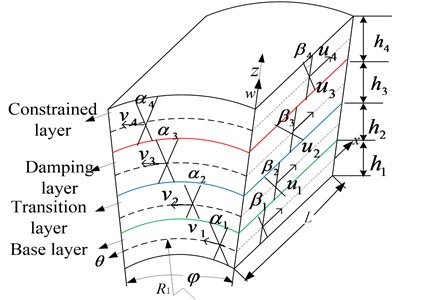
Now, a micro unit of TTLDS is cut out for analyzing. The micro unit is shown in Fig. 2, where $x$ represents axial direction; $θ$ represents peripheral; $z$ represents radial direction; $φ$ is peripheral dimensions $(°)$ ; $L$ is axial dimensions, $m$ ; $h_{i}$ is the thickness of $i$ th layer. $u_{i}$ , $v_{i}$ , $w_{i}$ ( $i =$ 1, 2, 3, 4) denote the displacement amplitudes in $x$ , $θ$ , $z$ -direction at the mid-plane of $i$ th layer, $m$ ; $β_{i}$ and $α_{i}$ ( $i =$ 1, 2, 3, 4) denote the rotations in $x$ and $θ$ -direction, respectively $(°)$ ; $R_{i}$ ( $i =$ 1, 2, 3, 4) is radius of $i$ th layer, $m$ ;

From the deformation coordination of Fig. 2, the amplitudes of mid-plane displacement and rotation of the cross-section in $x$ and $θ$ -direction in transition layer can be expressed as:

1

\{\begin{array}{l} u_{2} (x, θ) = \frac{1}{2} ((u_{1} (x, θ) + \frac{h_{1}}{2} β_{1} (x, θ)) + (u_{3} (x, θ) - \frac{h_{3}}{2} β_{3} (x, θ))), \\ β_{2} (x, θ) = \frac{1}{h_{2}} ((u_{3} (x, θ) - \frac{h_{3}}{2} β_{3} (x, θ)) - (u_{1} (x, θ) + \frac{h_{1}}{2} β_{1} (x, θ))), \end{array}

2

\{\begin{array}{l} v_{2} (x, θ) = \frac{1}{2} ((v_{1} (x, θ) + \frac{h_{1}}{2} α_{1} (x, θ)) + (v_{3} (x, θ) - \frac{h_{3}}{2} α_{3} (x, θ))), \\ α_{2} (x, θ) = \frac{1}{h_{2}} ((v_{3} (x, θ) - \frac{h_{3}}{2} α_{3} (x, θ)) - (v_{1} (x, θ) + \frac{h_{1}}{2} α_{1} (x, θ))) . \end{array}

Fig. 2Micro-unit of TTLDS

The amplitudes of mid-plane displacement and rotation of the cross-section in $x$ and $θ$ -direction in damping layer can be expressed by:

3

\{\begin{array}{l} u_{3} (x, θ) = \frac{1}{2} ((u_{2} (x, θ) + \frac{h_{2}}{2} β_{2} (x, θ)) + (u_{4} (x, θ) - \frac{h_{4}}{2} β_{4} (x, θ))), \\ β_{3} (x, θ) = \frac{1}{h_{3}} ((u_{4} (x, θ) - \frac{h_{4}}{2} β_{4} (x, θ)) - (u_{2} (x, θ) + \frac{h_{2}}{2} β_{2} (x, θ))), \end{array}

4

\{\begin{array}{l} v_{3} (x, θ) = \frac{1}{2} ((v_{2} (x, θ) + \frac{h_{2}}{2} α_{2} (x, θ)) + (v_{4} (x, θ) - \frac{h_{4}}{2} α_{4} (x, θ))), \\ α_{3} (x, θ) = \frac{1}{h_{3}} ((v_{4} (x, θ) - \frac{h_{4}}{2} α_{4} (x, θ)) - (v_{2} (x, θ) + \frac{h_{2}}{2} α_{2} (x, θ))) . \end{array}

Applying Kirchhoff’s hypothesis and the cylindrical shell theory to base layer and constrained layer, the following equation can be written as:

5

β_{i} = - \frac{\partial w}{\partial x} = β, α_{i} = \frac{1}{R_{i}} (v_{i} - \frac{\partial w}{\partial θ}) = \frac{1}{R_{i}} (v_{i} - α), (i = 1, 4) .

Adopting the first-order shear deformation model, the displacement of an arbitrary point in the thickness direction for transition layer and damping layer can be written by:

6

\{\begin{array}{l} u_{i} (x, θ, z) = u_{i} (x, θ) + h_{i} β_{i} (x, θ), \\ v_{i} (x, θ, z) = v_{i} (x, θ) + h_{i} α_{i} (x, θ), \\ w (x, θ, z) = w (x, θ) . \end{array} (i = 2, 3) .

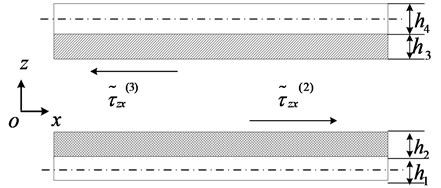
According to shear force balance in $x$ and $θ$ -direction showed in Fig. 3, the following equations can be obtained:

7

G_{2} {γ_{z x}}^{(2)} = G_{3} {γ_{z x}}^{(3)},

8

G_{2} {γ_{z θ}}^{(2)} = G_{3} {γ_{z θ}}^{(3)},

where $G_{2}$ is the shear modulus of transition layer well $G_{3}$ is damping layer; $γ_{z x}^{(2)}$ and $γ_{z θ}^{(2)}$ are shear deformation amplitudes for transition layer in $x$ and $θ$ -direction; $γ_{z x}^{(3)}$ and $γ_{z θ}^{(3)}$ are shear deformation amplitude for damping layer in $x$ and $θ$ -direction.

Fig. 3The schematic of shear force balance

Being simultaneous Eqs. (7), (8), (1) and (2), the mid-plane displacement and rotation of the cross-section for transition layer in $x$ and $θ$ -direction can be expressed as:

9

\{\begin{array}{l} u_{2} (x, θ) = \frac{1}{4 (G_{3} h_{2} + G_{2} h_{3})} (\begin{matrix} (4 G_{2} h_{3} + 2 G_{3} h_{2}) u_{1} + 2 G_{3} h_{2} u_{4} \\ + (2 h_{2} h_{3} (G_{2} - G_{3}) + G_{3} h_{2} (h_{1} - h_{4}) + 2 G_{2} h_{1} h_{3}) β \end{matrix}), \\ β_{2} (x, θ) = \frac{1}{2 (G_{3} h_{2} + G_{2} h_{3})} (- 2 G_{3} u_{1} + 2 G_{3} u_{4} + (2 h_{3} (G_{2} - G_{3}) - G_{3} (h_{1} + h_{4})) β), \end{array}

10

\{\begin{array}{l} v_{2} (x, θ) = \frac{1}{4 g} (\begin{matrix} a R_{2} R_{4} v_{1} (4 G_{3} R_{2} R_{3} h_{3} + 2 G_{3} R_{3} h_{2} + G_{3} h_{2} h_{3}) + b h_{2} v_{4} \\ + ((c - d) G_{3} R_{2} h_{2} - 4 G_{2} R_{3} R_{4} h_{3} (R_{1} h_{2} + R_{2} h_{1})) α \end{matrix}), \\ α_{2} (x, θ) = \frac{1}{2 g} (\begin{matrix} a (2 G_{2} R_{3} h_{3} - 2 G_{3} R_{2} R_{3} - G_{3} R_{2} h_{3}) R_{4} v_{1} \\ + b v_{4} + (G_{3} R_{2} (c + d) - 2 a G_{2} R_{3} R_{4} h_{3}) α \end{matrix}), \end{array}

where:

\begin{array}{l} a = 2 R_{1} + h_{1}, b = (2 R_{4} - h_{4}) (2 R_{3} - h_{3}) G_{3} R_{1} R_{2}, \\ c = 2 R_{1} R_{3} h_{4} + 4 R_{1} R_{4} h_{3} - R_{1} h_{3} h_{4}, d = 2 R_{3} R_{4} h_{1} + R_{4} h_{1} h_{3}, \\ g = G_{2} R_{1} R_{4} R_{3} h_{3} (2 R_{2} - h_{2}) + G_{3} R_{1} R_{4} R_{2} h_{2} (2 R_{3} + h_{3}) . \end{array}

Being simultaneous Eqs. (7), (8), (3) and (4), the mid-plane displacement and rotation of the cross-section for damping layer in $x$ and $θ$ -direction can be expressed as:

11

\{\begin{array}{l} u_{3} (x, θ) = \frac{1}{4 (G_{3} h_{2} + G_{2} h_{3})} (\begin{matrix} 2 G_{2} h_{3} u_{1} + (4 G_{3} h_{^{2}} + 2 G_{2} h_{3}) u_{4} \\ + (2 h_{2} h_{3} (G_{2} - G_{3}) + G_{2} h_{3} (h_{1} - h_{4}) - 2 G_{3} h_{2} h_{4}) β \end{matrix}), \\ β_{3} (x, θ) = - \frac{1}{2 (G_{3} h_{2} + G_{2} h_{3})} (2 G_{2} u_{1} - 2 G_{2} u_{4} + (2 h_{2} (G_{2} - G_{3}) + G_{2} (h_{1} + h_{4})) β), \end{array}

12

\{\begin{array}{l} v_{3} (x, θ) = \frac{1}{4 g} (\begin{matrix} b^{'} h_{3} v_{1} + a^{'} R_{3} v_{4} (4 G_{3} R_{2} h_{2} + 2 G_{2} R_{2} h_{3} - G_{2} h_{2} h_{3}) \\ + ((d^{'} - c^{'}) G_{2} R_{3} h_{3} + 4 G_{3} R_{1} R_{2} h_{2} (R_{3} h_{4} + R_{4} h_{3})) α \end{matrix}), \\ α_{3} (x, θ) = - \frac{1}{2 g} (\begin{matrix} b^{'} v_{1} - a^{'} (2 G_{2} R_{2} R_{3} + 2 G_{3} R_{2} h_{2} - G_{2} R_{3} h_{2}) v_{4} \\ + (2 a^{'} G_{3} R_{2} h_{2} - G_{2} R_{3} h_{3} (c^{'} + d^{'})) α \end{matrix}), \end{array}

where:

\begin{array}{l} a^{'} = (2 R_{4} - h_{4}) R_{1}, b^{'} = (2 R_{2} + h_{2}) (2 R_{1} + h_{1}) G_{2} R_{3} R_{4}, \\ c^{'} = 2 R_{2} R_{4} h_{1} + R_{4} h_{1} h_{2}, d^{'} = 2 R_{1} R_{2} h_{4} - 4 R_{1} R_{4} h_{2} - R_{1} h_{2} h_{4} . \end{array}

By substituting Eq. (6) into the strain-displacement relationship [21], the shear strains in transition layer and damping layer [22] can be written by:

13

{γ_{z x}}^{(2)} = β_{2} + β, {γ_{z θ}}^{(2)} = α_{2} - \frac{v_{2}}{R_{2}} + \frac{1}{R_{2}} α,

14

{γ_{z x}}^{(3)} = β_{3} + β, {γ_{z θ}}^{(3)} = α_{3} - \frac{v_{3}}{R_{3}} + \frac{1}{R_{3}} α .

Inserting Eqs. (5), (9) and (10) into Eq. (13) and applying the Hooke’s law, the amplitude of shear stress for transition layer in $x$ and $θ$ -direction can be obtained as follows:

15

\{\begin{array}{l} {τ^{(2)}}_{z x} = G_{2} {γ^{(2)}}_{z x} = \frac{G_{2}}{2 (G_{2} h_{3} + G_{3} h_{2})} (- 2 G_{3} u_{1} + 2 G_{3} u_{4} - G_{3} (2 h_{2} + 2 h_{3} + h_{1} + h_{4}) β), \\ {τ^{(2)}}_{z θ} = G_{2} {γ^{(2)}}_{z θ} = \frac{G_{2}}{4 g} (G_{3} (v_{1} e (2 R_{1} + h_{1}) - v_{4} f (2 R_{4} - h_{4}) - (h_{1} e + h_{4} f + I) α)) . \end{array}

Inserting Eqs. (5), (11) and (12) into Eq. (14) and applying the Hooke’s law, the amplitude of shear stress for damping layer in $x$ and $θ$ -direction can obtained as follows:

16

\{\begin{array}{l} {τ^{(3)}}_{z x} = G_{3} {γ^{(3)}}_{z x} = - \frac{G_{3}}{2 (G_{2} h_{3} + G_{3} h_{2})} (2 G_{2} u_{1} - 2 G_{2} u_{4} + G_{2} (2 h_{2} + 2 h_{3} + h_{1} + h_{4}) β), \\ {τ^{3}}_{z θ} = G_{3} {γ^{(3)}}_{z θ} = \frac{G_{3}}{4 g} (G_{2} (v_{1} e (2 R_{1} + h_{1}) - v_{4} f (2 R_{4} - h_{4}) - (h_{1} e + h_{4} f + I) α)), \end{array}

where:

\begin{array}{l} e = (2 R_{3} + h_{3}) (2 R_{2} + h_{2}) R_{4}, f = (2 R_{3} - h_{3}) (2 R_{2} - h_{2}) R_{1}, \\ I = 8 R_{1} R_{4} (R_{2} h_{3} + R_{3} h_{2}) . \end{array}

The shear stresses must be considered in discussing the equilibrium equations of the base layer and constrained layer.

2.2. Matrix differential equation of first order of state vector for base layer and constrained layer

Under harmonic excitation, the equilibrium equations for base layer and constrained layer can be written as:

17

\{\begin{array}{l} \frac{\partial {N_{x}}^{(i)}}{\partial x} + \frac{\partial {N_{θ x}}^{(i)}}{R_{i} \partial θ} + ρ_{i} h_{i} ω^{2} u_{i} + {p_{x}}^{(i)} = 0, \\ \frac{\partial {N_{x θ}}^{(i)}}{\partial x} + \frac{\partial {N_{θ}}^{(i)}}{R_{i} \partial θ} + \frac{\partial {Q_{θ}}^{(i)}}{R_{i}} + ρ_{i} h_{i} ω^{2} v_{i} + {p_{θ}}^{(i)} = 0, \\ \frac{\partial {Q_{x}}^{(i)}}{\partial x} + \frac{\partial {Q_{θ}}^{(i)}}{R_{i} \partial θ} - \frac{{N_{θ}}^{(i)}}{R_{i}} + ρ_{i} h_{i} ω^{2} v_{i} + {p_{z}}^{(i)} = 0, \\ \frac{\partial {M_{x θ}}^{(i)}}{\partial x} + \frac{\partial {M_{θ}}^{(i)}}{R_{i} \partial θ} - {Q_{θ}}^{(i)} = 0, \\ \frac{\partial {M_{x}}^{(i)}}{\partial x} + \frac{\partial {M_{θ}}^{(i)}}{R_{i} \partial θ} - {Q_{x}}^{(i)} = 0, \end{array} (i = 1, \dots, 4),

where $N_{x}^{(i)}$ , $N_{θ}^{(i)}$ , $N_{θ x}^{(i)}$ , $M_{x}^{(i)}$ , $M_{θ}^{(i)}$ , $Q_{x}^{(i)}$ and $Q_{θ}^{(i)}$ ( $i =$ 1,…,4) denote the amplitudes of the membrane internal force and the bending internal force in the unit length of the $i$ th layer, respectively; $ρ_{i}$ denotes mass density of $i$ th layer; $p_{x}^{(1)}$ , $p_{θ}^{(1)}$ and $p_{z}^{(1)}$ are the amplitudes of surface forces on the base layer which include the external excitation and the interaction forces between base layer and transition layer; $p_{x}^{(4)}$ , $p_{θ}^{(4)}$ and $p_{z}^{(4)}$ are the amplitudes of surface forces on constrained layer which include the external excitation and the interaction forces between damping layer and constrained layer; $ω$ denotes the natural frequency or angular frequency of external excitation.

According to Kelvin-Kirchhoff’s equivalent, the amplitudes of in-plane shear force and transverse shear force can be expressed by:

18

{S_{x}}^{(i)} = {N_{x θ}}^{(i)} + \frac{1}{R_{i}} {M_{x θ}}^{(i)}, {V_{x}}^{(i)} = {Q_{x}}^{(i)} + \frac{1}{R_{i}} \frac{\partial {M_{x θ}}^{(i)}}{\partial θ}, (i = 1, \dots, 4) .

Adopting Reissner model, the internal force-displacement relationship for base layer and constrained layer [21] can be written as:

19

\{\begin{array}{l} {N_{x}}^{(i)} = K^{(i)} (\frac{\partial u_{i}}{\partial x} + μ_{i} (\frac{\partial v_{i}}{R_{i} \partial θ} + \frac{w}{R_{i}})), \\ {N_{θ}}^{(i)} = K^{(i)} (\frac{\partial v_{i}}{R_{i} \partial θ} + \frac{w}{R_{i}} + μ_{i} \frac{\partial u_{i}}{\partial x}), \\ {N_{x θ}}^{(i)} = {N_{θ x}}^{(i)} = K^{(i)} (\frac{1 - μ_{i}}{2}) (\frac{\partial u_{i}}{R_{i} \partial θ} + \frac{\partial v_{i}}{\partial x}), \\ {M_{x}}^{(i)} = D^{(i)} (\frac{\partial β}{\partial x} + μ_{i} \frac{\partial α_{i}}{R_{i} \partial θ}), {M_{θ}}^{(i)} = D^{(i)} (μ_{i} \frac{\partial β}{\partial x} + \frac{\partial α_{i}}{R_{i} \partial θ}), \\ {M_{x θ}}^{(i)} = {M_{θ x}}^{(i)} = D^{(i)} (1 - μ_{i}) \frac{\partial α_{i}}{\partial x} = D^{(i)} (1 - μ_{i}) (\frac{\partial v_{i}}{\partial x} + \frac{\partial β}{\partial θ}), (i = 1, \dots, 4), \end{array}

where:

β = - \frac{\partial w}{\partial x}, α_{i} = \frac{1}{R_{i}} [v_{i} - \frac{\partial w}{\partial x}], K^{(i)} = \frac{E_{i} h_{i}}{1 - {μ_{i}}^{2}}, D^{(i)} = \frac{E_{i} {h_{i}}^{3}}{12 (1 - {μ_{i}}^{2})} .

Using Fourier expansions in the circumferential direction, the assumed distributions of the displacements and internal force in the $i$ th layer can be expressed as:

\{\begin{array}{l} (u_{i}, w) = L \sum_{n} ({\bar{u}}_{n}^{(i)}, {\bar{w}}_{n}) c o s (n θ), \\ v_{i} = L \sum_{n} {\bar{v}}_{n}^{(i)} s i n (n θ), \\ β = \sum_{n} {\bar{β}}_{n} c o s (n θ), \\ ({N_{x}}^{(i)}, {N_{θ}}^{(i)}, {Q_{x}}^{(i)}, {V_{x}}^{(i)}) = K^{(i)} \sum_{n} ({\bar{N}}_{x n}^{(i)}, {\bar{N}}_{θ n}^{(i)}, {\bar{Q}}_{x n}^{(i)}, {\bar{V}}_{x n}^{(i)}) c o s (n θ), \\ ({N_{x θ}}^{(i)}, {N_{θ x}}^{(i)}, {Q_{θ}}^{(i)}, {S_{x}}^{(i)}) = K^{(i)} \sum_{n} ({\bar{N}}_{x θ n}^{(i)}, {\bar{N}}_{θ x n}^{(i)}, {\bar{Q}}_{θ n}^{(i)}, {\bar{S}}_{x n}^{(i)}) s i n (n θ) \\ ({M_{x}}^{(i)}, {M_{θ}}^{(i)}) = (L K^{(i)}) \sum_{n} ({\bar{M}}_{x n}^{(i)}, {\bar{M}}_{θ n}^{(i)}) c o s (n θ), \\ ({M_{x θ}}^{(i)}, {M_{θ x}}^{(i)}) = (L K^{(i)}) \sum_{n} ({\bar{M}}_{x θ n}^{(i)}, {\bar{M}}_{θ x n}^{(i)}) s i n (n θ), \\ ({p_{x}}^{(i)}, {p_{z}}^{(i)}) = \sum_{n} ({\tilde{p}}_{x n}^{(i)}, {\tilde{p}}_{z n}^{(i)}) c o s (n θ), \\ {p_{θ}}^{(i)} = \sum_{n} {\tilde{p}}_{θ n}^{(i)} s i n (n θ), (i = 1, \dots, 4), \end{array},

where the labeled “ $\bar{}$ ”variables stand for undermined dimensionless state variables, which only are functions of non-dimension coordinates, $δ = x / L$ . For convenience, the summation subscript n would be omitted in the back derivation.

Combining Eqs. (17)-(19) and eliminating the variables ${\bar{N}}_{x}^{(i)}$ , ${\bar{N}}_{θ}^{(i)}$ , ${\bar{N}}_{θ x}^{(i)}$ , ${\bar{M}}_{x}^{(i)}$ , ${\bar{M}}_{θ}^{(i)}$ , ${\bar{Q}}_{x}^{(i)}$ and ${\bar{Q}}_{θ}^{(i)}$ ( $i =$ 1,…,4), the first order differential state equation of the $i$ th layer can be yielded as:

20

\frac{d}{d ξ} \{\begin{array}{l} {\bar{u}}^{(i)} \\ {\bar{v}}^{(i)} \\ \bar{w} \\ \bar{β} \\ {\bar{N}}_{x}^{(i)} \\ {\bar{S}}_{x}^{(i)} \\ {\bar{V}}_{x}^{(i)} \\ {\bar{M}}_{x}^{(i)} \end{array}\} = [\begin{array}{l} 0 & {g_{12}}^{(i)} & {g_{13}}^{(i)} & 0 & {g_{15}}^{(i)} & 0 & 0 & 0 \\ {g_{21}}^{(i)} & 0 & 0 & {g_{24}}^{(i)} & 0 & {g_{26}}^{(i)} & 0 & 0 \\ 0 & 0 & 0 & {g_{34}}^{(i)} & 0 & 0 & 0 & 0 \\ 0 & {g_{42}}^{(i)} & {g_{43}}^{(i)} & 0 & 0 & 0 & 0 & {g_{48}}^{(i)} \\ {g_{51}}^{(i)} & 0 & 0 & {g_{54}}^{(i)} & 0 & {g_{56}}^{(i)} & 0 & 0 \\ 0 & {g_{62}}^{(i)} & {g_{63}}^{(i)} & 0 & {g_{65}}^{(i)} & 0 & 0 & {g_{68}}^{(i)} \\ 0 & {g_{72}}^{(i)} & {g_{73}}^{(i)} & 0 & {g_{75}}^{(i)} & 0 & 0 & {g_{78}}^{(i)} \\ {g_{81}}^{(i)} & 0 & 0 & {g_{84}}^{(i)} & 0 & {g_{86}}^{(i)} & {g_{87}}^{(i)} & 0 \end{array}] • \{\begin{array}{l} {\bar{u}}^{(i)} \\ {\bar{v}}^{(i)} \\ \bar{w} \\ \bar{β} \\ {\bar{N}}_{x}^{(i)} \\ {\bar{S}}_{x}^{(i)} \\ {\bar{V}}_{x}^{(i)} \\ {\bar{M}}_{x}^{(i)} \end{array}\}

- \frac{L}{K^{i}} \{\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ {\tilde{p}}_{x}^{(i)} \\ {\tilde{p}}_{θ}^{(i)} \\ {\tilde{p}}_{z}^{(i)} \\ 0 \end{array}\}, (i = 1, \dots, 4) .

The values of $g_{i j}^{(1)}$ and $g_{i j}^{(4)}$ ( $i =$ 1, 2,…, 8; $j =$ 1, 2,…, 8) can be seen in the Appendix.

2.3. Equilibrium equation in the radial direction for transition layer and damping layer

As previous assumptions, ignoring the tensile rigidity, flexural rigidity and in-plane inertia for transition layer and damping layer, their equilibrium equations in the radial direction (see Fig. 4) can be can be written as:

21

{\tilde{p}}_{z}^{(12)} - {\tilde{p}}_{z}^{(23)} + ρ_{2} h_{2} ω^{2} \tilde{w} = 0,

22

{\tilde{p}}_{z}^{(23)} - {\tilde{p}}_{z}^{(34)} + ρ_{3} h_{3} ω^{2} \tilde{w} = 0 .

Combining Eqs. (20) and (21), the following equation can be obtained as follows:

23

{\tilde{p}}_{z}^{(12)} - {\tilde{p}}_{z}^{(34)} + ρ_{2} h_{2} ω^{2} \tilde{w} + ρ_{3} h_{3} ω^{2} \tilde{w} = 0,

where ${\tilde{p}}_{z}^{(12)}$ is the radial interaction between base layer and transition layer, ${\tilde{p}}_{z}^{(23)}$ is the radial interaction between transition layer and damping layer, ${\tilde{p}}_{z}^{(34)}$ is the radial interaction between damping layer and constrained layer.

Fig. 4The radial interactions between layers

2.4. Force action on base layer and constrained layer

In the state vector Eq. (20), ${\tilde{p}}_{x}^{(i)}$ , ${\tilde{p}}_{θ}^{(i)}$ , ${\tilde{p}}_{z}^{(i)}$ ( $i =$ 1,.., 4) which is called acting forces include interactions forces between all layers and external excitation force. The expressions of shear forces for transition layer and damping layer have been given in Eqs. (15) and (16). Applying the Fourier expansions in circumferential direction to Eqs. (15) and (16) and introducing dimensionless variables, ${\tilde{τ}}_{z x}^{(2)}$ , ${\tilde{τ}}_{z θ}^{(2)}$ , ${\tilde{τ}}_{z x}^{(3)}$ and ${\tilde{τ}}_{z θ}^{(3)}$ (see Fig. 5) can be written as:

24

\{\begin{array}{l} {\tilde{τ}}_{z x}^{(2)} = {\tilde{τ}}_{z x}^{(3)} = G_{2} {\tilde{γ}}_{z x}^{(2)} = G_{3} {\tilde{γ}}_{z x}^{(3)} = T_{1} {\bar{u}}^{1} + T_{2} \bar{β} + T_{3} {\bar{u}}^{3}, \\ {\tilde{τ}}_{z θ}^{(2)} = {\tilde{τ}}_{z θ}^{(3)} = G_{2} {\tilde{γ}}_{z θ}^{(2)} = G_{3} {\tilde{γ}}_{z θ}^{(3)} = T_{4} {\bar{v}}^{1} + T_{5} \bar{w} + T_{6} {\bar{v}}^{3}, \end{array}

where:

T_{1} = - \frac{G_{2} G_{3}}{G_{2} h_{3} + G_{3} h_{2}} L, T_{2} = - \frac{G_{2} G_{3} (2 h_{2} + 2 h_{3} + h_{1} + h_{4})}{2 (G_{2} h_{3} + G_{3} h_{2})},

T_{3} = \frac{G_{2} G_{3}}{G_{2} h_{3} + G_{3} h_{2}} L, T_{4} = - \frac{G_{2} G_{3} e (2 R_{1} + h_{1})}{4 g} L,

T_{5} = (- L n G_{2} G_{3}) \frac{e h_{1} + f h_{4} + I}{4 g}, T_{6} = \frac{G_{2} G_{3} (2 R_{4} - h_{4}) f}{4 g} L .

Fig. 5Shear forces in transition layer and damping layer

a) Transition layer

b) Damping layer

Considering the interactions between layers and the external excitation mentioned above, the forces ${\tilde{p}}_{x}^{(1)}$ , ${\tilde{p}}_{θ}^{(1)}$ , ${\tilde{p}}_{z}^{(1)}$ , ${\tilde{p}}_{x}^{(4)}$ , ${\tilde{p}}_{θ}^{(4)}$ and ${\tilde{p}}_{z}^{(4)}$ can be obtained as follows:

25

\{\begin{array}{l} {\tilde{p}}_{x}^{(1)} = {\tilde{f}}_{x}^{(1)} + {\tilde{τ}}_{z x}^{(2)}, {\tilde{p}}_{θ}^{(1)} = {\tilde{f}}_{θ}^{(1)} + {\tilde{τ}}_{z θ}^{(2)}, \\ {\tilde{p}}_{z}^{(1)} = {\tilde{f}}_{z}^{(1)} - {\tilde{p}}_{z}^{(12)} + (\frac{e_{1}}{L}) \frac{d {\tilde{τ}}_{z x}^{(2)}}{d ξ} + n (\frac{e_{1}}{R_{1}}) {\tilde{τ}}_{z θ}^{(2)}, \end{array}

26

\{\begin{array}{l} {\tilde{p}}_{x}^{(4)} = {\tilde{f}}_{x}^{(4)} - {\tilde{τ}}_{z x}^{(3)}, {\tilde{p}}_{θ}^{(4)} = {\tilde{f}}_{θ}^{(4)} - {\tilde{τ}}_{z θ}^{(3)}, \\ {\tilde{p}}_{z}^{(4)} = {\tilde{f}}_{z}^{(4)} + {\tilde{p}}_{z}^{(34)} + (\frac{e_{4}}{L}) \frac{d {\tilde{τ}}_{z x}^{(3)}}{d ξ} + n (\frac{e_{4}}{R_{4}}) {\tilde{τ}}_{z θ}^{(3)} . \end{array}

In which, $e_{1} = (h_{1} + h_{2} + h_{3}) / 2$ , $e_{4} = (h_{2} + h_{3} + h_{4}) / 2$ . ${\tilde{f}}_{x}^{(1)}$ , ${\tilde{f}}_{θ}^{(1)}$ , ${\tilde{f}}_{z}^{(1)}$ and ${\tilde{f}}_{x}^{(4)}$ , ${\tilde{f}}_{θ}^{(4)}$ , ${\tilde{f}}_{z}^{(4)}$ are amplitudes of external excitation on base layer and constrained layer along $x$ , $θ$ , $z$ -directions, respectively. In case of free vibration, they are equal zero. It can be seen from Eqs. (25) and (26) that the effect of shear force eccentricity on the radial acting forces has been considered.

3. Integrated first-ordinary matrix differential equation of TTLDS

It is obvious that the differential Eq. (20) cannot be solved directly for the unknown radial interaction ${\tilde{p}}_{z}^{(12)}$ and ${\tilde{p}}_{z}^{(34)}$ in Eqs. (25) and (26). Therefore, it needs to eliminate them from Eq. (20). By substituting Eq. (25) and (26) into Eq. (20) respectively and using Eq. (23) eliminate the unknown radial interaction and numbers of non-independent variable, the integrated first order ordinary matrix differential equation of TTLDS can be expressed by:

27

\bar{B} \frac{d}{d ξ} Z = \bar{A} Z + \bar{F},

where $\bar{Z} = {\{{\bar{u}}^{(1)}, {\bar{v}}^{(1)}, w, \bar{β}, {\bar{N}}_{x}^{(1)}, {\bar{S}}_{x}^{(1)}, ({\bar{V}}_{x}^{(1)} + \frac{K^{(4)}}{K^{(1)}} {\bar{V}}_{x}^{(4)}), {\bar{M}}_{x}^{(1)}, {\bar{u}}^{(4)}, {\bar{v}}^{(4)}, {\bar{N}}_{x}^{(4)}, {\bar{S}}_{x}^{(4)}\}}^{T},$ is called the integration state vector of TTLDS; $\bar{A}$ and $\bar{B}$ are the coefficient matrices with the order 12×12 and has been listed in the Appendix. $\bar{F} = {\{0,0, 0,0, {\bar{\bar{p}}}_{x}^{(1)}, {\bar{\bar{p}}}_{θ}^{(1)}, {\bar{\bar{p}}}_{z}^{(1 + 4)}, 0,0, 0, {\bar{\bar{p}}}_{x}^{(4)}, {\bar{\bar{p}}}_{θ}^{(4)}\}}^{T}$ is the vector of non-dimension external excitation. The elements of $\bar{F}$ are the follows:

28

\{\begin{array}{l} {\bar{\bar{p}}}_{x}^{(1)} = - (\frac{L}{K^{(1)}}) {\tilde{f}}_{x}^{(1)}, {\bar{\bar{p}}}_{θ}^{(1)} = - (\frac{L}{K^{(1)}}) {\tilde{f}}_{θ}^{(1)}, \\ {\bar{\bar{p}}}_{x}^{(4)} = - (\frac{L}{K^{(4)}}) {\tilde{f}}_{x}^{(4)}, {\bar{\bar{p}}}_{θ}^{(4)} = - (\frac{L}{K^{(4)}}) {\tilde{f}}_{θ}^{(4)}, \\ {\bar{\bar{p}}}_{z}^{(1 + 4)} = - (\frac{L}{K^{(1)}}) ({\tilde{f}}_{z}^{(1)} + - {\tilde{f}}_{z}^{(4)}) . \end{array}

Since $|\bar{B}| > 1$ and ${[\bar{B}]}^{- 1}$ exists, the matrix differential Eq. (26) can be solved.

4. The semi-analytical solution to vibration and damping characteristics of TTLDS

Eq. (27) can be solved effectively by using homogeneous high precise integration method. When TTLDS is in free vibration, which means the external excitation $\bar{F}$ in Eq. (27) being zero, the relationship of the state vectors between $x =$ 0 and $x = L$ can be found:

29

S (L) = T \cdot S (0),

where $S (0)$ and $S (L)$ denote the integration state vectors at $x =$ 0 and $x = L$ respectively, $T$ is the transfer matrix.

Usually, there are six state variables undetermined and six boundary conditions given at $x =$ 0 and $x = L$ . Substituting the boundary conditions given into Eq. (29), the equation that to be solved can be expressed by:

30

\bar{T} \cdot \bar{S} (0) = O,

where $\bar{S} (0)$ are the six undetermined state variables at $x =$ 0. Since six undetermined state variables can’t be all zeros, the coefficient determinant is zero. The characteristic equation can be written by:

31

d e t (\bar{T}) = 0 .

By solving Eq. (31), the $i$ th mode complex eigenvalue $s_{i}$ of the TTLDS can be achieved.

The $i$ th mode natural frequency and loss factor of TTLDS can be written as:

32

f_{i} = \frac{R e (s_{i})}{2 π},

33

η_{i} = 2 I m (s_{i}) / \sqrt{{(R e (s_{i}))}^{2} + {(I m (s_{i}))}^{2}} .

5. Model validation

To illustrate the correctness of the paper method, the TTLDS that simply supported at two ends is considered. The geometric and physical parameters are: $R_{1} =$ 0.3 m, $L =$ 0.1 m, $h_{1} =$ 3 mm, $h_{2} =$ 0.5 mm, $h_{3} =$ 0.5 mm, $h_{4} =$ 2 mm, $E_{1} = E_{4} =$ 70 GPa, $ρ_{1} = ρ_{4} =$ 2700 kg/m³, $μ_{1} = μ_{4} =$ 0.3, $ρ_{2} =$ 1300 kg/m³, $ρ_{3} =$ 999 kg/m³, $G_{2} =$ 52.5(1+0.3862i) MPa, $G_{3} =$ 0.896(1+0.9683i) MPa.

Using the paper method and FEM solve the TTLDS, the results comparison between the proposed method and FEM are shown in Table 1.

It can be seen from Table 1 that the error of natural frequency and loss factor between paper method and FEM is less than 3 %. The result comparison shows that semi-analytical method is reliable and can be used analyze the damping characteristics of TTLDS.

Table 1The results comparison between paper method and FEM

Circumferential wave number ( $n$ )	Natural frequency Hz			Loss factor %
Circumferential wave number ( $n$ )	Paper method	FEM	Error (%)	Paper method	FEM	Error (%)
9	2306.94	2333.31	1.13	0.491	0.497	1.19
8	2294.1	2345.24	2.18	0.796	0.804	0.89
10	2302.1	2350.05	2.04	0.902	0.911	0.89
7	2344.07	2386.06	1.76	0.622	0.629	0.96
11	2352.14	2394.04	1.75	0.963	0.974	1.03
6	2420.28	2455.15	1.42	0.545	0.551	1.04

6. The parameters analysis for transition layer

6.1. The thickness parameter analysis

Taking a TTLDS which being clamped at both ends into account, its geometric and physical parameters are $L =$ 100 mm, $R_{1} =$ 143 mm, $h_{1} =$ 2 mm, $h_{3} =$ 0.5 mm, $h_{4} =$ 0.5 mm, $E_{1} =$ 212 GPa, $E_{4} =$ 70 GPa, $μ_{1} =$ 0.3, $μ_{4} =$ 0.3, $ρ_{1} =$ 7850 kg/m³, $ρ_{2} =$ 1350 kg/m³, $ρ_{3} =$ 999 kg/m³, $ρ_{4} =$ 2700 kg/m³, $G_{2} =$ 5.25(1+0.3862) MPa, $G_{3} =$ 0.896(1+0.9683i) MPa.

The thicknesses of transition layer $h_{2}$ are 0.2, 0.4, 0.6 and 0.8 mm respectively. The trends of natural frequency and damping factor are shown in Fig. 6.

From Fig. 6, it can be seen that with the thickness increasing, the natural frequency of structure shows a gradual downward trend and the loss factor shows a gradual upward trend. So, on the premise of meeting structure size and weight, the structural damping effect can be improved by increasing the thickness of transition layer. The changing trends of natural frequency and loss factor for structure under different thickness of transition layer are shown in Fig. 6.

6.2. The analysis of material properties

The shear modulus $G_{2}$ for four different materials are 8.582×10⁶(1+0.5478i), 5.72×10⁷(1+0.4258i), 2.9×10⁸(1+0.3478i) and 6.58×10⁹(1+0.1028i) respectively, and remaining parameters are the same as the mode in section 6.1. The trend of natural frequency and loss factor for structure are shown in Fig. 7.

Fig. 6The comparison of natural frequency and damping factor for transition layer with different thicknesses

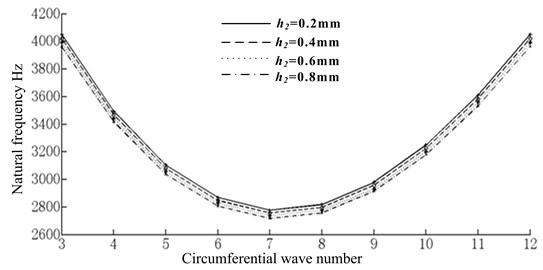
a) The comparison of natural frequency

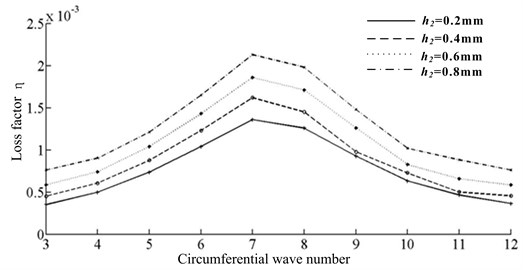
b) The comparison of loss factor

From Fig. 7, it can be seen that with hardness of material increasing for transition layer, the natural frequency of structure presents the first decreasing then increasing trend, and the loss factor of structure presents the first increasing then deceasing trend. The trends indicate that the structure damping effect can be changed by changing the material of transition layer. In general, the material property of transition layer is between the material of base layer and damping layer. When the elastic modulus ratio $E_{2} / E_{3}$ is 1000, the best damping effect can be achieved. The trends of natural frequency and loss factor for structure are shown in Fig. 7.

6.3. The analysis of transition layer’s location

As described in the beginning of the paper, in order to increase structural damping effect, we added one more layer which called transition layer between base layer and damping layer of TTDS to form TTLDS (B-T-D-C). Now supposed that transition layer is located between damping layer and constraining layer of TTDS, which plays a similar constrained role like the constrained layer on increasing the shear deformation and shear stress of damping layer on consuming more vibration energy, and formed another TTLDS (B-D-T-C) (see Fig. 1(b)), which effect is better?

Aimed at this problem, the paper takes two different materials as transition layer respectively and compares their effects. The shear modulus of two materials are $G_{2} =$ 8.582× 10⁶(1+0.5478i) and $G_{2} =$ 2.9×10⁸(1+0.3478i). Other parameters still are the same as the model above. The comparisons of natural frequency and loss factor for structure between B-T-D-C and B-D-T-C are shown in Table 2 and Table 3.

Fig. 7The comparison of natural frequency and damping factor for transition layer with different materials

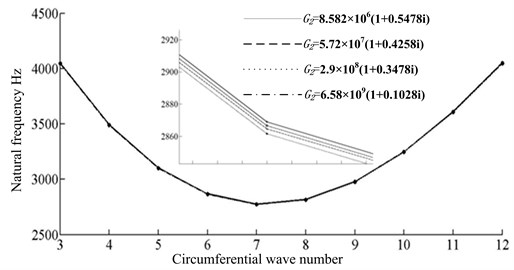
a) The comparison of natural frequency

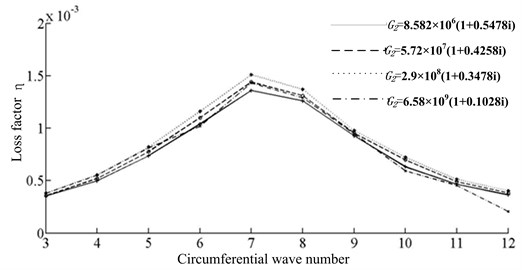
b) The comparison of loss factor

Table 2The comparison of natural frequency and loss factor for first material between two models

Circumferential wave number ( $n$ )	Natural frequency		Loss factor
Circumferential wave number ( $n$ )	B-D-T-C	B-T-D-C	B-D-T-C	B-T-D-C
3	4051.84	4045.53	3.521×10^-4	3.543×10^-4
4	3493.78	3490.44	4.980×10^-4	5.012×10^-4
5	3104.12	3098.74	7.362×10^-4	7.565×10^-4
6	2868.98	2861.58	1.042×10^-3	1.245×10^-3
7	2776.78	2698.33	1.362×10^-3	1.464×10^-3
8	2817.76	2809.23	1.261×10^-3	1.384×10^-3

Table 3The comparison of natural frequency and loss factor for second material between two models

Circumferential wave number ( $n$ )	Natural frequency		Loss factor
Circumferential wave number ( $n$ )	B-D-T-C	B-T-D-C	B-D-T-C	B-T-D-C
3	4040.83	4035.15	3.831×10^-4	3.934×10^-4
4	3484.35	3480.6	5.552×10^-4	5.654×10^-4
5	3095.82	3091.25	8.213×10^-4	8.435×10^-4
6	2861.58	2857.51	1.161×10^-3	1.193×10^-3
7	2769.58	2761.52	1.512×10^-3	1.615×10^-3
8	2810.58	2805.31	1.312×10^-3	1.394×10^-3

From Table 2 and Table 3, it can be seen that for the same material in different position, damping effect of B-T-D-C is better than that of B-D-T-C, which means the transition layer located between base layer and damping layer can increase shear deformation of the damping layer more than that of located between damping layer and constrained layer.

7. Conclusions

The paper presents a type tubular transition layer damping structure which added a transition layer between base layer and damping layer of TTDS. Based on the basic equation of TTLDS, considering the influence of energy dissipation for transition layer and damping layer and the interaction between layers, the integration of first order differential equation of TTLDS is derived firstly under external excitation. To obtain the characteristics of frequency and loss factor for TTLDS, the homogeneous high precise integration method is applied to solve the differential equations. Finally, the paper discusses the effects of parameters for transition layer on the structural damping and achieves the following conclusions:

1) The thickness of transition layer can play a significant role on structural damping effect. On the premise of meeting the structure size and weight, the structural damping effect can be improved by increasing the thickness of transition layer.

2) The material of transition layer can make a great influence on damping effect of the structure. In practice, the damping effect can be improved by changing the material of transition layer. When the elastic modulus ratio of the two materials $E_{2} / E_{3}$ is 1000, the damping effect will be the best.

3) The location of transition layer can play some role on damping effect. For the same material, the damping effect located in between base layer and damping layer is better than that of located in between damping layer and constrained layer.

References

Sainsbury M. G., Mastic R. S. Vibration damping of cylindrical shells using strain-energy-based distribution of an add-on viscoelastic treatment. Finite Elements in Analysis and Design, Vol. 43, Issue 3, 2007, p. 175-192.

Publisher
Xiang Y., Huang Y. Y., Lu J., Yuan L. T., Zhou S. Z. A new matrix method for analyzing vibration and damping effect of a sandwich circular cylindrical shell with a viscoelastic core. Applied Mathematics and Mechanics, Vol. 29, Issue 12, 2008, p. 1443-1456.

Publisher
Cao X. T., Zhang Z. Y., Hua H. X. Free vibration of circular cylindrical shell with constrained layer damping. Applied Mathematics and Mechanics, Vol. 32, Issue 4, 2011, p. 470-482.

Publisher
Liu C. F., Li Y. N., Zheng L., Fang Z. P. Topology optimization and tests for a short cylindrical shell with constrained layer damping. Journal of Vibration and Shock, Vol. 32, Issue 18, 2013, p. 49-59.

Search CrossRef
Shi H. R., Gao P., Li Z. G., Zhao D. Y., Zhang J. P. Vibration analysis and optimization of a cylindrical shell with constrained layer damping. Journal of Vibration and Shock, Vol. 32, Issue 22, 2013, p. 146-151.

Search CrossRef
Chen, T. H., Z. Z., Shen, Y. D. Analysis of cylindrical sandwich aluminum shell with viscoelastic damping treatment. Advances in Materials Science and Engineering, Vol. 1049, Issue 2013, 2013, p. 3-9.

Publisher
Chen M. X., Xie K., Wei J. H. Vibration characteristics of multiple cabins of cylindrical shell. Journal of Vibration Engineering, Vol. 27, Issue 4, 2014, p. 555-564.

Search CrossRef
Wang X. L., Sun L. L., Yang M. Y., Gao Y. Vibrational characteristics of a power machinery mounted in a circular cylindrical shell through inclined isolators. Journal of Vibration Engineering, Vol. 28, Issue 2, 2015, p. 227-236.

Search CrossRef
Yan B. J., Zhang W. J., Li Z. L., Sun D. G. Distributed parameter transfer function method for dynamic response of a constrained damping structure with transition layer. Journal of Vibration and Shock, Vol. 35, Issue 5, 2016, p. 186-190.

Search CrossRef
Yellin J. M., Shen I. Y., Reinhall P. G. An analytical and experimental analysis for a one-dimensional passive stand-off layer damping treatment. Journal of Vibration and Acoustics, Vol. 122, Issue 4, 2000, p. 440-447.

Publisher
Wei Z. Y., Shi X. H., Li S. C., Jiao L. F. Modeling and simulation of a constrained damping beam with slotted stand-off layer. Mechanical Science and Technology for Aerospace Engineering, Vol. 28, Issue 7, 2009, p. 876-880.

Search CrossRef
Shi H. R., Zhao D. Y. Reducing vibration and optimization design of beam with a stand-off constrained layer damping patch. Journal of Machine Design, Vol. 12, Issue 27, 2010, p. 79-83.

Search CrossRef
Vuure A. W. V., Verpoest I., Ko F. K. Sandwich-fabric panels as spacers in a constrained layer structural damping application. Composites Part B: Engineering, Vol. 32, Issue 1, 2001, p. 11-19.

Publisher
Kumar S., Kumar R., Sehgal R. Enhance ACLD treatment using stand-off layer: FEM based design and experimental vibration analysis. Applied Acoustics, Vol. 72, Issue 11, 2011, p. 856-872.

Publisher
Zhao C. Y., Wang P. Theoretical modeling and effectiveness study of slotted stand-off layer damping treatment for rail vibration and noise control. Shock and Vibration, Vol. 2015, 2015, p. 1-12.

Publisher
Mastic R. S., Sainsbury M. G. Vibration damping of cylindrical shells partially coated with a constrained viscoelastic treatment having a standoff layer. Thin-Walled Structure, Vol. 43, Issue 9, 2005, p. 1355-1379.

Publisher
Xiang Y., Huang Y. Y., Huang J. Q. A method of homogenization of high precision direct integration. Huazhong University of Science and Technology, Nature Science Edition, Vol. 30, Issue 11, 2002, p. 74-76.

Search CrossRef
Wang H. J., Chen L. W. Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer. Finite Elements in Analysis and Design, Vol. 40, Issue 7, 2004, p. 737-755.

Publisher
Li E. Q., Li D. K., Tang G. J., Lei Y. J. Dynamic analysis of cylindrical shell with partially covered ring-shape constrained layer damping by transfer function method. Acta Aeronautica Et Astronautica Sinica, Vol. 28, Issue 6, 2007, p. 1487-1493.

Search CrossRef
Wang M., Fang Z. C. Coupled vibration control of cylindrical shells partially treated with an active constrained layer damping. Chinese Journal of Applied Mechanics., Vol. 22, Issue 4, 2005, p. 545-550.

Search CrossRef
Xü Z. L. Elastic Mechanics (Part II). People’s Education Press, BeiJing, 1982.

Search CrossRef
Chen L. H., Huang S. C. Vibrations of a cylindrical shell with partially constrained layer damping (CLD) treatment. International Journal of Mechanical Sciences, Vol. 41, Issue 12, 1999, p. 1485-1498.

Publisher

Cited by

Torsional Vibration Response Characteristics and Structural Optimization of Compressor Shaft System Considering the Effect of Variable Inertia

Zhiqiang Huang | Tao Li | Zhen Chen | Kehai Zhang | Zhiyong Wang

(2022)

About this article

Received

12 January 2017

Accepted

17 July 2017

Published

15 February 2018

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2017.18172

Keywords

tubular structure

transition layer

natural frequency

loss factor

damping effect

Acknowledgements

This project is supported by National Natural Science Foundation of China (Grant No. 51405323) and Startup Foundation for Doctors of Taiyuan University of Science and Technology (Grant No. 20162005, 20162035).

Author Contributions

Wenjun Zhang performed the data analyses and wrote the manuscript. Dagang Sun contributed to the conception of the study. Bijuan Yan contributed to the conception of the study. Zhanlong Li contributed to the paper revision. Shizhong Liu helped perform the analysis with constructive discussions.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 03 31

Effects of foundation mass on dynamic responses of beams subjected to moving oscillators

T. Phuoc Nguyen, D. Trung Pham, P. Hoa Hoang

Research article

2019 04 25

Dynamic response of structures with tuned mass dampers in modal coordinates

Jan Štěpánek, Jiří Máca

Research article

2018 03 31

An analytical model for determining the effect of damping on 3D natural frequency of reinforced walls

Alireza Darvishpour, Ali Ghanbari, S. A. A. Hosseini, Masoud Nekooei, Tayyebeh Darvishpour

Research article

2016 11 15

Dynamic response prediction of non-obstructive particle damping using principles of gas-solid flows

Xiaofei Lei, Chengjun Wu

W. Zhang, D. Sun, B. Yan, Z. Li, and S. Liu, “The semi-analytical method for damping of tubular transition layer damping structure,” Journal of Vibroengineering, Vol. 20, No. 1, pp. 24–41, Feb. 2018, https://doi.org/10.21595/jve.2017.18172

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18172
UR  - https://doi.org/10.21595/jve.2017.18172
TI  - The semi-analytical method for damping of tubular transition layer damping structure
T2  - Journal of Vibroengineering
AU  - Sun, Dagang
AU  - Zhang, Wenjun
AU  - Yan, Bijuan
AU  - Li, Zhanlong
AU  - Liu, Shizhong
PY  - 2018
DA  - 2018/02/15
PB  - JVE International Ltd.
SP  - 24-41
IS  - 1
VL  - 20
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Sun_2018,
	doi = {10.21595/jve.2017.18172},
	url = {https://doi.org/10.21595/jve.2017.18172},
	year = 2018,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	number = {1},
	pages = {24--41},
	author = {Dagang Sun and Wenjun Zhang and Bijuan Yan and Zhanlong Li and Shizhong Liu},
	title = {The semi-analytical method for damping of tubular transition layer damping structure},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]D. Sun, W. Zhang, B. Yan, Z. Li, and S. Liu, “The semi-analytical method for damping of tubular transition layer damping structure,” Journal of Vibroengineering, vol. 20, no. 1, pp. 24–41, Feb. 2018, doi: 10.21595/jve.2017.18172.

Copy IEEE

Copied to clipboard!

Sun, Dagang, Wenjun Zhang, Bijuan Yan, Zhanlong Li, and Shizhong Liu. “The Semi-Analytical Method for Damping of Tubular Transition Layer Damping Structure.” Journal of Vibroengineering 20, no. 1 (February 15, 2018): 24–41. https://doi.org/10.21595/jve.2017.18172.

Copy Chicago

Copied to clipboard!

The semi-analytical method for damping of tubular transition layer damping structure

Abstract

1. Introduction

2. The governing equation of TTLDS

2.1. Shear deformation and shear force in transition layer and damping layer

2.2. Matrix differential equation of first order of state vector for base layer and constrained layer

2.3. Equilibrium equation in the radial direction for transition layer and damping layer

2.4. Force action on base layer and constrained layer

3. Integrated first-ordinary matrix differential equation of TTLDS

4. The semi-analytical solution to vibration and damping characteristics of TTLDS

5. Model validation

6. The parameters analysis for transition layer

6.1. The thickness parameter analysis

6.2. The analysis of material properties

6.3. The analysis of transition layer’s location

7. Conclusions

References

Cited by

About this article

Related Articles