Effects of isolator properties on viscous damper capacity of base isolated adjacent buildings

1. Introduction

Base isolation is a well-known and used technique which uncouples building from the disastrous effects of horizontal ground motions. Large horizontal flexibility and high vertical stiffness with recentering capability are the major characteristics of the isolator bearings placed generally base of building-type structures. The first feature mentioned decreases the risk of structural deformation by concentrating the maximum displacements at the isolator level while latter supports total superstructure weight above isolator bearings. Large base displacement stemmed from relative large displacement demand at the isolation level, requires a seismic gap (clearance) around building, especially during near-field ground motions. The interstorey drifts at the superstructure, however, decreases since the superstructure of the building supported by isolator bearings displaces as a rigid body for low- and mid-rise buildings on a rigid foundation. Thus, base isolators reduce the force demand on building by elongating the fundamental period.

In recent decades, pounding case of base isolated structures takes considerable attention by researchers. Agarwal et al. used Teflon bearings as base isolators under two degree-of-freedom modeled building. They investigated effects of the varying sliding friction coefficient on pounding numbers and impact forces [1]. Pant and Wijeyewickrema have studies on seismic pounding of a typical 4-storey base-isolated building with retaining walls at the base using 3D finite element analyses [2, 3]. Komodromos et al. and Komodromos investigated, through parametric studies, the effects of poundings of a base isolated building with the surrounding moat wall, revealing the potentially detrimental effects of structural impact on the effectiveness of seismic isolation [4, 5]. Mavronicola et al. studied on changes of peak responses of base isolated buildings pounding with varying impact models [6]. Masroor and Mosqueda have experimental and theoretical studies on the behavior of base isolated buildings impacting with different types of moat walls [7, 8]. Mitigation of seismic responses of base isolated structures during pounding is also studied. Shrimali et al. and Dumne et al. have researches on seismic response behavior of coupled buildings with base isolation and MR damper between adjacent floor levels [9, 10]. Base isolated rectangular liquid-storage tank is investigated by Cheng et al. to identify the pounding behavior due to near-field pulse-like earthquakes [11]. Gap dampers are also proposed to reduce displacement responses of base-isolated structures [12, 13].

In this paper, two adjacent base isolated buildings are investigated through severe ground motion in terms of impact forces under altering building storeys and dynamic characteristics of high-damping rubber bearing. The North-South acceleration record measured at Bolu station of 1999 Duzce earthquake (PGA 739.5 gal) is used as ground motion. The data includes near-field impulse-type motion which exhibits a strong pulse fling [14]. The buildings are likely to collide one another at floor levels during strong ground motions. Change in isolator characteristics leads to variation of displacement responses and thus impact forces during seismic motion because the isolator devices are able to shift the period of buildings. Therefore, pounding is inevitable for base isolated adjacent buildings which have different isolator characteristics. Viscous damper linkage between buildings may provide a solution for seismic response mitigation and pounding prevention. To the knowledge of author, even though there are structural pounding related studies, investigation of optimum damper capacity for base isolated adjacent buildings has never been presented before. Optimization procedure for linear viscous damper (LVD) capacities is applied for the cases including dampers installed at each adjacent floors and only top floor. The command of fmincon in Matlab Optimization Toolbox is used for optimization of viscous damper capacity. Seismic responses and LVD capacities are compared with the results of fixed base buildings.

2. Base isolation systems

Base isolation technology decouples the building from the ground and its harmful motions. Large horizontal flexibility allows the superstructure to have large displacement at the isolator level while the superstructure displaces as a rigid body minimizing interstorey drifts. Protection principle of isolation bearings is based on shifting the fundamental period of building and consequently reducing the seismic responses. There are different types of isolators produced based on same principle. This paper uses high-damping rubber bearing (HDRB) known as commonly used elastomeric bearings. It is basically composed of steel layers built in rubber. For dynamic analysis of isolated buildings, linear analyses may be conducted if the isolation system can be modeled with linear visco-elastic behavior. This is the case of devices such as laminated elastomeric bearings [15]. The restoring force produced by base isolator, $F_b$, which is parallel action of linear spring and damping is given by:

where $c_b$ and $k_b$ are damping coefficient and horizontal stiffness of isolation device, respectively. $x_b$ and ${\dot{x}}_b$ are displacement and velocity responses of base. Horizontal stiffness is assigned according to predetermined characteristics such as period ($T_b$) and damping ratio (${\xi }_b$) of base isolator:

in which $M_T$ denotes the total mass of the superstructure above the isolators and angular frequency of isolator, ${\omega }_b$, is given by $2\pi /T_b$. In this study, the period, $T_b$, is a variable between 1 and 3 sec while the damping ratio, ${\xi }_b$, is 10 %. Also, the base mass is assigned as 1.5 times the floor mass.

3. Governing equation of motions

The pounding force modeled by nonlinear elastic spring, i.e. the Hertz model, has been used for simplicity since the core of the study focuses on a parametric study presenting the effect of base isolator period on structural dynamic behavior. This model neglects the plastic deformations during pounding and assumes that nonlinear elastic spring become active when the gap ($a$) between buildings is closed. The equation of motion is written as in Eq. (4) including the impact force term, $F_p$. Force between two masses, $F_p$, is produced when relative displacement, $\delta \left(t\right)$, is larger than zero as given in Eq. (5):

where $\mathbf{M}$, $\mathbf{K}$ and $\mathbf{C}$ are mass, stiffness and damping matrices of coupled buildings while $\ddot{\mathbf{X}}$, $\dot{\mathbf{X}}$ and $\mathbf{X}$ is acceleration, velocity and displacement response matrices. $\mathbf{C}$ is determined by Rayleigh damping for each building. $r$ is influence coefficient matrix on the form of unit vector since only translational degree of freedom in the direction of earthquake are taken into account. ${\ddot{x}}_g$ is ground acceleration. Relative displacement is computed as $\delta \left(t\right)=x_1\left(t\right)-x_2\left(t\right)-a$, in which, $x_1\left(t\right)$ and $x_2\left(t\right)$ are the displacement responses of building 1 and 2 at time $t$. $R$ indicates constant stiffness coefficient of the nonlinear elastic spring. It takes between 40 kN/mm^3/2 and 80 kN/mm^3/2 (1.2×10⁹–2.6×10⁹ N/m^3/2) according to experimental analyses on concrete surfaces done by Van Mier et al. [16].

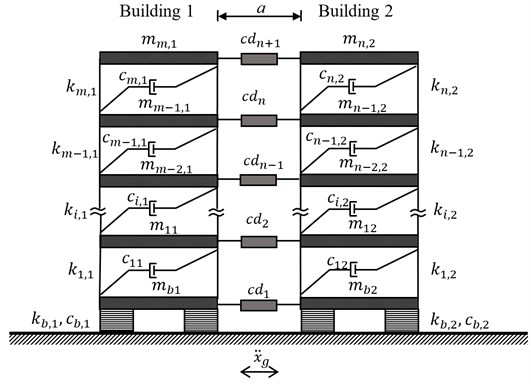
Fig. 1 shows coupled isolated buildings (building 1 and 2) connected by viscous dampers at each floor level. The mass, stiffness and damping coefficients of buildings are denoted as $m$, $k$ and $c$ while $cd$ is damping capacity of viscous damper. Subscript $b$ indicates base isolator. The seismic gap, $a$, which is determined based on storey height and number is assigned by provision given in Turkish Earthquake Code 2007 [17]. In this study, to focus on the effect of change in base isolator characteristics on the viscous damper capacity, the buildings are assumed to have same storey number ($m=n$). Also, the floors of buildings are in alignment so that the damper can be placed horizontally between adjacent floors.

Fig. 1A schematic of base-isolated adjacent buildings

For coupled base isolated multi-storey buildings with viscous dampers, the equation of motion is arranged as:

Mass matrices for building 1 and 2 with base isolators are given by ${\mathbf{M}}^1=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[m_{b1},m_{11},m_{21},\dots ,m_{m,1}]$ and ${\mathbf{M}}^2=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}[m_{b2},m_{12},m_{22},\dots ,m_{n,2}]$ in coupled mass matrix. Stiffness matrices, ${\mathbf{K}}^1$ and ${\mathbf{K}}^2$ and damping matrices, ${\mathbf{C}}^1$ and ${\mathbf{C}}^2$ also include base isolator stiffness and damping parameters, respectively. Displacement response vector is denoted as $\mathbf{X}={\{x_{b1},x_{11},x_{21},\dots ,x_{m,1},x_{b2},x_{12},x_{22},\dots ,x_{n,2}\}}^T$ whereas $\ddot{\mathbf{X}}$ and $\dot{\mathbf{X}}$ are acceleration and velocity response vectors. In supplemental viscous damper matrix, $\mathbf{C}\mathbf{d}\text{,}$$\left[\mathbf{A}\right]=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(cd\right)$ and $\left[-\mathbf{A}\right]=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(-cd\right)$ in which $cd$ is damper coefficient vector, i.e. $cd=\{{cd}_1,{cd}_2,\dots {,cd}_{n+1}\}$.

The computational models of the buildings are formed based on linear multi degree-of-freedom system which can be implemented by lumped mass-stiffness technique to represent shear-type structure. These models allow carrying out various cases for seismic response of structures equipped with base isolation devices with different characteristics and viscous dampers, used to control seismic behavior, with different capacities and locations. This study can optimize the positions and features of dampers.

4. Results

Some assumptions for computational model and analyses are necessary to present parametric study results in a convenient way and to highlight the efficiency of viscous damper usage for base isolated buildings. Two seismic isolated buildings which are the subject of this study are considered as symmetric in plan and the ground motion is assumed to be subjected in one direction at the base so that two-dimensional configuration is adequate to conduct seismic response analyses. The buildings are modeled as shear-type structure. The floors are in alignment and equal in height. The impact forces occur only on the floor levels and plastic deformations during pounding are neglected. The mass, stiffness and inherent damping coefficient are equally distributed among floors. The mass and stiffness for each storey are assigned as $m_{i,1}=m_{i,2}=$ 1×10⁵ kg and $k_{i,1}=$ 6.8×10⁷ N/m for building 1 and $k_{i,2}=$ 10×10⁸ N/m for building 2, respectively. The aim in the use of base isolation is to provide the superstructure above isolators behave in elastic range, thus the damping coefficient of buildings is considered as 2 %. The story numbers for both buildings are selected as 1, 5, 10 and 15 storey since base isolation system using elastomeric bearings is generally efficient for mid-rise buildings up to 15 storeys. Soil-structure interaction is neglected. The time response analyses under seismic motions are computed by Newmark-$\beta$ method.

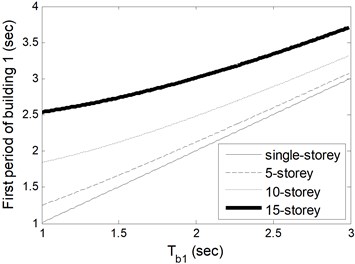
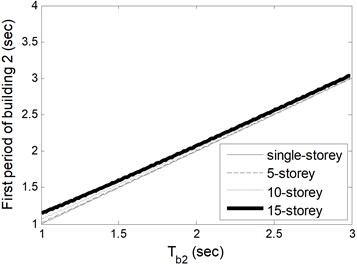
The fundamental period change of isolated buildings based on varied isolator periods is shown in Fig. 2. $T_{b1}$ and $T_{b2}$ denote the periods of isolators under building 1 and 2, respectively. As the storey number of building 1 increases, the fundamental period of building and isolator period began to diverge significantly from each other. However, the fundamental period of stiffer one (building 2) remains constant to the isolator’s. For single-storey buildings, the fundamental period of the building is elongated to that of isolator bearing. In other words, the flexibility of a building itself has no effect on fundamental dynamic characteristics.

Fig. 2Fundamental period change of a) building 1 based on Tb1 and b) building 2 based on Tb2

a)

b)

4.1. Variation of seismic responses and impact force based on isolator period

The analyses conducted in this section is to observe the seismic response and impact force changes under the circumstances of varied isolator periods while keeping the period of isolator under the other building fixed to 2 sec. The seismic gap is assigned as 3, 6, 11 and 16 cm according to TEC 2007 [17] for single, 5-, 10-, 15-storey buildings, respectively.

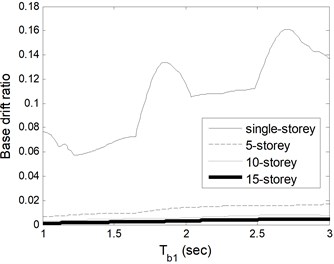
Fig. 3 illustrates maximum base displacements normalized by total height of building based on change of $T_{b1}$ and $T_{b2}$. Fig. 4(a) and (b) are slightly different from each other in respect of same storey number as expected because base displacement does not reflect involvement of the building stiffness. The single-storey building displaces largest among others since the rigidity of base isolator increases with increasing total mass of buildings, in other words the storey number. Furthermore, the roof displacement is a satisfactory indicator to show the involvement of building flexibility. Fig. 4(a) depicts the relative roof drift ratio (roof displacement relative to base normalized by total height of building) of building 1 for varied isolator period. If the figure is interpreted together with Fig. 2, it is clear that flexibility of building is very effective on seismic responses. On the contrary, the flexibility of building 2 is not effective on seismic responses at all as seen in Fig. 4(b).

Fig. 3Base drift ratio of a) building 1 based on Tb1 and b) building 2 based on Tb2

a)

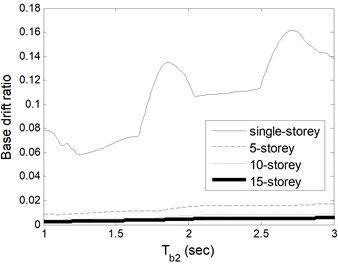
b)

Fig. 4Relative roof drift ratio of a) building 1 based on Tb1 and b) building 2 based on Tb2

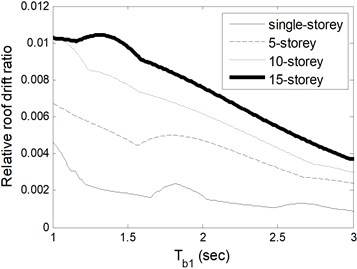
a)

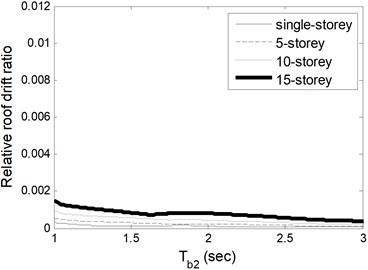
b)

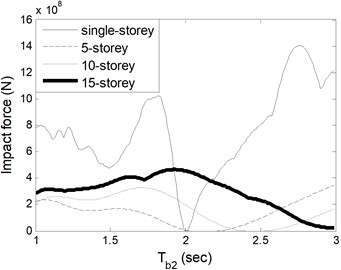
Fig. 5Impact forces of a) building 1 for varied Tb1 and b) building 2 for varied Tb2

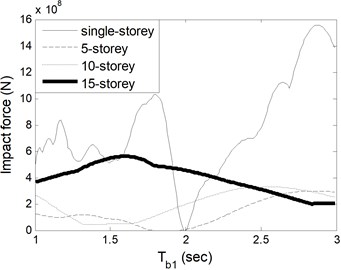
a)

b)

Table 1Minimum impact forces occurred on top floors of fixed base and isolated buildings

Storey No. of buildings 1/2	Minimum impact force (×108 N)
	Fixed base buildings [18]	Isolated buildings ($T_{b1}$)	Isolated buildings ($T_{b2}$)
01/01	0	0 (2 sec)	0 (2 sec)
05/05	1.14	0 (between 1.79 and 1.96 sec)	0 (between 2.04 and 2.21 sec)
10/10	2.05	0.40 (1.33 sec)	0 (between 2.40 and 2.52 sec)
15/15	3.70	2.05 (3 sec)	0.24 (3 sec)

In addition to seismic displacement responses of each building, impact forces of adjacent top floors are investigated based on varied isolator periods. In the analyses, the period of one isolator is changed between 1 sec and 3 sec, while the other is constant to 2 sec. For low-rise buildings, such as single- and 5-storey buildings, impact force can be vanished when $T_{b1}$ is 2 sec and lower. As the number of stories increases, pounding begins to occurs at all times. On the other hand, as $T_{b2}$ is changed, the impact force does not occur when using isolators with a period of 2 sec or longer. However, this is not valid for 15-storey building.

In Table 1, the impact forces are compared with the results of fixed base buildings [18] which have same structural characteristics such as mass and stiffness. It is clear that base isolated buildings takes lower, even zero, impact force values than fixed based buildings for specific values of periods of isolators.

4.2. Variation of linear viscous damper capacity based on isolator period

Damper coefficients needed to vanish the collision force between buildings will be determined under this subsection. Two damper placement cases are carried out in terms of optimum damper capacities; installation to each adjacent floor and only at the top floor.

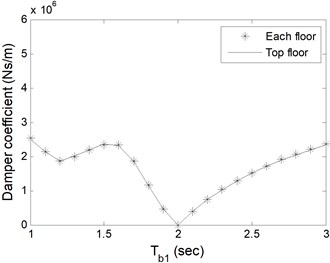
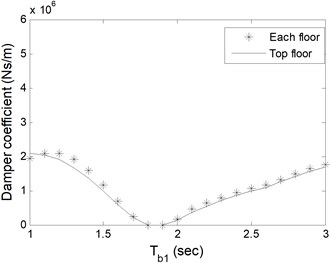
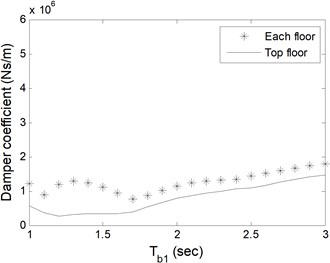
Fig. 6Total damper coefficients based on Tb1 of a) single-storey, b) 5-storey, c) 10-storey, d) 15-storey buildings

a)

b)

c)

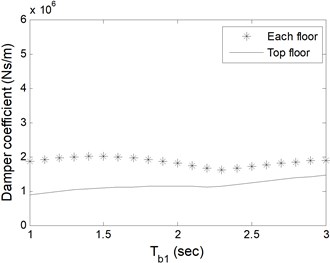
d)

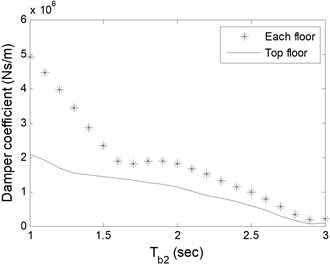
Fig. 7Total damper coefficients based on Tb2 of a) single-storey, b) 5-storey, c) 10-storey, d) 15-storey buildings

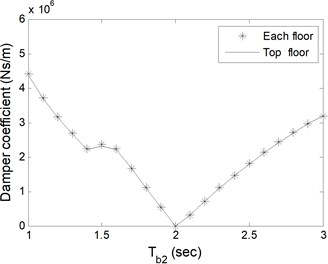
a)

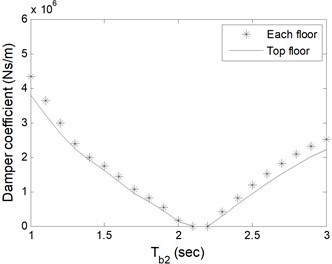
b)

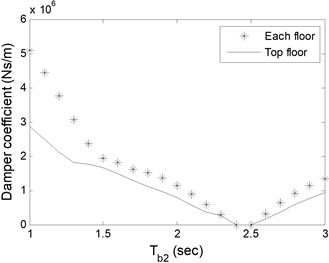
c)

d)

As expected, the damper coefficients are zero for the periods where zero impact forces occur as given in Table 1. In Fig. 6 and 7, for single- and 5-storey buildings, the trend in change of damper coefficients is similar to Fig. 5. For 10- and 15-storey buildings, the damper capacity remains almost constant as $T_{b1}$ alters in Fig. 6. Additional analyses which are not presented here show that single-storey coupled isolated buildings do not collide to each other as long as the periods of isolators under buildings are same. It is clear from figures that single damper installed at the top floor is adequate to prevent pounding with less total damper coefficient. Installation to each adjacent floor requires larger damper coefficient in total, however, smaller single damper. The decision about the damper capacity and number should be given by the designer and the manufacturer together in the aspect of economic and functional conditions.

Table 2 shows minimum damper capacities in total, irrespective of where the dampers are installed at. The results are consistent with and directly proportional to the impact forces in Table 1. Fixed base buildings require larger damper capacities for prevention of pounding.

Table 2Total damper coefficients installed

Storey No. of buildings 1/2	Minimum total damper coefficient (×105 Ns/m)
	Fixed base buildings [18]	Isolated buildings ($T_{b1}$)	Isolated buildings ($T_{b2}$)
01/01	0	0 (2 sec)	0 (2 sec)
05/05	1.715	0 (1.8 and 1.9 sec)	0 (2.1 and 2.2 sec)
10/10	23.92	2.58 (1.2 sec)	0 (2.4 and 2.5 sec)
15/15	45.00	8.95 (1 sec)	0.72 (2.9 sec)

5. Conclusions

The impact force responses and linear viscous damper capacity in terms of base isolator period are introduced in this paper. Seismic behavior of isolated buildings is highly affected by the period change in isolator bearings. Therefore, seismic response and impact force changes related to characteristics of bearings are summarized as follow:

1) For a predetermined period of base isolator, as the total weight of building increases, the horizontal stiffness of the isolator increase. Thus, the displacement responses get larger for the buildings with lower weight.

2) The seismic responses tend to increase at the base level as the isolator period increases. Especially for low-rise buildings, this situation is more observable.

3) For base isolated multi-storey buildings, flexibility of building affects the seismic response. Flexible buildings cause larger roof displacement relative to base.

4) Fixed base buildings results in larger impact forces than base isolated buildings.

Linear viscous dampers are proposed to connect adjacent buildings in order to prevent pounding. Optimum total damper capacities are computed by an optimization method for the cases when dampers are attached to each adjacent floor and only top floor. For low-rise buildings, both damper placement scenarios give almost same damper capacity to vanish impact forces. For mid-rise buildings, however, the damper capacity when attached only to the top floor is lower than the other case. Nevertheless, base isolated buildings require less damper capacity than fixed base buildings since lower impact forces occur.

In addition to demonstration of the comparative results of pounding structures with fixed base and base isolated, this study provides considerable outputs about seismic responses and LVD capacities for parametric analyses. Optimization of damper capacities for base isolated buildings is presented in this study as a first.