Attribute recognition model and its application of risk assessment for slope stability at tunnel portal

Zhang, Qian; Wang, Jing-chun; Zhang, Hai-xia

doi:10.21595/jve.2017.17869

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2017

Check for updates

Attribute recognition model and its application of risk assessment for slope stability at tunnel portal

Qian Zhang¹

Jing-chun Wang²

Hai-xia Zhang³

¹Structure Health Monitoring and Control Institute, Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

²Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

³Beijing General Municipal Engineering Design and Research Institute Co. Ltd., 100082 Beijing, China

Corresponding Author:

Jing-chun Wang

Cite the article Download PDF

Downloads 1430

WoS Core Citations 12

CrossRef Citations 11

Abstract

Due to large span and complex construction technology, the portal section of tunnel is vulnerable to the threats of latent slope failures such as landslide, spalling and collapse. In the present paper, to ensure the construction safety of tunnel, the attribute recognition model of risk assessment for the slope stability at tunnel portal was established by using attribute mathematics theory. The integrated degree of rock mass, lithological feature, geological structural feature, weathering degree, seismic intensity, gradient, rainfall and construction factors were selected as the indices of the risk assessment for the stability slope at tunnel portal with grading criteria of each index. Moreover, the weights of the assessment indices were determined by the judgment matrix constructed from analytic hierarchy process. The attribute measurement functions were used to compute attribute measurement of single index and synthetic attribute measurement. The identification and classification of risk assessment for the slope stability at tunnel portal were assessed using the confidence criterion. For practical purposes, the stability of slope located in portal of an actual Tunnel, i.e., Jiefangcun Tunnel in Cheng-Lan Railway, was evaluated based on the previously established attribute recognition model. The corresponding risk treatment measures were then proposed based on the assessment results and monitor results to ensure the construction safety of tunnel portal.

1. Introduction

Due to large span and complex construction technology, the portal section of tunnel is vulnerable to the threats of latent slope failures such as landslide, spalling and collapse. In addition, the surrounding rock of tunnel portal has shallow burial depth, poor stability and complex geological structural conditions. Some studies conducted with the behavior of slope stability at tunnel portal were due to Barisone [1], Giani [2], Quek and [3] Lee [4] and Peila [5]. These studies were very helpful in understanding the behavior of slope stability at tunnel portal. As to the analysis of the risk assessment on engineering, “Guidelines for Tunnel Risk Management” was proposed by the International Tunneling Association [6]. Many studies were subsequently carried out to analyze the risk of seismic damage of tunnel portal, stability of slope and water inrush by using fuzzy analytical method and extension assessment method [7-16].

However, few studies are concerned on the most direct factor related to slope safety, and very limited data are available for the assessment systems reflecting the change of slope condition. Due to the random determination of membership function to a certain extent, the conditions of unclear classification and unreasonable results may be analyzed by using fuzzy analytical method [17]. Based on the concepts of attribute set, attribute measure space and ordered partition class, Cheng [18] proposed the attribute recognition model to solve the comprehensive assessment. Recently, the attribute mathematics theory was applied successfully in the field of rock engineering. However, few relevant studies on slope stability at tunnel portal derived from attribute mathematics theory were conducted. Therefore, to evaluate the slope stability at tunnel portal, there is a need to establish the attribute recognition model of risk assessment for the slope stability at tunnel portal by using attribute mathematics theory.

In the present paper, the integrated degree of rock mass, lithological feature, geological structural feature, weathering degree, seismic intensity, gradient, rainfall and construction factors were selected as the indices of the risk assessment for stability slope at tunnel portal with grading criteria of each index. Moreover, the weights of the assessment indices were determined by using the judgment matrix. The attribute measurement functions were used to compute the attribute measurement of single index and synthetic attribute measurement. The identification and classification of risk assessment for the slope stability at tunnel portal were assessed by using the confidence criterion. For practical purposes, the stability of slope located in portal of an actual Tunnel, i.e., Jiefangcun Tunnel in Cheng-Lan Railway, was evaluated based on the previously established attribute recognition model. Based on the assessment results and monitor results, the corresponding risk treatment measures were then proposed to ensure the construction safety of tunnel portal.

2. Attribute recognition model of risk assessment for slope stability at tunnel portal

In practice, attribute mathematics theory is commonly used to analyze the risk of slope stability at tunnel portal. Following the suggestion of Cheng [18], the attribute comprehensive assessment system can be divided into three subsystems: attribute measure system of single index, comprehensive attribute measure system of multiple indices and attribute recognition analysis.

The risk assessment for slope stability at tunnel portal is a comprehensive assessment system with discrimination for slope instability by using the influencing factors. $X$ is assumed to be the evaluated object space, and the evaluated object $x_{i}$ ( $i =$ 1, 2,…, $n$ ) has $m$ evaluated indices $I_{j}$ ( $j =$ 1, 2,…, $m$ ). The value of the $j$ -th evaluated index $I_{j}$ in $x_{i}$ , $t_{j}$ , is divided into $K$ kinds of assessment grades $C_{k}$ ( $k =$ 1, 2,…, $K$ ). The attribute space $F$ adopted as {grades of slope stability at tunnel portal} is assumed to equal to $\{C_{1}, C_{2}, \dots, C_{K}\}$ , where each kind of circumstance is the attribute set.

The corresponding attribute measures of different attribute sets satisfying additivity rule can be obtained from the attribute arithmetic. The single-index attribute measure $μ_{x j k}$ shows that the measured value of the $j$ -th evaluated index $I_{j}$ of evaluated object, $t_{j}$ , can be computed with the size of attribute $C_{k}$ , whereas the comprehensive attribute measure $μ_{x k}$ shows that the evaluated object can be calculated using the size of grade $C_{k}$ [18].

2.1. Analysis of single-index attribute measure

Based on the determination method of attribute measure $μ_{x j k} = μ$ ( $x_{i j} \in C_{k}$ ) ( $1 \leq k \leq K$ ), the attribute measure functions (see Table 1) can be established.

Table 1Grade subdivision of single index

Indices	Assessment grades
Indices	$C_{1}$	$C_{2}$	…	$C_{K}$
$I_{1}$	$a_{10}$ - $a_{11}$	$a_{11}$ - $a_{12}$	…	$a_{1 K - 1}$ - $a_{1 K}$ or >(<) $a_{1 K}$
$I_{2}$	$a_{20}$ - $a_{21}$	$a_{21}$ - $a_{22}$	…	$a_{2 K - 1}$ - $a_{2 K}$ or >(<) $a_{2 K}$
…			…
$I_{m}$	$a_{m 0}$ - $a_{m 1}$	$a_{m 1}$ - $a_{m 2}$	…	$a_{m K - 1}$ - $a_{m K}$ or >(<) $a_{m K}$

In Table 1, $a_{j k}$ ( $k =$ 0, 1,…, $K$ ) is the upper or limiting value in the range interval of assessment gradessatisfying $a_{j 0} < a_{j 1} < \dots < a_{j K}$ or $a_{j 0} > a_{j 1} > \dots > a_{j K}$ . One obtains:

1

b_{j k} = \frac{a_{j k - 1} + a_{j k}}{2},

2

d_{j k} = m i n \{|b_{j k} - a_{j k}|, |b_{j k + 1} - a_{j k}|\},

where the value of $k$ presented in Eq. (1) is adopted as $k =$ 1, 2,…, $K$ and the value of $k$ presented in Eq. (2) is taken as $k =$ 1, 2, …, $K - 1$ .

For the case of $a_{j 0} > a_{j 1} > \dots > a_{j K}$ , the attribute measure functions of single index $μ_{x j k} (t)$ can be determined in the following forms:

3

μ_{x j 1} (t) = \{\begin{array}{l} 0, t < a_{j 1} - d_{j 1}, \\ \frac{t - a_{j 1} + d_{j 1}}{2 d_{j 1}}, a_{j 1} - d_{j 1} \leq t \leq a_{j 1} + d_{j 1}, \\ 1, t > a_{j 1} + d_{j 1}, \end{array}

4

μ_{x j k} (t) = \{\begin{array}{l} 0, t < a_{j k} - d_{j k}, \\ \frac{t - a_{j k} + d_{j k}}{2 d_{j k}}, a_{j k} - d_{j k} \leq t \leq a_{j k} + d_{j k}, \\ 1, a_{j k} + d_{j k} < t < a_{j k - 1} - d_{j k - 1}, \\ \frac{a_{j k - 1} + d_{j k - 1} - t}{2 d_{j k - 1}}, a_{j k - 1} - d_{j k - 1} \leq t \leq a_{j k - 1} + d_{j k - 1}, \\ 0, t > a_{j k - 1} + d_{j k - 1}, \end{array}

5

μ_{x j K} (t) = \{\begin{array}{l} 1, t < a_{j K - 1} - d_{j K - 1}, \\ \frac{a_{j K - 1} + d_{j K - 1} - t}{2 d_{j K - 1}}, a_{j K - 1} - d_{j K - 1} \leq t \leq a_{j K - 1} + d_{j K - 1}, \\ 0, t > a_{j K - 1} + d_{j K - 1} . \end{array}

For the case of $a_{j 0} < a_{j 1} < \dots < a_{j K}$ , the attribute measure functions of single index $μ_{x j k} (t)$ can be determined as follows:

6

μ_{x j 1} (t) = \{\begin{array}{l} 1, t < a_{j 1} - d_{j 1}, \\ \frac{a_{j 1} + d_{j 1} - t}{2 d_{j 1}}, a_{j 1} - d_{j 1} \leq t \leq a_{j 1} + d_{j 1} \\ 0, t > a_{j 1} + d_{j 1}, \end{array},

7

μ_{x j k} (t) = \{\begin{array}{l} 0, t < a_{j k - 1} - d_{j k - 1}, \\ \frac{t - a_{j k - 1} + d_{j k - 1}}{2 d_{j k - 1}}, a_{j k - 1} - d_{j k - 1} \leq t \leq a_{j k - 1} + d_{j k - 1}, \\ 1, a_{j k - 1} + d_{j k - 1} < t < a_{j k} - d_{j k}, \\ \frac{a_{j k} + d_{j k} - t}{2 d_{j k}}, a_{j k} - d_{j k} \leq t \leq a_{j k} + d_{j k}, \\ 0, t > a_{j k} + d_{j k}, \end{array}

8

μ_{x j K} (t) = \{\begin{array}{l} 0, t < a_{j K - 1} - d_{j K - 1}, \\ \frac{t - a_{j K - 1} + d_{j K - 1}}{2 d_{j K - 1}}, a_{j K - 1} - d_{j K - 1} \leq t \leq a_{j K - 1} + d_{j K - 1} \\ 1, t > a_{j K - 1} + d_{j K - 1}, \end{array},

where $k =$ 1, 2,…, $K - 1$ ; and $j =$ 1, 2,…, $m$ .

2.2. Analysis of comprehensive attribute measure

The comprehensive attribute measure $μ_{x k}$ can be calculated by the following form:

9

μ_{x k} = \sum_{j = 1}^{m} ω_{j} μ_{x j k},

where $ω_{j}$ is the weight of the $j$ -th evaluated index and can be derived from the following form:

10

0 \leq ω_{j} \leq 1, \sum_{j = 1}^{m} ω_{j} = 1 .

2.3. Analysis of attribute recognition

To estimate the grade of $x$ presented in assessment grade ( $C_{k}$ ), a comprehensive attribute measure $μ_{x k}$ is used. In general, the assessment set ( $C_{1}$ , $C_{2}$ ,…, $C_{K}$ ) is a ordered set in the attribute comprehensive assessment estimated by using confidence criterion.

The confidence criterion is that ( $C_{1}$ , $C_{2}$ ,…, $C_{K}$ ) is taken as one ordered assessment set of attribute space $F$ . $λ$ is the confidence coefficient with the range of 0.5 to 1, and the value of $λ$ is commonly taken as 0.6-0.7 as suggested in literature [18].

For the case of $C_{1} > C_{2} > \dots > C_{K}$ , if the value of $k_{0}$ can be determined by using Eq. (11), $x$ is considered to be the grade of $C_{k 0}$ :

11

k_{0} = m i n \{k : \sum_{l = 1}^{k} μ_{x l} \geq λ, 1 \leq k \leq K\} .

For the case of $C_{1} < C_{2} < \dots < C_{K}$ , if the value of $k_{0}$ can be determined by using Eq. (12), $x$ is considered to be the grade of $C_{k 0}$ :

12

k_{0} = m a x \{k : \sum_{l = k}^{K} μ_{x l} \geq λ, 1 \leq k \leq K\} .

3. Analyses of attribute assessment index system and its weight

It is well known that the slope stability at tunnel portal is affected by various intricate factors. However, it is difficult to determine each factor. Therefore, the foremost and most influential factors should be selected. In this paper, to estimate the hazard potential during tunnel portal construction, the integrated degree of rock mass, lithological feature, geological structural feature, weathering degree, seismic intensity, gradient, rainfall and construction factors were selected as the indices of the risk assessment. For practical purposes, the landform, strata structure condition, mechanical characteristics of surrounding rock, construction factors and hydrogeological conditions can be considered by using the above-mentioned factors. Therefore, these assessment indices have operability, universality and applicability in the risk assessment for slope stability at tunnel portal.

3.1. Analysis of attribute assessment indices

3.1.1. Integrated degree of rock mass $I_{1}$

The integrated degree of rock mass can be used to depict the development degree of various geological interfaces given priority to with crevice. The quantitative index of the integrated degree of rock mass is an important parameter to assess the engineering properties of rock mass. The integrated degree of rock mass is related to the distribution of structural planes. The structural planes in rock mass greatly affect the rock slope stability, which can reduce the overall intensity of rock mass, and increase the deformability and rheology of rock mass. The intactness index of rock mass $K_{v}$ can reflect the integrated degree of rock mass and can be obtained from the following calculation form:

13

K_{v} = \frac{v_{p m}^{2}}{v_{p r}^{2}},

where $v_{p m}$ and $v_{p r}$ are the compressional wave velocity in rock mass and rock, respectively. The grade division of $K_{v}$ is shown in Table 2.

Table 2Grade division of intactness index in rock mass

Integrated degree	Feature of structural planes	Intactness index $K_{V}$
Unbroken	1~2 groups of structural planes mainly with inclosed stereotype cracks or beddings.	$K_{V} >$ 0.75
Relatively unbroken	2~3 groups of structural planes mainly with stereotype cracks or beddings; the cracks are mostly inclosed, and part of which are micro-open with rare fillers.	0.75 $\geq K_{V} >$ 0.55
Relatively broken	Most 3 groups of irregular structural planes mainly with weathered cracks; the cracks are mostly micro-open and open with many fillers.	0.55 $\geq K_{V} >$ 0.35
Broken	More than 3 groups of structural planes mainly with weathered cracks; the cracks are most opening mode with many fillers	0.35 $\geq K_{V} >$ 0.15
Extremely broken	Disorderly structural planes; creaks are widely open filled with shale or mud debris thickly	$K_{V} \leq$ 0.15

3.1.2. Lithological feature $I_{2}$

The lithology refers to the physical, chemical, hydraulic and mechanical properties of rock. The types and properties of rock are the basic factors affecting slope stability. The slope stability increases with increasing hardness degree and non-deformability of rock under the same condition of slope shape. Meanwhile, the deformation and failure forms of slope are influenced by lithology. The saturated uniaxial compressive strength of rock $R_{c}$ can reflect the hardness degree and lithological feature of rock. The grade division of $R_{c}$ is shown in Table 3.

Table 3Grade division of saturated uniaxial compressive strength

Rock types	Qualitative identification	Saturated uniaxial compressive strength $R_{c}$ / MPa
Extremely hard rock	The rock is hammered with silvery sound and rebound, which is hard to break and has basically no water absorption reaction	≥60
Hard rock	The rock is hammered with relatively silvery sound and slight rebound, which is relatively hard to break and has slight water absorption reaction	30-60
Relatively soft rock	The rock is hammered without silvery sound or rebound, which is easy to break and has deep imprint made by nails after flooding	15-30
Soft rock	The rock is hammered with dumb sound, dents and no rebound, which is easy to shatter and broken by hands after flooding	5-15
Extremely soft rock	The rock is hammered with dumb sound, deeper dents and no rebound, which can be crushed by hands and kneaded into lump after flooding	≤5

3.1.3. Geological structural feature $I_{3}$

The geological structures such as the regional tectonic characteristics, the slope geological folding form, the attitude of rock, and the development characteristics of faults and joints have significant influence on the slope stability. The form and scale of slope deformation and failure are controlled directly by the folded morphology and attitude of rock slope. The faults and crack fracture zones have more obvious influence on the slope failure. According to the historical measurement statistics, the stability degree of geological structure can be divided into five levels from high to low concerning joint spacing $J_{d}$ , i.e., 0.8 m $< J_{d} \leq$ 2.0 m, 0.3 m $< J_{d} \leq$ 0.8 m, 0.2 m $< J_{d} \leq$ 0.3 m, 0.1 m $< J_{d} \leq$ 0.2 m, and 0.01 m $< J_{d} \leq$ 0.1 m.

3.1.4. Weathering degree $I_{4}$

The failure of slope rock is produced continually with time by weathering effect. In general, the weathering of slope rock is related to the composition and structure of rock, temperature, climate conditions and blasting vibration. The weathering speed increases with decreasing rock strength. The weathering coefficient $K_{f}$ can reflect the weathering degree of tunnel rock. The grade division of $K_{f}$ is shown in Table 4.

Table 4Grade division of weathering coefficient

Weathering degree	Field characteristics	Weathering coefficient $K_{f}$
Unweathered	The structure is unchanged; the rock is fresh	$K_{f} >$ 0.9
Slightly weathered	The structure and mineral color are basically unchanged; some fractures have iron and manganese rendering	0.9 $\geq K_{f} >$ 0.8
Weakly weathered	The structure is partially destroyed; the mineral color has obvious change; the weathering minerals or weathering layers appear in the fissure surface	0.8 $\geq K_{f} >$ 0.3
Strongly weathered	The structure is mostly destroyed; the mineral color has obvious change	0.3 $\geq K_{f} >$ 0.1
Completely weathered	The structure is completely destroyed; the mineral components are basically weathered into earthy aggregate	$K_{f} \leq$ 0.1

3.1.5. Seismic intensity $I_{5}$

The tensile fracture and relaxation of structural planes in slope rock can be caused due to the seismic vibration. The influence degree of earthquake on slope failure is mainly depended on the seismic intensity. Generally, seismic intensity is the long-term index of operating period which can be revised to enlarge its weight in the evaluation because of the free surface effect and stress field redistribution in the excavation process. The seismic intensity is divided into five levels as follows: $I_{5} <$ 3, $I_{5} =$ 3-5, $I_{5} =$ 5-7, $I_{5} =$ 7-8, and $I_{5} >$ 8.

3.1.6. Gradient $I_{6}$

The relationship between gradient and slope stability is inevitable, i.e., the stability of slope decreases with increasing gradient and increases with decreasing gradient. According to the existing engineering statistics, the grade division of gradient is summarized as below: gentle slope (0°-15°), moderate slope (15°-30°), abrupt slope (30°-45°), steep slope (45°-60°) and cliff (60°-90°).

3.1.7. Rainfall factor $I_{7}$

The influence of water on the slope stability at tunnel portal is many-sided including precipitation, rainfall intensity and water infiltration. The rain can effectively increase the ground water infiltration, loading and weathering degree of slope and reduce the shear strength, which may cause the landslide, mud-rock flow and collapse of rock.

3.1.8. Construction factor $I_{8}$

The engineering disturbances are the direct inducing factors of slope unstability at tunnel portal, such as improper excavation method, untimely supporting structure and non-standard monitoring measure operation. The construction factor is influenced by the construction unit level. Therefore, the technology and management of construction unit are selected for the simplified analysis with grade division, as shown in Table 5.

Table 5Grade division of construction management and technical level

Grade	Definite description
Ⅰ	Excellent credit; rich construction experience; strong technical force
Ⅱ	Favorable credit; relatively rich construction experience; relatively strong technical force
Ⅲ	Common credit, construction experience and technical force
Ⅳ	Relatively poor credit, construction experience and technical force
Ⅴ	Poor credit; serious insufficient construction experience and technical force

3.2. Grading criteria of attribute assessment indices

Based on above-mentioned analysis with grade division, the attribute assessment indices of slope stability at tunnel portal are divided into five grades, as shown in Table 6.

Table 6Indices and criteria for risk assessment of slope stability at tunnel portal

Risk grade	$K_{V}$	$R_{c}$ / MPa	$J_{d}$	$K_{f}$	Seismic intensity	Gradient / °	Annual precipitation	Construction management and technical level
I Stable	$K_{V} >$ 0.75	200-300	0.8-2.0	$K_{f} >$ 0.9	<3	<15	0-400	Excellent
II Relatively stable	0.75 $\geq K_{V} >$ 0.55	150-200	0.3-0.8	0.9 $\geq$ $K_{f} >$ 0.8	3-5	15-30	400-700	Favorable
III Basically stable	0.55 $\geq K_{V} >$ 0.35	100-150	0.2-0.3	0.8 $\geq$ $K_{f} >$ 0.3	5-7	30-45	700-1000	Common
IV unstable	0.35 $\geq K_{V} >$ 0.15	50-100	0.1-0.2	0.3 $\geq$ $K_{f} >$ 0.1	7-8	45-60	1000-1500	Poor
V Extremely unstable	$K_{V} \leq$ 0.15	0-50	0.01-0.1	$K_{f} \leq$ 0.1	>8	>60	>1500	Extremely poor

3.3. Attribute measure functions of single index

To establish the attribute measure functions concerning single index (see Table 7 in Appendix), the data of seven indices ( $I_{1}$ - $I_{7}$ ) shown in Table 6 are consistent with the requirements of Table 1. The attribute measure of qualitative index $I_{8}$ is expressed by 0 or 1 [19].

3.4. Weights of assessment indices

The importance degree of assessment object can be reflected by the corresponding index weight of risk assessment for slope stability at tunnel portal. Expert scoring method, binomial coefficient method and analytic hierarchy process were commonly used to determine the weight. The determination on the weight by using the analytic hierarchy process can be summarized as: (1) the formation of judgment matrix; (2) the solution of importance order; and (3) consistency check. The rationality of weight solution is greatly affected by the scale determination in formation of judgment matrix. The 10/10-18/2 scale method with well uniformity was adopted in this paper. The unit feature vector (weights) $ω$ corresponding to the maximum eigenvalue $λ_{m a x}$ of judgment matrix derived from square root method can be obtained. The consistency check of judgment matrix was then carried out. For the case of the consistency ratio of judgment matrix $C_{R} <$ 0.10, the judgment matrix can be considered to have well consistency with reasonable weighted assignment.

The solved unit feature vector of assessment indices is $ω =$ (0.213, 0.140, 0.139, 0.095, 0.092, 0.138, 0.093, 0.090), the maximum eigenvalue $λ_{m a x} =$ 8.000, and the consistency ratio of judgment matrix $C_{R} =$ 2.319×10^-5 < 0.10, suggesting the proposed weights can satisfy the consistency check.

4. Project applications

Jianfangcun Tunnel of Cheng-Lan Railway is located in Songpan county of Sichuan province, China, and the whole length and maximum burial depth of which are about 3868 m and 600 m, respectively. The roadbed at exit section of Jiefangcun Tunnel (D1K191+048~D1K191+123) is located in the eastern edge of qinghai-tibet plateau, and the whole length, maximum excavated depth and maximum filling height are 75 m, 14.6 m and 13.25 m, respectively. The unfavorable geologies within the section are landslides, rock heap, dangerous rock rockfalls, bedding slope, cavities, high ground stress, high geotemperature, sandy soil liquefaction.

The notable geological characteristics of tunnel zone were summarized as below: (1) the terrain cutting was extremely strong; (2) the tectonic condition was extremely intricate and active; (3) the lithological condition was extremely weak and broken; (4) and the Wenchuan earthquake effect was extremely significant. Moreover, the risks of high crustal stress, high seismic intensity and high geological disaster were potential in rock mass. The mountain slope of tunnel roof was abrupt with loose lithology and rudimentary vegetation. The rocks in tunnel area were sandstone and phyllite with development of joint.

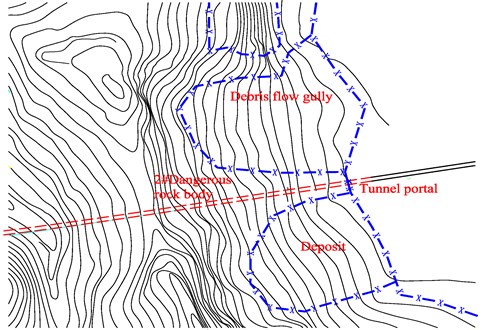
The attribute recognition model of risk assessment for slope stability at tunnel portal was adopted to evaluate the slope stability of portal section D1K191+035 of Jiefangcun Tunnel (see Fig. 1). The diagram of tunnel geography is shown in Fig. 2.

Fig. 1Realistic picture of Jiefangcun Tunnel

4.1. Calculation for attribute measures of single index and comprehensive indices

Integrated degree of rock mass is taken as broken with its intactness index $K_{V} =$ 0.22; Lithological feature is soft for the saturated uniaxial compressive strength of the in-site rock sample $R_{c} =$ 5.47 MPa. For geological structural feature and weathering degree, the average joint spacing $J_{d}$ is 0.18 m by in-site measurement while the surrounding rock is completely weathered. Seismic intensity is identified as 8 according to the historical geological structure analysis. The average gradient of the slop at the tunnel exit area is 57°.

Fig. 2Diagram of tunnel geography

Based on the specimen data (see Table 8) and the attribute measure functions of single index (see Table 7 in Appendix), the attribute measures of single index can be calculated. The comprehensive attribute measures of specimen can be calculated by Eq. (9), as shown in Table 8.

Table 8Calculation table of attribute measures

Indices	Measured value	Attribute measures
Indices	Measured value	$C_{1}$	$C_{2}$	$C_{3}$	$C_{4}$	$C_{5}$
$I_{1}$	0.22	0	0	0	0.3	0
$I_{2}$	5.47 MPa	0	0	0.59	0.41	0
$I_{3}$	0.18 m	0	0.	0.3	0.7	0
$I_{4}$	0.09	0	0	0	0.4	0.6
$I_{5}$	8	0	0	0	0.5	0.5
$I_{6}$	57°	0	0	0	0.68	0.32
$I_{7}$	720 mm	0	0.43	0.57	0	0
$I_{8}$	Excellent	1	0	0	0	0
Comprehensive attribute measures		0.090	0.040	0.177	0.396	0.147

4.2. Analysis of attribute recognition

The order of assessment set ( $C_{1}$ , $C_{2}$ , $C_{3}$ , $C_{4}$ , $C_{5}$ ) is taken as $C_{1} > C_{2} > C_{3} > C_{4} > C_{5}$ [19]. When the value of $λ$ is adopted as 0.70, Eq. (11) can be written as the following form:

14

k_{0} = m i n \{k : \sum_{l = 1}^{k} μ_{x l} \geq 0.70,1 \leq k \leq 5\} .

The stability grade of slope at Jiefangcun Tunnel portal is $C_{4}$ provided with rather high risk. The results derived from the extension assessment method [7] are consistent with the results in this paper. The rationality and feasibility of application of attribute mathematics theory in the risk assessment for slope stability at tunnel portal is verified.

The method used in this paper can solve the deviation of the geological qualitative analysis caused by human subjectivity. The influence of human subjectivity on selection of risk factors and level division is reduced to some extent based on the standard of hydrogeology and engineering geology and the experience of exports consultation. This method of risk evaluation of slope instability, considering the impact of excavation tunnel portal, could be used to make scheme comparison of tunnel portal construction and slope protection in the investigation stage; in the construction stage, appropriate risk treatment programs or measures could also be developed in accordance with the evaluation results to achieve the purpose of disaster prevention and mitigation, early warning and safe construction.

4.3. Tracking and treatments for construction risk of tunnel portal

To make risk solutions and enhance monitoring for avoiding or reducing loses, the risk assessment was carried out in practice. The tracking and treatment in tunneling process of Jiefangcun Tunnel were as follows:

The cracks were produced at many places at the surface, slope and primary supporting of tunnel with small-scale collapse after the portal excavation of Jiefangcun Tunnel (see Fig. 3). After the risk analysis and assessment, the following treatments were adopted to guarantee the construction safety: (1) the grouting reinforcement towards surrounding rock of tunnel portal was used; (2) the advanced grouting with small pipe was added to reinforce the forward surrounding rock; (3) the surface of tunnel ceiling was covered with striped cloth, and the net-suspended spraying was conducted to close the cracks; (4) the bias open cut tunnel was built; and (5) the temporary invert was added.

Fig. 3Tracking for construction risk of tunnel portal

a)

b)

c)

5. Conclusions

In the present paper, to ensure the construction safety of tunnel, the attribute recognition model of risk assessment for the slope stability at tunnel portal was established by using attribute mathematics theory. The integrated degree of rock mass, lithological feature, geological structural feature, weathering degree, seismic intensity, gradient, rainfall and construction factors were selected as the indices of the risk assessment for the stability slope at tunnel portal with grading criteria of each index. Moreover, the weights of the assessment indices were determined by the judgment matrix constructed from analytic hierarchy process. The attribute measurement functions were used to compute attribute measurement of single index and synthetic attribute measurement. The identification and classification of risk assessment for the slope stability at tunnel portal were assessed using the confidence criterion. For practical purposes, the stability of slope located in portal of an actual Tunnel, i.e., Jiefangcun Tunnel in Cheng-Lan Railway, was evaluated based on the previously established attribute recognition model. The corresponding risk treatment measures were then proposed based on the assessment results and monitor results to ensure the construction safety of tunnel portal.

References

Barisone G., Pelizza S., Pigorini B. Italian Experience with Tunnel Portalsin Difficult Ground. Eurotunnel, Basilea, 1983.

Search CrossRef
Giani G. P. Rock Slope Stability Analysis. Balkema, Rotterdam, 1992.

Search CrossRef
Quek S. T., Leung C. F. Reliability-based stability analysis of rock excavations. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, Vol. 32, Issue 6, 1995, p. 617-620.

Publisher
Lee I. M., Park J. K. Stability analysis of tunnel keyblock: a case study. Tunnelling and Underground Space Technology, Vol. 15, Issue 4, 2000, p. 453-462.

Publisher
Peila D., Pelizza S. Criteria for technical and environmental design of tunnel portals. Tunnelling and Underground Space Technology, Vol. 17, 2001, p. 335-340.

Publisher
Søen Degn Eskesen, Tengborg Per, Jøgen Kampmann Guidelines for tunneling risk management: International tunneling association, working group No. 2. Tunnelling and Underground Space Technology, Vol. 19, 2004, p. 217-237.

Publisher
An Yong-lin, Peng Li-min, Wu Bo Comprehensive extension assessment on tunnel collapse risk. Journal of Central South University, Vol. 42, Issue 2, 2011, p. 514-520.

Search CrossRef
Hwang Jin Hung, Lu Chih Chieh Seismic capacity assessment of old Sanyi railway tunnels. Tunnelling and Underground Space Technology, Vol. 22, 2007, p. 433-449.

Publisher
Li De-yi, Liu Dong-bo A Fuzzy Prolog Database System. John Wiley and Sons, New York, 1990.

Search CrossRef
Li Zhi-lin, Wang Xin-hua, Xie Li-zhao Risk evaluation and comprehensive geological prediction based on fuzzy wavelet neural network during tunneling in karst area. Electronic Journal of Geotechnical Engineering, Vol. 17, 2012, p. 2155-2167.

Search CrossRef
Panou K. D., Sofianos A. I., Kaliampakos D. The use of the analytic hierarchy process for the selection between a road tunnel and an open cut in an environmentally sensitive area. Proceedings of the 3rd Hellenic Conference in Geotechnical Engineering, Vol. 2, 1996, p. 351-358.

Search CrossRef
Panou K. D., Sofianos A. I. A fuzzy multicriteria evaluation system for the assessment of tunnels vis-à-vis surface roads: theoretical aspects – Part I. Tunnelling and Underground Space Technology, Vol. 17, 2002, p. 195-207.

Publisher
Song Ki-il, Cho Gye-chun, Chang Seok-bue Identification, remediation, and analysis of karst sinkholes in the longest railroad tunnel in South Korea. Engineering Geology, Vols. 135-136, 2012, p. 92-105.

Publisher
Zhou Jian-kun, Wu Jian Fault tree analysis of the collapse risk in rock highway tunnel. Chinese Journal of Underground Space and Engineering, Vol. 4, Issue 6, 2008, p. 991-998.

Search CrossRef
Wang Yan, Huang Hong-wei, Xue Ya-dong Risk analysis of collapse for tunnels constructed by drill and blast method. Journal of Shenyang Jianzhu University (Natural Science), Vol. 25, Issue 1, 2009, p. 23-27.

Search CrossRef
Wang Zheng-zheng, Zhang Zhe, Gao Bo, Shen Yu-sheng Factors of seismic damage and fuzzy synthetic evaluation on seismic risk of mountain tunnel portals. Journal of Central South University (Science and Technology), Vol. 43, Issue 3, 2012, p. 1122-1130.

Search CrossRef
Xu Wei-ya, Jiang Zhong-ming, Shi An-chi Slope stability analysis using fuzzy sets theory. Chinese Journal of Geotechnical Engineering, Vol. 25, Issue 4, 2003, p. 409-413.

Search CrossRef
Cheng Qian-sheng Attribute recognition theoretical model with application. ACTA Scicentiarum Naturalum Universitis Pekinesis, Vol. 33, Issue 1, 1997, p. 12-20.

Search CrossRef
Wen Chang-ping, Yang Guo-lin The seismic stability evaluation of the rock and soil slope based on the attribute mathematical theory. China Railway Science, Vol. 31, Issue 5, 2010, p. 8-14.

Search CrossRef

Cited by

Analysis of Loose Surrounding Rock Deformation and Slope Stability at Shallow Double-Track Tunnel Portal: A Case Study

Chenguang Li | Huanyu Zheng | Zhaojian Hu | Xiaofei Liu | Zhen Huang

(2023)

Coupling Analysis of Tunnel Construction Safety Risks Based on N-K Model and SD Causality Diagram

Mengyao Zhang | Deming Yu | Tianyu Wang | Can Xu

(2023)

Environmental Risk Source Analysis and Classification of Zones: Subway Construction

(2023)

2023 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC)

Xinglong Feng | Bian Li | Zengrong Li | Shuang Zhang | Heng Huang

(2023)

2022 International Conference on Cloud Computing, Big Data and Internet of Things (3CBIT)

Qingqing Kong | Yong Ding | Xiaoling Liu | Zhibin Cao

(2022)

A multi-index evaluation method for rockburst proneness of deep underground rock openings with attribute recognition model and its application

(2022)

Safety Evaluation of Subway Tunnel Construction under Extreme Rainfall Weather Conditions Based on Combination Weighting–Set Pair Analysis Model

Ping Liu | Yu Wang | Tongze Han | Jiaming Xu | Qiangnian Li

(2022)

Collapse risk assessment of deep-buried tunnel during construction and its application

(2021)

Risk assessment of highway structures in natural disaster for the property insurance

(2020)

Study on slope stability due to the influence of excavation of the high-speed rail tunnel

Qian Zhang | Jing Wang | Wenyu Wang | Songsong Bai | Peng Lin

(2019)

Development and Application of Ancient Timber Buildings Structural Condition Assessment Model Based on a Fuzzy Matter-Element Model that Includes Asymmetric Proximity

Zhongwei Gao | Donghui Ma | Wei Wang | Xiaodong Guo | Qingzi Ge

(2018)

About this article

Received

23 October 2016

Accepted

04 May 2017

Published

30 June 2017

SUBJECTS

Seismic engineering and applications

DOI

https://doi.org/10.21595/jve.2017.17869

Keywords

tunnel portal

slope stability

risk assessment

attribute recognition

Acknowledgements

This work was supported by the National Natural Science Foundation of China (51609138). Great appreciation goes to the editorial board and the reviewers of this paper.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 08 03

Determining tunnel stability across fault zones under seismic loading based on load/unload response ratio theory

Qiang Hui, Feng Gao, Xukai Tan, Dongmei You

Research article

2023 04 09

Dynamic damage and response characteristics of the tunnel by FEM modeling and field trials

Xianjun Zheng, Tingyao Wu, Chao Wu, Xiaoqin Wang

Research article

2022 11 18

Simulation analysis on seismic dynamic response of pile supported tunnels in deep backfill area of soil-rock mixture

Guoshun Shen, Yuanhao Lou, Jianguo Wu, Xiaoguang Jin, Yunchuan Xue

Research article

2020 11 15

Tunnel surrounding rock stability prediction using improved KNN algorithm

Shuai Huang, Qingjie Qi, Jianzhong Liu, Wengang Liu

Q. Zhang, J.- Wang, and H.- Zhang, “Attribute recognition model and its application of risk assessment for slope stability at tunnel portal,” Journal of Vibroengineering, Vol. 19, No. 4, pp. 2726–2738, Jun. 2017, https://doi.org/10.21595/jve.2017.17869

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.17869
UR  - https://doi.org/10.21595/jve.2017.17869
TI  - Attribute recognition model and its application of risk assessment for slope stability at tunnel portal
T2  - Journal of Vibroengineering
AU  - Wang, Jing-chun
AU  - Zhang, Qian
AU  - Zhang, Hai-xia
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 2726-2738
IS  - 4
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Wang_2017,
	doi = {10.21595/jve.2017.17869},
	url = {https://doi.org/10.21595/jve.2017.17869},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {4},
	pages = {2726--2738},
	author = {Jing-chun Wang and Qian Zhang and Hai-xia Zhang},
	title = {Attribute recognition model and its application of risk assessment for slope stability at tunnel portal},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]J. Wang, Q. Zhang, and H. Zhang, “Attribute recognition model and its application of risk assessment for slope stability at tunnel portal,” Journal of Vibroengineering, vol. 19, no. 4, pp. 2726–2738, Jun. 2017, doi: 10.21595/jve.2017.17869.

Copy IEEE

Copied to clipboard!

Wang, Jing-chun, Qian Zhang, and Hai-xia Zhang. “Attribute Recognition Model and Its Application of Risk Assessment for Slope Stability at Tunnel Portal.” Journal of Vibroengineering 19, no. 4 (June 30, 2017): 2726–38. https://doi.org/10.21595/jve.2017.17869.

Copy Chicago

Copied to clipboard!

Attribute recognition model and its application of risk assessment for slope stability at tunnel portal

Abstract

1. Introduction

2. Attribute recognition model of risk assessment for slope stability at tunnel portal

2.1. Analysis of single-index attribute measure

2.2. Analysis of comprehensive attribute measure

2.3. Analysis of attribute recognition

3. Analyses of attribute assessment index system and its weight

3.1. Analysis of attribute assessment indices

3.1.1. Integrated degree of rock mass I1

3.1.2. Lithological feature I2

3.1.3. Geological structural feature I3

3.1.4. Weathering degree I4

3.1.5. Seismic intensity I5

3.1.6. Gradient I6

3.1.7. Rainfall factor I7

3.1.8. Construction factor I8

3.2. Grading criteria of attribute assessment indices

3.3. Attribute measure functions of single index

3.4. Weights of assessment indices

4. Project applications

4.1. Calculation for attribute measures of single index and comprehensive indices

4.2. Analysis of attribute recognition

4.3. Tracking and treatments for construction risk of tunnel portal

5. Conclusions

References

Cited by

About this article

Related Articles

3.1.1. Integrated degree of rock mass $I_{1}$

3.1.2. Lithological feature $I_{2}$

3.1.3. Geological structural feature $I_{3}$

3.1.4. Weathering degree $I_{4}$

3.1.5. Seismic intensity $I_{5}$

3.1.6. Gradient $I_{6}$

3.1.7. Rainfall factor $I_{7}$

3.1.8. Construction factor $I_{8}$