Journal of Vibroengineering
Browse Journal
Submit article
Journal of Vibroengineering Browse Journal Volume 19, Issue 8 Research article
Published: 31 December 2017
Check for updates

Simulation analysis on inner flow field and optimization design of air knife

Jian Qing Chen1
Ke Chen2
Xian Ming Chen3
1School of Engineering, Huzhou University, Huzhou, 313000, China
1, 2School of Mechanical Engineering, Hefei University of Technology, Hefei, 230009, China
3School of Mechanical and Automotive Engineering, Zhejiang University of Water Resources and Electric Power, Hangzhou, 310018, China
Corresponding Author:
Jian Qing Chen
Cite the article Download PDF
Views 1296
Reads 723
Downloads 3201
WoS Core Citations 3
CrossRef Citations 3

Abstract

This paper conducted a parametric modeling for air knife structure in a printing factory, used HYPERMESH software to divide the meshes of air model and combined with actual conditions to define various boundary conditions in the inner flow field of air knife. Meanwhile, this paper adopted fluid dynamics software Fluent to conduct numerical simulation for the internal airflow of air knife, obtained the distribution regulation of flow field, conducted a parametric modeling for air knife structure under many internal structural proposals through ANSYS design module based on the simulation computational result, conducted optimization design for the position of guide plates, the number of outlets and the size of return air tank in the detailed structure in the air knife in order to determine specific dimension parameters and optimal proposals. Based on the computational results of simulation, this paper found that the original air knife structure had a non-uniform flow field and low velocity at the inlet and outlets. With the increase of length of air knife, the velocity of the middle outlet reduced to zero and did not have obvious effects any more. Guide plates in the air knife had a great influence on the inner flow field of air knife. Through optimization design, the inner flow field of air knife became uniform when there was only one guide plate. When the guide plate was close to the front end of the air knife, the inner flow field of air knife was relatively uniform and velocity at the inlet and outlets was relatively high. This paper conducted a model design for air knives with different structural types and determined proposal 4 as the optimal design through repeated analysis. The design method in this paper could provide guidance for studying and designing air knife structures in the aspect of technological approach and theory.

1. Introduction

At present, air knives are an important equipment used for the deep and fine processing of products [1]. Air knives are widely applied in a variety of industries including automobiles, electrons, chemistry, metal processing, packaging, paper printing and so on. Featured with low cost, uniform airflow, simple structure, easy installation, effective reduction of energy loss and so on, air knives are favored by many people [2].

Air knives are mainly used for a variety of surface engineering fields, drying, preheating, coating and other processes [3-5]. The main structure of air knives is usually made of aluminum alloy or stainless steel. Air knives blow pure compressed air into the cavity through a fan. Through the rectification effect of air knives, a strong air curtain will appear at the outlet. Air knives can be used for the surface cleaning, drying and air cooling of equipment or products, such as glass panels, electronic circuit boards and high-grade metal plates. With the development of science and technology, air knives are applied in more high-end fields, like production, research and development, spraying and coating of optical lenses and preheating and temperature control of sheet products [6-10].

There are various kinds of air knives. According to different application fields, air knives are again divided into different types, such as strong-wind air knives, bending-type air knives and circular-type hot air knives. However, their processes have common points. In short, air knives blow pure compressed air into the cavity through a fan. Air usually experiences rectification, filtration and other processes in the air knife, flows out from a long rectangular outlet and forms a strong air curtain at the outlet. However, air knives are difficult to control in the process of actual use. Air only has a single inlet. Unstable high pressure airflow in the cavity of air knife leads to unstable airflow at the outlet. In particular, changes in inlet boundary conditions like flux and position will have an impact on the flow field distribution and stability of airflow at the outlet side to a certain degree. To ensure uniform and stable airflow and air pressure at the outlet of air knife, it is usually necessary to add guide plate structure in the air knife.

A number of researchers have adopted finite element simulation software to study the flow field distribution in the air knife to further ensure the accuracy and stability of the air knife [10]. Gosset [11] analyzed the influence of nozzle shape of air knife on its flow field and simulated flow field in the cavity of air knife, but they failed to design the outlet. Ahn [12] studied the influence of internal guide plates on the flow field of air knife and conducted a simulation analysis on the two-dimensional flow field of air knife which was greatly different from the inner flow field distribution of actual three-dimensional air knife structure. Farkas [6] analyzed the flow field of air knife of glass washers, and he thought that Dumur air knife adopted a rectangular cross-section and produced a large airflow vortex, which hindered airflow and thus resulted in energy loss and the vibration of air knife. However, their conclusions were obtained based on the computation of two-dimensional models. They did not conduct an analysis on three-dimensional flow fields. Liu [7] used finite element software to conduct a numerical simulation studies and experiments on the inner flow field of air knife of glass washers and pointed out that maximum wind velocity decreased when the outlet width of air knife increased. However, he only computed two-dimensional flow fields and failed to conduct an analysis on three-dimensional models. Choi [13] preliminarily discussed a variety of air knifes, applied the basic theory of fluid dynamics to analyze air knife structure and pointed out that effective air filtration at the inlet of high pressure fans brought a lot of benefits to the processing quality of air knife. Albanesi [14] adopted the inverse analysis and designed the air knife structure of composite materials. However, he did not further optimize air knife structure. Therefore, such kind of air knife structures could not be applied to actual factories. Wang [15] conducted local optimization design for air knife structure using finite element method and genetic algorithm. However, optimization design was only conducted for the internal guide plates of air knife and optimization design was not conducted for other structures of air knife. Lee [16] conducted a simulation and comparative analysis on the flow field of air knife structures with different materials. However, optimization design for the structure, size and shape of air knife was not involved.

The stability of flow field in the air knife, air flux and the uniformity of wind velocity at the outlet of air knife are several important indicators for measuring the quality of air knife [17, 18]. However, people still need to further conduct studies on the principle of air knives. The flow field distribution in the cavity of air knives is not still clear. There are not sufficient studies on the flow and temperature distribution of air. The structure of rectifier tank in the air knife has to depend on production experience and experiments. Few studies have been conducted on the aerodynamic of air knife structure. At the outlet of air knife, airflow direction and velocity are not very uniform. Airflow velocity is too high in the middle of air knife and too low at sides. There are large differences between maximum velocity and minimum velocity, which affects the surface quality of fine processing products. In addition, airflow may also lead to the vibration of the air knife after flowing through air knife at high speed, which further affects the uniformity and stability of flow field [19-21].

For solving the mentioned problems, this paper conducted a parametric modeling for air knife and air model in a printing factory, used HYPERMESH software to divide the meshes of air model and combined with actual conditions to define various boundary conditions in the inner flow field of air knife. In addition, this paper adopted Fluent to conduct numerical simulation for the internal airflow of air knife, obtained the distribution regulation of flow field, and conducted optimization design for guide plates, return air tank and size in the air knife based on the computational result in order to effectively reduce the problem of non-uniform airflow at the outlet of air knife.

2. Computation and design theory of flow field of air knife

2.1. Computation theory of flow field of air knife

Fluid motion follows the law of mass conservation, momentum conservation and energy conservation. Firstly, fluid satisfied the requirements of mass conservation in the process of flowing. Its differential equation was expressed as:

1
∂ρ∂t+∂ρux∂x+∂ρuy∂y+∂ρuz∂z=0,

wherein, ux, uy, uz represented velocity components in the X, Y and Z direction of space coordinate. t was time variable. ρ was fluid density.

In the process of flowing, fluid still needed to satisfy momentum equation. Momentum equations in various directions were expressed as:

2
∂ρux∂t+∇⋅ρux=∂p∂x+∂τxx∂x+∂τxy∂y+∂τxz∂z+ρfx,∂ρuy∂t+∇⋅ρuy=∂p∂y+∂τyx∂x+∂τyy∂y+∂τyz∂z+ρfy∂ρuz∂t+∇⋅ρuz=∂p∂z+∂τzx∂x+∂τzy∂y+∂τzz∂z+ρfz,,

wherein, f stood for the mass force of fluid. fx, fy and fz represented mass forces respectively in three directions. p was pressure at the spatial point of fluid. τ was viscous stress under the viscous effect of fluid molecules. Fluid needed to satisfy the equation of total energy conservation in the process of flowing:

3
∂ρE∂t+∇ρE+p=∇keff∇T-∑jhjJj+τeff+Sh,

wherein, hj was the enthalpy of component j. keff was an effective coefficient of thermal conductivity. Jj was the diffusive flux of component j. Sh was a volume heat source item. E was the total energy of fluid and the sum of internal energy, kinetic energy and potential energy.

Pressure in the cavity of air knife structure has an influence on the acceleration and velocity of air. Therefore, it is necessary to ensure the uniform and stable distribution of pressure at the outlet in order to guarantee the uniform distribution of flux at the outlet. This paper adopted the Fluent to conduct simulation solution for the flow field of air knife. As a general CFD solver based on finite element volume method, the software Fluent can solve the flow field problem of incompressible or compressible fluid and obtain high accuracy. For general air knife structures, airflow in the working cavity of air knife is in a turbulent state. Therefore, k-ε turbulence model and STARDAND solver were selected from Fluent to solve the inner flow field distribution of air knife.

2.2. Optimization design theory of air knife

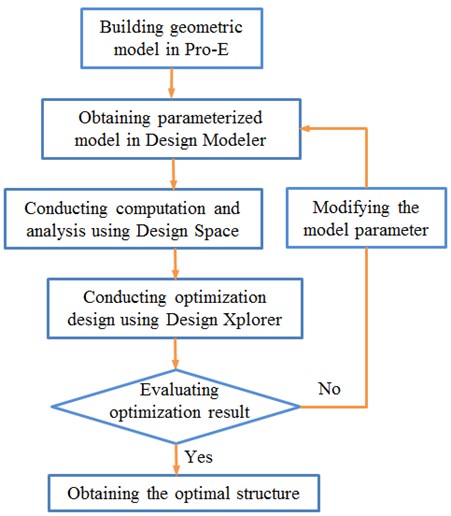
This paper adopted ANSYS to conduct an optimization design for air knife structure. ANSYS optimization design contained Design Modeler module, Design Space module and Design Xplorer module. Detailed process was as follow:

1. A geometric model was built firstly, and it was then imported into Design Modeler. An analysis was conducted through Design Space and then optimization design was conducted using Design Xplorer.

2. The optimal combination satisfying design conditions in Design Xplorer was generated. Monte Carlo method was usually adopted to extract design parameters and analysis samples according to the target to be solved, and further an analysis was conducted to obtain all response surfaces of design space.

3. The data after optimization design was passed back to Design Modeler, repeated analysis and the process were conducted for many times.

4. The best result conforming to the target to be solved and optimized in the end was obtained through the optimization algorithm of software.

The optimization design module of ANSYS could greatly reduce design time; improve the accuracy and efficiency of design products and save design cost. As a result, the air knife structure in this paper adopted ANSYS to conduct an optimization design. The flow diagram of optimization design was shown in Fig. 1.

Fig. 1Flow diagram of the optimization design

Flow diagram of the optimization design

3. Finite element model of air knife

3.1. Geometric model of air knife

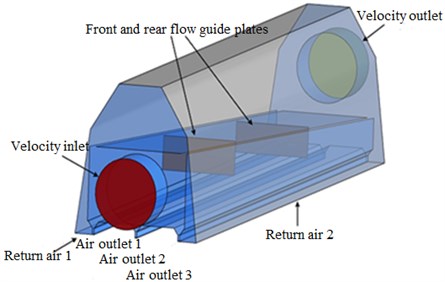
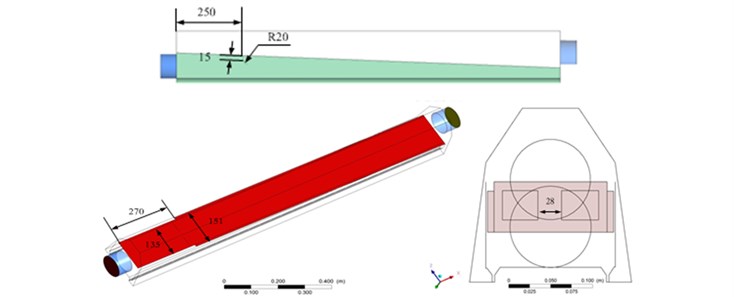
Fig. 2 showed the original air knife model studied in this paper. The air knife model in this paper is usually used for the drying of papers on the printing factories. The air knife was 1000 mm long. There was a velocity inlet with a diameter of 97 mm in the front of the air knife; there was a velocity outlet with a diameter of 96 mm in the rear of the air knife. There was a return air inlet at left and right sides of the structure. The backlash of the return air inlet was 7 mm wide. There were three air outlets which were 3 mm wide at the bottom of the structure. There were two vertical guide plates whose size was 100 mm×50 mm in the front and rear in the air knife.

Fig. 2The geometric model of air knife

The geometric model of air knife

3.2. Mesh division of air knife

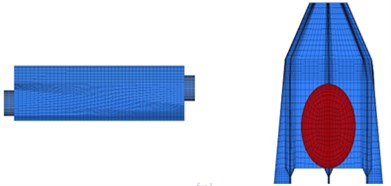
The key analysis of air knife focused on the air model of inner space. HYPERMESH software was adopted to divide the meshes of the model, as shown in Fig. 3. As meshes at both ends of the air knife might generate vortexes, meshes at ends, inlet and outlet of the air knife were divided finely to obtain more accurate results. In addition, hexahedral meshes were adopted to divide the model in order to ensure computational accuracy and save computational resources. There are 360056 elements and 390788 nodes. The material of the air knife is steel, so the Elastic Modulus is 2.1e11Pa, density is 7800 kg/m3, and Poisson’s ratio is 0.3.

Fig. 3Mesh model of air knife

Mesh model of air knife

3.3. Boundary conditions and computational parameters

Airflow was in a turbulent state in the air knife. Therefore, k-ε turbulence model was required. The inlet velocity of the model was 30 m/s. Outlet boundary was set as Outflow. The wall adopted no-slip wall boundary. The air knife selected air as its fluid medium. The material properties of air were shown in Table 1.

Table 1Parameters of air as a medium

Material
Density (kg/m3)
Viscosity coefficient (kg/m·s)
Temperature (°C)
Air
1.225
1.5E-5
20

4. Computational result and analysis of the original air knife model

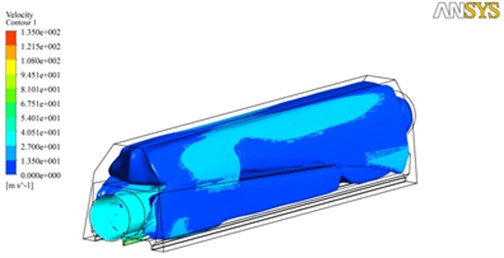
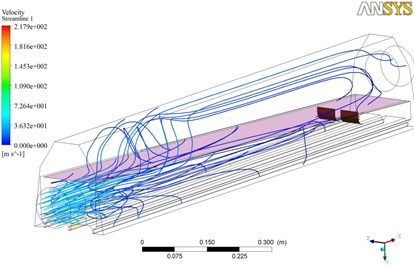
Fluent solver was adopted to solve the air knife model to obtain its three-dimensional trace and the simulation result of two-dimensional trace in the center symmetry plane, as shown in Fig. 4.

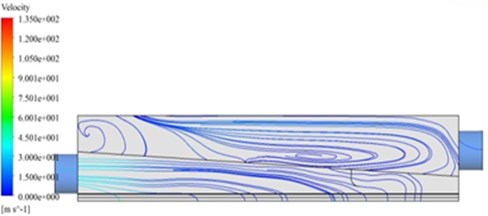
As shown in Fig. 4, air entered from the inlet and flew out from the outlet and return air inlet through two guide plates in the lower cavity. It could be seen from the figure that air generated an effective vortex behind the first guide plate after flowing through the guide plate. Air velocity dramatically decreased. Air continued to flow. After flowing through the second guide plate, air did not generate a vortex behind the guide plate due to the decrease of air velocity. Most of air flew out from the return air inlet stably. Only a small part of air flew into the upper cavity of the air knife from the gap between upper and lower cavities. Due to the high pressure area at the front end of the inlet, a part of air flew out from the return air inlet and a part of flew into the upper cavity from the gap between upper and lower cavities after air flew through the first guide plate. Finally, air flew out from the outlet.

Fig. 4The inner flow field of the original air knife model

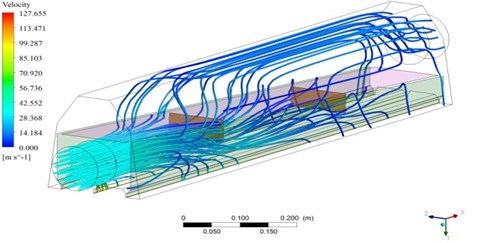
The inner flow field of the original air knife model

a) Three-dimensional trace

The inner flow field of the original air knife model

b) Two-dimensional trace

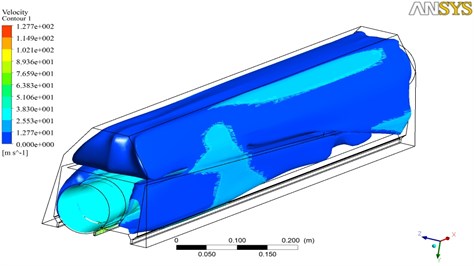
The inner flow field of the original air knife model

c) Contours of flow velocity

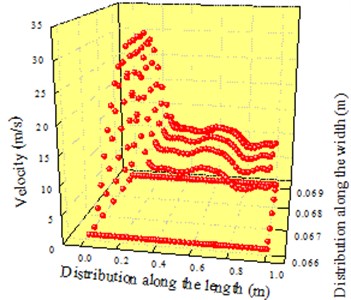
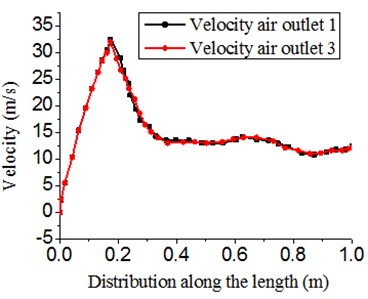
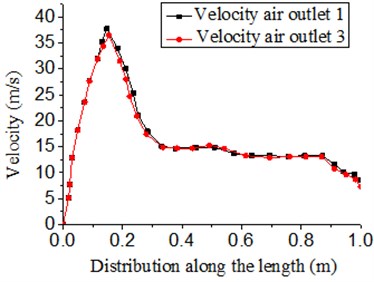
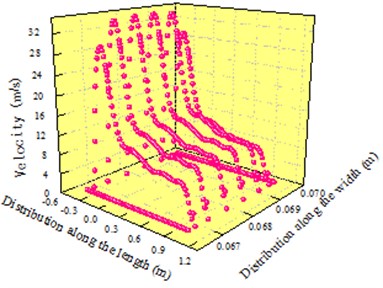
Fig. 5 showed three-dimensional and two-dimensional distribution of velocity at outlet 1 and 3 respectively. Though the model was symmetrical, outlet 1 was not exactly the same with outlet 3 in the velocity distribution. Due to the influence of boundary layers on both sides, velocity distribution close to the boundary layer was basically zero. Fig. 5(a) presented the velocity distribution of air with different widths. Fig. 5(b) showed the velocity distribution which was mapped and transformed from Fig. 5(a) in the two-dimensional plane in order to express the distribution situation of air with the different length (The three-dimensional and two-dimensional distribution of velocity at the outlet would appear many times later, which had the same purpose).

Along the direction of length, it could be seen that velocity peak was at the position which was 210 mm away from the inlet. The peak velocity was about 35 m/s. After that, velocity started to decrease and basically maintained in the scope of 5 m/s to 7 m/s. The reason for this phenomenon was as follows: With the increase of length in the cavity of air knife, backlash increased gradually and pressure loss also increased gradually. In addition, pressure provided at the inlet could not have an impact on the tail end of the cavity due to the long length of air knife. In this case, velocity peak was at the front end of the cavity and velocity at the tail end of the cavity decreased and maintained a certain scope.

Fig. 5Velocity distribution of outlet 1 and 3

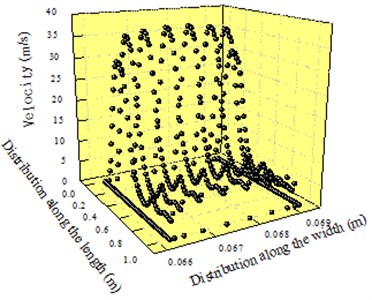
Velocity distribution of outlet 1 and 3

a) Three-dimensional distribution

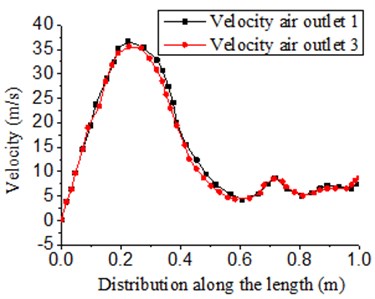
Velocity distribution of outlet 1 and 3

b) Two-dimensional distribution

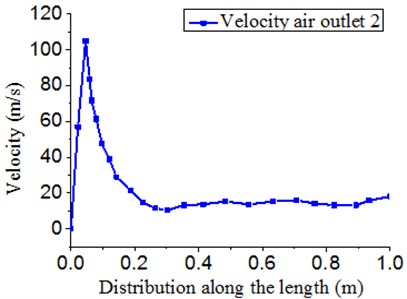
Fig. 6 presented the three-dimensional and two-dimensional distribution of velocity at outlet 2. Along the direction of length, velocity was high at the inlet and the peak velocity was 100 m/s. After that, velocity started to decrease and reduced to about 5 m/s at the position which was 210 mm away from the side of the inlet. Then, velocity fluctuated on a small scale around the value. The reason for this phenomenon was as follows: Outlet 2 was in the middle of cavity of air knife. There were not return air inlets on both sides. In this case, effective pressure difference was not generated at outlet 2, which led to the velocity flow of air. In addition, pressure provided by the inlet end could not have an impact on the tail end of outlet 2 due to the long length of air knife. Therefore, air entering from the inlet end flew out from outlet 2. In addition, velocity was high, but velocity at the tail end was low. The return air ratio of the original model was 0.33.

Fig. 6Velocity distribution of outlet 2

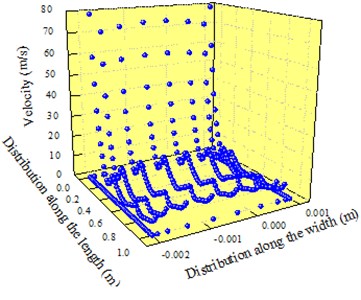
Velocity distribution of outlet 2

a) Three-dimensional distribution

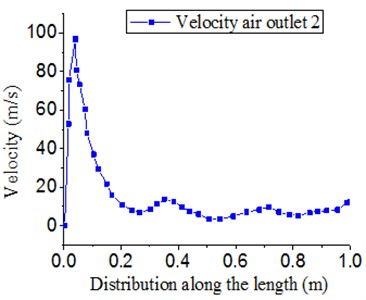
Velocity distribution of outlet 2

b) Two-dimensional distribution

5. Optimization design and analysis of air knife model

From the simulation result of the original air knife model, it could be seen that outlet velocity was not uniform. Wind velocity in high pressure area was obviously greater than that in other areas. The highest wind velocity was 35 m/s. The lowest wind velocity was 7 m/s. Wind velocity presented a large error. Therefore, the air knife model was far less than the design requirements of production and still remained to be further optimized.

5.1. Optimization proposal 1 of air knife

The result of the original model was analyzed. Optimization design module in ANSYS was used for optimization. Optimization process was shown in Fig. 1. The following changes were made to the optimized model: Guide plates were changed into rounded form from vertical plates. The number of guide plates decreased from two to one. The middle part of the guide plate was grooved. Specific size and form were shown in Fig. 7.

Fig. 7Geometric model and size of the optimized air knife model

Geometric model and size of the optimized air knife model

a) Three-dimensional model

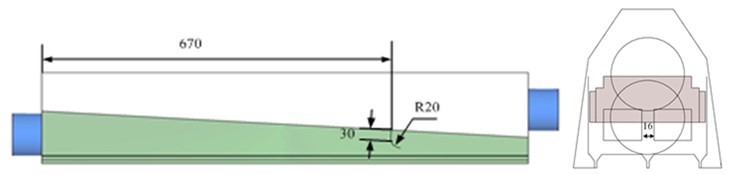
Geometric model and size of the optimized air knife model

b) The related size of the internal structure

The optimized structure used Fluent for solution. Boundary conditions were the same with those of the original air knife model. The three-dimensional trace and two-dimensional trace in the center symmetry plane were obtained, as shown in Fig. 8. Air entered from the air inlet. Due to the high pressure area at the inlet, a part of air flew out from the return air inlet and a part of air flew into the upper cavity from the gap between upper and lower cavities. Air continued to flow. Without the obstruction of the guide plate at the front end of the lower cavity, air flowed smoothly and airflow velocity was high in the second half of the cavity. After flowing through the guide plate, a part of air flew out from the return air inlet and a part of air flew into the upper cavity due to the guidance of the guide plate.

Fig. 9 presented the three-dimensional and two-dimensional distribution of velocity at outlet 1 and 3. As shown in the figure, the change trend of velocity was basically the same with that before optimization along the length of air knife. However, the peak velocity at the front end decreased to some degree. Velocity was 32.5 m/s. Velocity distribution at the tail end was uniform. In addition, velocity increased compared with that before optimization and reached about 15 m/s. Fig. 10 presented the three-dimensional and two-dimensional distribution diagrams of velocity at outlet 2. As shown in the figure, the distribution trend of velocity was the same with that before optimization, but velocity at the tail end was basically the same and maintained about 10 m/s. With a length of 1000 mm, the optimized air knife had return air ratio 0.33.

Through computation, it could be seen that return air ratios remained the same before and after optimization. From the perspective of velocity distribution at the return air inlet, however, velocity consistency of air knife at the return air inlet after optimization was obviously better than that of the original model before optimization.

Fig. 8The inner flow field of the optimized air knife model

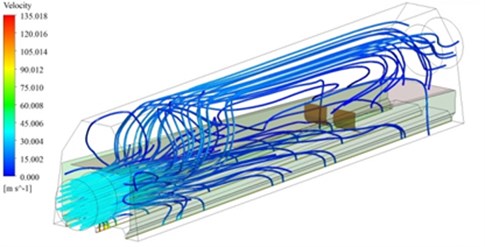
The inner flow field of the optimized air knife model

a) Three-dimensional trace

The inner flow field of the optimized air knife model

b) Two-dimensional trace

The inner flow field of the optimized air knife model

c) Contours of flow velocity

Fig. 9Velocity distribution of outlet 1 and 3

Velocity distribution of outlet 1 and 3

a) Three-dimensional distribution

Velocity distribution of outlet 1 and 3

b) Two-dimensional distribution

Fig. 10Velocity distribution of outlet 2

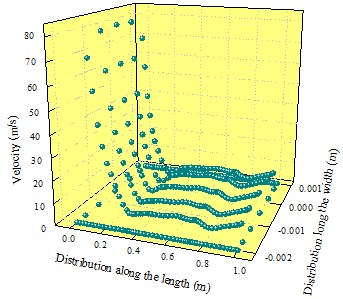
Velocity distribution of outlet 2

a) Three-dimensional distribution

Velocity distribution of outlet 2

b) Two-dimensional distribution

5.2. Optimization proposal 2 of air knife

To adapt to changes in the width of printing machine, the air knife was optimized based on proposal 1. The length of air knife was mainly improved. The improved air knife was about 1270 mm, as shown in Fig. 11. The velocity of the optimized structure was obtained, as shown in Fig. 12.

Fig. 11Improved model and three-dimensional trace of air knife

Improved model and three-dimensional trace of air knife

a) Improved geometric model

Improved model and three-dimensional trace of air knife

b) Three-dimensional trace

Fig. 12(a) presented the velocity distribution of outlet 1 and 3. Fig. 12(b) showed the velocity distribution of outlet 2. As shown in Fig. 11(b) and Fig. 12(a), the situation of velocity distribution was basically the same with that as the mentioned. Velocity peak was in the first half of the air knife and basically remained constant in the second half of the air knife. As shown in Fig. 12(b), it could also be seen that the velocity distribution of outlet 2 was basically the same with that of the mentioned model. However, pressure at the inlet could not form effective pressure difference at the second half of the outlet due to the increase of length of air knife. Therefore, velocity in the second half of outlet 2 was basically zero.

Fig. 12Velocity distribution of outlets

Velocity distribution of outlets

a) Velocity of outlet 1 and 3

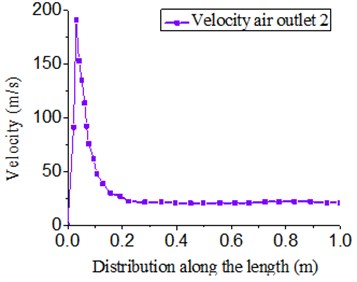
Velocity distribution of outlets

b) Velocity of outlet 2

Fig. 13Optimized model 2 of air knife

Optimized model 2 of air knife

Fig. 14Velocity distribution of outlet 1 and 3

Velocity distribution of outlet 1 and 3

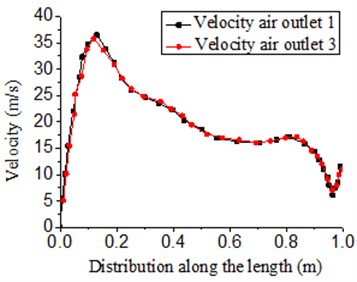
With the increase of length of air knife, the number of air knife outlets was modified, namely cancelling the original outlet 2 in the middle of air knife. Fig. 13 showed a proposal diagram for the model with a length of 1270 mm and 2 outlets and without guide plates in its cavity. Fig. 14 displayed the velocity distribution of outlet 1 and 3. The distribution form of velocity was basically the same with that as the mentioned. The peak velocity was 37.5 m/s. Velocity in the second half of the outlet started to decrease. However, the overall velocity in the second half of the outlet was high and basically maintained above 10 m/s.

5.3. Optimization proposal 3 of air knife

The optimization proposal 2 of air knife had already obvious consistency in velocity distribution at the return air inlet compared with its original model, but it failed to meet the requirements of engineering. Therefore, the optimization proposal 3 attempted to change the position of guide plates and conduct optimization and simulation for the model through software based on the proposal 2.

Through analyzing the result of model without guide plates in the above cavity and conducting simulation computation and analysis, the geometric model and specific size of the optimized model were obtained, as shown in Fig. 15.

The optimized structure was solved using Fluent software to obtain the three-dimensional trace and two-dimensional trace in the center symmetry plane, as shown in Fig. 16. Compared with Fig. 8, flow field in the first and second half of the cavity had an obvious improvement and was very smooth as the guide plate was in the middle half of cavity of air knife.

Fig. 15Geometric model and size of the optimized air knife model 3

Geometric model and size of the optimized air knife model 3

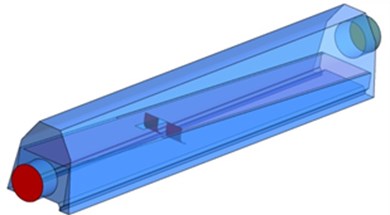
a) Optimized geometric model

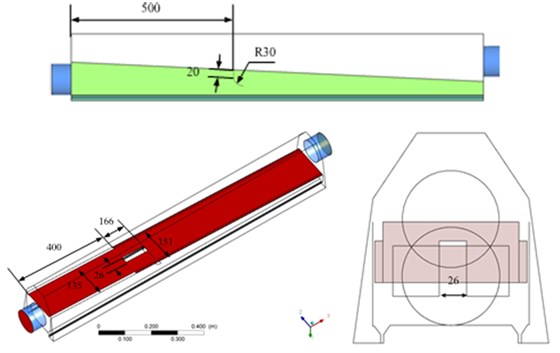
Geometric model and size of the optimized air knife model 3

b) The related size of the internal structure

Fig. 16The inner flow field of the optimized air knife model 3

The inner flow field of the optimized air knife model 3

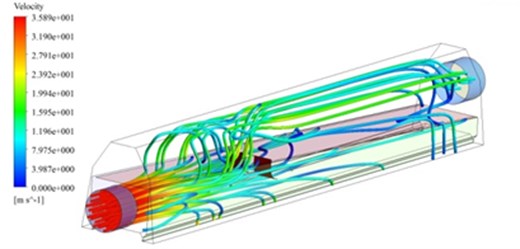
a) Three-dimensional trace

The inner flow field of the optimized air knife model 3

b) Two-dimensional trace

Fig. 17 presented the three-dimensional and two-dimensional distribution of velocity at outlet 1 and 3 of the new air knife structure which was 1270 mm. As shown in the figure, the distribution of velocity was basically the same with that in the cavity without guide plates. The peak velocity decreased slightly. Velocity was about 32.5 m/s. Velocity at the second half of the cavity basically remained the same. In addition, numerical value was relatively higher than that in Fig. 12. It was about 12 m/s. With a length of 1270 mm, the optimized new air knife structure had return air ratio 0.41.

Fig. 17Velocity distribution of outlet 1 and 3

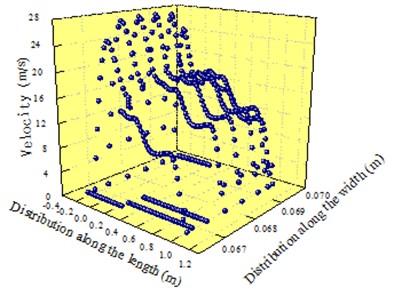
Velocity distribution of outlet 1 and 3

a) Three-dimensional distribution

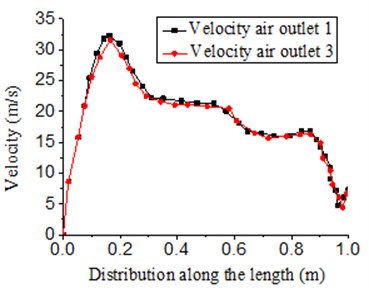
Velocity distribution of outlet 1 and 3

b) Two-dimensional distribution

Fig. 18Geometric model and three-dimensional traces of the improved air knife model 4

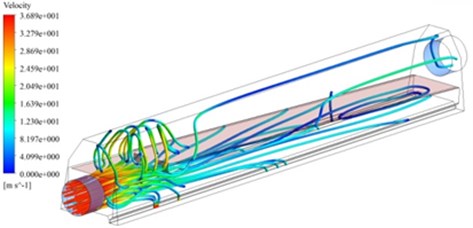
Geometric model and three-dimensional traces of the improved air knife model 4

a)

Geometric model and three-dimensional traces of the improved air knife model 4

b)

5.4. Optimization scheme 4 of air knife

To adapt to changes in the width of printing machine, the length of air knife was again improved. The improved air knife was about 1450 mm, as shown in Fig. 18. The optimized structure was solved using Fluent software to obtain the velocity distribution of air knife at the outlet, as shown in Fig. 19.

Fig. 18 presented the model with a length of 1450 mm and 2 outlets and without guide plates in the cavity and the distribution of three-dimensional traces. Fig. 19 showed the velocity distribution of outlet 1 and 3. The peak velocity was about 26.5 m/s. Velocity amplitude gradually decreased along the length of air knife.

Fig. 19Velocity distribution of outlet 1 and 3

Velocity distribution of outlet 1 and 3

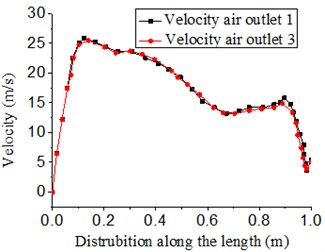
Fig. 20Geometric model and size of the optimized air knife model 4

Geometric model and size of the optimized air knife model 4

a) Optimized geometric model

Geometric model and size of the optimized air knife model 4

b) The related size of the internal structure

Fig. 21Velocity distribution of outlet 1 and 3

Velocity distribution of outlet 1 and 3

a)

Velocity distribution of outlet 1 and 3

b)

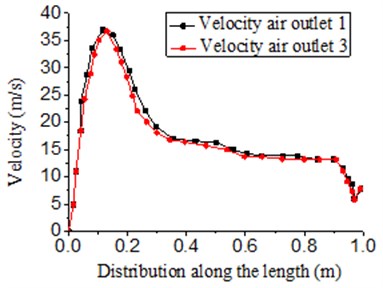
ANSYS design module was adopted to conduct simulation and optimization design for the optimized model of air knife without guide plates in proposal 4. Through conducting simulation computation and analysis many times, the proposal and specific size of optimized model were obtained, as shown in Fig. 20. Fig. 21 presented the three-dimensional and two-dimensional distribution of velocity at outlet 1 and 3 of the new air knife structure with a length of 1450 mm. As shown in the figure, the distribution of velocity was basically the same with that in the cavity without guide plates. The peak value increased slightly. It was about 37.5 m/s. Velocity at the second half of the cavity basically remained the same and the value maintained 15 m/s. The optimization proposal 4 had the return air ratio of air knife 0.41.

6. Conclusions

This paper conducted a parametric modeling for air knife structure in a printing factory, used HYPERMESH software to divide the meshes of air model and combined with actual conditions to define various boundary conditions in the inner flow field of air knife. In addition, this paper adopted fluid dynamics software Fluent to conduct numerical simulation for the internal airflow of air knife, obtained the distribution of flow field, conducted optimization design for the position of guide plates, the number of outlets and the size of return air inlet in the air knife based on the computational result, and obtained the following conclusions:

1) There were two guide plates and three outlets in the original air knife. Flow field was not uniform and velocity at outlets was low. With the increase of length of air knife, velocity of the middle outlet reduced to zero and showed no obvious effects. Therefore, three outlets of the original model were optimized into two outlets in the process of optimization.

2) Guide plates in the air knife had a great influence on the flow field in the air knife. Through optimization design, the inner flow field of air knife became uniform in the case of only one guide plate. When the guide plate was close to the front end of the air knife, the inner flow field of air knife was relatively uniform and velocity at outlets was relatively high.

3) Through ANSYS design module, this paper designed the model of air knives with different structures. Through repeated analysis, this paper determined proposal 4 as the optimal design proposal. At this time, the inner flow field of air knife was relatively uniform and velocity at outlets was high.

4) Four kinds of models of air knife were proposed and compared using the parameter analysis. Finally, an optimal structure was obtained in this paper. The design method in this paper could provide guidance for studying and designing air knife structures in the aspect of technological approach and theory.

References

  • Xiang W. J., Wu X. Q., Hou Z. H. Velocity calibration and investigation of flow field at air knife exit. Journal of Atmospheric and Environmental Optics, Vol. 8, Issue 5, 2013, p. 321-326, (in Chinese).
    Search CrossRef
  • Li Z. Y., Li J. S., Yin Y. B., Guo L. L. Casting equipment of stretch film production line and the air knife institution. Manufacturing Automation, Vol. 31, Issue 11, 2011, p. 104-106, (in Chinese).
    Search CrossRef
  • So H., Chung M. K. Numerical Verification of the performance of double jet air-knife system in avoiding the check-mark stain on the zinc coated surface. ISIJ international, Vol. 51, Issue 3, 2011, p. 521-522.
    Publisher
  • So H., Yoon H. G., Chung M. K. CFD analysis of sag line formation on the zinc-coated steel strip after the gas-jet wiping in the continuous hot-dip galvanizing process. ISIJ international, Vol. 51, Issue 1, 2011, p. 115-123.
    Publisher
  • Tamaddon A. H., Belmiloud N., Doumen G., et al. Evaluation of high-speed linear air-knife based wafer dryer. Solid State Phenomena. Trans Tech Publications, Vol. 195, 2013, p. 239-242.
    Publisher
  • Farkas J., Peter H., Christian P., et al. Characterization of the effluent from a nanosilver producing washing machine. Environment International, Vol. 37, Issue 6, 2011, p. 1057-1062.
    Publisher
  • Liu D., Sun Y. H. Gas flow dynamic study on air knife of vertical glass cleaner. Journal of North China University of Technology, Vol. 25, Issue 3, 2013, p. 50-55, (in Chinese).
    Search CrossRef
  • Olsson J., Ivarsson P., Winquist F. Determination of detergents in washing machine wastewater with a voltammetric electronic tongue. Talanta, Vol. 76, Issue 1, 2008, p. 91-95.
    Publisher
  • Persson T. Dishwasher and washing machine heated by a hot water circulation loop. Applied Thermal Engineering, Vol. 27, Issue 1, 2007, p. 120-128.
    Publisher
  • Lacanette D., Vincent S., Arquis E., et al. Numerical simulation of gas-jet wiping in steel strip galvanizing process. ISIJ International, Vol. 45, Issue 2, 2005, p. 214-220.
    Publisher
  • Gosset A., Buchlin J. M. Jet wiping in hot-dip galvanization. Journal of Fluids Engineering, Vol. 129, Issue 4, 2007, p. 129-466.
    Publisher
  • Ahn K. J., Chung M. K. A noble gas wiping system to prevent the edge overcoating in continuous hot-dip galvanizing. ISIJ International, Vol. 46, Issue 4, 2006, p. 573-578.
    Publisher
  • Choi J. H., Kim G. M. Development of an air-knife system for highly reproducible fabrication of polydimethylsiloxane microstencils. Journal of Micromechanics and Microengineering, Vol. 25, Issue 8, 2015, p. 2015-85014.
    Publisher
  • Albanesi A., Fachinotti V., Peralta I., Storti B. Application of the inverse finite element method design wind turbine blades. Composite Structures, Vol. 161, 2016, p. 160-172.
    Publisher
  • Wang L., Kolios A., Nishino T., Delafin P. L., Bird T. Structural optimisation of vertical-axis wind turbine composite blades based on finite element analysis and genetic algorithm. Composite Structures, Vol. 153, 2016, p. 123-138.
    Publisher
  • Lee H. W., Han J. Y., Kang J. H. A study on high speed coupling design for wind turbine using a finite element analysis. Journal of Mechanical Science and Technology, Vol. 30, Issue 8, 2016, p. 3713-3718.
    Publisher
  • Kwon S. B., Kwon Y. D., Lee S. J, et al. Numerical analysis for the coating thickness prediction in continuous hot-dip galvanizing. Journal of Mechanical Science and Technology, Vol. 23, Issue 12, 2009, p. 3471-3478.
    Publisher
  • Zhong H. F., Liu B. J., Zhang Q. F. The development of hot-dip galvanized strip technology abroad. Corrosion and Production, Vol. 23, Issue 11, 2002, p. 74-478.
    Search CrossRef
  • Safikhani H., Akhavan-Behabadi M. A., Shams M., et al. Numerical simulation of flow field in three types of standard cyclone separators. Advanced Powder Technology, Vol. 21, Issue 4, 2010, p. 435-442.
    Publisher
  • Qi H. Y., Qiao J. J., Wen D. Improvement of the air knife close-loop control system. Steel Rolling, Vol. 31, Issue 2, 2014, p. 65-66, (in Chinese).
    Search CrossRef
  • Yohannes G., Jussila M., Hartonen K., et al. Asymmetrical flow field-flow fractionation technique for separation and characterization of biopolymers and bioparticles. Journal of Chromatography A, Vol. 1218, Issue 27, 2011, p. 4104-4116.
    Publisher

Cited by

Air-knife design for improved drying efficiency in manufacturing flat-panel displays
Seungeun Park | Kang Park
(2022)
Experimental verification of the feasibility of the CFD approach in an air-knife
Ramazan Altay | Gulsen Yaman | Ramazan Yaman
(2022)
Investigation of Pressure Oscillation and Cavitation Characteristics for Submerged Self-Resonating Waterjet
Lihua Cui | Fei Ma | Tengfei Cai
(2021)

About this article

Received
11 February 2017
Accepted
18 June 2017
Published
31 December 2017
SUBJECTS
Flow induced structural vibrations
DOI
https://doi.org/10.21595/jve.2017.18242
Keywords
air knife
optimization design of structure
guide plate
flow field
Copyright © 2017 JVE International Ltd.
This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Creative Commons License