PI-tuned UPFC damping controllers design for multi-machine power system

1. Introduction

Power systems are under growing stress as deregulation presents a few new economic objectives for operation. Since control frameworks are being worked near their limits, shabby associations, unexpected occasions, sudden cause of failure in protection system, human blunders, and a large group of different elements may make the system to lose security and even cause system failure. Along these lines, the requirement for enhanced damping control method in a more extensive working is increasing more consideration. Among the accessible damping control techniques, each approach has favorable circumstances and hindrances in various frameworks. The viability of damping control relies upon the device picked, the system modular element, and the connected controller outline technique. The interconnected power systems may create electromechanical oscillations within the low frequency range of 0.2 Hz to 3.0 Hz.

A novel control of PV-STATCOM coordinated with power system stabilizers are used to damp out the electromechanical oscillations in a power system [1]. The author demonstrates that the coordinated control of the proposed method effectively enhances the damping oscillations which leads to improved power transfer in transmission lines. A unified model of a power system is employed with three FACTS devices (SVC, CSC, and PS) for suppressing oscillation and improving power system stability [2]. The author investigated the performance by analyzing the damping torque contribution to the power system framework. The UPFC is one of the most adaptable FACTS devices which can provide a sufficient control of real as well as reactive power flow and voltage regulation for the power system [3]. The author illustrated that the proposed UPFC power frequency model and UPFC network interface method improves the dynamic performance of the system and fairly control the damping oscillations.

Stability enhancement in multi-machine power system has been investigated for the best possible location of the UPFC based on small signal, voltage and transient stability using power system analysis toolbox (PSAT) software [4]. This small signal linearized model of UPFC is not suitable for damping controller design. Therefore, a linearized Phillips-Heffron model with STATCOM is proposed and demonstrates that the STATCOM stabilizer improves the power system oscillation stability [5]. An approach to the design of UPFC controllers has been presented and reveals that the damping is adversely affected by the incorporation of the DC voltage regulators [6]. Among the FACTS family, the UPFC is considered as the most powerful device which increase the power system stability [7]. The development of non-linear dynamic approximation using UPFC augmenting with non-linear adaptive control based on back-stepping for damping oscillation. A multi-machine system with long transmission line is compensated with UPFC-SMES. The author implemented DC-DC chopper to modulate the power of SMES to improve the transient stability [8].

The transient power system stability performance has been improved using the radial basis function neural network design for UPFC [9]. The author develops single neuron and multi neuron systems and implemented in the single machine infinite bus systems and three machine power system networks. The proposed RBFNN exhibits superior damping compared to the conventional PI controllers. A mixed sensitivity design of damping device with UPFC is presented [10]. The system implemented in the two areas four machine system gives satisfactory results both in frequency domain and through nonlinear simulations.

The problem of robustly UPFC based damping controller is formulated as an optimization problem considering the Phillips-Heffron model according to the eigen value-based multi-objective function comprising the damping factor, and the damping ratio of the undamped electromechanical modes to be solved using particle swarm optimization technique (PSO) that has a strong ability to find the most optimistic results [11]. A novel method for the design of output feedback controller for unified power flow controller (UPFC) is developed. The selection of output feedback gains for UPFC controllers is converted as an optimization problem with the time domain-based objective function which is solved by a particle swarm optimization technique (PSO) that has a strong ability to find the most optimistic results. Only local and available state variables are adopted as the input signals of each controller for the decentralized design [12]. Single objective optimization algorithms are not efficient in solving problems with more than one objective because optimizing one objective may lead to increase the conflicting objectives. Hence multi-objective optimization is proposed for tuning UPFC damping controllers installed in multi-machine system. The multi-objective algorithms such as NSGA-II and MNSGA-II are used for tuning the parameters of PI controller. Robust control methods are implemented to tune the PI controller-based UPFC for stability enhancement of a two-area four-machine and for SISO power system using evolutionary algorithms [13-20].

In this paper, a control mechanism of the PI tuned UPFC considering the two area multi-machine system using the NSGA-II and MNSGA-II algorithm to find the optimal values and to minimize the Integral Time Squared Error (ITSE) as the main objective functions. The rest of the paper is organized as follows. Section 2 briefly describes the UPFC multi-machine system. Section 3 narrates the nonlinear dynamic model of UPFC. Section 4 discusses about the implementation of the proposed NSGA-II algorithm and Section 5 presents the implementation of the MNSGA-II algorithm on the two area multi-machine system. Section 6 describes the problem formulation of proposed work. Section 7 the simulation results and discussion are presented. Section 8 concludes the paper.

2. UPFC with Multi-machine system

UPFC consists of two static converters basically series and shunt converter with a common DC link, coupling transformer connected to the AC system. The shunt converter operates as a static synchronous compensator (STATCOM) controls the AC voltage at its terminals and the voltage of the DC bus. It uses a dual voltage regulation loop: an inner current control loop and an outer loop regulating AC and DC voltages. Control of the series branch is different from the Static Synchronous Series Compensator (SSSC) where the two degrees of freedom of the series converter are used to control the DC voltage and the reactive power. In case of a UPFC the two degrees of freedom are used to control the active power and the reactive power [21]. The two-area four machine system used in this paper is an 12 Bus multimachine system as shown in Fig. 1. The system contains twelve buses and two areas, connected by a weak tie between bus 7 and 9. Totally two loads are applied to the system at bus 7 and 9. UPFC-based damping controller is connected between buses 7 and 10 with the main functions of power oscillation damping and power flow control carried out by four PI controllers.

Fig. 1Single line diagram of two area four machine system

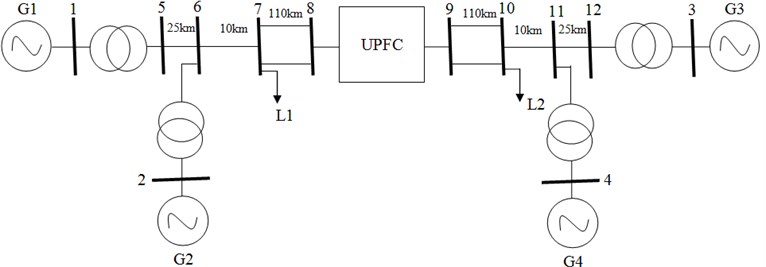
Fig. 2 depict the MATLAB simulation diagram of the proposed two area four machine system. The simulation test system consists of two areas linked by two 230 kV lines of 220 km length. Two identical generators in each area of 13.8 kV/1000 MVA is connected in the network. This system is used in this work to study about the low frequency oscillations of power system. UPFC-based damping controllers designed for two-area-four machine is also shown in Fig. 3.

Fig. 2Simulation diagram of the proposed system

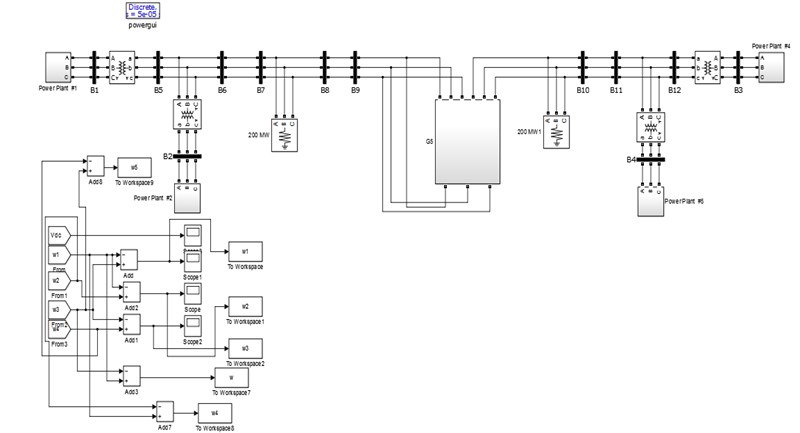
3. Nonlinear dynamic model of the UPFC

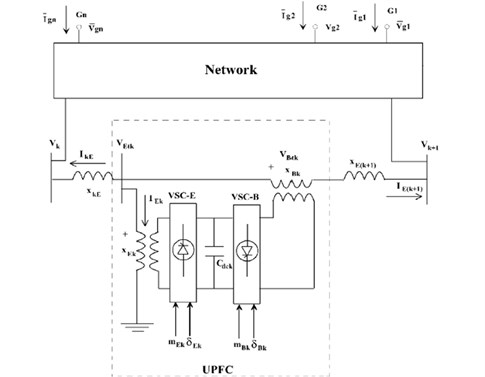
To enhance the small signal stability of the system, a dynamic model of the UPFC is very much essential in the power system network. The modeling of UPFC can be done using park’s transformation neglecting resistance of UPFC transformers. The complete multi-machine system with the UPFC located near the load side is discussed in Section 2. The single line diagram of $n$-machine UPFC power system is shown in Fig. 4. The four control parameters of UPFC are $m_B$ – reactive power regulator, ${\delta }_B$ – active power regulator, $m_E$ – AC voltage regulator, ${\delta }_E$ – DC voltage regulator.

Fig. 3Simulink diagram of UPFC damping controller

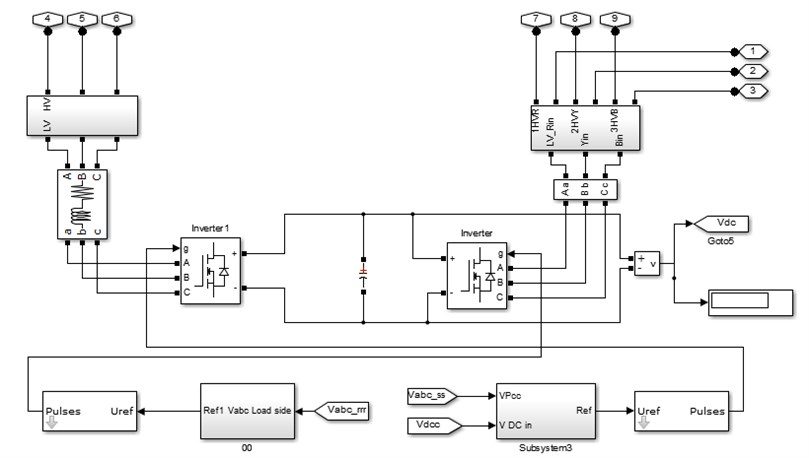
These control inputs provide power compensation in series and shunt line [15].

The $d$-$q$ transformation of excitation and boost systems denoted as $E$ and $B$ in Eqs. (1-3) respectively are:

where $C_{dc}$ – DC link capacitance, $V_{dc}$ – DC link voltage.

The non-linear equations Eqs. (4-9) of the power system under consideration are:

where $i_t$– armature current, $v_b$ – bus voltage, $v_{Et}$, $v_{Bt}$, $i_B$ and $i_E$ are the excitation transformer voltage, boosting transformer voltage, boosting transformer current and excitation transformer current respectively.

The state space matrix of the variables under consideration is represented in Eq. (10):

Fig. 4Single line diagram of n-machine UPFC system

4. Implementation of Nondominated Sorting Genetic Algorithm II (NSGA-II)

NSGA-II is a multi-objective optimization problem working on Pareto-optimal solutions. It uses non-dominated sorting, particles which are not dominated by other particles are assigned as $F_1$ (front 1), and particles which are dominated by other particles in $F_1$ are assigned as $F_2$ (front 2) [16, 17]. The selection is made based on the tournament i.e. the particles with lowest crowding distance are selected if the two particles are from the same front. $O\left(MN\right)$ comparisons are required for finding the first non-dominated solution front. $O\left(M{N}^2\right)$ comparisons are required for finding the second non-dominated solution front where $M$ is the number of objectives, and $N$ is the population size.

5. Implementation of Modified Nondominated Sorting Genetic Algorithm II (MNSGA-II)

NSGA-II algorithm is a good optimization technique for multi-objective problems. However, the problem with NSGA-II is maintaining the diversity and uniformity. Hence in NSGA-II, Dynamic Crowding Distance (DCD) is incorporated to enhance the diversity and uniformity to refine solutions further called as Modified Nondominated Sorting Genetic Algorithm II [18, 19].

6. Problem formation

NSGA-II and MNSGA-II algorithms are implemented to tune the PI controller-based UPFC for stability enhancement of a two-area four-machine power system. Tuning of PI controllers is done by optimizing the error signal and control input values, formulated as multi-objective optimization problem. Integral Time Squared Error (ITSE) is the performance measure taken in this work. The objective functions are formulated as given in Eqs. (14-16) to reduce the peak overshoot and the settling time:

where:

where $e$ is the error signal i.e, speed deviation of four generators for local and inter-area modes and $u$ is the input control signal, $t$ is the time of simulation.

The parameters of the system with the proposed MNSGA-II-based UPFC controller shifts to the left by a significant value in the s-plane indicating that the proposed UPFC controller provides better dynamic stability to the power system. The negative real and complex eigen values confirm that the system is in fast decaying damped oscillatory mode. The eigen value analysis shown in Table 2 reveals that the proposed controller enhances the dynamic stability of the power system greatly. The system eigen values are in the left half of the s-plane which assures the stability of the system.

NSGA suffers from computational complexity, non-elitist approach and the need to specify a sharing parameter. An improved version of NSGA known as NSGA-II. The crowding distance operator will ensure diversity along the non-dominated front, lateral diversity will be lost. NSGA-II is a fast and elitist MOEA and implements elitism for multi-objective search, using an elitism preserving approach. Diversity and spread of solutions are guaranteed without the use of sharing parameters. When two solutions belong to the same Pareto-optimal front, the one located in a lesser crowded region of the front is preferred. However, the lacking of NSGA-II in lateral diversity is one of the major shortcomings which guides towards false Pareto-front. The important properties involved in MNSGA II algorithm are controlled elitism and Dynamic Crowding Distance. Controlled elitism prevents the number of individuals in the current best non-dominated front. It maintains number of individuals in each front distributed predefined manner. Dynamic crowding distance is mainly used to maintain horizontal diversity and, it removes one individual with smaller DCD value at every time and recalculates DCD for the remaining individuals.

7. Results and discussion

Both the NSGA-II and MNGA-II algorithms were implemented in the power system network discussed in Section 4 and 5 and the simulation results obtained are presented and discussed in this section. In this work, both the local area and inter-area oscillation modes have been considered to calculate the Integral Time Squared Error (ITSE) based on the values of the PI controller tuning parameter $K_p$ and $K_i$. The selection of the Pareto-front for both the algorithms is shown in Fig. 5.

Fig. 5a) Pareto-front for NSGA-II, b) Pareto-front for MNSGA-II

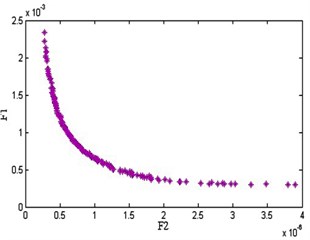
a)

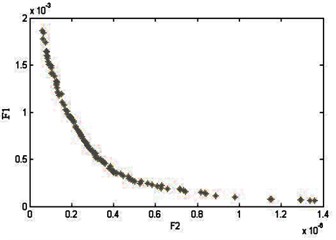
b)

Initially the local area mode oscillations between two different generators have been studied and the results have been analyzed for damping of oscillations. It was inferred from the results shown in Fig. 6, the MNSGA-II algorithm yields better results in damping oscillations quickly compared with the other two algorithms.

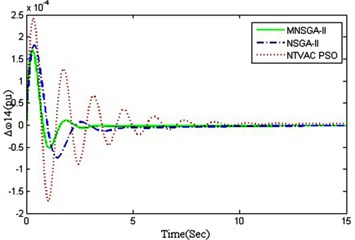
From the results yielded for the local area mode oscillation, the implementation of algorithm has been studied for the inter area mode oscillations between the generators and the results obtained has been shown in Fig. 7. It clearly depicts that once again the MNSGA-II tuned UPFC controller produces very lesser time to settle and quickly damps out the inter-area mode oscillations between generators which improves the stability of the power systems.

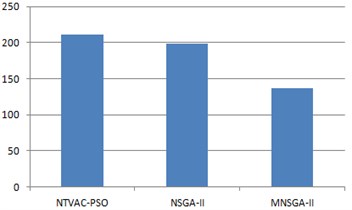
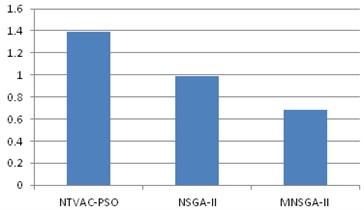
The gain values of $K_p$, $K_i$ of the four PI controllers with ITSE and ISE are tabulated in Table 3 and Table 4. It reveals that the MNSGA-II based PI tuned controller gives lesser ITSE compared to other algorithms with improved damping performance with minimum overshoot and undershoots. Fig. 8(a) shows the ITSE convergence for MNSGA-II, Fig. 8(b) shows the comparison results of ITSE and Fig. 8(c) shows the comparison results of ISE.

Fig. 6Local area mode oscillations between generator 1 and 2

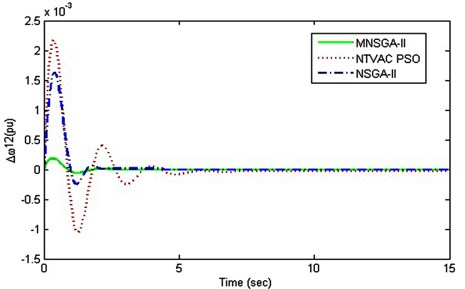
Fig. 7Inter area mode oscillations

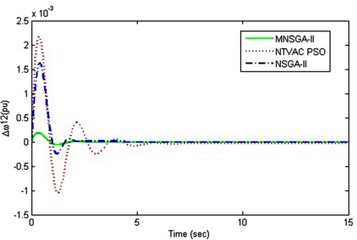
a) Between generator 1 and 3

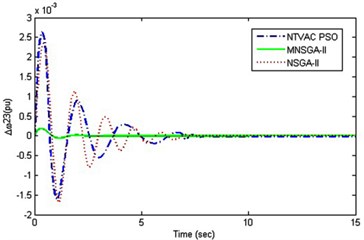
b) Between generator 2 and 3

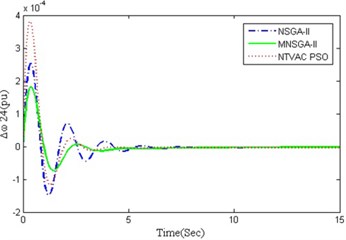
c) Between generator 2 and 4

d) Between generator 1 and 4

The control energy results obtained for the four PI tuned controllers are shown in Fig. 9(a) to 9(d) where the control energy is the input error functions of the controller. From the results, it is inferred that MNSGA-II-based PI tuned controllers damp out the oscillations by controlling the control energy with less overshoot and minimum settling time compared to NSGA-II based PI tuned controller.

Fig. 8a) ITSE convergence for MNSGA-II, b) ITSE convergence comparison results, c) ISE convergence comparison results

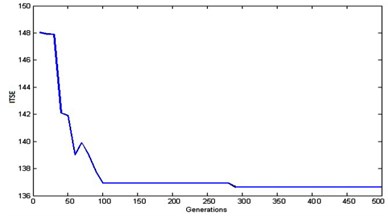
a)

b)

c)

Fig. 9Control energy

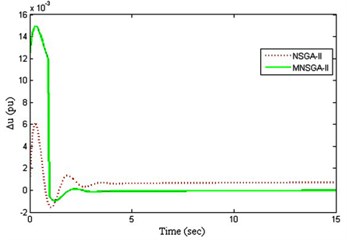
a) PI Controller 1

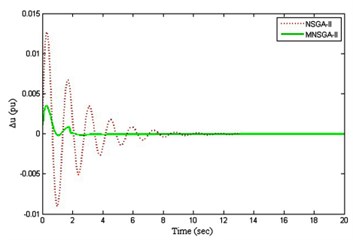
b) PI Controller 2

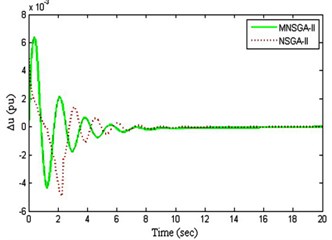
c) PI Controller 3

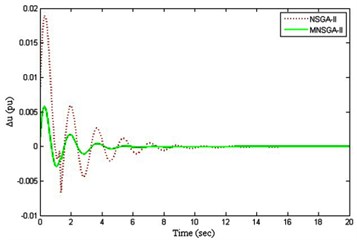
d) PI Controller 4

8. Conclusions

In this work, coordinated designs of the NSGA-II and MNSGA-II-based PI-tuned UPFC controllers have been carried out in two areas four machine systems to enhance damping of oscillations. The results obtained and presented establish that the designed PI-tuned UPFC damping controllers are more competent to increase the damping coefficient and damping ratio of the electromechanical modes. The results of time domain simulations on the multi-machine system have revealed that MNSGA-II-based PI-tuned UPFC controllers damped out oscillations quickly and enhance power system dynamic stability with minimum undershoot and overshoot compared to NSGA-II. Apart from the above, the eigen values were obtained and proves that the stability of the system gets improved. Also, the ISE parameter has also been considered for stability analysis and the comparison characteristics chart has been depicted. The proposed method also provides enhanced performance compared to NTVAC-PSO-tuned UPFC damping controller.