Active control of the nonlinear bending behavior of magnetorheological elastomer sandwich beam with magnetic field

1. Introduction

Today, it is possible to go further with the magnetorheological materials: controlled by magnetic field, they can change continuously, quickly and reversibly some of their characteristics and adapt to a new environment; the interest of the industry is related to many possible applications, including active damping devices [1]. Zhou and Wang [1, 2] formulated an analytical model of the vibrating motion of a sandwich beam under a uniform magnetic field, perpendicular to the direction of the thickness. To validate the analytical model, they conducted a second study based on numerical modeling to control the rheological properties. Dwivedy et al. [3] studied the parametric instability areas of a sandwich beam with a magnetorheological elastomer core identical to that studied by Zhou and Wang [1, 2], but subjected to a periodic load, to determine the adjustment advantages of the mechanical properties of the loaded elastomers exposed to a magnetic field. They used Hsu’s method to determine the zones of instabilities associated with single and combined resonance frequencies for different boundary conditions [3]. Nayak et al. [4] studied the vibration reduction of a sandwich beam with three cores, an uncharged elastomer core, a charged elastomer core with ferromagnetic particles, and a charged core with carbon particles. Areas of parametric instability for the two different types of particle charging were studied only for the first three vibration modes to illustrate the passive and active vibration reduction. Sun et al. [5] investigated the controllable capability of an adaptive MRE sandwich beam; the experimental investigations showed that the MRE damps unwanted motion. Hu et al. [6, 7] conducted an experimental study on the dynamic response of a sandwich beam containing two aluminum layers with an MRE core under non-homogeneous magnetic fields; it was shown that a reduction of 13.9 % is achieved on the first mode of transverse motion. More recently, the semi-active control of an MRE sandwich beam was investigated under different loadings [8]; the results showed that the changing stiffness and damping of the MRE layer controls the motion amplitude.

Based on the above works, the static study and characteristics of bending sandwich beam were investigated in this present paper. By this way, we can evaluate the influence of the magnetic field and the length of the adaptive beam on the amplitude of transverse displacement [9], we have therefore developed an adaptive structure to dampen the amplitude of the displacements in the form of high energy dissipation.

2. Analytical modeling of bending behavior

The studied structure is a sandwich beam simply supported with a core made of magnetorheological elastomer (MRE) and two skins made of aluminum such as shown in Fig. 1 [10]. Aluminum skins and MRE, Fig. 2, have different static bending behavior.

Fig. 1Sandwich beam in composite material (MRE)

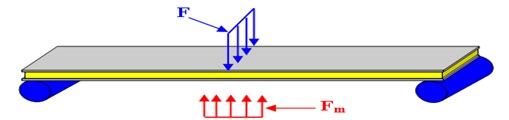
Fig. 2Geometrical architecture of the sandwich beam

In order to best represent the static behavior of the beam without resorting to complex theories of higher order, the Nilsson model [7], taking some of the principles from the Timoshenko theory [11] will be used. However, Nilsson works were interested in a sandwich structure where skins are homogeneous materials.

In this case, the equilibrium equation, written as a function of the longitudinal elasticity and the shear moduli of the beam, is given by [12]:

The integration of Eq. (1) makes it possible to write the expression of the bending:

Bending therefore depends on the equivalent rigidity of the beam in bending ${\left(EI\right)}_{eq}$ and in shear ${\left(GA\right)}_{eq}$.

The bending in the center of the beam can be written as:

with:

where: $h_b=h_t=h$ et $E_b=E_t=E_p$.

And its equivalent shear stiffness ${\left(GA\right)}_{eq}$ is expressed as:

3. Finite element modeling

The calculation of structures by finite elements is performed using the Abaqus software. The element used is a 2-D element, CPS4 type with four nodes (Fig. 3(a)). The sandwich material is modeled by three structures, two isotropic elastic structures corresponding to the aluminum skins, and an MRE core. The skins are characterized by the Young’s modulus, Poisson’s ratio and density, given in Table 1. The mechanical and rheological characteristics of the MRE measured experimentally were given by [13]. The sandwich beam model realized in Abaqus is given in Fig. 3(b, c).

Fig. 3Sandwich beam model in Abaqus: a) mesh element in Abaqus: 2D type CPS4, b) beam without meshing, c) beam with meshing

a)

b)

c)

Fig. 4Deflection of the beam for different values of the magnetic field intensity

a)$B=0T$

b)$B=0.1T$

c)$B=0.3T$

d)$B=0.5T$

Fig. 4 shows the deflection of the composite material structure for different values of the magnetic field. It is observed that the deflection decreases with the increase of the magnetic field intensity, this is due to the increase in the rigidity of the magnetorheological elastomer.

4. Experimental analysis

4.1. Description of the test

Sandwich specimens of size 200 mm×35 mm×4 mm are manufactured using two aluminum skins of 1 mm thickness and an elastomer core charged at 30 % by ferromagnetic particles of micrometric size, which is inserted between the two skins (Fig. 5). The three-point bending test is carried out using a Zwick 2.5 kN machine (Fig. 6). The tests are carried out with a constant deformation rate of 1 mm/min in order to be able to consider that the loading is quasi-static. The applied force and the displacements are measured by the cell of the machine.

Fig. 5MRE sandwich specimens

Fig. 6Three-point bending test machine

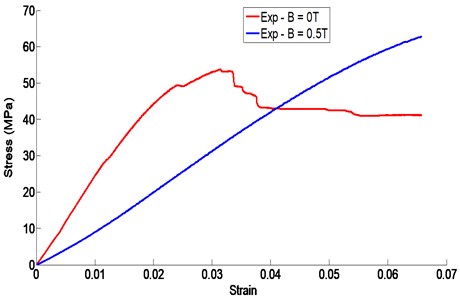
4.3. Interpretation of the results (stress/strain)

It can be seen from the curves of Fig. 8 that the specimens exhibit a non-linear behavior even at small deformations; it is possible to define distinct domains:

For the test piece subjected to an intensity of 0$T$, we can observe that the behavior is more linear at the beginning of the stress value less than 10 MPa, then a non-linear behavior until the rupture. On the other hand, the specimen subjected to an intensity of 0.5$T$ presents a non-linear behavior even with practically negligible strains.

Fig. 7Three-point bending strength-displacement curve of the sandwich beam with and without magnetic field intensity

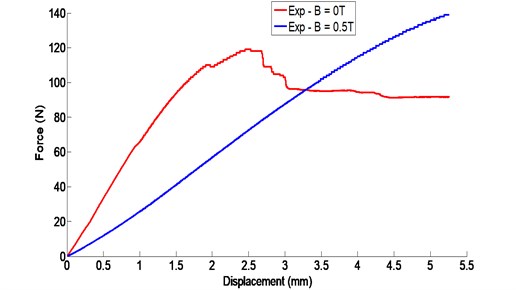
Fig. 8Three-point bending stress/strain curve of the sandwich beam with and without magnetic field intensity

5. Conclusions

The magnetic properties of MRE have been studied by several researches before, but the study on sandwich structures in MRE is new. The MRE manufactured with iron particles dispersed in natural rubber was studied applying magnetic fields varying from 0 to 0.65$T$. The results obtained by the analytical study (Section 2) are compared with those obtained by finite element analysis. The determination of the deflection was performed taking into account the variation of the rheological characteristics of the MRE according to different magnetic field intensities.

The analysis of the results shows that:

1) Overall, the deflection of the beam decreases with the increase of the magnetic field intensity;

2) The results obtained by finite elements and those obtained by analytical study are in good agreement for all magnetic field intensities;

3) The deflection obtained numerically deviates slightly with the increase of the magnetic field intensity of: 6.25 % for $B=0.1T$, 7 % for $B=0.1T$, 9 % for $B=0.5T$, and 12.25 % for $B=0.65T$;

4) The evolutions of the deflection as a function of the length of the beam depend on several parameters: the distribution of strain energy between the skins and the core, the magnetic field intensity as well as the elastomer charging rate by the iron particles;

5) The magnetic field intensity has a significant influence on the rigidity of the magnetorheological elastomer;

6) A difference between the analytical values of deflection of the beam and those obtained by finite elements analysis appears for high values of the magnetic field intensity. This gap could be explained by the influence of the secondary effects of the magnetic field on certain parameters which are not taken into account by the theoretical study.