The definition of productive reservoirs by the method of fuzzy inference

1. Introduction

The lithological classification and allocation of reservoirs are based on the difference of physical and geophysical parameters of rocks. Finding the values of physical and geophysical parameters in some ranges makes it possible to predict the lithology of the formation. Since the ranges overlap for different rocks, it is necessary to identify the lithology of rocks by a set of reservoir, physical and geophysical parameters.

In automated systems, interpretation of geophysical research wells used algorithm lithological division with a scan to dam [1, 2]. The algorithm consists in compiling a complex code according to the data of geophysical surveys of wells and comparing it with predictive diagnostic codes representing the geophysical characteristics of rocks in the section. Approximate interval estimates are used instead of numerical values. For example, small values are assigned the code 00, medium – 01, large – 10, very large – 11. The set of different geophysical measuring methods, recorded in the accepted order, forms a complex code of lithological type. The comparison of the complex formation code with the diagnostic one makes it possible to determine the type of lithological rock in this formation. We note two main drawbacks of this method. The first is that in case of mismatch of the actual code with any diagnostic, lithological type of formation remains uncertain. The second disadvantage is the need to evaluate the boundary values of the geophysical methods in the preparation of complex codes. From the method of division of changing parameters on the intervals strongly depends on the form of a comprehensive code.

The further development of this method is the algorithm of lithological dissection of the section with probability estimation [8]. For this formation, the most probable lithological type to which it should be assigned is determined by the complex of indications of geophysical methods [1]. This algorithm eliminates the first drawback of the method of lithological dismemberment by diagnostic codes, but is not exempt from the need to specify intervals. In addition, the assumption is made about the normal distribution of the indications of the methods of geophysical studies of wells.

These algorithms are not representatives of intelligent systems, as they are not self-adjusting and self-learning. Class of information systems based on fuzzy logic [9] provides a more effective use of existing knowledge about a certain object. This allows to apply fuzzy logic in intelligent systems of interpretation of well geophysical research materials.

The advantages of fuzzy expert systems are: the possibility of parallel implementation of the existing rules and forecasting new States of the system; the plurality of interpretations of the values of variables, as well as the fact that the description of the problem and the rules is conducted in natural language using linguistic variables [6].

2. The model of the system

The method of fuzzy inference is based on the introduction of some rules-statements that make the result dependent on the conditions [3, 10]. Conditions and results are described by linguistic variables. In the same way as in the algorithm lithological division at the diagnostic codes, for the variables of the system (indications of geophysical methods) is selected resolution form and entered the encoding of the values of linguistic variables in the form of numbers of terms of the set. As a variable, depending on the indications of geophysical methods, the lithological type acts. The rules necessary for fuzzy selection can be formulated using the table of diagnostic complex codes [1]. For example, the complex codes for the terrigenous section given in [1] are replaced by the rules in Table 1.

To rules (Table 1) it is necessary to add additional rules received on the basis of the decoded data on interpretation of materials of geophysical researches of wells (GRW).

3. Description of the algorithm

Let’s consider the algorithm of recognition of lithology of layers on the basis of fuzzy logic with the use of the known base of rules that provides more effective use of the available knowledge about some object.

The preliminary stage for this algorithm is the procedure of splitting the well into layers, which determines the composition of the layers on the basis of preliminary data on the characteristics of the wells of this field.

In the layers, which can be obtained by means of neural network separation [7, 11], are the average values of the parameters: $\mathbf{p}\left(h\right)=\underset{h_{BL}\left(h\right)}{\overset{h_{BR}\left(h\right)}{\int }}\mathbf{P}\left(\xi \right)d\xi /h_{BR}\left(h\right)-h_{BL}\left(h\right)$, where $h$ – depth; $h_{BL}\left(h\right)$, $h_{BR}\left(h\right)$ – left and right boundaries of the formation, lying at a depth of $h$, respectively; $\mathbf{P}\left(h\right)$ – the values of the parameters measured by any method.

In order to train the system for the subsequent forecasting of reservoir productivity, it is necessary to involve the results of processing and interpretation of several wells. For training and forecasting, consider the fuzzy inference method. We consider a system corresponding to a certain set of selected layers $G$. the Properties characterizing this class of layers are denoted by $v_i$, $i=\overline{1,m}$. the properties become variables of the system under consideration, which is a model of the class $G$. one of the properties is the lithological type. Other properties are the average integral values of the parameters $p\left(h\right)$. The selected properties are characterized by a set of linguistic variables $x_i$, $i=\overline{1,m}$. Linguistic variables can have the main values: “low” (L), “medium” (M), “high” (H), and, if necessary, some intermediate {L, LM, M, MN, H}. We write $n$ rules linking the state variables of the system, in the form of:

where $Z_{ij}$ is some value from the term set {L, LM, M, MN, H}.

The rule is read: variable $x_k$ takes the corresponding value from the set $\left\{L,...,H\right\}$, if other variables $x_i$, $i=1,...,m$, $i\ne k$ have some values from this set.

Rules (1) may be established by experts. If there is a data system corresponding to the objects $G$, the rules can be obtained by the classification learning algorithm.

We introduce the encoding of the values of linguistic variables in the form of the numbers of terms of the set $x_i=k$, $k=\overline{0,K_i}$, $i=\overline{1,m}$. Each term is characterized by its membership function ${\mu }_{ik}\left(v_i\right)$. Let the objects $g_j\in G$, $j=\overline{1,n}$ correspond to the data system. The values of the system variables $x_i$, $i=\overline{1,m}$ form the object-property matrix $Q=‖q_{ij}‖$, $i=\overline{1,m}$, $j=\overline{1,n}$. The columns of the matrix $Q$ is formed by the values of the variables $x_i=k$, $k=\overline{0,K_i}$, $i=\overline{1,m}$. Thus, the elements of the matrix $Q$ are the values of $Z_{ij}$ from Eq. (1). For certainty, we believe that the lithological type corresponds to the first variable $v_1$. States $c\in C$ correspond to combinations of values of variables $v_i$, $i=\overline{1,m}$. Each state will be considered as a rule. If the sample is small, the expert can add a number of additional rules to the obtained rules, obtained on the basis of decoded data on the interpretation of GRW materials.

To apply the technique of fuzzy logic required is the assignment of membership functions for each term. If a data system is available, the optimal parameters of the fuzzy system can be obtained as a result of training. You can use a point estimation algorithm to do this. There is a data system in which the training sample is allocated. After selecting the resolution form, the rules are determined (1). Then, the intersection of fuzzy sets operation calculates the degree of execution of each rule. For the right part of the $j$-th rule is the degree of ownership ${\mu }_j\left(Y\right)=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\left[{\mu }_i\left(X_i\right)\right]$, where $X_i$ – the base variable for the linguistic variable $Y$, included in the left part of the rule ($i=1,...,m$, $i\ne k$), and $X_i$ – the base variable for the linguistic variable $x_k$, included in the right part of the rule. The membership function corresponding to the variable $Y$ is determined by the ratio:

where ${\mu }_k\left(Y\right)=b_k^{L_k}\left(Y\right)\text{,}$$b_k^l\left(Y\right)=b_k^{l-1}\left(Y\right)+{\mu }_k^l\left(Y\right)-b_k^{l-1}{\mu }_k^l\left(Y\right)\text{,}$$l=\overline{1,L_k}\text{;}$$b_k^0=0$ using a probabilistic $Y$-conorm, where $L_k$ is the number of rules with the same right part.

The function Eq. (2) calculates the point estimate of the variable $Y$:

The functions of the trapezoidal membership can be described using the coordinates of the corner points of the trapezoids for each term. We denote these parameters $x_{pi}^t$, $i=\overline{1,m}$, $t=\overline{1,T_i}$, $p=\overline{\mathrm{1,4}}$, where $T_i$ is the number of terms for the variable $x_i$. the form of the rule also determines the left and right boundaries of terms $B{L}_i^t$, $B{R}_i^t$, $i=\overline{1,m}$, $t=\overline{1,T_i}$, which generally do not coincide with $x_{1i}^t$, $x_{4i}^t$.

The result of the point estimation algorithm is the result $Y_0$, depending on the rules (1) and parameters $x_{pi}^t$, $B{L}_i^t$, $B{R}_i^t$, $i=\overline{1,m}$, $t=\overline{1,T_i}$, $p=\overline{\mathrm{1,4}}$. Therefore, we can assume that the function is defined: $Y=F(\mathbf{X},\mathbf{Z})$, where $\mathbf{X}=\left[X_i\right]$ is the vector of input variables; $\mathbf{Z}$ is a vector consisting of variables (parameters) $x_{pi}^t$, $B{L}_i^t$, $B{R}_i^t$, $i=\overline{1,m}$, $t=\overline{1,T_i}$, $p=\overline{\mathrm{1,4}}$.

For training, we define the target function:

where $\left\{⟨{\mathbf{X}}^s,Y^s⟩\right\}$, $\left(s=\overline{1,h}\right)$ is the data system used for training (training sample); $h$ is the amount of training sample.

4. Results and discussions

The minimization of the objective function Eq. (3) gives the optimal values of the parameters of the fuzzy system $Z=\{x_{pi}^t,B{L}_i^t,B{R}_i^t,i=\overline{1,m};t=\overline{1,T_i};p=\overline{\mathrm{1,4}}\}$. the Effective solution of the problem (4) is again carried out using a hybrid genetic algorithm BGAVM. The optimal membership functions obtained as a result of training on the rules (1) and corresponding to the considered geophysical methods are used further for the prediction and identification of lithological types of formations in new wells.

Fig. 1The results of forecasting of productivity of the formation

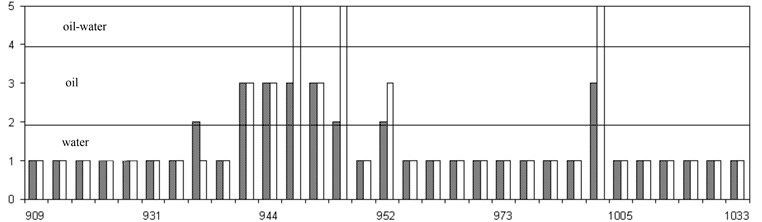
a)

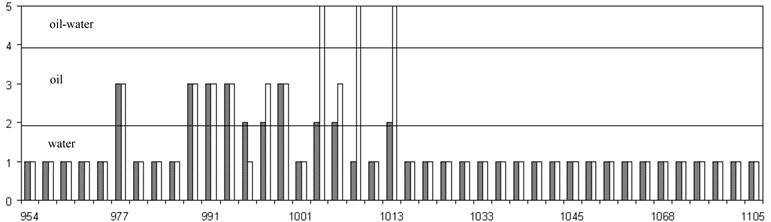
b)

In Fig. 1, a and b for two wells shows the forecast of reservoir productivity in comparison with the data decoding. The forecast corresponds to the dark bars, decoding – light. It is seen that for both wells, the productive formations corresponding to oil are recognized by 100 %. Water layers are recognized at 95 and 97 %, respectively. Layers of type oil-water are recognized worse: the system took 5 layers of oil-water to oil and 1 layer to the water.

5. Conclusions

A method has been developed to determine the informativeness of logging methods when recognizing the lithologic structure of a borehole section by the NL model, depending on the number of logging methods. It is important that the trained fuzzy system does not pass the productive formations of the oil type, and therefore the method can be used for rapid analysis of new wells.