A single neuron PID control method based on Smith predictor for active balancing control of rotor with time-delay

1. Introduction

The balancing control problem is a key problem that affects the stability of rotating machinery [1]. Active balancing control can realize unbalance correction with the machine running, which is an advanced technology to solve the dynamic balancing problem. In the process of rotor active balancing, there is an inevitable time-delay, which can cause instability of control system [2].

Currently, active balancing control with time-delay has attracted the widespread attention of many scholars. M. R. Ghazavi and Q. Sun analyzed the nonlinear dynamics behaviors of a rigid rotor supported by magnetic bearings, and they designed a nonlinear PD controller by adopting a time varying stiffness term [3]. However, the control law is only applicable to rigid rotor rather than to flexible rotor. Ren et al. analyzed the effects of time-delay on the stability of the rotation modes for the magnetically suspended flywheel (MSFW) with strong gyroscopic effects, and they presented an effective phase compensation method based on cross-channel [4]. However, this idea only applies the method of solving nonlinear dynamic systems without time-delay to time-delay systems; this method requires that the time-delay system is a weak linear system. Li et al. designed a simple proportional differential (PD) controller and acceleration feed-forward with an output predictor. They also produced the control law for each vibration mode in order to improve the performance of the control system [5]. The control method is mainly used in active vibration control of structures.

In a word, active balancing control of rotor is generally applied to rigid rotor with small time-delay currently. Therefore, in the current work we aimed to propose a new method to overcome the influence of time-delay on system. The main objectives of this study were four folds: (1) establish the dynamic model of flexible rotor by simplification and abstraction of high speed rotor; (2) build the Smith predictor of flexible rotor with time-delay to eliminate the influence of time-delay factor in the system; (3) design a single neuron PID control method based on Smith predictor to adjust the parameters of the PID controller adaptively; (4) validate the proposed method by the simulation.

2. Dynamic model of rotor system with time-delay

High speed rotor usually produces deformation during operation. Therefore, the model of flexible rotor is established as shown in Fig. 1. The bending stiffness of the axis at the midpoint is $k$, the mass of the disk is $m$ and the damping coefficient is $c$. It is assumed that $S$ is the geometric center of the disk, the flexible axis passes through the geometric center of the disk $S$, and the centroid of the disk is $G$. Because of the uneven material and manufacturing error, there is a deviation between centroid $G$ and geometric center $S$, and the eccentricity is $SG=e$. When the disk is stationary, the flexible shaft is located at the $z$ axis (AB line). When the disk rotates at angular speed $\omega$, the rotor produces deflection under the action of unbalanced inertia force, and the flexible shaft presents a bow shape. The flexible shaft rotates around the $z$ axis. It is assumed that the intersection point between the axis $AB$ and the center of the disk is $O$.The $AB$ line is taken as the $z$ axis, the initial position of $SG$ is taken as $x$ axis, and $y$ axis is perpendicular to $x$ axis and $z$ axis.

Fig. 1Schematic diagram of flexible rotor structure

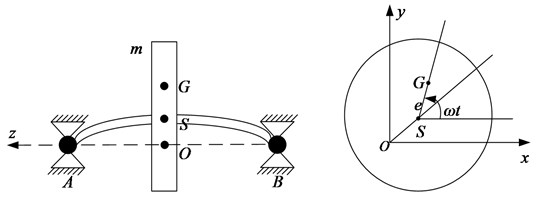
If the coordinate of $G$is $G(x_G,y_G)$and the coordinate of $S$ is$\mathrm{}S(x,y)$, the coordinate of $G$ can be obtained:

According to the motion law of the disk, the differential equations of motion can be given:

By taking the Eq. (1) into the Eq. (2), it can be calculated:

Because the motion differential equation of the $x$ axis is similar to that of the $y$ axis, the motion of the $y$ axis is taken as the research object. Now the active balancing force provided by the actuator is added to rotor system and balancing force with time-delay$\mathrm{}\tau$, active balancing force is added to rotor motion equation, the differential equation of motion can be induced:

After transformation, it can be obtained:

In the equation above, $p=me$ is the original unbalance, $u$ is the corrected unbalance. Using the differential operator $s$, it is written as the form of the transfer function:

In the Eq. (6), ${\omega }_n=\sqrt{\frac{k}{m}}\mathrm{}$ is natural frequency, and $\epsilon =\sqrt{\frac{c}{4mk}}\mathrm{}$ is damping ratio of system.

3. Design of active balancing control method

Smith predictive control method is widely applied to the control of time-delay system. The basic principle is to estimate the dynamic characteristics of the control system in advance [6]. System error caused by time-delay is compensated with the predictor so that the controller can work in advance. Control system model of the single neuron PID based on Smith predictor is shown in Fig. 2. $r$ is the expected vibration of rotor, $y\left(k\right)$ is the actual vibration of rotor, $e\left(k\right)$ is the difference between the expected vibration $r$ and the actual vibration$y\left(k\right)$, $e_m\left(k\right)$ is the difference between the actual vibration of rotor and reference model output, $r_m\left(k\right)$ is the expected vibration of the corrected rotor, $x_m\left(k\right)$ is the output of Smith predictor without time-delay, $G_0\left(s\right)=\frac{1}{m\left(s^2+2\epsilon {\omega }_n+{\omega }_n^2\right)}$ is the transfer function of actual system model, $G_m\left(s\right)$ is the transfer function of prediction model, $p$ is the input of the original unbalance, $\tau$ is the time-delay of controller. Due to the fact that $G_m\left(s\right)$ can not necessarily represent the system model exactly, the two feedback loops are designed to ensure that the control system achieve satisfactory accuracy.

Fig. 2System model of single neuron PID control based on Smith predictor

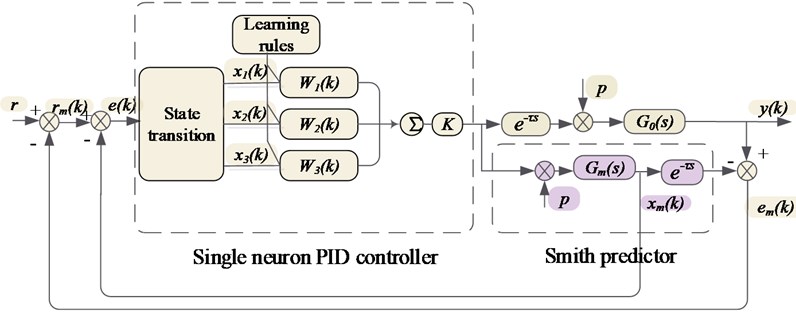
Because the traditional PID controller cannot adjust the control parameters, the single neuron PID control method is proposed based on the Smith predictor in the paper. The single neuron has the advantages of simple structure, simple calculation and fast learning speed [7].

The activation function of a single neuron network is linear. Therefore, the output of a single neuron is linearly related to the induced local region, the output of single neuron is obtained:

In the Eq. (8), $x_i\left(k\right)$ are 3 inputs of single neuron PID controller, the 3 inputs are as follows:

In the Eq. (8), $x_1\left(k\right)$ is the vibration error of the system at present, $x_2\left(k\right)$ is the change of the difference, and $x_3\left(k\right)$is the first order difference of the difference. For the weights $W_i\left(k\right)$ of single neuron controller, the improved supervised Hebb learning rule is proposed [8]:

In the Eq. (9), ${\eta }_i$ is the learning efficiency. Finally, the control law can be obtained:

4. Active balancing control algorithm

Based on the Smith predictor, the single neuron PID control algorithm is proposed in the paper. The process of the algorithm is shown in Table 1. The detailed steps are as follows:

1. The actual vibration $y\left(k\right)$ of the current rotor system is obtained by the vibration sensor and then the actual vibration is compared with the expected vibration$\mathrm{}r$. If $r<y\left(k\right)$, the balancing operation is performed, or the balancing operation is ended directly.

2. If the actual vibration $y\left(k\right)$ is greater than the expected vibration $r$, the amplitude difference $e\left(k\right)$ is calculated, and the three input signals of the controller $x_i\left(k\right)$ are calculated by amplitude difference$\mathrm{}e\left(k\right)$.

3. The weights $W_i\left(k\right)$ are calculated by three input signals of the controller $x_i\left(k\right)$, and finally the output $u\left(k\right)$ of the controller is obtained.

4. The controller controls the actuator to perform the balancing operation, and after the completion of balancing operation, the controller determines whether the actual vibration is less than the expected vibration. If $r>y\left(k\right)$, the balancing control process is finished; otherwise the operation will be repeated until the actual vibration is less than the expected vibration.

5. Experiment and analysis

The rotor system model is established and the control effect of this active balancing control method is verified by simulation based on MATLAB. It is assumed that the time-delay of the controller is known. The related parameters of flexible rotor system are as follows: the mass $m=$ 1 kg, the damping coefficient $c=$ 10 (Ns/m) and the stiffness of flexible rotor $K=$ 10⁶(N/m). The simulation model of flexible rotor system based on the proposed method is shown in Fig. 3.

Fig. 3Simulation model of the single neuron PID control method based on Smith predictor

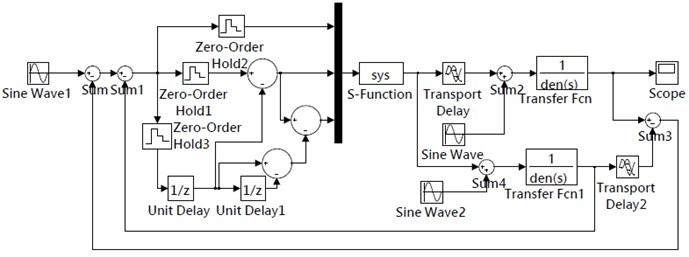
In order to verify the superiority of the proposed control method, traditional Smith predictive control method and the proposed method are validated under different time-delay conditions. The simulation results of two different control methods are shown in Fig. 4. Comparison of balancing time under different time-delay conditions is shown in Table 2.

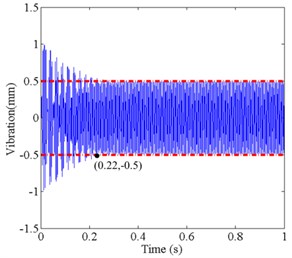
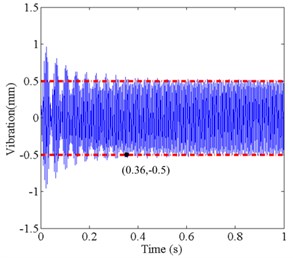
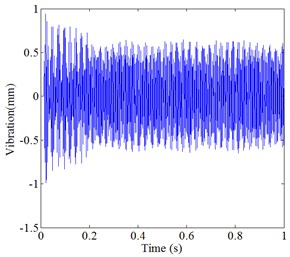
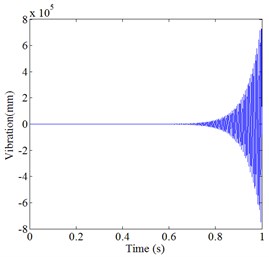
Fig. 4Simulation result of two control methods under different time-delay conditions: a) control result of single neuron PID based on Smith predictor at τ= 0.001 s, b) control result of traditional Smith predictor at τ= 0.001 s, c) control result of single neuron PID based on Smith predictor at τ= 0.01 s, d) control result of traditional Smith predictor at τ= 0.01 s

a)

b)

c)

d)

It can be seen from Fig. 4 and Table 2, the initial vibration of both methods is close to 1mm, when the time-delay is $\tau =$ 0.001 s. However, the balancing time of the proposed control method is 0.22 s, and the balancing time of traditional Smith predictive control method is 0.36 s. In large time-delay, the proposed control method still can achieve the expected vibration, while the traditional Smith control effect is not satisfactory, and it cannot reach the expected vibration.

6. Conclusions

In this paper, a single neuron PID control method based on Smith predictor is proposed for active balancing control of rotor with time-delay. The dynamics model of flexible rotor with time-delay is built by simplification, and then the Smith predictor of rotor system is constructed. The single neuron PID control method is designed to realize the active balancing control of rotor with time-delay. In order to verify the effectiveness of the proposed method, the simulation is carried out. When the time-delay is $\tau =$ 0.001 s, the proposed method has greatly reduced the control time compared with the traditional Smith control method, and what is more, this method is still applicable to the rotor system with large time-delay, while the traditional Smith control method cannot reach the expected vibration.