Axis current damage identification method based on bispectral locally preserving projection

1. Introduction

At present, the research on the shaft current is based on actual production, and summarizes the causes, hazards, and suppression measures of the shaft current [1-8]. Bispectral analysis can deal with non-stationary and non-Gaussian random series, and can theoretically completely suppress Gaussian noise. It has been widely used in the fault diagnosis of rotating machinery.

The manifold learning algorithm reveals the unique manifold structure of high-dimensional nonlinear data sets. [9-11]. Based on the above, this study uses bispectral local-preserving projection method to identify bearing shaft currents, performs envelope demodulation and bispectrum calculation of bearing vibration signals through Hilbert transform, and obtains bispectral amplitude eigenvector matrices. LPP reduces the dimensionality of the feature vector matrix to obtain low-dimensional fault features; finally, it uses support vector machines (SVM) to identify fault patterns. The experimental results show that this method can effectively identify bearing shaft current damage failure.

2. Rolling bearing vibration signal analysis

3. Bispectral local preserving projection algorithm

(1) Original vibration signal $x_{\left(t\right)}$, $x_{\left(t\right)}={\left[x_1,x_2,x_3,\cdots ,x_n\right]}^T$.

(2) The Hilbert transform is used to perform envelope demodulation on the vibration signals of different fault conditions.

Suppose signal $x_{\left(t\right)}=a_{\left(t\right)}\cos \left[2\pi f_s+{\phi }_t\right]$ among them $f_s$ is Carrier frequency, $a_{\left(t\right)}$ is the envelope of $x_{\left(t\right)}$, ${\phi }_t$ is the phase modulation signal of$x_{\left(t\right)}$. $a_{\left(t\right)}=1+\sum _{m=1}^M{x}_m\cos \left(2\pi f_{m}t+{\gamma }_m\right)$, $f_m$ is the frequency component of the modulation signal $a_{\left(t\right)}$, ${\gamma }_m$ is the initial phase angle of $f_m$. Analyze signal $Z_{t=}{e}^{j\left[2\pi f_s+{\phi }_t\right]}\left[1+\sum _{m=1}^M{x}_m\cos \left(2\pi f_{m}t+{\gamma }_m\right)\right]$.

(3) Bispectral estimation of demodulated signals. Fourier transform $x_{\left(f\right)}$ based on the vibration signal $x_{\left(t\right)}$. Modulated signal bispectrum:

where $X^{*}\left(f\right)$ is the conjugated number of $X\left(f\right)$, $E\left[\right]$ indicates mathematical expectation, $f_c$ is the carrier frequency, $f_x$ is the modulation frequency.

(4) Using LPP to reduce dimension of amplitude eigenvector matrix to obtain low-dimensional fault features.

Assume $n$$d$-dimensional high dimensional matrix samples $B_{ms}=\left[x_1,x_2,x_3,\dots ,x_n\right]$, a set of vector matrix $Y=\left[y_1,y_2,y_3,\dots ,y_n\right]$ is obtained by projection through a $d$-dimensional matrix $W$, among them $Y_j=W^t{x}_j$, $j=\mathrm{1,2},3,\dots ,n$.

The transformation matrix $W$ can be obtained by minimizing the following objective function:

where $W$ is the weight matrix, it can be defined with $K$ nearest neighbors:

where $x_i$ is the nearest neighbor of $x_j$.

After the dimensionality reduction, the feature space can maintain the local structure of the original high-dimensional space:

Mapping function $W=\left[w_1,w_2,w_3,\dots ,w_n\right]$.

(5) Input the corresponding low-dimensional fault features of the test sample into the trained classifier SVM to identify the test sample fault status.

4. Wind turbine bearing shaft current damage identification

4.1. Experimental data

The simulation test bench for bearing axis current damage is shown in Fig. 2(a). The test bearing used in this experiment is a detachable deep groove ball bearing. The test stand includes 1 motor; 2 insulating joints; 3 main shafts; 4 support bearing seats; 5 carbon brushes; 6 test bearing housings; 7 vibration acceleration sensor; 8 insulated bearings; 9 base; 10 adjustable DC switching power supply.

Fig. 1Bearing shaft current damage test bench

Through the experiment, the outer ring fault bearing with axial current damage is obtained. Then, the outer ring pitting failure and inner ring pitting failure of the bearing are obtained by electric spark. The acquisition system of this experiment is a B&K acquisition system. The bearing model is 6205EKA. Its bearing parameters and characteristic frequency under the corresponding rotating speed are shown in Table 1. Bearings in different states are shown in Fig. 2.

Table 16205EKA deep groove ball bearing related parameters

Name	Numerical value
Bearing outer diameter / mm	52
Bearing inner diameter / mm	25
Bearing width / mm	15
Rolling body diameter / mm	7.925
Bearing pitch diameter / mm	39
Number of rolling bodies	9
Contact angle	0
Outer ring fault characteristic frequency / Hz	71.7
Inner ring fault characteristic frequency / Hz	108.3

Fig. 2Bearings in different states

a) Normal status

b) Axis current outer ring failure

c) Pitting outer ring failure

d) Pitting inner ring failure

4.2. Fault feature extraction

The function parameters of this experiment were set as follows: transform length, window function selection, number of estimated samples, percentage of overlap. The bispectrum of different bearing states are shown in Fig. 3, respectively.

It can be seen from Fig. 3 that the characteristic frequency of the bearing fault under different conditions, but it is difficult to distinguish the axial current outer ring fault and the pitting outer ring fault from the figure. However, after the bispectral estimation, the amplitude eigenvectors of different fault states are obtained and the fault feature extraction is preliminarily completed. The fault feature extraction and recognition effect of LPP algorithm fault feature extraction and bispectral local-preserving projection method is shown in Fig. 4.

It can be seen from Fig. 4 that the LPP method has a good ability to aggregate faults. The bispectral locally-preserving projection method can well identify bearing faults.

Fig. 3Bispectrum of different bearing states

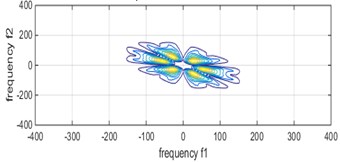
a) Normal status

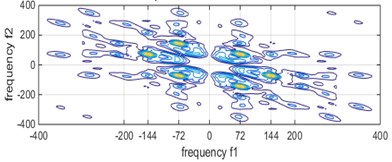
b) Axis current outer ring failure

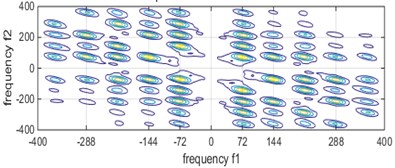
c) Pitting outer ring failure

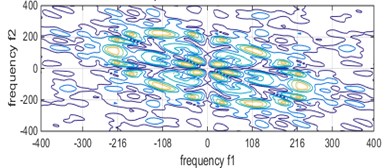
d) Pitting inner ring failure

Fig. 4Fault feature extraction and recognition effect of LPP algorithm and bispectral local-preserving projection

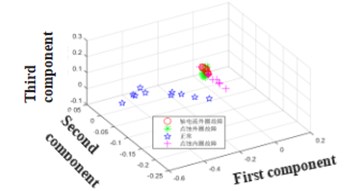
a) LPP

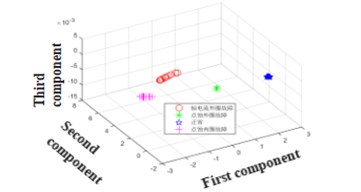
b) Bispectral localized projection

5. Conclusions

Aiming at the problem that the fault bearing vibration signal of bearing shaft current in wind turbine is complex and it is difficult to extract effective fault features, a fault identification method based on bispectral locality-preserving projection is proposed. In this method, the bispectrum can effectively represent the running state information of the rolling bearing and has obvious differences in different fault types. The vibration signal of the bearing is envelope-spectrum-demodulated and bispectrum-estimated to obtain the amplitude eigenvector matrix. Due to the large dimension of the bispectral amplitude eigenvector matrix, the bispectral amplitude eigenvector matrix is reduced by the locality-preserving projection algorithm. The bispectrum is projected to the eigendimensional space under the condition that the bispectral local structure is invariable, and the low dimensional fault features of the bearing are obtained. The low dimensional feature vector is input into the SVM classifier to identify and judge the bearing fault. The experimental results show that the proposed method can effectively identify bearing shaft current damage faults, and the classification accuracy of bearing faults containing shaft current damage can reach 96.25 %.